獨立成分分析（Independent Component Analysis，ICA）是一種統計與計算技術，主要用于信號分離，即從多種混合信號中提取出獨立的信號源。ICA在處理盲源分離（Blind Source Separation，BSS）問題時尤為有效，如從錄音中分離出不同的聲音源、從腦電圖（EEG）中提取出獨立的神經活動信號等。

ICA的基本原理

ICA假設觀察到的信號是若干獨立信號源線性混合的結果。目標是從這些觀察到的信號中恢復出原始的獨立信號源。

假設有

個觀測信號，這些信號是由 個獨立信號源通過一個未知的線性混合矩陣線性組合得到的，即：

ICA的目標是找到一個解混合矩陣

，使得：

其中

是估計的獨立成分向量，盡可能接近原始的獨立信號源。

ICA的假設條件

1. 獨立性假設：信號源彼此之間相互獨立。

2. 非高斯性假設：獨立成分（信號源）遵循非高斯分布。這一假設是ICA區分獨立成分的關鍵。

主要算法

ICA有多種實現算法，其中比較常用的包括：

1. FastICA：一種迭代算法，通過最大化非高斯性（如負熵）來估計獨立成分。

2. Infomax ICA：基于最大化信息傳輸的算法，通過最大化信號的熵來實現信號分離。

3. **JADE (Joint Approximate Diagonalization of Eigen-matrices)**：基于四階累積量矩陣的聯合近似對角化來分離獨立成分。

應用領域

1. 生物醫學信號處理：如腦電圖（EEG）、心電圖（ECG）信號的分離和分析。

2. 語音信號處理：從混合錄音中分離出不同的語音源。

3. 圖像處理：在圖像去噪、特征提取等方面應用廣泛。

4. 金融數據分析：用于分離和識別金融時間序列中的獨立成分。

優點與局限性

優點：

1. 能夠有效地分離出相互獨立的信號源。

2. 適用于各種信號處理領域，應用廣泛。

局限性：

1. 對混合矩陣的精確估計要求較高。

2. 對信號源的獨立性和非高斯性有較強的假設，實際應用中可能不完全滿足。

3. 算法復雜度較高，計算量大。

實例

以下是使用Python庫Scikit-learn進行ICA分析的一個簡單示例：

import?numpy?as?np
import?matplotlib.pyplot?as?plt
from?sklearn.decomposition?import?FastICA#?生成混合信號
np.random.seed(0)
time?=?np.linspace(0,?1,?200)
S1?=?np.sin(2?*?np.pi?*?1?*?time)??#?正弦波
S2?=?np.sign(np.sin(3?*?np.pi?*?2?*?time))??#?方波
S?=?np.c_[S1,?S2]
S?+=?0.1?*?np.random.normal(size=S.shape)??#?添加噪聲#?混合信號
A?=?np.array([[1,?1],?[0.5,?2]])??#?混合矩陣
X?=?np.dot(S,?A.T)??#?觀測信號#?使用FastICA進行獨立成分分析
ica?=?FastICA(n_components=2)
S_?=?ica.fit_transform(X)??#?估計的信號源
A_?=?ica.mixing_??#?估計的混合矩陣#?繪制信號
plt.figure(figsize=(10,?8))plt.subplot(3,?1,?1)
plt.title("Original?Signals")
plt.plot(time,?S[:,?0],?label='Signal?1')
plt.plot(time,?S[:,?1],?label='Signal?2')
plt.legend()plt.subplot(3,?1,?2)
plt.title("Mixed?Signals")
plt.plot(time,?X[:,?0],?label='Mixed?Signal?1')
plt.plot(time,?X[:,?1],?label='Mixed?Signal?2')
plt.legend()plt.subplot(3,?1,?3)
plt.title("ICA?Recovered?Signals")
plt.plot(time,?S_[:,?0],?label='Recovered?Signal?1')
plt.plot(time,?S_[:,?1],?label='Recovered?Signal?2')
plt.legend()plt.tight_layout()
plt.show()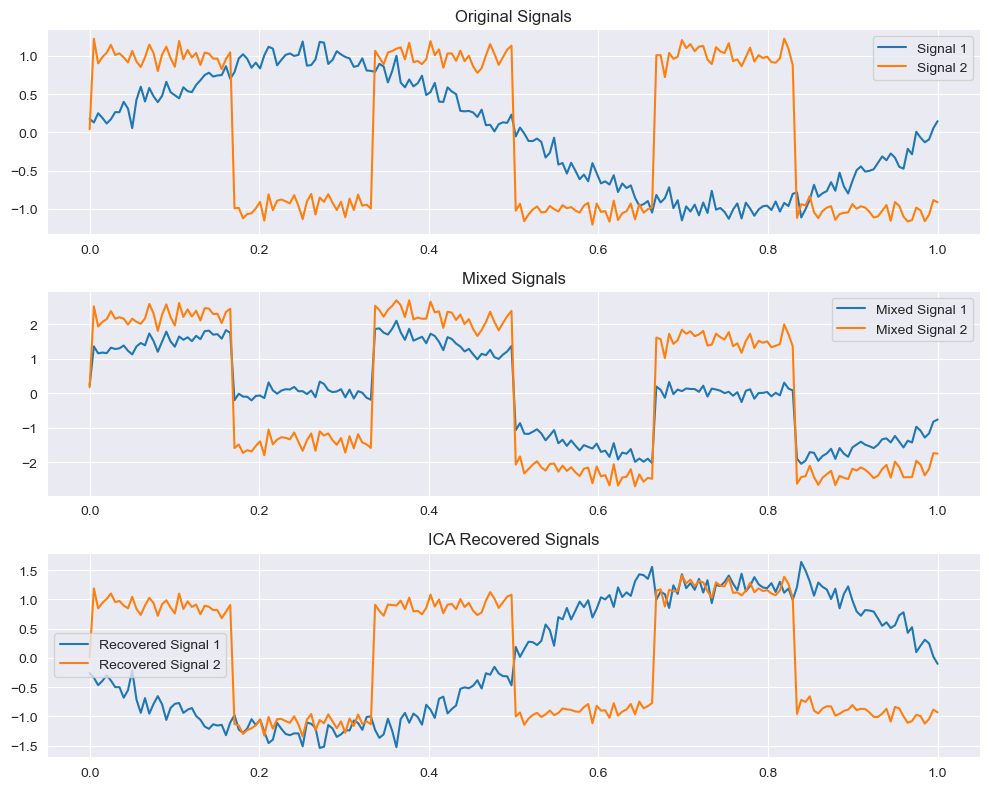

這段代碼將生成三個子圖：

1. 原始信號：顯示最初生成的兩個獨立信號（一個正弦波和一個方波）。

2. 混合信號：顯示通過混合矩陣生成的兩個觀測信號。

3. 分離出的信號：顯示通過ICA分離出的信號，它們應該與原始信號非常相似。

其中：

• 原始信號顯示了生成的兩個獨立信號。

• 混合信號展示了線性組合后的混合信號。

• 分離出的信號是通過ICA算法分離出的兩個獨立信號，它們應盡可能接近原始信號。

通過上述代碼，可以將混合信號分離成獨立的信號源，從而實現信號分離的目的。

我們繼續使用網上公開的音樂文件對其進行混合處理后，再使用FastICA進行獨立成分分析。

原始音頻：

music1（SalmonLikeTheFish - Glacier）：

music2（Aitua - Johann Pachelbel - Kanon in D Dur）：

由于設置采樣按照最短的音頻文件進行采樣，因此混合后的音頻和最終獨立成分分析之后的音頻都只是3：21的長度。

ICA獨立成分分析處理：

import?os
import?numpy?as?np
import?matplotlib.pyplot?as?plt
import?librosa
import?soundfile?as?sf
from?sklearn.decomposition?import?FastICA#?設置音頻文件目錄
audio_dir?=?'MusicMix'
music1_path?=?os.path.join(audio_dir,?'music1.wav')
music2_path?=?os.path.join(audio_dir,?'music2.wav')#?檢查音頻文件是否存在
if?not?os.path.exists(music1_path)?or?not?os.path.exists(music2_path):raise?FileNotFoundError("請確保所有音頻文件已下載并放置在正確的目錄中。")#?加載音頻文件
music1,?sr1?=?librosa.load(music1_path,?sr=None)
music2,?sr2?=?librosa.load(music2_path,?sr=None)#?確保采樣率相同
if?sr1?!=?sr2:raise?ValueError("兩個音頻文件的采樣率不同。")#?使兩個音頻文件具有相同的長度
min_len?=?min(len(music1),?len(music2))
music1?=?music1[:min_len]
music2?=?music2[:min_len]#?創建混合信號
mix1?=?music1?+??music2
mix2?=?0.5?*?music1?+?music2#?創建混合信號矩陣
X?=?np.c_[mix1,?mix2]#?使用FastICA進行獨立成分分析
ica?=?FastICA(n_components=2,?max_iter=1000,?tol=0.001)
S_?=?ica.fit_transform(X)??#?估計的信號源
A_?=?ica.mixing_??#?估計的混合矩陣#?繪制信號
time?=?np.arange(len(mix1))?/?sr1plt.figure(figsize=(10,?8))plt.subplot(3,?1,?1)
plt.title("Original?Music?Signals")
plt.plot(time,?music1,?label='Music?1')
plt.plot(time,?music2,?label='Music?2')
plt.legend()plt.subplot(3,?1,?2)
plt.title("Mixed?Music?Signals")
plt.plot(time,?mix1,?label='Mixed?Signal?1')
plt.plot(time,?mix2,?label='Mixed?Signal?2')
plt.legend()plt.subplot(3,?1,?3)
plt.title("ICA?Recovered?Music?Signals")
plt.plot(time,?S_[:,?0],?label='Recovered?Signal?1')
plt.plot(time,?S_[:,?1],?label='Recovered?Signal?2')
plt.legend()plt.tight_layout()
plt.show()#?保存混合后的音頻信號
sf.write(os.path.join(audio_dir,?'mixed1.wav'),?mix1,?sr1)
sf.write(os.path.join(audio_dir,?'mixed2.wav'),?mix2,?sr1)#?保存分離后的音頻信號
sf.write(os.path.join(audio_dir,?'recovered1.wav'),?S_[:,?0],?sr1)
sf.write(os.path.join(audio_dir,?'recovered2.wav'),?S_[:,?1],?sr1)

波形圖輸出：

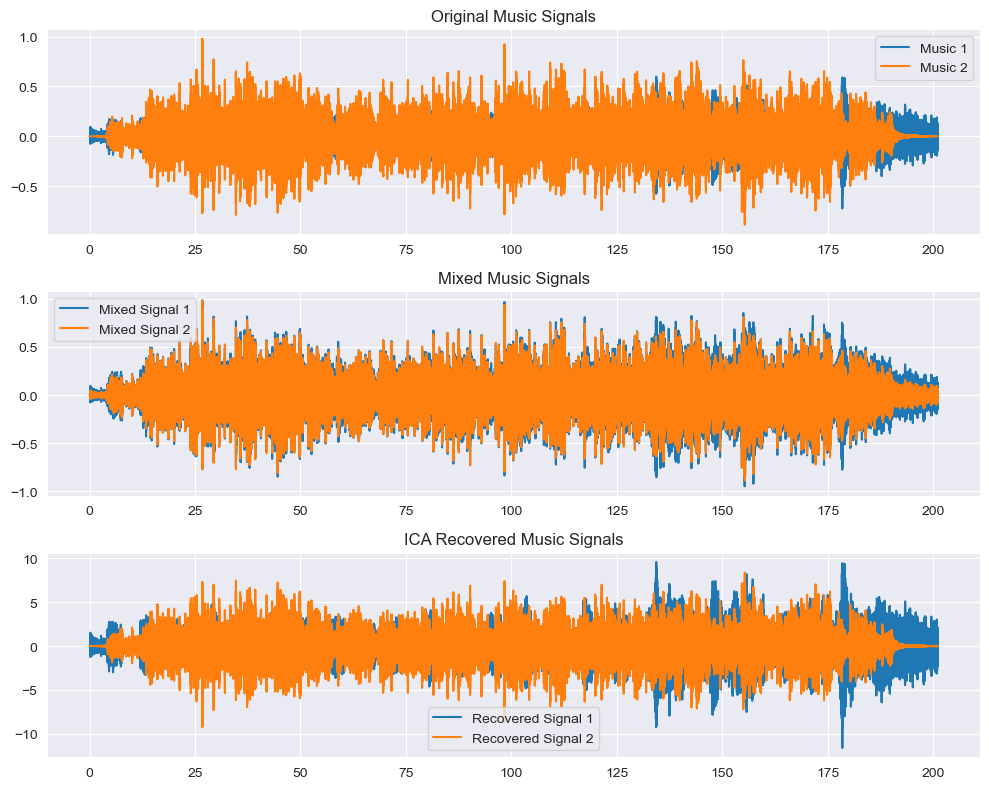
重新分離出的兩段音樂：

從以上兩個音頻的輸出可知，ICA成功分離出了兩手不同的歌曲，雖然音質回有部分損失。我們實現了將兩個音樂信號混合，并使用ICA技術將它們分離回原始的獨立信號。關鍵步驟包括確保采樣率一致、對齊音頻長度、創建混合信號以及應用ICA算法。結果顯示在圖表中，并保存為音頻文件供進一步分析和使用。這一過程展示了ICA在信號處理中的強大應用，特別是對于混合音頻信號的分離。

以上內容總結自網絡，如有幫助歡迎轉發，我們下次再見！