鋰電池一階模型-在線參數辨識
- 背景
- 在線 VS 離線 參數辨識
- 遞推最小二乘法
- 一階戴維南Z域離散表達式
背景
鋰電池一階戴維南等效模型的基礎知識和離線辨識方法,已經在上一期非常詳細地講解了一輪(上期文章請戳此處),本期繼續講解一下如何進行在線辨識。
此篇推文繼續使用論文《基于RLS方法的磷酸鐵鋰電池模型辨識及SOC估計策略研究》中的方法,作者為西南交通大學-鄭衛同學;用到的模型在上一期可以獲取。
在線 VS 離線 參數辨識
- 首先,我們來詳細說說在線辨識與離線辨識的基礎概念。
兩者本質的區別為,辨識的過程是否在系統正常運行過程中實時或周期性地估計參數。
離線辨識是在系統不運行或實驗條件下進行的參數估計過程。它通常涉及收集系統的靜態或歷史數據,然后通過復雜的計算和數據分析來確定模型參數。離線辨識的優勢在于能夠使用更復雜的算法和模型,因為它不受實時性約束,可以花更多的時間和計算資源來提高辨識精度。這種方法常用于研發階段,幫助工程師理解系統的工作原理,優化設計,或建立精確的模型用于仿真。
在線辨識是在系統正常運行過程中實時或周期性地估計參數的技術。它通過實時監測系統的輸入輸出信號(如電流、電壓、速度等),使用快速算法實時更新模型參數,以適應系統隨時間和環境變化的動態特性。在線辨識強調實時性和魯棒性,適合需要動態調整控制策略的應用場景。
- 其次我們想一想,為什么需要在線辨識?
鋰電池特性的影響因素很多,如焊接工藝,溫度,電流倍率和電池本身的劣化等。上述在線辨識的基本概念,已經體現了它的優勢-可以適應系統隨時間和環境變化的動態特性。因此,純粹通過離線辨識多個參數組,不僅耗費大量時間和金錢,而且在實際使用中會因為單個或者多個因素疊加,導致離線參數實用性差,從而導致模型算法難以精準表征電池狀態。 - 那是不是離線辨識就沒有意義了?
并不是。通過離線辨識,我們可以提前知道該電池參數的大致范圍,可以用于在線辨識開始前的參數初始化以及在線辨識結果的上下限判斷。
遞推最小二乘法
論文中在線辨識的方法為帶遺忘因子的遞推最小二乘法,以下內容摘自論文
對電池系統而言,根據系統辨識的理論建立數學模型,利用實驗的輸入輸出數據 辨識所需要的參數,就是電池模型的參數辨識。本文選用遞推最小二乘法(Recursive Least Squares Method,RLS)進行模型的參數辨識。遞推最小二乘法是一種線性無偏估算方法,使觀測誤差的平方和達到極小,主要特點是適用性非常廣,線性系統和非線性系統均適用;動態系統和靜態系統也均適用;離線估算和在線估算均可用該方法;在隨機環境下,觀測得到的數據即使沒有相關的概率統計信息,使用遞推最小二乘法 的估算結果仍具有良好的統計特性。
遞推最小二乘法(RLS)是在最小二乘法(LS)的基礎上發展來的一種估算方法,是對一次最小二乘法的估算值修正后的一種在線辨識方法。當辨識系統啟動后,每取得一次新的觀測數據,就在前一次估算結果的基礎上,引入此次新的觀測數據對前一次估算的結果作修正,進而遞推得出新的參數估值。如此算法進行下去,隨著新的觀測數據不斷被引入進來,就實現了一次接一次的參數辨識,參數估算值直至收斂到合格精度為止。
遞推最小二乘法的基本思想:新估算值=舊估算值+修正項 基本計算公式為:
RLS方法具有無限記憶長度,隨著遞推運算過程的不斷進行,舊的數據越來越多導致出現數據飽和的現象,使得遞推結果逐漸失效。因此為避免這種情況,引入遺忘因子,當時,就退變為普通的遞推最小二乘法,越小表示遺忘速度越快,跟
蹤能力越強,但波動也越大,一般取[0.95 1]。
這里需要說明一點,遞推最小二乘法本身沒有在線或者離線屬性,取決于我們實際如何用它。你把它放在的嵌入式代碼中跑,每新采集一組數據時算一次,就成了在線辨識;你已經有了數據,再去按步驟遞推就是離線辨識。
一階戴維南Z域離散表達式
在使用遞推前,首先要推導出參數矩陣與數據矩陣的離散關系式。
基礎表達式還是下面這個,只不過咱們需要對它進行離散化。
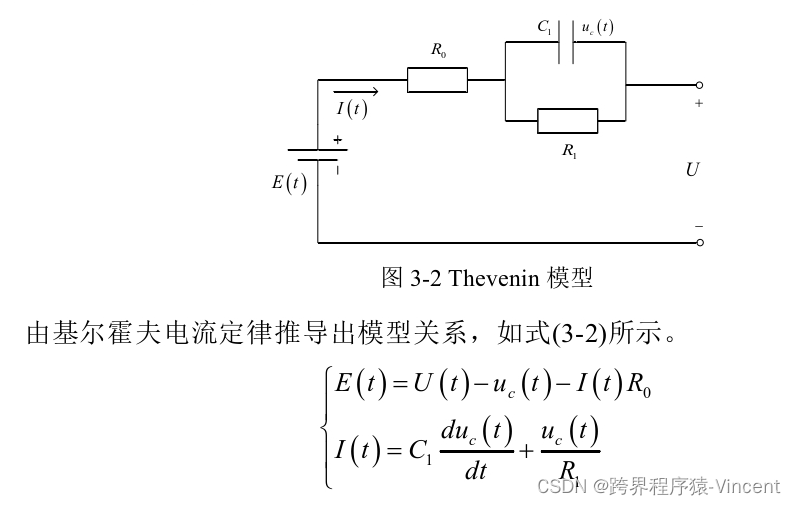

注:這里面涉及到一個電流哪個方向為正方向問題,論文此處兩個筆誤,以免誤導:
- 上圖的uc(s)與uc(t)是兩個概念,不是同一個,但為了和論文統一,我接下來的uc統一指的是內部壓降,而非電容的電壓
- 若以放電方向為正方向,則uc = E(k) - V(k) ,其中V(k)為端電壓,即實際采集到的電池電壓,所以論文中的式子3-2是錯誤的
但是這個式子怎么來的呢?對于沒有學過信號處理或者控制理論的人來說,在看類似論文時,會一頭霧水。如果只想應用結論的,則可以跳開此部分內容,直接看本章最后的內容。
在s域分析中,電阻和電容并聯的等效阻抗可以用復頻域的運算來表示。在時域中,電阻的阻抗是純實數,而電容的阻抗是純虛數并且與頻率有關。將它們轉換到s域(拉普拉斯變換的領域),電阻R的阻抗仍然是R(因為其即時響應特性),而電容C的阻抗變為1/cs.
因此,電阻R與電容C并聯的總阻抗Z可以用以下公式表示:
Z = 1 1 R + 1 1 s C Z = \frac{1}{\frac{1}{R} + \frac{1}{\frac{1}{sC}}} Z=R1?+sC1?1?1?
簡化后得到:
Z = R ? 1 s C R + 1 s C Z = \frac{R \cdot \frac{1}{sC}}{R + \frac{1}{sC}} Z=R+sC1?R?sC1??
Z = R 1 + R s C = R 1 + τ s Z = \frac{R}{1 + RsC}= \frac{R}{1 + τs} Z=1+RsCR?=1+τsR?
傳遞函數一般都會寫成 輸出/輸入 的形式,因此再加上R0與R1C1串聯,則可以得到上述s域的表達式。
但是s域主要應用于連續時間信號和系統的分析,要放在遞推中,還需要轉為z域形式。z域是通過Z變換(Z Transform)從離散時間域轉換而來,其中z也是一個復數變量,主要關注的是離散時間序列的頻域特性。z變換適用于數字信號處理、數字控制以及任何涉及采樣數據系統的分析,比如數字濾波器設計、數字信號處理器(DSP)算法開發等。
從s域轉到z域,通常使用雙線性變換,即通過下述方法,將s替換。
s = 2 T ? 1 ? z ? 1 1 + z ? 1 或 2 T ? z ? 1 z + 1 s= \frac{2}{T}*\frac{1-z^-1}{1+z^-1}或 \frac{2}{T}*\frac{z-1}{z+1} s=T2??1+z?11?z?1?或T2??z+1z?1?
兩者是等效的,前者是后者分子分母同時除了z而已,其中T為數據采樣周期。則最終可以得到形如這樣的標準的z域傳遞函數形式:

具體推導過程可以自行再推一次,下圖僅供參考。需要注明一點的是Z^-1乘上I(k)表示I(k)前一個采樣周期的值,即為遞推過程的I(k-1)值。
最終得到的:
a 0 = T + 2 ? τ = T + 2 ? R 1 ? C 1 a0=T+2*τ=T + 2*R1*C1 a0=T+2?τ=T+2?R1?C1
a 1 = T ? 2 ? τ = T ? 2 ? R 1 ? C 1 a1=T-2*τ=T-2*R1*C1 a1=T?2?τ=T?2?R1?C1
b 0 = T ? ( R 0 + R 1 ) + 2 ? R 0 ? τ b0=T*(R0+R1)+2*R0*τ b0=T?(R0+R1)+2?R0?τ
b 1 = T ? ( R 0 + R 1 ) ? 2 ? R 0 ? τ b1=T*(R0+R1)-2*R0*τ b1=T?(R0+R1)?2?R0?τ
再令
c 1 = ? a 1 a 0 c1=-\frac{a1}{a0} c1=?a0a1? c 2 = b 0 a 0 c2=\frac{b0}{a0} c2=a0b0? c 3 = b 1 a 0 c3=\frac{b1}{a0} c3=a0b1?
可得
U c ( k ) = c 1 ? U c ( k ? 1 ) + c 2 ? I ( k ) + c 3 ? I ( k ? 1 ) Uc(k) = c1*Uc(k-1) + c2*I(k) + c3*I(k-1) Uc(k)=c1?Uc(k?1)+c2?I(k)+c3?I(k?1)

注:上圖推導過程將c1的符號位忘了移到Uc(k-1)側了,懶得重新寫了
由c1,c2,c3,我們可以逆推R0,R1,C1的表達式

回到剛才的遞推最小二乘法表達式,采用矩陣的方式進行表達

論文部分符號的含義沒有解釋清楚,在此一并補充說明:
- K-增益矩陣,影響了新數據對參數估計的影響程度。可以不用給初值,每次迭代過程中產生
- P-協方差矩陣,需要根據實際情況給定初值。其對角線上的元素表示各個參數估計值的不確定性的平方,這其實就是協方差的定義。初值的選擇會影響算法的收斂速度和參數估計的準確性。一般來說,初值越大,說明預設的參數與真實參數的偏差比較大,則算法在初始階段對觀測數據的響應越靈敏,但也可能導致算法在收斂過程中出現較大的波動。
- z(t) - 有些文獻寫的是y(k),離散化表達式的左值,對應于我們的模型就是Uc(k)觀測值=電池端電壓-當前SOC態下Uoc
則根據前面的推導,套入到RLS遞推,有如下表達式
θ = [ c 1 c 2 c 3 ] \theta=[c1\ c2\ c3] θ=[c1?c2?c3] ? = [ ? U c ( k ? 1 ) I ( k ) I ( k ? 1 ) ] T \phi=[-Uc(k-1)\ I(k)\ I(k-1)]^T ?=[?Uc(k?1)?I(k)?I(k?1)]T
接下來就會用到我們上一篇離線參數辨識的結果了。而且我們需要給協方差矩陣P一個初值,我們認為經過了離線辨識,參數已經比較準了,可以給個對角元素均為1的3*3矩陣,同時根據表達式,可以給出c1-c3的初值。代碼如下:
% 執行該腳本前,請確認simulink模型與該腳本文件是否在同一路徑clear all; % 清除工作區中的所有變量
close all; % 關閉所有已打開的圖形窗口
clc; % 清空命令窗口的內容% 打印腳本開始的信息(可選)
fprintf('Script started.\n');% 這里開始編寫你的MATLAB腳本內容...% 步驟1: 運行模型,并提取所需數據用于其他步驟(模型的數據已經通過設置,輸入到工作區)
% 具體方法為用Scope記錄模型仿真過程數據,然后配置為輸出到工作區
modelname = 'Battery.slx';
sim(modelname);% 步驟2: 根據之前離線辨識的結果,確定參數給定初值,注意:遞推用的是c1-c3
% 獲取模型的運行步長,用于遞推的輸入,因為我們的模型是定步長.,所以可以用如下接口獲取
T = 0.1;%str2double(get_param('Battery.slx', 'FixedStep'));
R1C1_init = 7154.10;
R0_init = 0.001661;
C1_init = 4306554.1;
R1_init = R1C1_init / C1_init;c1_init = (T - 2 * R1C1_init) / (T + 2 * R1C1_init);
c2_init = ((R0_init + R1_init) * T + 2 * R1C1_init) / (T + 2 * R1C1_init);
c3_init = ((R0_init + R1_init) * T - 2 * R1C1_init) / (T + 2 * R1C1_init);theta = [c1_init c2_init c3_init]'; %參數向量初值
phi = zeros(1, 3); %數據向量初值
P = 1*eye(3); %協方差矩陣
K = zeros(3,1); %增益矩陣
lambda = 0.99;% 步驟3: 遞推
% 數據準備
Ut = ScopeData4.signals(2).values; % Scope中的數據索引似乎從1開始
Ibat = ScopeData4.signals(3).values;
Soc = ScopeData4.signals(1).values;
time_val = ScopeData4.time;% 見博客說明,先處理z(k) = Ut(k) - Uocv(k)
% 基于SOC獲取OCV -- 見論文的擬合公式
ocv = -95.82*Soc.^8 + 549.26*Soc.^7 ...-1219.4*Soc.^6 + 1387.01*Soc.^5 ...-883.38*Soc.^4 + 320.4*Soc.^3 ...-64.45*Soc.^2 + 6.89*Soc + 2.91;
Uc = Ut - ocv;
R0 = zeros(1, size(Uc, 1) - 1);
R1 = zeros(1, size(Uc, 1) - 1);
C1 = zeros(1, size(Uc, 1) - 1);% 遞推主體
for i = 2 : size(Uc, 1)Phi = [-Uc(i - 1) Ibat(i) Ibat(i - 1)];K = P * Phi' / (Phi * P * Phi' + lambda);theta = theta + K * (Uc(i) - Phi * theta);P = (eye(3) - K*Phi) * P / lambda;% 基于遞推結果,反推R0, R1, C1c1_k = theta(1);c2_k = theta(2);c3_k = theta(3);R0(i) = (c2_k - c3_k)/(1 - c1_k);R1(i) = (c2_k + c3_k) / (1 + c1_k) - R0(i);C1(i) = T * (1 - c1_k) / (2 * R1(i) * (1 + c1_k));
end% 步驟4: 畫圖查看遞推過程情況圖
figure;
subplot(2,2,1); % 創建一個2行2列的子圖,并激活第1個子圖
plot(time_val, Ut, 'o', 'MarkerFaceColor', 'g', 'MarkerEdgeColor', 'k', 'LineWidth', 1, 'DisplayName', '電壓曲線');
title('原始曲線');
hold on;
plot(time_val, Ibat, 'r-', 'LineWidth', 1, 'DisplayName', '電流曲線');
legend('show');
xlabel('Time (s)');
ylabel('Voltage/Current');
hold off; % 關閉保持狀態,避免下一個子圖影響當前子圖subplot(2,2,2); % 激活第2個子圖,顯示R0
plot(time_val, R0 * 1000, 'bx', 'MarkerFaceColor', 'b', 'LineWidth', 1, 'DisplayName', 'R0');
legend('show');
xlabel('Time (s)');
ylabel('R0(mO)');
title('R0-遞推');
hold off; % 關閉保持狀態,避免下一個子圖影響當前子圖subplot(2,2,3); % 激活第3個子圖,顯示R1
plot(time_val, R1 * 1000, 'bx', 'MarkerFaceColor', 'b', 'LineWidth', 1, 'DisplayName', 'R1');
legend('show');
xlabel('Time (s)');
ylabel('R1(mO)');
title('R1-遞推');
hold off; % 關閉保持狀態,避免下一個子圖影響當前子圖subplot(2,2,4); % 激活第4個子圖,顯示R0
plot(time_val, C1, 'bx', 'MarkerFaceColor', 'b', 'LineWidth', 1, 'DisplayName', 'C0');
legend('show');
xlabel('Time (s)');
ylabel('C1');
title('C1-遞推');
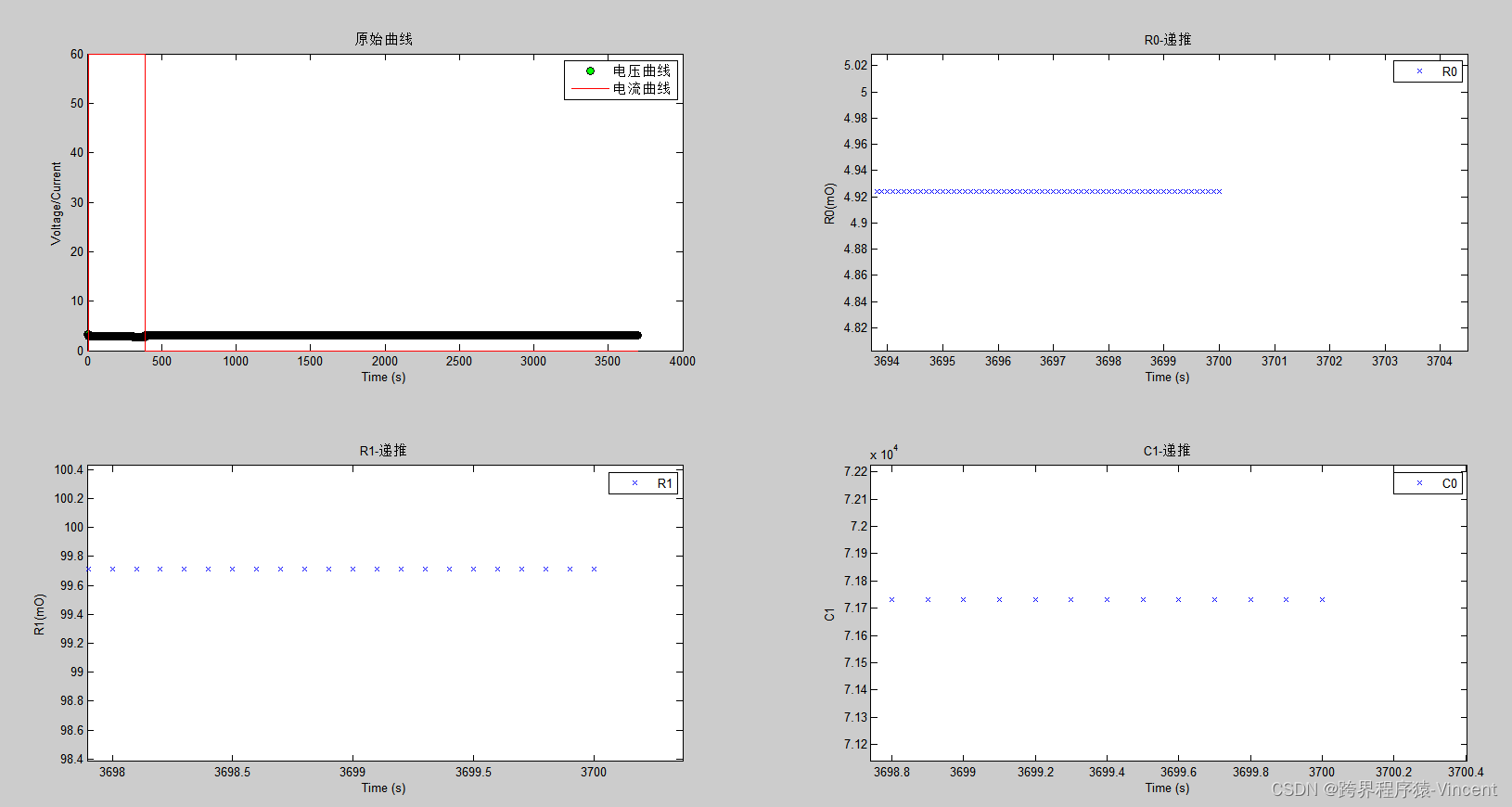
R0= 0.0049, R1 =0.0997, C1 =7.1732e+04
最終辨識結果如上

)




)

)

)

——controller方法參數與html表單對應)




方法)


