概論

在第一部分中，我們深入探討了人工智能的興衰簡史以及推動人工智能發展的努力。我們研究了一個簡單的感知器，以了解其組件以及簡單的 ANN 如何處理數據和權重層。在簡單的 ANN 中，不會對數據執行特定操作。ANN 中的激活函數是一個線性函數，它將輸入數據帶到輸出，因此它與傳統模型中的回歸任務沒有太大區別。

但是，如果我們想要處理更大的數據集并實現諸如人臉識別或自然語言處理之類的結果，那么僅使用線性激活函數是不切實際的，因為它不執行特定的操作。在所有非線性激活函數中，哪一個表現最佳？激活函數存在哪些問題，我們如何才能最小化這些問題？信息在神經元中是如何處理？順序處理還是并行處理更好？我們可以將它們結合起來嗎？神經元必須能夠學習。但是我們有哪些類型的學習？數據可能是帶標簽的，也可能是未帶標簽的，就像我們在傳統的機器學習模型中一樣。當神經網絡中的層數增加并且我們深入研究時，這是如何做到的？反向傳播如何工作？它可能存在哪些問題，我們如何才能最小化這些問題？鏈式法則！？讓我們一起打開大門，深入研究它……

人工神經網絡如何學習？

了解所有生物體的學習過程一直是人類感興趣的課題。甚至人類學習自己的方式也是如此。人類大腦可以并行處理信息并同時執行多項活動，這意味著它可以同時分析不同的信息。然而，一些心理活動需要順序處理來解決更復雜的問題，這些問題需要更詳細的分析和理解。當然，這個過程究竟如何在大腦中進行，仍然是科學家和神經科學家的研究課題。

在人工神經網絡中，我們可以根據問題的類型來確定架構和學習的類型。例如，在自然語言處理 (NLP) 中，數據具有特定的順序，循環神經網絡 (RNN) 被廣泛使用，其中的信息處理是按順序進行的。每個輸入數據都按特定順序輸入網絡。當它們到達網絡的每一層時，對每個輸入執行各種處理（我們將在本文中進一步討論），然后生成與每個單詞或字符相關的輸出。

另一種處理類型是并行處理，它通常用于深度神經網絡 (DNN) 以提高速度和效率，因為它可以顯著減少任務執行時間。例如，在通常用于圖像處理的卷積神經網絡 (CNN) 中，會使用諸如三維圖像或大型矩陣之類的復雜操作。這些網絡廣泛使用并行處理進行矩陣操作，例如組合、分離和成像。這就是GPU（圖形處理單元）發揮作用的地方，因為 GPU 中的處理是并行完成的。這意味著多個計算操作可以同時并行執行。這允許同時執行數百萬個計算任務。

然而，在很多情況下，可以使用多種處理方法的組合。事實上，使用順序處理和并行處理的組合或在系統中使用不同的處理方法可以幫助提高性能和效率。這種方法被稱為混合處理。下面，我們將深入探討傳統方法和人工神經網絡中使用的機器學習方法類型。

神經網絡中的各種學習類型

在人工神經網絡的所有類型的學習中，目標都是讓網絡識別輸入數據中的模式并為新數據提供準確的預測。這些方法中的每一種都可以用于特定的任務。這些方法之一是監督學習，用于模式識別、分類、分類和預測等任務。在這種類型的學習中，網絡的輸入數據在訓練階段被標記。例如，在 ImageNet 數據集中，您已標記圖像以進行圖像處理，這使網絡能夠在訓練階段使用其擁有的標簽檢測模式并在測試階段獲得最佳結果。

下一種方法是無監督學習，通常用于發現隱藏模式、探索數據、聚類和分類數據。輸入數據在沒有標簽的情況下進行訓練。最好的例子是自動編碼器，旨在從未標記的數據中學習。主要目標是讓網絡重現數據的基本特征。自動編碼器是神經網絡中無監督學習的著名例子之一，目前被廣泛使用。

另一種方法是半監督學習，它可以被認為是監督學習和無監督學習的結合，因為它具有有限數量的標記數據以及豐富的未標記數據。這種類型的學習通常用于標記數據訪問有限但未標記數據豐富的情況。半監督學習的目標是同時使用標記數據和未標記數據來改進學習并提高模型準確性。例如，在醫學成像中，標記數據（例如，顯示特定疾病的圖像）可能有限。通過利用未標記數據，模型可以學習圖像中的重要結構。

強化學習用于計算機游戲、機器人技術和復雜的決策。在每個時間步驟中，代理都處于特定狀態，并根據其狀態（獎勵或懲罰）選擇特定操作。強化學習的主要目標是盡量減少懲罰并增加獎勵。代理會嘗試通過學習其在不同狀態下采取的操作與其從環境中獲得的獎勵或懲罰之間的關系來選擇最佳行為。

強化學習有多種算法，包括 Q 學習、深度 Q 網絡 (DQN)、策略梯度和 Actor-Critic。這些算法都基于類似的原理，但通過使用不同的技術和變體，它們可以解決不同的問題。強化學習的缺點之一是需要大量反復試驗才能學習，算法復雜，并且對參數調整敏感。

接下來，我們將深入研究激活的工作原理以及網絡的運作方式。請繼續關注這個無限美麗的探索。

1.激活函數

在 ANN 中，激活函數用于在層之間傳輸信息（從輸入到輸出，或者在循環模型中從輸出到輸入）。這些函數用于網絡的不同層以及從處理到加權、損失減少和最終結果的各個階段。本質上，這些函數導致神經元的整體行為變得非線性。

訓練深度網絡的主要挑戰之一是梯度消失問題，即當信息??從一層傳播到下一更高層時，梯度趨于接近于零。隨著訓練期間學習到的權重深入網絡，梯度通常趨于消失，導致網絡內的信息傳輸不足。這可能導致更深層中梯度的減少或消失。因此，使用適當的激活函數可以幫助緩解梯度消失問題并提高深度網絡的性能。

當然，激活函數的選擇取決于問題的類型和期望的結果。我們將討論各種類型的線性函數作為不同激活函數的示例。

線性激活函數

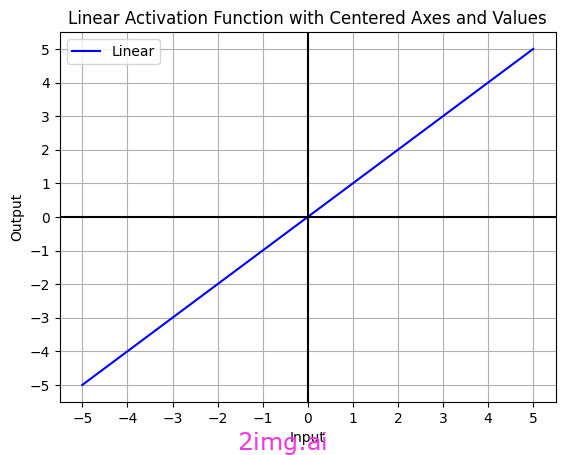
我使用 Python 代碼創建了線性激活函數。

線性激活函數，也稱為“恒等”或“無激活”函數，不執行任何輸入轉換。這些函數只是將輸入值不加修改地傳遞到輸出。它們通常用于特定情況和特殊問題。在某些情況下，例如回歸任務，它們可用于輸出層來計算預測值。

線性激活函數的公式為：

F(x) = x

線性激活函數有兩個主要缺點。首先，它們不能用于反向傳播；其次，它們會將神經網絡的所有層折疊成一層。換句話說，無論神經網絡有多少層，最后一層仍然是第一層的線性函數。這本質上將神經網絡變成了單層網絡。

在大多數模型中，非線性激活函數受到優先考慮，因為它們更適合解決復雜問題。

非線性激活函數

人工神經網絡 (ANN) 中激活函數的非線性使得它們能夠對復雜的關系進行建模。事實上，許多應用，尤其是當今世界，如人臉識別、手寫識別等許多問題，都具有決策邊界和非線性模式。當然，線性函數也可以用于神經網絡，尤其是在輸出層。然而，對于復雜網絡，我們有大量的非線性激活函數，每個激活函數都應用于神經網絡的特定部分。最常用的包括S 型函數 (logistic)、雙曲正切函數 (tanh)、更流行且包含各種組件的整流線性單元 (ReLU)以及 Softmax。讓我們深入研究神經網絡最前沿的激活函數世界吧！

1.1. Sigmoid 激活函數

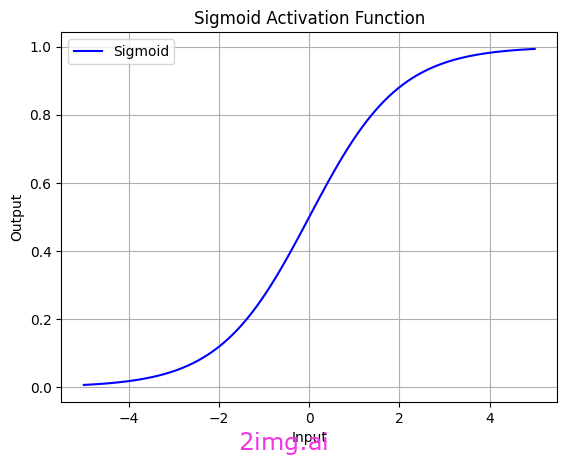
我使用 Python 代碼創建了 sigmoid 函數。

Sigmoid 函數是一種非線性函數，形狀像“S”，通常用于神經網絡中各層的輸出。默認情況下，此函數輸出(0,1)之間的值，這意味著它始終有界。換句話說，它的輸出不能小于 0 或大于 1，并且它具有正數性質。因此，它適用于分類問題和需要概率的任務。對于某些特定應用，可以使用簡單的變換來更改輸出范圍。

其數學定義由以下公式給出：

σ(x) = 1 / ( 1 + exp(-x))

這里，exp表示歐拉數（自然對數的底數），x是函數的輸入。

Sigmoid 函數的弱點之一是梯度消失問題。當 Sigmoid 函數的輸入變得非常大時，輸出趨向于 1，而當輸入非常小時，輸出趨向于 0。這導致 Sigmoid 函數的導數在這些點趨近于零，這意味著梯度變得非常小。結果，深度網絡的訓練過程可能會變得緩慢甚至停止。

1.2. 雙曲正切函數（tanh）

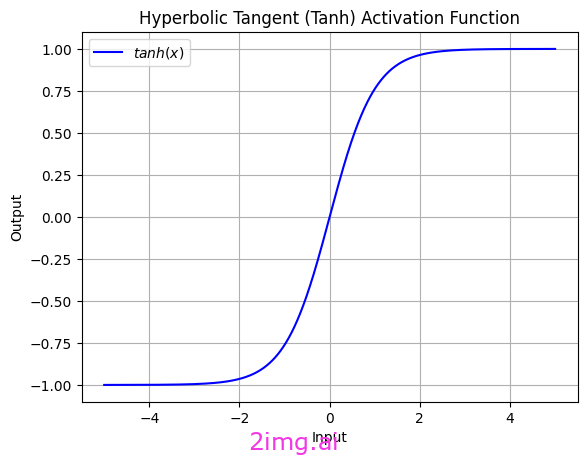
我使用 Python 代碼創建了雙曲正切函數。

雙曲正切函數 (tanh) 是一種非線性函數，類似于 S 型函數，但范圍在(-1,1)之間。這意味著它的中間值以0為中心，也包括負值。

其數學公式為：

tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))

這里，e表示歐拉數，x是函數的輸入。

tanh 和 sigmoid 激活函數都對輸出值有限制，這有助于控制梯度爆炸問題。當神經網絡的輸出值趨向于非常大或非常小的值時，梯度可能會很快變大或變小，從而導致訓練過程中出現問題。

在 tanh 函數中，輸出范圍在 (-1,1) 之間，這導致“數據居中”。這意味著它們的平均值被調整到零左右。這可以潛在地提高神經網絡的性能，因為權重不會趨向于零的任何一個極端。

在此圖中，您可以更好地理解 Sigmoid 和 Tanh 之間的區別。

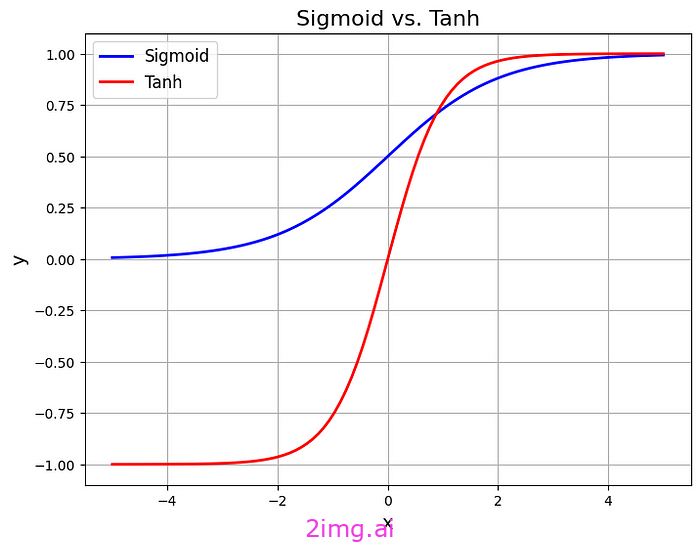
我使用 Python 代碼創建了 Sigmoid 與 Tanh

是我使用 Python 代碼創建的。

由于sigmoid函數的輸出范圍有限（0,1），神經網絡可能會遇到梯度不穩定的問題，尤其是在深度網絡中。通常，tanh因其控制梯度和數據歸一化的特性而受到青睞。

1.3. 整流線性單元（ReLU）

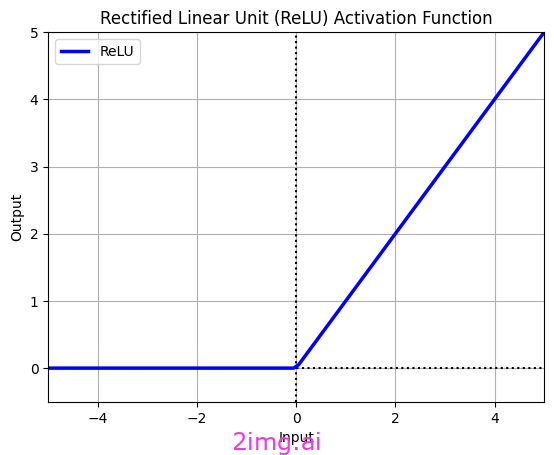
我使用 Python 代碼創建了整流線性單元 (ReLU)。

整流線性單元 (ReLU) 是人工神經網絡中最常見、最流行的非線性激活函數之一。其最主要、最重要的特點是簡單。

ReLU的計算公式如下：

f（x）=最大值（x，0）

該公式表示，如果輸入值為正，ReLU 將輸出輸入值。否則，輸出值為零，并且任何具有 ReLU 輸出為零的神經元都被視為不活躍或“死亡”。換句話說，對于小于零的輸入，ReLU 輸出一個常數零，這被稱為“稀疏性”。

該特征通過減少相互適應（當特征檢測器不是學習不同的特征，而是變得越來越相互依賴時發生）得到改進，特征檢測器（是人工神經網絡的一部分，負責識別和從數據中提取特定模式。）這種改進有助于減少過度擬合。

與 sigmoid 或 tanh 等更復雜的激活函數相比，ReLU 具有較高的計算效率，尤其是對于梯度迅速趨近于零的大值而言。ReLU 通過反向傳播提供最佳性能，因為它的梯度始終為 0 或 1，這使得訓練期間的優化更容易，并導致梯度下降。

然而，需要注意的是，ReLU 面臨“?ReLU 死亡”的問題，尤其是在網絡訓練的初始階段。“ReLU 死亡”問題是指神經網絡中的神經元使用 ReLU 激活函數進行調整，使其梯度始終為零，導致訓練期間沒有權重更新的情況。這可能導致某些神經元的訓練不足或無效，從而顯著降低網絡的性能，甚至導致網絡的某些部分完全不活躍。

1.4. 泄漏的 ReLU

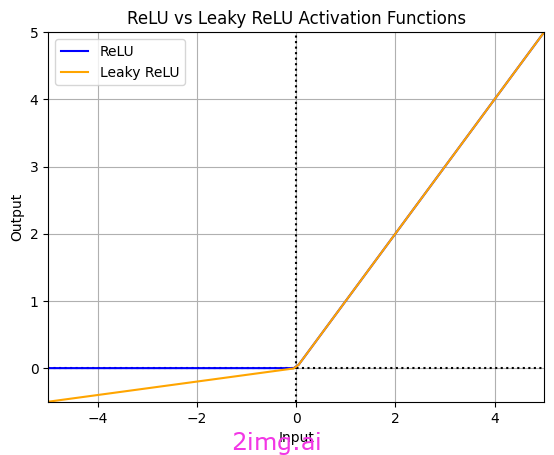
在此圖中，我們可以清楚地看到 Relu 和 Leaky ReLU 之間的區別。由我使用 Python 代碼創建

專為解決“Dying ReLU”問題而設計的 ReLU 激活函數的修改版本稱為 Leaky ReLU。在 Leaky ReLU 中，對于負值，使用非常小的斜率（例如 0.01）而不是零。因此，如果值非零，則不會發生 Dying ReLU。這使得神經網絡具有更好的訓練能力和性能，尤其是在可能遇到具有負面模式的數據時。

其數學公式為：

f (x) = { x，如果x ≥ 0ax，如果x < 0

其中a通常是一個較小的正數，一般介于0和0.01或 0.1之間

當深度神經網絡遇到不穩定梯度時，使用 Leaky ReLU 會很有幫助，因為它對負輸入的梯度很小。由于計算負輸入的斜率，Leaky ReLU 可能需要比 ReLU 更多的計算。例如，為了提高卷積神經網絡 (CNN) 在黑暗或低光圖像中的物體檢測性能（這些區域可能會丟失重要信息），或者在可能面臨稀疏梯度的生成對抗網絡 (GAN) 中，使用 Leaky ReLU 可能非常有用。

1.5.參數化 ReLU (PReLU)

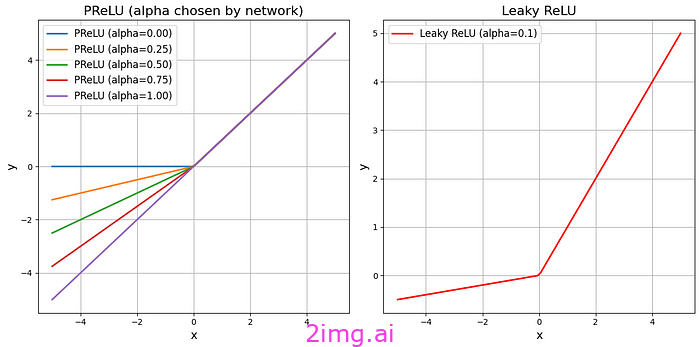
在此圖中，我們可以清楚地看到 Leaky ReLU 和參數化 ReLU (PReLU) 之間的區別。此圖是我使用 Python 代碼生成的。

ReLU 不會對帶有參數的負輸入輸出零；相反，它會為它們分配一個可學習的斜率。由于需要計算負輸入的斜率，它需要比標準 ReLU 和 Leaky ReLU 更多的計算，這增加了它的復雜性。對于靈活性和高精度至關重要的任務（例如復雜的深度神經網絡），它是有益的。

它的公式與Leaky ReLU類似，不同之處在于a的值由神經網絡在訓練過程中確定。

1.6.指數線性單元（ELU）

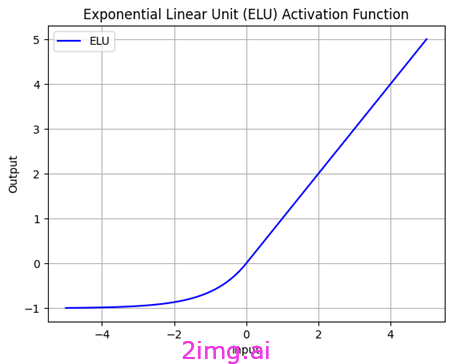
我使用 Python 代碼創建了 ELU 函數。

指數線性單元 (ELU) 是一種非線性激活函數，對于負值，它比 ReLU 更柔和。ELU 不需要參數來調整斜率；相反，它只有一個參數來調節函數的平滑度。這使得 ELU 在原點附近呈線性，并且平均而言快速接近負值，這有助于減少偏差偏移效應。這意味著模型對輸入數據和訓練偏差的響應更準確，從而獲得更好的性能。在其負部分，ELU 使用指數函數。

其計算公式如下：

f(x) = { x ，如果x ≥ 0a(e^(x^) - 1 ) ，如果x < 0

這里，a是一個正參數，充當 ELU 的斜率。此函數對于正輸入的行為類似于 ReLU，但對于負輸入則使用非線性函數。

ELU 相對于其他函數的優勢之一是可以防止Dying ReLU問題。ELU 是一種強大而靈活的激活函數，可用于廣泛的深度學習任務。

為了緩解“消亡 ReLU”的問題，可以使用諸如Leaky ReLU、參數 ReLU (PReLU)和指數線性單元 (ELU)等變體，通過引入有限的負斜率來緩解消亡 ReLU 的問題。

1.7. 縮放指數線性單元 (SELU)

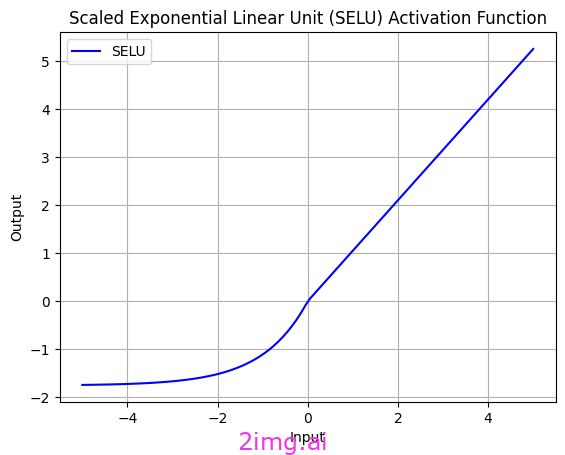
我使用 Python 代碼創建了 SELU（縮放指數線性單位）函數。

SELU（Scaled Exponential Linear Unit，縮放指數線性單元）是另一個從 ELU 派生出來的激活函數。SELU 的一個顯著優點是它的輸出是由方差為常數的分布生成的。這一特性使得使用 SELU 的小型神經網絡能夠更好地應對深度網絡中常見的梯度不穩定等問題。

其數學公式如下：

如果 x ≥ 0，則 f(x) = λ * x

如果 x < 0，則 f(x) = λ * α * (exp(x) — 1)

λ ≈ 1.0507

α ≈ 1.6733

λ 和 α是為了優化 SELU 的性能而選擇的常數值。

SELU比 ReLU 或 Leaky ReLU 等簡單激活函數更復雜。它涉及指數運算，可能需要更多計算，計算成本高昂。SELU 的參數值（例如指數系數）非常敏感，需要仔細調整。

如圖所示，SELU 在接近零時幾乎呈線性。此屬性有助于使用 SELU 訓練的神經網絡減少遇到非線性激活函數中常見的梯度消失問題等問題。

1.8.?Softmax

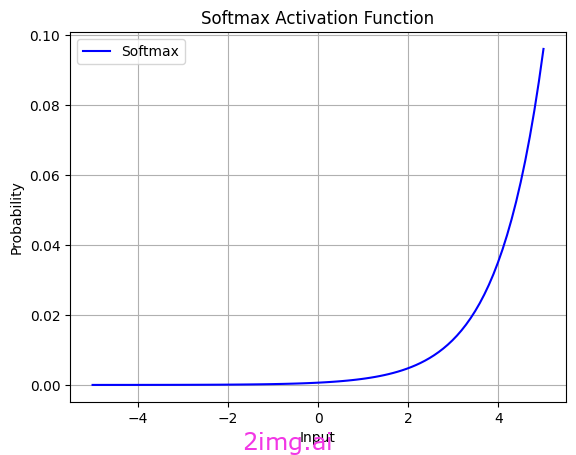
我使用 Python 代碼創建了 softmax 函數

softmax 函數，也稱為 softargmax 或正則化指數函數，將神經網絡的原始輸出轉換為概率向量。Softmax間接執行正則化。softmax 的主要目標是將輸出值轉換為概率分布，但這也隱式地對值進行了正則化。

在應用 softmax 之前，向量的某些分量可能為負或大于 1，并且它們的總和可能不等于 1。但是，在應用 softmax 之后，每個分量都落在 (0, 1) 范圍內，并且分量的總和為 1，因此它們可以解釋為概率。此外，輸入分量越大，概率也就越大。

標準softmax函數的公式為：

σ(z)_j = e^(z_j) / (∑_(k= 1 )^K e^(z_k))

標準 softmax 函數通常用于神經網絡分類器的最后一層。實際上，您可以將 softmax 視為 sigmoid 激活函數的矢量化擴展。softmax 和 sigmoid 函數都是可微分的，這對于優化算法和訓練神經網絡至關重要。例如，在反向傳播算法中，激活函數的導數用于計算梯度以更新網絡的權重和其他參數。因此，這些函數的可微分性至關重要。

S 型函數通常用于二分類問題，而 Softmax 函數用于多分類問題。但是，如果類別數為 2，則 Softmax函數會簡化為 S 型函數。

激活函數實現

在 PyTorch 或 TensorFlow 中實現激活函數時，由于常用的激活函數是預定義的，因此通常只需指定其名稱即可。這是一般規則，實現細節可能因每個激活函數而異。

在PyTorch中，激活函數使用import torch.nn as nn實現，如下面的偽代碼所示：

import torch.nn as nn # 定義一個帶有 ReLU 激活的層
relu_layer = nn.ReLU() ###################################### 
# 定義一個帶有 Sigmoid 激活的層
sigmoid_layer = nn.Sigmoid() ###################################### 
# 定義一個帶有 Tanh 激活的層
tanh_layer = nn.Tanh()

在TensorFlow中，激活函數使用“tf.keras.layers.Activation”實現，如下面的偽代碼所示：

import tensorflow as tf # 使用 ReLU 激活函數的示例
activation = tf.keras.layers.Activation( 'relu' ) # 使用 Sigmoid 激活函數的示例
activation = tf.keras.layers.Activation( 'sigmoid' ) # 使用 Tanh 激活函數的示例
activation = tf.keras.layers.Activation( 'tanh' ) # 使用 Leaky ReLU 激活函數的示例
activation = tf.keras.layers.LeakyReLU(alpha= 0.01 )   # 根據需要調整 alpha 值

2.反向傳播

反向傳播是“誤差反向傳播”的簡稱，由 Frank Rosenblatt 于 1962 年提出。如上文歷史所述，Paul Werbos 于 1974 年對其進行了進一步開發，但多年來一直未引起人們的注意。反向傳播于 1986 年首次被正式描述。

反向傳播是深度學習中的一種基本算法，它使用網絡中使用的函數的偏導數（使用鏈式法則計算）來計算損失函數相對于網絡權重的梯度。它是一種更新權重（W）的方法，以使損失函數最小化。通常，這是使用優化算法（例如隨機梯度下降（SGD）或類似變體）來完成的。

“反向傳播”是指在更新權重的同時將誤差從輸出層反向傳播到輸入層。但反向傳播到底是什么？為什么這種方法在神經網絡學習中至關重要？

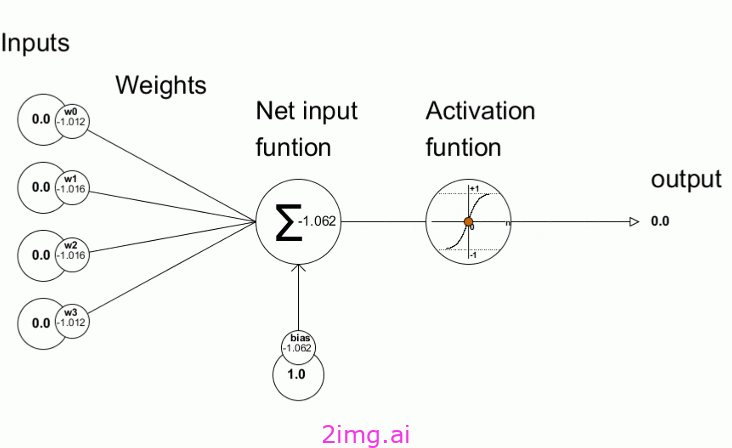
反向傳播算法由兩個階段組成：前向傳播和后向傳播。這里我先描述前向傳播階段。

2.1. 前向傳播

反向傳播算法中的前向傳遞階段是數據從輸入層傳播到輸出層并計算輸出的階段。在前向傳遞階段，非線性激活函數應用于神經網絡的不同層。例如，通常使用 ReLU（整流線性單元）。

此屬性使 ReLU 停用活動較弱的神經元（即負輸出），從而將神經網絡的注意力更多地引向數據的重要和突出特征。在前向傳遞階段，輸入值通過每層所需的激活函數，然后轉發到下一層。例如，在 PyTorch 中使用諸如“torch.relu”（用于 ReLU）之類的模塊執行此操作。使用以下偽代碼，我們可以執行其中將輸入值 x 傳遞給 torch.relu 函數并打印計算的輸出。

導入torch x = torch.tensor([- 1.0 , 0.0 , 1.0 , 2.0 ])
輸出 = torch.relu(x)
打印(輸出)

或者，使用 torch.sigmoid 模塊（用于 Sigmoid），可以使用以下代碼輕松實現。此代碼將輸入值 x 傳遞給 torch.sigmoid 函數并打印計算出的輸出。

導入torch x = torch.tensor([- 1.0 , 0.0 , 1.0 , 2.0 ])
輸出 = torch.sigmoid(x)
打印(輸出)

2.2. 損失計算

可以說，損失計算是在前向傳遞過程中進行的。數據已經通過網絡，需要為后向傳遞做好準備。因此，需要使用損失計算來計算誤差值。我們通常使用損失函數來計算這些誤差，它衡量模型預測值與實際值之間的差異。我們的目標是最小化這些誤差，以便獲得更好的數據預測模型。

在 PyTorch 中，可以使用損失函數之一輕松計算損失，例如用于分類任務的交叉熵損失。這些損失函數定義為神經網絡中的一層，計算損失值，然后作為輸入傳遞到后向傳遞階段以更新權重和偏差。值得注意的是，在 PyTorch 中，損失函數是自動計算的，您無需執行手動計算。

2.3.后向傳遞（反向傳播）

執行前向傳遞后，我們進入一個稱為反向傳遞的新階段。在反向傳遞（反向傳播）階段，誤差從輸出層傳播到輸入層。此誤差傳播使用鏈式法則從網絡末端向輸入進行。鏈式法則允許我們使用復合函數的組成函數的導數來計算復合函數的導數。此算法在訓練期間用于計算相對于網絡權重的梯度（偏導數），然后使用梯度下降等優化方法更新梯度。

總之，反向傳播有幾個階段，它使用鏈式法則將錯誤從輸出層傳播到輸入層，并計算梯度來更新權重。

您可以使用 PyTorch 庫來實現反向傳播算法。在 PyTorch 中，此過程是自動完成的，您無需手動實現。使用 PyTorch 的自動微分函數，您可以簡單地指示神經網絡如何計算損失。這段代碼將成本函數引入神經網絡。

# 定義損失函數
criterion = nn.MSELoss()

然后 PyTorch 會自動計算必要的導數并更新權重。例如，您可以使用類 torch.nn.Module 和 torch.optim 來定義神經網絡并選擇優化方法。然后，通過定義損失函數并使用 PyTorch 的自動微分函數，您可以訓練網絡。

在torch.nn.Module類中：

import torch.nn as nn # 定義一個簡單的神經網絡模型
class  SimpleModel (nn.Module): def  __init__ ( self ): super (SimpleModel, self).__init__() self.fc1 = nn.Linear( 64 , 32 )   # 定義一個輸入大小為 64、輸出大小為 32 的線性層self.fc2 = nn.Linear( 32 , 10 )   # 定義另一個輸入大小為 32、輸出大小為 10 的線性層def  forward ( self, x ): x = nn. functional.relu(self.fc1(x))   # 將 ReLU 激活函數應用于第一層的輸出x = self.fc2(x)   # 獲取第二層的輸出return x # 創建 SimpleModel 的一個實例
model = SimpleModel()

在torch.optim類中：

import torch.optim as optim # 定義模型
model = SimpleModel() # 定義優化器
optimizer = optim.SGD(model.parameters(), lr= 0.01 , influence= 0.9 ) # 定義損失函數
criterion = nn.CrossEntropyLoss() # 訓練循環內部：
# optimizer.zero_grad() # 清除梯度
# output = model(inputs) # 前向傳播
# loss = criterion(outputs, labels) # 計算損失
# loss.backward() # 后向傳播
# optimizer.step() # 更新權重

2.4. 更新權重

在經過反向傳播的所有階段，包括誤差計算、從輸出層到輸入層的誤差反向傳播以及梯度計算之后，需要更新權重。

深度學習模型中的權重是重要的參數，其值在模型訓練期間更新以提高性能。權重更新涉及以模型表現更好的方式更改權重值。此更新過程通常使用優化算法（例如梯度下降）或更高級的優化方法（例如 Adam）來完成。在某些情況下，可能已經進行了優化，并且可能不需要更新權重。

在 PyTorch 庫中，權重被表示為 `?torch.nn.Parameter`的對象，并且可以在代碼中輕松定義和管理。

import torch 
import torch.nn as nn # 定義一個有兩個輸入和一個輸出的線性層
class  LinearLayer (nn.Module): def  __init__ ( self ): super (LinearLayer, self).__init__() self.weight = nn.Parameter(torch.randn( 2 , 1 ))   # 將權重定義為參數對象self.bias = nn.Parameter(torch.randn( 1 ))   # 將偏差定義為參數對象def  forward ( self, x ): return torch.matmul(x, self.weight) + self.bias

在此代碼中，我們定義了一個具有兩個輸入和一個輸出的線性層。權重和偏差在 __init__ 函數內定義為 torch.nn.Parameter 對象。

總之，反向傳播是計算梯度和更新神經網絡權重的過程，從輸出層觀察到的誤差開始，向輸入層移動，以更新網絡權重并提高其性能。

在這一部分中，我們能夠探索重要的激活函數并了解它們背??后的邏輯。事實上，當我們使用這些函數時，我們只是調用它們，所有的計算都在后臺進行。選擇合適的激活函數有助于在網絡中實現所需的結果。當我們理解它們背后的邏輯時，我們可以更好地決定使用哪一個。我們還研究了反向傳播算法并了解了它的不同階段，熟悉了鏈式法則，它本質上是權重的導數，構成了反向傳播的基礎。反向傳播是前饋和反饋的組合，它們是網絡學習過程中的兩個重要階段。反向傳播的階段分為四個連續的階段。我們可以說，在所有神經網絡中，都存在前饋階段，因為輸入到網絡的數據的權重必須有這個階段才能進行計算并達到輸出。