WGAN
E x ~ P g [ log ? ( 1 ? D ( x ) ) ] E x ~ P g [ ? log ? D ( x ) ] \begin{aligned} & \mathbb{E}_{x \sim P_g}[\log (1-D(x))] \\ & \mathbb{E}_{x \sim P_g}[-\log D(x)] \end{aligned} ?Ex~Pg??[log(1?D(x))]Ex~Pg??[?logD(x)]?
原始 GAN 中判別器; 在 WGAN 兩篇論文中稱為 “the - log D alternative” 或 “the - log D trick”。WGAN 前作分別分析了這兩種形式的原始 GAN 各自的問題所在 .
第一種原始 GAN 形式的問題
原始 GAN 中判別器要最小化如下損失函數,盡可能把真實樣本分為正例,生成樣本分為負例:
? E x ~ P r [ log ? D ( x ) ] ? E x ~ P g [ log ? ( 1 ? D ( x ) ) ] -\mathbb{E}_{x \sim P_r}[\log D(x)]-\mathbb{E}_{x \sim P_g}[\log (1-D(x))] ?Ex~Pr??[logD(x)]?Ex~Pg??[log(1?D(x))]
一句話概括:判別器越好,生成器梯度消失越嚴重。
在生成器 G 固定參數時最優的判別器 D 應該是什么,對于一個具體樣本 x x x 它對公式 1 損失函數的貢獻是
? P r ( x ) log ? D ( x ) ? P g ( x ) log ? [ 1 ? D ( x ) ] -P_r(x) \log D(x)-P_g(x) \log [1-D(x)] ?Pr?(x)logD(x)?Pg?(x)log[1?D(x)]
? P r ( x ) D ( x ) + P g ( x ) 1 ? D ( x ) = 0 -\frac{P_r(x)}{D(x)}+\frac{P_g(x)}{1-D(x)}=0 ?D(x)Pr?(x)?+1?D(x)Pg?(x)?=0
D ? ( x ) = P r ( x ) P r ( x ) + P g ( x ) D^*(x)=\frac{P_r(x)}{P_r(x)+P_g(x)} D?(x)=Pr?(x)+Pg?(x)Pr?(x)?
如果 P r ( x ) = 0 P_r(x)=0 Pr?(x)=0且 P g ( x ) ≠ 0 P_g(x)\neq0 Pg?(x)=0 最優判別器就應該非常自信地給出概率 0;如果 P r ( x ) = P g ( x ) P_r(x)=P_g(x) Pr?(x)=Pg?(x)
說明該樣本是真是假的可能性剛好一半一半,此時最優判別器也應該給出概率 0.5。
GAN 訓練有一個 trick,就是別把判別器訓練得太好,否則在實驗中生成器會完全學不動(loss 降不下去),為了探究背后的原因,我們就可以看看在極端情況 —— 判別器最優時,生成器的損失函數變成什么。給公式 2 加上一個不依賴于生成器的項,使之變成
D ? ( x ) D^*(x) D?(x) 帶入 公式1 得到
E x ~ P r log ? P r ( x ) 1 2 [ P r ( x ) + P g ( x ) ] + E x ~ P g log ? P g ( x ) 1 2 [ P r ( x ) + P g ( x ) ] ? 2 log ? 2 \mathbb{E}_{x \sim P_r} \log \frac{P_r(x)}{\frac{1}{2}\left[P_r(x)+P_g(x)\right]}+\mathbb{E}_{x \sim P_g} \log \frac{P_g(x)}{\frac{1}{2}\left[P_r(x)+P_g(x)\right]}-2 \log 2 Ex~Pr??log21?[Pr?(x)+Pg?(x)]Pr?(x)?+Ex~Pg??log21?[Pr?(x)+Pg?(x)]Pg?(x)??2log2
K L ( P 1 ∥ P 2 ) = E x ~ P 1 log ? P 1 P 2 J S ( P 1 ∥ P 2 ) = 1 2 K L ( P 1 ∥ P 1 + P 2 2 ) + 1 2 K L ( P 2 ∥ P 1 + P 2 2 ) \begin{aligned} & K L\left(P_1 \| P_2\right)=\mathbb{E}_{x \sim P_1} \log \frac{P_1}{P_2} \\ & J S\left(P_1 \| P_2\right)=\frac{1}{2} K L\left(P_1 \| \frac{P_1+P_2}{2}\right)+\frac{1}{2} K L\left(P_2 \| \frac{P_1+P_2}{2}\right) \end{aligned} ?KL(P1?∥P2?)=Ex~P1??logP2?P1??JS(P1?∥P2?)=21?KL(P1?∥2P1?+P2??)+21?KL(P2?∥2P1?+P2??)?
2 J S ( P r ∥ P g ) ? 2 log ? 2 2 J S\left(P_r \| P_g\right)-2 \log 2 2JS(Pr?∥Pg?)?2log2
key point
在最優判別器下,我們可以把原始GAN定義的生成器loss等價變換為最小化真實分布 P r P_r Pr? 與生成分布 P g P_g Pg? 之間的JS散度。我們越訓練判別器,它就越接近最優。 最小化生成器的 loss 也就會越近似于最小化$ P_r$ 和 P g P_g Pg? 之間的JS 散度。
問題就出在這個 JS 散度上。我們會希望如果兩個分布之間越接近它們的 JS 散度越小,我們通過優化 JS 散度就能將 P g P_g Pg? "拉向" P r P_r Pr??, ,最終以假亂真。這個希望在兩個分布有所重疊的時候是成立的,但是如果兩個分布完全沒有重疊的部分,或者它們重疊的部分可忽略(下面解釋什么叫可忽略),它們的 JS 散度是多少呢? 答案是log?2,因為對于任意一個 x 只有四種可能:
P 1 ( x ) = 0 且? P 2 ( x ) = 0 P 1 ( x ) ≠ 0 且? P 2 ( x ) ≠ 0 P 1 ( x ) = 0 且? P 2 ( x ) ≠ 0 P 1 ( x ) ≠ 0 且? P 2 ( x ) = 0 \begin{aligned} & P_1(x)=0 \text { 且 } P_2(x)=0 \\ & P_1(x) \neq 0 \text { 且 } P_2(x) \neq 0 \\ & P_1(x)=0 \text { 且 } P_2(x) \neq 0 \\ & P_1(x) \neq 0 \text { 且 } P_2(x)=0 \end{aligned} ?P1?(x)=0?且?P2?(x)=0P1?(x)=0?且?P2?(x)=0P1?(x)=0?且?P2?(x)=0P1?(x)=0?且?P2?(x)=0?
- 第一種對計算 JS 散度無貢獻
- 第二種情況由于重疊部分可忽略所以貢獻也為 0
- 第三種情況對公式 7 右邊第一個項的貢獻 log ? P 2 1 2 ( P 2 + 0 ) = log ? 2 \log \frac{P_2}{\frac{1}{2}\left(P_2+0\right)}=\log 2 log21?(P2?+0)P2??=log2
- 第四種情況 J S ( P 1 ∥ P 2 ) = log ? 2 J S\left(P_1 \| P_2\right)=\log 2 JS(P1?∥P2?)=log2
即無論 P r P_r Pr? 跟 P g P_g Pg? 是遠在天邊,還是近在眼前,只要它們倆沒有一點重疊或者重疊部分可忽略,JS 散度就固定是常數log?2, 而這對于梯度下降方法意味著 —— 梯度為 0.此時對于最優判別器來說,生成器肯定是得不到一丁點梯度信息的;即使對于接近最優的判別器來說,生成器也有很大機會面臨梯度消失的問題。
Manifold A topological space that locally resembles Euclidean space near each point when this Euclidean space is of dimension n n n ,the manifold is referred as manifold.
- 支撐集(support)其實就是函數的非零部分子集,比如 ReLU 函數的支撐集就是(0,+∞),一個概率分布的支撐集就是所有概率密度非零部分的集合。
- 流形(manifold)是高維空間中曲線、曲面概念的拓廣,我們可以在低維上直觀理解這個概念,比如我們說三維空間中的一個曲面是一個二維流形,因為它的本質維度(intrinsic dimension)只有 2,一個點在這個二維流形上移動只有兩個方向的自由度。同理,三維空間或者二維空間中的一條曲線都是一個一維流形。
P r Pr Pr 已發現它們集中在較低維流形中。這實際上是流形學習的基本假設。想想現實世界的圖像,一旦主題或所包含的對象固定,圖像就有很多限制可以遵循,例如狗應該有兩只耳朵和一條尾巴,摩天大樓應該有筆直而高大的身體,等等。這些限制使圖像無法具有高維自由形式。
P g P_g Pg? 也存在于低維流形中。每當生成器被要求提供更大的圖像(例如 64x64),給定小尺寸(例如 100),噪聲變量輸入 z z z 這4096個像素的顏色分布是由100維的小隨機數向量定義的,很難填滿整個高維空間。
P r P_r Pr? 和 P g P_g Pg? 不重疊或重疊部分可忽略的可能性有多大?不嚴謹的答案是:非常大。
both P r P_r Pr? and p g p_g pg? 處于低維流形中,他們幾乎不會相交。(wgan 前面一篇理論證明)
GAN 中的生成器一般是從某個低維(比如 100 維)的隨機分布中采樣出一個編碼向量 z z z,再經過一個神經網絡生成出一個高維樣本(比如 64x64 的圖片就有 4096 維)。當生成器的參數固定時,生成樣本的概率分布雖然是定義在 4096 維的空間上,但它本身所有可能產生的變化已經被那個 100 維的隨機分布限定了,其本質維度就是 100,再考慮到神經網絡帶來的映射降維,最終可能比 100 還小,所以生成樣本分布的支撐集就在 4096 維空間中構成一個最多 100 維的低維流形,“撐不滿” 整個高維空間。
在這里插入圖片描述
我們就得到了 WGAN 前作中關于生成器梯度消失的第一個論證:在(近似)最優判別器下,最小化生成器的 loss 等價于最小化 P r P_r Pr? 與 P g P_g Pg? 之間的JS散度,而由于 P r P_r Pr? 與 P g P_g Pg? 幾乎不可能有不可忽略的重疊,所以無論它們相距多遠 JS 散度都是常數log?2,最終導致生成器的梯度(近似)為 0,梯度消失。
原始 GAN 不穩定的原因就徹底清楚了:判別器訓練得太好,生成器梯度消失,生成器 loss 降不下去;判別器訓練得不好,生成器梯度不準,四處亂跑。只有判別器訓練得不好不壞才行,但是這個火候又很難把握,甚至在同一輪訓練的前后不同階段這個火候都可能不一樣,所以 GAN 才那么難訓練。
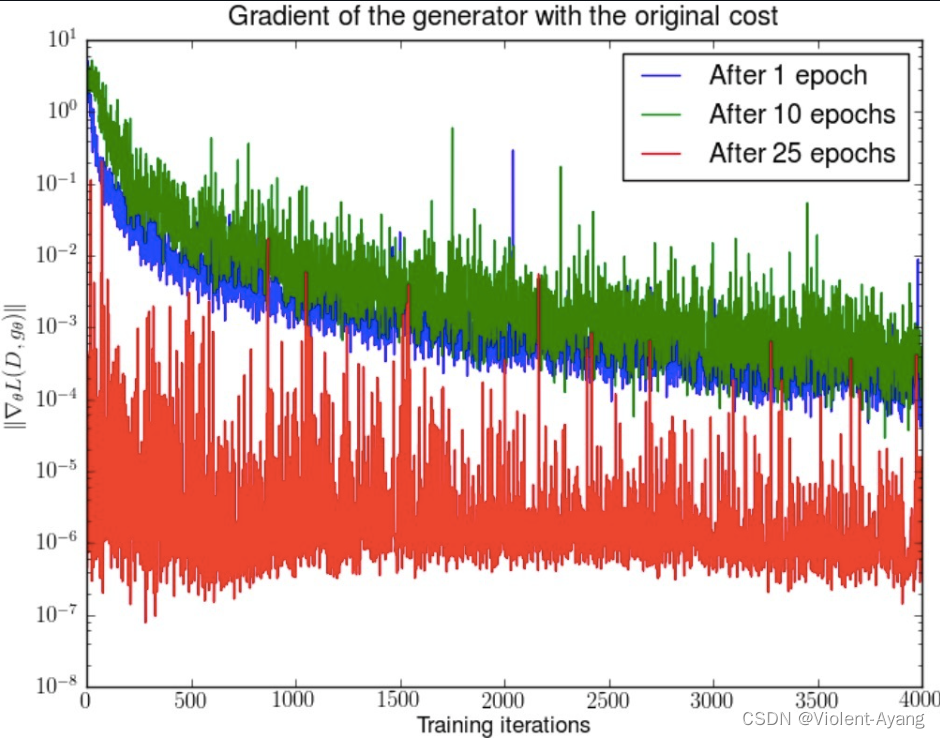
第二種原始 GAN 形式的問題 “the - log D trick”
一句話概括:最小化第二種生成器 loss 函數,會等價于最小化一個不合理的距離衡量,導致兩個問題,一是梯度不穩定,二是 **Mode collapse 即多樣性不足。**WGAN 前作又是從兩個角度進行了論證
上文推導已經得到在最優判別器 D ? D^* D? 下
E x ~ P r [ log ? D ? ( x ) ] + E x ~ P g [ log ? ( 1 ? D ? ( x ) ) ] = 2 J S ( P r ∥ P g ) ? 2 log ? 2 \mathbb{E}_{x \sim P_r}\left[\log D^*(x)\right]+\mathbb{E}_{x \sim P_g}\left[\log \left(1-D^*(x)\right)\right]=2 J S\left(P_r \| P_g\right)-2 \log 2 Ex~Pr??[logD?(x)]+Ex~Pg??[log(1?D?(x))]=2JS(Pr?∥Pg?)?2log2
K L ( P g ∥ P r ) = E x ~ P g [ log ? P g ( x ) P r ( x ) ] = E x ~ P g [ log ? P g ( x ) / ( P r ( x ) + P g ( x ) ) P r ( x ) / ( P r ( x ) + P g ( x ) ) ] = E x ~ P g [ log ? 1 ? D ? ( x ) D ? ( x ) ] = E x ~ P g log ? [ 1 ? D ? ( x ) ] ? E x ~ P g log ? D ? ( x ) \begin{aligned} K L\left(P_g \| P_r\right) & =\mathbb{E}_{x \sim P_g}\left[\log \frac{P_g(x)}{P_r(x)}\right] \\ & =\mathbb{E}_{x \sim P_g}\left[\log \frac{P_g(x) /\left(P_r(x)+P_g(x)\right)}{P_r(x) /\left(P_r(x)+P_g(x)\right)}\right] \\ & =\mathbb{E}_{x \sim P_g}\left[\log \frac{1-D^*(x)}{D^*(x)}\right] \\ & =\mathbb{E}_{x \sim P_g} \log \left[1-D^*(x)\right]-\mathbb{E}_{x \sim P_g} \log D^*(x) \end{aligned} KL(Pg?∥Pr?)?=Ex~Pg??[logPr?(x)Pg?(x)?]=Ex~Pg??[logPr?(x)/(Pr?(x)+Pg?(x))Pg?(x)/(Pr?(x)+Pg?(x))?]=Ex~Pg??[logD?(x)1?D?(x)?]=Ex~Pg??log[1?D?(x)]?Ex~Pg??logD?(x)?
E x ~ P g [ ? log ? D ? ( x ) ] = K L ( P g ∥ P r ) ? E x ~ P g log ? [ 1 ? D ? ( x ) ] = K L ( P g ∥ P r ) ? 2 J S ( P r ∥ P g ) + 2 log ? 2 + E x ~ P r [ log ? D ? ( x ) ] \begin{aligned} \mathbb{E}_{x \sim P_g}\left[-\log D^*(x)\right] & =K L\left(P_g \| P_r\right)-\mathbb{E}_{x \sim P_g} \log \left[1-D^*(x)\right] \\ & =K L\left(P_g \| P_r\right)-2 J S\left(P_r \| P_g\right)+2 \log 2+\mathbb{E}_{x \sim P_r}\left[\log D^*(x)\right] \end{aligned} Ex~Pg??[?logD?(x)]?=KL(Pg?∥Pr?)?Ex~Pg??log[1?D?(x)]=KL(Pg?∥Pr?)?2JS(Pr?∥Pg?)+2log2+Ex~Pr??[logD?(x)]?
注意上式最后兩項不依賴于生成器 G G G ,最終得到最小化公式 3 等價于最小化 K L ( P g ∥ P r ) ? 2 J S ( P r ∥ P g ) K L\left(P_g \| P_r\right)-2 J S\left(P_r \| P_g\right) KL(Pg?∥Pr?)?2JS(Pr?∥Pg?)
這個等價最小化目標存在兩個嚴重的問題。第一是它同時要最小化生成分布與真實分布的 KL 散度,卻又要最大化兩者的 JS 散度,一個要拉近,一個卻要推遠!這在直觀上非常荒謬,在數值上則會導致梯度不穩定,這是后面那個 JS 散度項的毛病。
第二,即便是前面那個正常的 KL 散度項也有毛病。因為 KL 散度不是一個對稱的衡量 K L ( P g ∥ P r ) K L\left(P_g \| P_r\right) KL(Pg?∥Pr?) 與 K L ( P r ∥ P g ) K L\left(P_r \| P_g\right) KL(Pr?∥Pg?) 是有差別的。
Wasserstein 距離的優越性質
W ( P r , P g ) = inf ? γ ~ Π ( P r , P g ) E ( x , y ) ~ γ [ ∥ x ? y ∥ ] W\left(P_r, P_g\right)=\inf _{\gamma \sim \Pi\left(P_r, P_g\right)} \mathbb{E}_{(x, y) \sim \gamma}[\|x-y\|] W(Pr?,Pg?)=γ~Π(Pr?,Pg?)inf?E(x,y)~γ?[∥x?y∥]
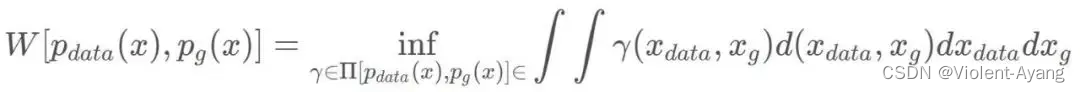
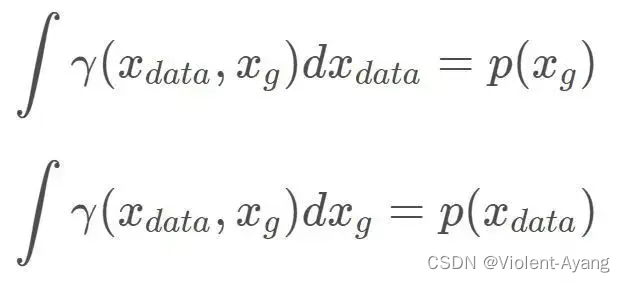

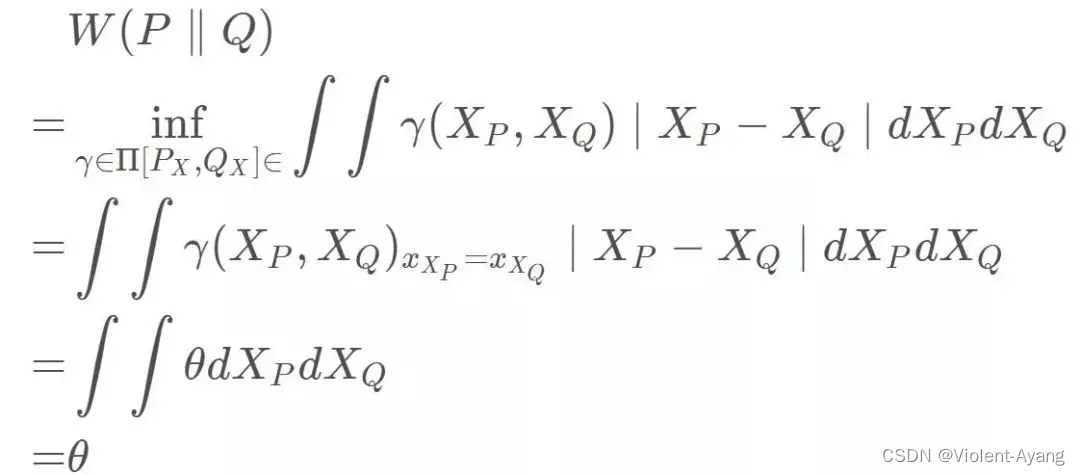
可以看出 Wasserstein 距離處處連續,而且幾乎處處可導,數學性質非常好,能夠在兩個分布沒有重疊部分的時候,依舊給出合理的距離度量。對于離散概率分布,Wasserstein 距離也被描述性地稱為推土機距離 (EMD)。 如果我們將分布想象為一定量地球的不同堆,那么 EMD 就是將一個堆轉換為另一堆所需的最小總工作量。
解釋如下: Π ( P r , P g ) \Pi\left(P_r, P_g\right) Π(Pr?,Pg?) 是 P r P_r Pr? 和 P g P_g Pg? 組合起來的所有可能的聯合分布的集合,反過來說, Π ( P r , P g ) \Pi\left(P_r, P_g\right) Π(Pr?,Pg?) 中每一個分布的邊緣分布都是 P r P_r Pr? 和 P g P_g Pg? 。對于每一個可能的聯合分布 γ \gamma γ 而言,可以從 中采樣 ( x , y ) ~ γ (x, y) \sim \gamma (x,y)~γ 得到一個真實樣本 x x x 和一個生成樣本 y y y ,并算出這對樣本的距離 ∥ x ? y ∥ \|x-y\| ∥x?y∥ ,所 以可以計算該聯合分布 γ \gamma γ 下樣本對距離的期望值 E ( x , y ) ~ γ [ ∥ x ? y ∥ ] \mathbb{E}_{(x, y) \sim \gamma}[\|x-y\|] E(x,y)~γ?[∥x?y∥] 。在所有可能的聯合分布中 夠對這個期望值取到的下界inf in ? γ ~ ( P r , P g ) E ( x , y ) ~ γ [ ∥ x ? y ∥ ] \operatorname{in}_{\gamma \sim\left(P_r, P_g\right)} \mathbb{E}_{(x, y) \sim \gamma}[\|x-y\|] inγ~(Pr?,Pg?)?E(x,y)~γ?[∥x?y∥] ,就定義為 Wasserstein 距離。
直觀上可以把 E ( x , y ) ~ γ [ ∥ x ? y ∥ ] \mathbb{E}_{(x, y) \sim \gamma}[\|x-y\|] E(x,y)~γ?[∥x?y∥] 理解為在 γ \gamma γ 這個 “路徑規劃" 下把 P r P_r Pr? 這堆 “沙土" 挪到 P g P_g Pg? “位置” 所需的 “消耗”, 而 W ( P r , P g ) W\left(P_r, P_g\right) W(Pr?,Pg?) 就是 “最優路徑規劃" 下的 “最小消耗”,所以才 叫 Earth-Mover (推土機 ) 距離。
Wasserstein 距離相比 KL 散度、JS 散度的優越性在于,即便兩個分布沒有重疊,Wasserstein 距離仍然能夠反映它們的遠近。WGAN 本作通過簡單的例子展示了這一點。考慮如下二維空間中 的兩個分布 P 1 P_1 P1? 和 P 2 , P 1 P_2 , P_1 P2?,P1? 在線段 A B \mathrm{AB} AB 上均勻分布, P 2 P_2 P2? 在線段 C D \mathrm{CD} CD 上均勻分布,通過控制參數 θ \theta θ 可以控制著兩個分布的距離遠近。
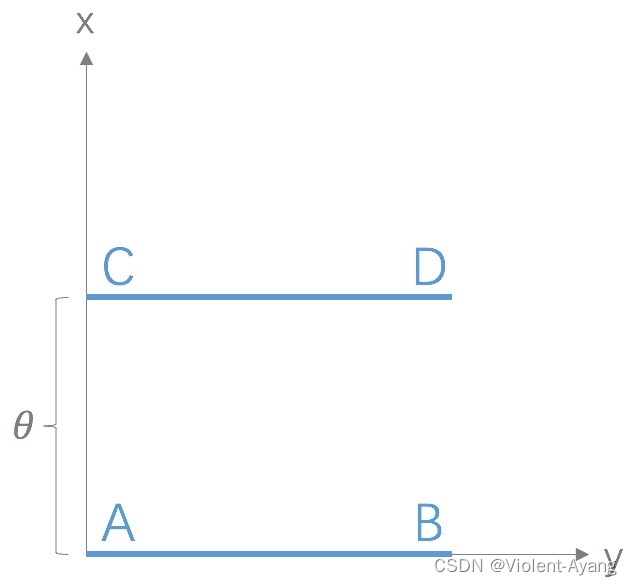
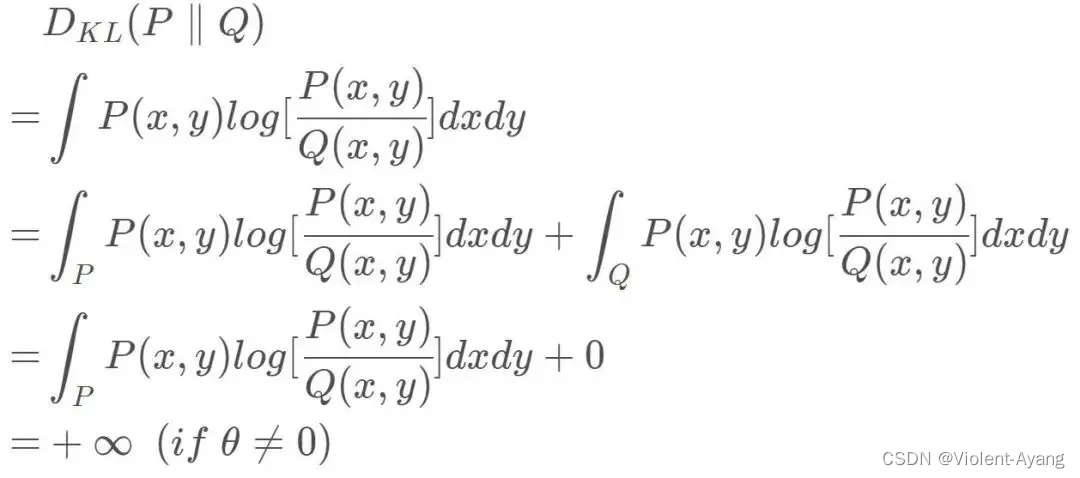
K L ( P 1 ∥ P 2 ) = K L ( P 1 ∣ ∣ P 2 ) = { + ∞ if? θ ≠ 0 0 if? θ = 0 (突變)? J S ( P 1 ∥ P 2 ) = { log ? 2 if? θ ≠ 0 0 if? θ ? 0 (突變?)? W ( P 0 , P 1 ) = ∣ θ ∣ (平滑?)? \begin{aligned} & K L\left(P_1 \| P_2\right)=K L\left(P_1|| P_2\right)=\left\{\begin{array}{ll} +\infty & \text { if } \theta \neq 0 \\ 0 & \text { if } \theta=0 \end{array}\right. \text { (突變) } \\ & J S\left(P_1 \| P_2\right)=\left\{\begin{array}{ll} \log 2 & \text { if } \theta \neq 0 \\ 0 & \text { if } \theta-0 \end{array}\right. \text { (突變 ) } \\ & W\left(P_0, P_1\right)=|\theta| \text { (平滑 ) } \end{aligned} ?KL(P1?∥P2?)=KL(P1?∣∣P2?)={+∞0??if?θ=0?if?θ=0??(突變)?JS(P1?∥P2?)={log20??if?θ=0?if?θ?0??(突變?)?W(P0?,P1?)=∣θ∣?(平滑?)??
第四部分:從 Wasserstein 距離到 WGAN
EMD ? ( P r , P θ ) = inf ? γ ∈ Π ∑ x , y ∥ x ? y ∥ γ ( x , y ) = inf ? γ ∈ Π E ( x , y ) ~ γ ∥ x ? y ∥ \operatorname{EMD}\left(P_r, P_\theta\right)=\inf _{\gamma \in \Pi} \sum_{x, y}\|x-y\| \gamma(x, y)=\inf _{\gamma \in \Pi} \mathbb{E}_{(x, y) \sim \gamma}\|x-y\| EMD(Pr?,Pθ?)=γ∈Πinf?x,y∑?∥x?y∥γ(x,y)=γ∈Πinf?E(x,y)~γ?∥x?y∥
It is intractable to exhaust all the possible joint distributions in Π ( p r , p g ) \Pi\left(p_r, p_g\right) Π(pr?,pg?) to compute inf ? γ ~ Π ( p r , p g ) \inf _{\gamma \sim \Pi\left(p_r, p_g\right)} infγ~Π(pr?,pg?)? Thus the authors proposed a smart transformation of the formula based on the KantorovichRubinstein duality to: 作者提出了基于 Kantorovich-Rubinstein 對偶性的公式的巧妙轉換:
W ( p r , p g ) = 1 K sup ? ∥ f ∥ L ≤ K E x ~ p r [ f ( x ) ] ? E x ~ p g [ f ( x ) ] W\left(p_r, p_g\right)=\frac{1}{K} \sup _{\|f\| L \leq K} \mathbb{E}_{x \sim p_r}[f(x)]-\mathbb{E}_{x \sim p_g}[f(x)] W(pr?,pg?)=K1?∥f∥L≤Ksup?Ex~pr??[f(x)]?Ex~pg??[f(x)]
首先需要介紹一個概念——Lipschitz 連續。它其實就是在一個連續函數 f f f 上面額外施加了一個限 制,要求存在一個常數 K ≥ 0 K \geq 0 K≥0 使得定義域內的任意兩個元素 x 1 x_1 x1? 和 x 2 x_2 x2? 都滿足
∣ f ( x 1 ) ? f ( x 2 ) ∣ ≤ K ∣ x 1 ? x 2 ∣ \left|f\left(x_1\right)-f\left(x_2\right)\right| \leq K\left|x_1-x_2\right| ∣f(x1?)?f(x2?)∣≤K∣x1??x2?∣
此時稱函數 f f f 的 Lipschitz 常數為 K K K 。
上述公式 的意思就是在要求函數 f f f 的 Lipschitz 常數 ∣ f ∥ L \mid f \|_L ∣f∥L? 不超過 K K K 的條件下,對所有可能滿足 件的 f f f 取到趻 數 w w w 來定義一系列可能的函數 f w f_w fw? ,此時求解公式 可以近似變成求解如下形式
K ? W ( P r , P g ) ≈ max ? w : ∣ f w ∣ L ≤ K E x ~ P r [ f w ( x ) ] ? E x ~ P g [ f w ( x ) ] K \cdot W\left(P_r, P_g\right) \approx \max _{w:\left|f_w\right|_L \leq K} \mathbb{E}_{x \sim P_r}\left[f_w(x)\right]-\mathbb{E}_{x \sim P_g}\left[f_w(x)\right] K?W(Pr?,Pg?)≈w:∣fw?∣L?≤Kmax?Ex~Pr??[fw?(x)]?Ex~Pg??[fw?(x)]
W ( p r , p θ ) = inf ? γ ∈ π ? ∥ x ? y ∥ γ ( x , y ) d x d y = inf ? γ ∈ π E x , y ~ γ [ ∥ x ? y ∥ ] . W\left(p_r, p_\theta\right)=\inf _{\gamma \in \pi} \iint\|x-y\| \gamma(x, y) \mathrm{d} x \mathrm{~d} y=\inf _{\gamma \in \pi} \mathbb{E}_{x, y \sim \gamma}[\|x-y\|] . W(pr?,pθ?)=γ∈πinf??∥x?y∥γ(x,y)dx?dy=γ∈πinf?Ex,y~γ?[∥x?y∥].
W ( p r , p θ ) = inf ? γ ∈ π E x , y ~ γ [ ∥ x ? y ∥ ] = inf ? γ E x , y ~ γ [ ∥ x ? y ∥ + sup ? f E s ~ p r [ f ( s ) ] ? E t ~ p θ [ f ( t ) ] ? ( f ( x ) ? f ( y ) ) ] ? = { 0 , if? γ ∈ π + ∞ else? = inf ? γ sup ? f E x , y ~ γ [ ∥ x ? y ∥ + E s ~ p r [ f ( s ) ] ? E t ~ p θ [ f ( t ) ] ? ( f ( x ) ? f ( y ) ) ] \begin{aligned} W\left(p_r, p_\theta\right) & =\inf _{\gamma \in \pi} \mathbb{E}_{x, y \sim \gamma}[\|x-y\|] \\ & =\inf _\gamma \mathbb{E}_{x, y \sim \gamma}[\|x-y\|+\underbrace{\left.\sup _f \mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)]-(f(x)-f(y))\right]} \\ & =\left\{\begin{array}{c} 0, \text { if } \gamma \in \pi \\ +\infty \text { else } \end{array}\right. \\ & =\inf _\gamma \sup _f \mathbb{E}_{x, y \sim \gamma}\left[\|x-y\|+\mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)]-(f(x)-f(y))\right] \end{aligned} W(pr?,pθ?)?=γ∈πinf?Ex,y~γ?[∥x?y∥]=γinf?Ex,y~γ?[∥x?y∥+ fsup?Es~pr??[f(s)]?Et~pθ??[f(t)]?(f(x)?f(y))]?={0,?if?γ∈π+∞?else??=γinf?fsup?Ex,y~γ?[∥x?y∥+Es~pr??[f(s)]?Et~pθ??[f(t)]?(f(x)?f(y))]?
sup ? f inf ? γ E x , y ~ γ [ ∥ x ? y ∥ + E s ~ p r [ f ( s ) ] ? E t ~ p θ [ f ( t ) ] ? ( f ( x ) ? f ( y ) ) ] = sup ? f E s ~ p r [ f ( s ) ] ? E t ~ p θ [ f ( t ) ] + inf ? γ E x , y ~ γ [ ∥ x ? y ∥ ? ( f ( x ) ? f ( y ) ) ] ? γ = { 0 , if? ∥ f ∥ L ≤ 1 ? ∞ else? \begin{array}{r} \sup _f \inf _\gamma \mathbb{E}_{x, y \sim \gamma}\left[\|x-y\|+\mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)]-(f(x)-f(y))\right] \\ =\sup _f \mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)]+\underbrace{\inf _\gamma \mathbb{E}_{x, y \sim \gamma}[\|x-y\|-(f(x)-f(y))]}_\gamma \\ =\left\{\begin{array}{cc} 0, & \text { if }\|f\|_L \leq 1 \\ -\infty & \text { else } \end{array}\right. \end{array} supf?infγ?Ex,y~γ?[∥x?y∥+Es~pr??[f(s)]?Et~pθ??[f(t)]?(f(x)?f(y))]=supf?Es~pr??[f(s)]?Et~pθ??[f(t)]+γ γinf?Ex,y~γ?[∥x?y∥?(f(x)?f(y))]??={0,?∞??if?∥f∥L?≤1?else???
W ( p r , p θ ) = sup ? f E s ~ p r [ f ( s ) ] ? E t ~ p θ [ f ( t ) ] + inf ? γ E x , y ~ γ [ ∥ x ? y ∥ ? ( f ( x ) ? f ( y ) ) ] = sup ? ∥ f ∥ L ≤ 1 E s ~ p r [ f ( s ) ] ? E t ~ p θ [ f ( t ) ] \begin{aligned} W\left(p_r, p_\theta\right) & =\sup _f \mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)]+\inf _\gamma \mathbb{E}_{x, y \sim \gamma}[\|x-y\|-(f(x)-f(y))] \\ & =\sup _{\|f\|_{L \leq 1}} \mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)] \end{aligned} W(pr?,pθ?)?=fsup?Es~pr??[f(s)]?Et~pθ??[f(t)]+γinf?Ex,y~γ?[∥x?y∥?(f(x)?f(y))]=∥f∥L≤1?sup?Es~pr??[f(s)]?Et~pθ??[f(t)]?







![FIND_IN_SET使用案例--[sql語句根據多ids篩選出對應數據]](http://pic.xiahunao.cn/FIND_IN_SET使用案例--[sql語句根據多ids篩選出對應數據])









)

