DFS之剪枝與優化

定義

DFS之剪枝與優化指的是在執行深度優先搜索(DFS, Depth-First Search)時，采取的一系列策略來減少搜索空間，避免無效計算，從而加速找到問題的解。剪枝是指在搜索過程中，當遇到某些條件不符合解的要求或者可以預判后續搜索不會產生有效解時，直接放棄這條搜索路徑，這一過程稱為剪枝。優化則是指通過調整搜索策略、順序等，提高搜索效率。

運用情況

1. 組合優化問題：如全排列、組合總和、子集問題等，剪枝可以避免生成無效解。
2. 圖的遍歷與搜索：在尋找特定路徑或計算連通分量時，剪枝可以減少搜索范圍。
3. 游戲AI：如棋類游戲中預測對手可能的走法，剪枝減少計算量。
4. 約束滿足問題：如數獨、任務調度等，剪枝幫助快速排除不滿足條件的解。

注意事項

1. 剪枝條件的選擇：剪枝條件應嚴格且準確，避免誤剪有效解。
2. 搜索順序：合理安排搜索順序，優先探索最有希望的分支。
3. 狀態重置：回溯時確保正確恢復現場，避免狀態污染。
4. 記憶化：對于重復子問題，使用記憶化技術存儲中間結果，避免重復計算。
5. 資源管理：注意棧或遞歸深度限制，防止棧溢出。

解題思路

1. 明確剪枝條件：分析問題特性，確定何時可以安全地剪枝。
2. 優化搜索順序：
   • 分支較少優先：優先探索分支較少的路徑，減少搜索深度。
   • 啟發式排序：依據某種評估函數排序待探索節點，優先探索最有潛力的節點。
3. 可行性剪枝：在探索前，如果可以證明當前路徑無法導致有效解，立即剪枝。
4. 最優性剪枝：在某些最優化問題中，如果已知當前路徑不能優于已找到的最佳解，剪枝。
5. 迭代加深DFS：結合深度限制，逐步增加深度限制進行搜索，適用于尋找最短路徑等問題。
6. 記憶化搜索：在適用場景下，利用動態規劃思想存儲中間結果，避免重復計算。

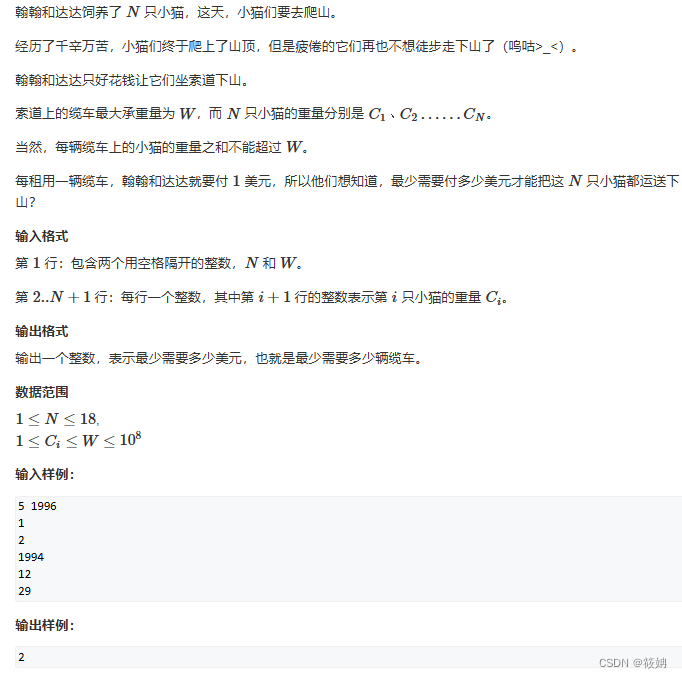
AcWing 165. 小貓爬山

題目描述

165. 小貓爬山 - AcWing題庫

運行代碼

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20;int n, m;
int w[N];
int sum[N];
int ans = N;void dfs(int u, int k)
{if(k >= ans) return;if(u == n){ans = k;return;}for(int i = 0; i < k; i ++ )if(sum[i] + w[u] <= m){sum[i] += w[u];dfs(u + 1, k);sum[i] -= w[u];}sum[k] = w[u];dfs(u + 1, k + 1);sum[k] = 0;
}int main()
{cin >> n >> m;for(int i = 0; i < n; i ++ ) cin >> w[i];sort(w, w + n, greater<int>());dfs(0, 0);cout << ans << endl;return 0;
}

代碼思路

1. 輸入與初始化：讀取小貓數量?n?和纜車最大承重?m，以及每只小貓的重量?w[]，并按重量從大到小排序。
2. DFS搜索：定義一個深度優先搜索函數?dfs(u, k)，其中?u?是當前考慮的小貓索引，k?是當前已經考慮過的纜車數量。
   • 當搜索到的纜車數量?k?大于或等于已知的最小纜車數量?ans?時，提前結束此分支的搜索。
   • 當所有小貓都被考慮過后，更新最小纜車數量?ans。
   • 對于每輛纜車，嘗試將當前小貓放入（如果總重不超過?m），遞歸搜索下一個位置的小貓。遞歸結束后回溯，撤銷選擇。
3. 主函數邏輯：初始化數組?sum[]?用于記錄每輛纜車的當前載重，然后調用?dfs()?函數，最后輸出最小纜車數量?ans。

其它代碼

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20;int n, m;
int w[N];
int sum[N];
int ans = N;void dfs(int u, int k)
{if(k >= ans) return;if(u == n){ans = k;return;}for(int i = 0; i < k; i ++ )if(sum[i] + w[u] <= m){sum[i] += w[u];dfs(u + 1, k);sum[i] -= w[u];}sum[k] = w[u];dfs(u + 1, k + 1);sum[k] = 0;
}int main()
{cin >> n >> m;for(int i = 0; i < n; i ++ ) cin >> w[i];//sort(w, w + n, greater<int>());dfs(0, 0);cout << ans << endl;return 0;
}

代碼思路

1. 變量定義:

   • n: 表示小貓的數量。
   • m: 表示每輛纜車的最大承重。
   • w[N]: 存儲每只小貓的重量。
   • sum[N]: 記錄每輛纜車當前的總重量。
   • ans: 初始設置為一個較大的數（N），用于記錄最少需要的纜車數量，最終會被更新為實際的最小數量。

2. 主函數邏輯:

   • 讀取小貓數量?n?和纜車最大承重?m。
   • 輸入每只小貓的重量?w[]。注意代碼中去掉了原先對w[]進行排序的部分，這在原始代碼中是為了優化搜索過程，因為通常按照重量從大到小處理可以更快達到最優解，但這里為了保持原始邏輯解釋，未進行排序。
   • 調用深度優先搜索函數?dfs(u, k)?進行求解，其中?u?表示當前考慮的小貓索引（從0開始），k?表示當前已經分配的纜車數量。
   • 輸出最少纜車數量?ans。

3. 深度優先搜索 (DFS) 函數邏輯:

   • 剪枝條件: 當已分配的纜車數量?k?大于等于已知的最小纜車數量?ans?時，直接返回，因為后續的搜索不會得到更好的解。
   • 終止條件: 當所有小貓都被考慮過（即?u == n）時，更新?ans?為當前的纜車數量?k，然后返回。
   • 嘗試分配小貓到已有纜車:
     • 遍歷之前的所有纜車（用?i?表示），檢查當前小貓是否能加入到纜車?i?中（即?sum[i] + w[u] <= m）。
       • 如果可以加入，就臨時增加?sum[i]?的值，然后遞歸調用?dfs?函數嘗試分配下一個貓，分配完后再恢復?sum[i]?的值（回溯）。
   • 嘗試分配到新纜車:
     • 將當前小貓分配到一個新的纜車（即?sum[k] = w[u]），然后遞歸調用?dfs?函數分配下一個貓，分配完后清空?sum[k]（因為這是嘗試過程中的狀態，不是最終分配）。