本節及后續章節將介紹機器學習中的幾種經典回歸算法，所選方法都在Sklearn庫中聚類模塊有具體實現。本節為上篇，將介紹基礎的線性回歸方法，包括線性回歸、邏輯回歸、多項式回歸和嶺回歸等。

2.1 回歸分析概述

回歸（Regression）分析是機器學習領域中最古老、最基礎，同時也是最廣泛應用的問題之一，應用十分廣泛。

簡而言之，回歸分析旨在建立一個模型，使用這個模型可以用一組特征（自變量）來預測一個連續的結果（因變量）。舉一個容易理解的例子，我們可以使用房間的面積、樓層、位置、周邊配套等特征來預測該商品房的房價高低，在這個例子中，房價是因變量，且是連續變化的，可以在一定非負區間內取任何實數值，而影響房價的各個因素，成為自變量，自變量可以是各種類型的值，但為了回歸分析方便，通常將自變量也轉換為數值類型。

2.1.1 回歸與分類

回歸問題是預測一個連續值的輸出（因變量）基于一個或多個輸入（自變量或特征）的機器學習任務。換句話說，回歸模型嘗試找到自變量和因變量之間的內在關系。

回歸和分類是兩類典型的監督學習問題，兩者的主要區別在于輸出類型和評價指標不同，如下：

• 輸出類型：回歸模型通常用來預測連續值（如價格、溫度等），分類模型用來預測離散標簽（如0/1）。
• 評估指標：回歸通常使用均方誤差（MSE）、R2分數等作為評估指標，而分類則使用準確率、F1分數等。

2.1.2 常見的回歸方法

在此主要介紹Sklearn中實現的幾類典型的回歸方法，

• 線性回歸：線性回歸是回歸問題中最簡單也最常用的一種算法。它的基本思想是通過找到最佳擬合直線來模擬因變量和自變量之間的關系。
• 多項式回歸：與線性回歸嘗試使用直線擬合數據不同，多項式回歸使用多項式方程進行擬合。
• 支持向量回歸：它是支持向量機（SVM）的回歸版本，用于解決回歸問題。它試圖找到一個超平面，以便在給定容忍度內最大程度地減小預測和實際值之間的誤差。
• 決策樹回歸：它是一種非參數的、基于樹結構的回歸方法。它通過將特征空間劃分為一組簡單的區域，并在每個區域內進行預測。

回歸算法全解析！一文讀懂機器學習中的回歸模型-騰訊云開發者社區-騰訊云 (tencent.com)

2.2 線性回歸

線性回歸，顧名思義，其目標值（對應因變量）可以看作是各個特征值（對應自變量）的線性組合。

線性回歸模型的有效性建立在以下關鍵假設之上：

• 線性關系：因變量與自變量間存在線性關系。
• 獨立性：觀測值之間應相互獨立。
• 無多重共線性：模型中的任何一個自變量都不應該是其他自變量的精確線性組合。
• 同方差性：對于所有的觀測值，誤差項的方差應相等。
• 誤差項的正態分布：誤差項應呈正態分布。

上述假設確保了線性回歸模型能夠提供可靠的預測和推斷。

下圖列出的是與線性回歸相關的思維導圖。

2.2.1 經典線性回歸模型

（1）數學模型

經典的線性回歸數學模型可用下式描述：

這顯然是一條直線方程，其中，表示預測值，為系數，而為斜率。

這個模型的關鍵在于找到最適合數據的值，使得模型能夠準確預測因變量的值。

Sklearn使用LinearRegression函數完成線性模型的擬合。所使用的準則是“最小均方誤差”準則，即是使觀測數據與預測數據之間的均方誤差取得最小值，用數學表達式表示就是：

（2）數學模型

?在SKlearn中，使用LinearRegression函數實現線性回歸問題。

以下是該函數的聲明：

看一下LinearRegression函數的聲明：

sklearn.linear_model.LinearRegression(*, fit_intercept=True, copy_X=True, n_jobs=None, positive=False)

部分參數說明：

• fit_intercept：是否計算該模型的截距，默認為True。如果使用中心化的數據，可以考慮設置為False，即不計算截距。
• copy_X：是否對X進行復制，默認為True。如果設為False，在運行過程中新數據會覆蓋原數據。
• n_jobs：處理時設置任務個數，默認值為None。該參數對于目標個數大于1，且足夠大規模的問題有加速作用，如果設置為-1，則代表使用所有的CPU。
• positive：默認為False，如果設為Ture，則將各個系數強制設為正數。

屬性值：

• coef_：擬合得到的系數值。如果是單目標問題，返回一個以為數組；如果是多目標問題，返回一個二維數組。
• rank_：矩陣X的秩，僅X為稠密矩陣時有效。
• singular_：矩陣X的奇異值，僅X為稠密矩陣時有效。
• intercept_：截距，線性模型中的獨立項，如果fit_intercept設為False，則intercept_值為0。

該函數在使用時，調用了以下函數：

• fit：用于模型訓練
• get_params：獲取估計器的參數值
• set_params：設置估計器的參數
• predict：模型預測
• score：模型評估

（3）實例

本節將介紹如何使用LinearRegression函數實現對線性擬合的一個實例，該實例來自Sklearn官網，詳細介紹見代碼的注釋。

# Code source: Jaques Grobler
# License: BSD 3 clauseimport matplotlib.pyplot as plt
import numpy as npfrom sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score# Load the diabetes dataset
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)# Use only one feature
diabetes_X = diabetes_X[:, np.newaxis, 2]# Split the data into training/testing sets
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]# Split the targets into training/testing sets
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]# Create linear regression object
regr = linear_model.LinearRegression()# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)# The coefficients
print("Coefficients: \n", regr.coef_)
# The mean squared error
print("Mean squared error: %.2f" % mean_squared_error(diabetes_y_test, diabetes_y_pred))
# The coefficient of determination: 1 is perfect prediction
print("Coefficient of determination: %.2f" % r2_score(diabetes_y_test, diabetes_y_pred))# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test, color="black")
plt.plot(diabetes_X_test, diabetes_y_pred, color="blue", linewidth=3)plt.xticks(())
plt.yticks(())plt.show()

輸出結果為：

Coefficients: [938.23786125]
Mean squared error: 2548.07
Coefficient of determination: 0.47

下圖展示了擬合結果，其中黑色點代表測試數據點，藍線表示擬合出的直線。

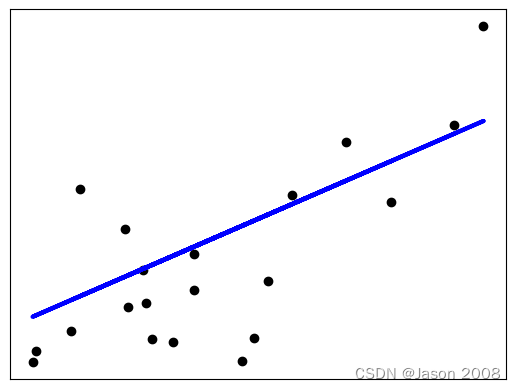
官網給出的實例，有些復雜。下面給出一個簡單直觀的例子。

sklearn——線性回歸與邏輯回歸_sklearn線性回歸-CSDN博客