Studying-代碼隨想錄訓練營day29| 134. 加油站、135. 分發糖果、860.檸檬水找零、406.根據身高重建隊列

第29天，貪心part03，快過半了(? ?_?)?💪，編程語言：C++

134.加油站

135. 分發糖果

860.檸檬水找零

406.根據身高重建隊列

134.加油站

文檔講解：代碼隨想錄加油站

視頻講解：手撕加油站

題目：

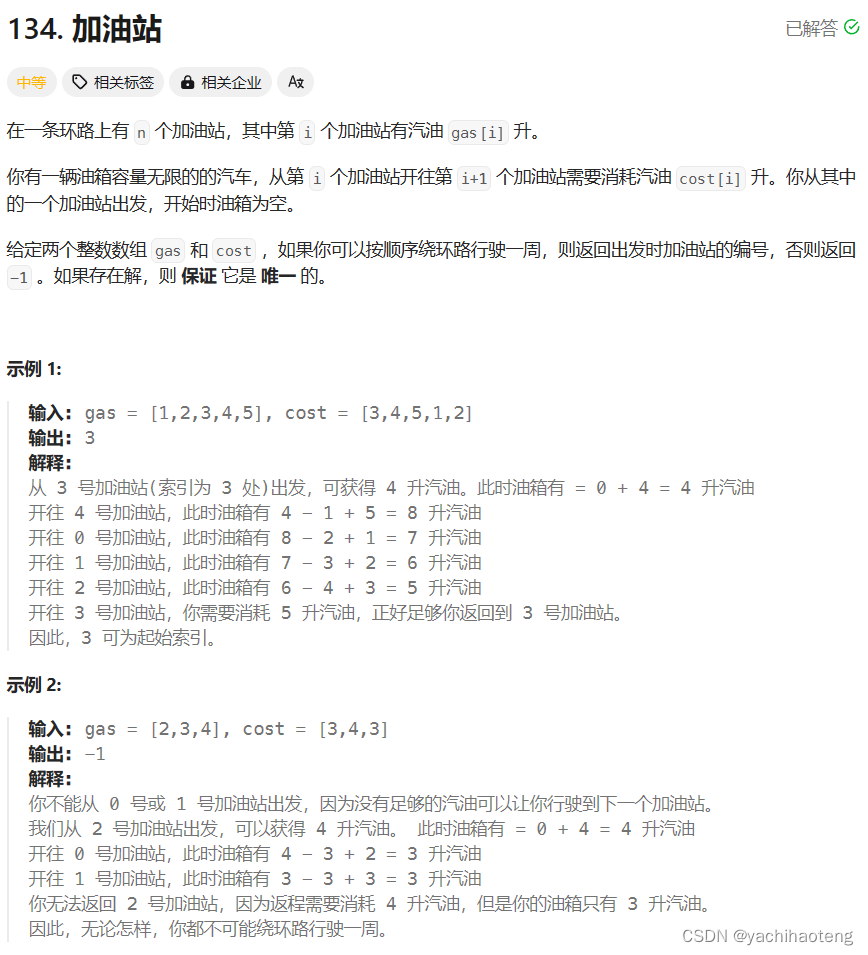
學習：本題其實很容易發現gas數組和cost數組的差，就是該站點結余的油量，我們在移動過程中理應讓油量始終保持為正。因此本題的思考邏輯就是從某個站點出發，如果油量小于0則說明該點不能環路行駛一圈，反則則可以。

解法一：暴力解法，暴力遍歷每個節點環行一周的結果。（力扣超時）

注意：for循環適合模擬從頭到尾的遍歷，而while循環適合模擬環形遍歷，因此對于本題的場景需要使用while進行環行循環要十分注意。

//時間復雜度O(n^2)
//空間復雜度O(1)
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {for (int i = 0; i < cost.size(); i++) {int rest = gas[i] - cost[i]; // 記錄剩余油量int index = (i + 1) % cost.size();while (rest > 0 && index != i) { // 模擬以i為起點行駛一圈（如果有rest==0，那么答案就不唯一了）rest += gas[index] - cost[index];index = (index + 1) % cost.size();}// 如果以i為起點跑一圈，剩余油量>=0，返回該起始位置if (rest >= 0 && index == i) return i;}return -1;}
};

解法二：貪心

貪心策略為：首先只有在總油量減去總消耗大于等于0的時候，才說明可以跑完一圈。其次我們在環行的過程中，還需要保持剩油量是正的，才能夠繼續行駛下去。因此我們可以 i 從0開始累加每個站點的剩油量(gas[i] - cost[i])，一旦累加和小于零，則說明[0, i]區間都不能作為起始位置，因為這個區間選擇任何一個位置作為起點，到i這里都會斷油（一定不會說從中間開始某個點不會斷油，因為如果是那樣的話后半部分為正，那前半部分一定為負，也會使得滿足剩油量為負的條件，跳到i+1），那么起始位置從i+1算起，再從0計算剩油量。

那么局部最優：當前累加rest[i]的和curSum一旦小于0，起始位置至少要是i+1，因為從i之前開始一定不行。全局最優：找到可以跑一圈的起始位置。

代碼：

//時間復雜度O(n)
//空間復雜度O(1)
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {//貪心，局部最優找到累加為正的地方int count = 0; //計算總和，總和小于0說明無法環路一周int idcount = 0; //計算當前i往后的總和，該總和小于0說明不能從i出發int index = 0; //找到正確的出發下標for(int i = 0; i < gas.size(); i++) {int rest = gas[i] - cost[i];count += rest;idcount += rest;if(idcount < 0) { // 當前累加rest[i]和 curSum一旦小于0idcount = 0;  // idcount從0開始計算index = i + 1;  //起始位置更新為i+1}}if(count < 0) return -1;return index;}
};

135. 分發糖果

文檔講解：代碼隨想錄分發糖果

視頻講解：手撕分發糖果

題目：

學習：本題屬于貪心算法中兩個維度的問題，也就是需要兩次貪心分別處理兩種情況。本題中我們對于一個孩子來說，即要考慮他的左邊和他的大小關系，又要考慮他的右邊和他的大小關系，這就是我們要處理的兩個問題。對于這種情況而言，我們需要將這兩個問題分開解決，先考慮每個孩子右邊比自身大的情況，再考慮每個孩子左邊比自身大的情況，不能同時考慮，否則就會顧此失彼。

首先考慮右邊孩子評分大的情況，從前向后遍歷。此時的局部最優為：只要右邊評分比左邊大，右邊的孩子就多一個糖果。全局最優為：相鄰的孩子中，評分高的右孩子獲得比左邊孩子更多的糖果。

接著我們再確定左邊孩子評分大的情況，從后往前遍歷。此時的局部最優就為：只要左邊評分比右邊大，左邊的孩子就多一個糖果。全局最優為：相鄰的孩子中，評分高的左孩子獲得比右邊孩子更多的糖果。（這個地方要注意，再更新評分更高的孩子的時候，我們要判斷此時更新的值和原本的值誰更大，因為原本的值是保證了他和他左邊孩子的關系，因為誰更大取誰，這樣就能夠同時保證左右孩子的關系了。

代碼：

//時間復雜度O(n)
//空間復雜度O(n)
class Solution {
public:int candy(vector<int>& ratings) {//兩次貪心vector<int> candys(ratings.size(), 1); //初始化先給每個小孩一個糖果//第一次貪心，從左向右，先遍歷右孩子比左孩子大的情況，局部最優：右孩子比左孩子大就多一個糖果for(int i = 1; i < ratings.size(); i++) {if(ratings[i] > ratings[i - 1]) {candys[i] = candys[i - 1] + 1;}}//第二次貪心，從右向左，遍歷左孩子比右孩子大的情況，局部最優：左孩子比右孩子大就多一個糖果for(int i = ratings.size() - 2; i >= 0; i--) {if (ratings[i] > ratings[i + 1]) {//這里要注意要去當前值和右孩子加1之間的最大值，這樣才能保證該點同時大于左右孩子。candys[i] = max(candys[i], candys[i + 1] + 1); }}//求和int result = 0;for(int i = 0; i < candys.size(); i++) {result += candys[i];}return result;}
};

860.檸檬水找零

文本講解：代碼隨想錄檸檬水找零

視頻講解：手撕檸檬水找零

題目：

學習：本題看起來題干很多很復雜，但實際上就是每位顧客花5美元買檸檬水，但這個過程中會出現三種情況分別是：1.顧客給了5美元，不需要找錢；2.顧客給了10美元，需要找5美元給顧客；3.顧客給了20美元，需要找15美元給顧客。針對這三種情況我們可以逐個分析。?

1.顧客給了5美元：對于這種情況，我們不需要找錢的同時，我們手里還多了一張5美元。

2.顧客給了10美元，需要找5美元：對于這種情況，需要我們手頭上有至少一張5美元，否則我們就不能正確找零返回false。如果我們手頭上有至少一張5美元，則我們減少一張5美元，多一張10美元。

3.顧客給了20美元，需要找15美元：對于這種情況，就是需要我們進行貪心算法的時候了，因為對于我們來說5美元既可以給10美元的顧客找錢，又可以給20美元的顧客找錢。因此我們在給20美元的顧客找錢的時候應優先消耗美元10，保留更加萬能的5美元，這樣才能更好的進行正確的找零。因此有三種情況：1.手頭上有10美元，5美元，則減少一張10美元，一張5美元；2.手頭上美元10美元，但5美元大于3張，則減少3張5美元；3.手頭上湊不出15美元的數（注意兩張10美元不行）返回false。

代碼：根據以上三種情況，則可編寫代碼

//時間復雜度O(n)
//空間復雜度O(1)
class Solution {
public:bool lemonadeChange(vector<int>& bills) {//記錄手頭上5美元和10美元的數量，20美元的不需要記錄，因為20沒有不能用于找錢int count5 = 0;int count10 = 0;for(int i = 0; i < bills.size(); i++) {//分別處理收到三種錢的情況if(bills[i] == 5) {count5++;}if(bills[i] == 10) {if(count5 == 0) {return false;}count5--;count10++;}//第三種情況需要進行貪心//貪心策略：如果有10元鈔票優先找10元鈔票，因為5元鈔票比10元鈔票更萬能if(bills[i] == 20) {if(count10 > 0 && count5 > 0) {count10--;count5--;}else if(count5 >= 3) {count5 -= 3;}else {return false;}}}return true;}
};

406.根據身高重建隊列

文檔講解：代碼隨想錄根據身高重建隊列

視頻講解：手撕根據身高重建隊列

題目：

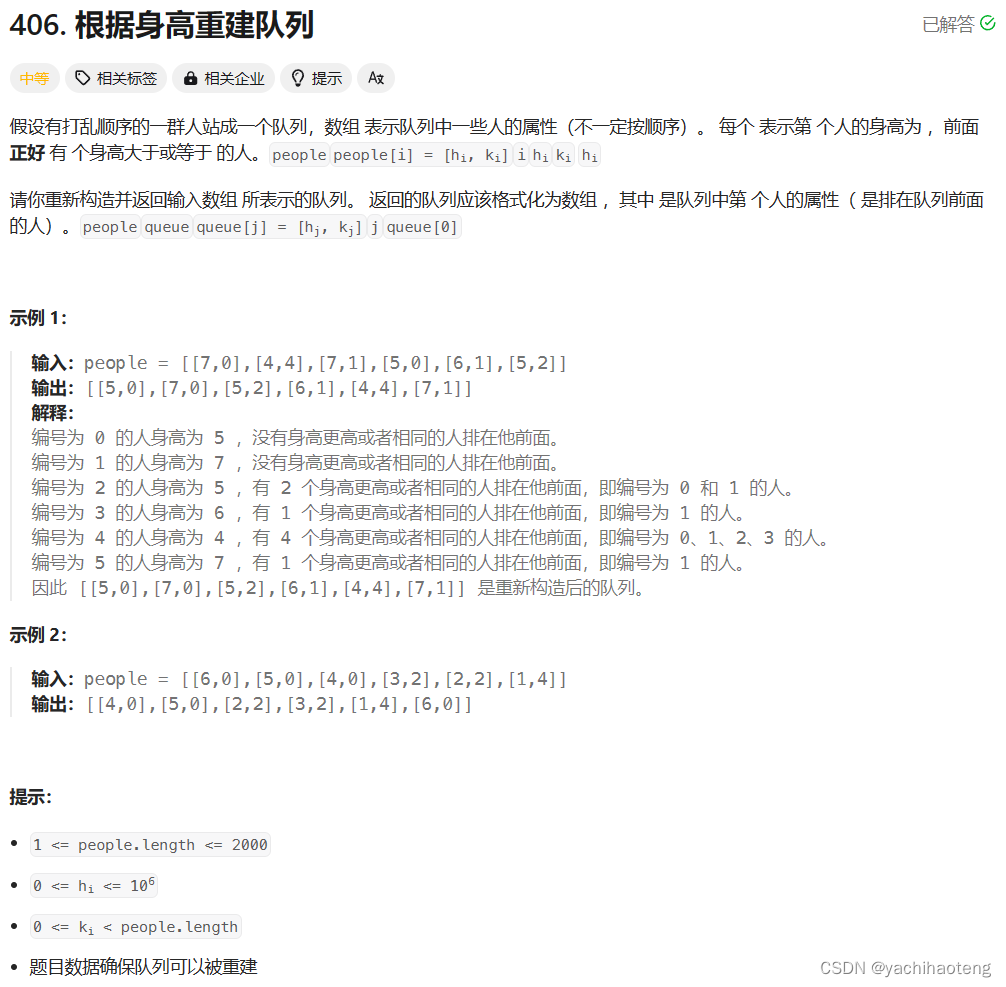
學習：本題與分發糖果相同，同樣都是兩維問題，我們需要分別考慮身高和前面身高大于等于的人的數量這兩個因素。不能兩個維度一起考慮，一定會出現顧此失彼的情況。

本題中如果我們需要對數組先進行排序，來解決一個維度上的問題。如果我們選擇對k(身高大于等于的數量）進行排序，會發現最后得到的數組會發現k的排列不符合條件，身高也不符合條件，兩個維度都沒辦法確定下來（這是因為會存在部分身高很高，因此k為0的干擾）。

因此本題我們需要先對身高進行排序，身高從高到低進行排序，這樣也會有個好處，排序之后，如果后面的位置出現問題需要前插，也不會影響前面的數的排序，因為后面的數一定比前面的數小，不會影響到k值。

因此本題的貪心就是：局部最優：優先按身高高的people的k來插入。插入操作過后的people滿足隊列屬性；全局最優：最后都做完插入操作，整個隊列滿足題目隊列屬性。

代碼：

//時間復雜度O(nlogn + n^2)
//空間復雜度O(n)
class Solution {
public:static bool camp(vector<int>&a, vector<int>&b) {//身高從大到小排列，便于進行插入處理if(a[0] != b[0]) {return a[0] > b[0];}else { //如果身高一樣，讓其前面身高少的排前面return a[1] < b[1];}}vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {//對數組進行排序，讓身高高的先排前面，這樣我們就能依據前面身高的數量，來插入每一個數sort(people.begin(), people.end(), camp);//貪心策略，遍歷數組，優先按照身高高的people的k來進行插入，這樣也就不用擔心后續身高矮的插入造成影響vector<vector<int>> queue; //這里不能初始化數組的大小，因為后續要采用插入進行操作for(int i = 0; i < people.size(); i++) {int index = people[i][1]; //確定要插入的位置queue.insert(queue.begin() + people[i][1], people[i]);}return queue;}
};

本題中存在一個問題，使用vector是非常費時的，C++中vector（可以理解是一個動態數組，底層是普通數組實現的）如果插入元素大于預先普通數組大小，vector底部會有一個擴容的操作，即申請兩倍于原先普通數組的大小，然后把數據拷貝到另一個更大的數組上。所以使用vector（動態數組）來insert，是費時的，插入再拷貝的話，單純一個插入的操作就是O(n^2)了，甚至可能拷貝好幾次，就不止O(n^2)了。

代碼：因此本題可以采用list類來保存數組，雖然時間復雜度沒變，但實際效率是增加了的。

class Solution {
public:// 身高從大到小排（身高相同k小的站前面）static bool cmp(const vector<int>& a, const vector<int>& b) {if (a[0] == b[0]) return a[1] < b[1];return a[0] > b[0];}vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {sort (people.begin(), people.end(), cmp);list<vector<int>> que; // list底層是鏈表實現，插入效率比vector高的多for (int i = 0; i < people.size(); i++) {int position = people[i][1]; // 插入到下標為position的位置std::list<vector<int>>::iterator it = que.begin();while (position--) { // 尋找在插入位置it++;}que.insert(it, people[i]);}return vector<vector<int>>(que.begin(), que.end());}
};