目錄

一、前言

二、如何區分【優先級隊列】與【隊列】？

三、priority_queue的介紹?

四、priority_queue 的構造?

五、priority_queue 的常用接口?

💧push

💧pop?

💧size??

💧top??

💧empty???

💧swap? ??

六、priority_queue 的模擬實現?

🥝 堆的向上調整算法

🥝 堆的向下調整算法

🥝 priority_queue 的實現

七、priority_ququq 中的仿函數?

八、priority_queue 的常考面試?

九、總結?

十、共勉?

---

一、前言

? ? ? ? 優先級隊列 priority_queue 是容器適配器中的一種，常用來進行對數據進行優先級處理，比如優先級高的值在前面，這其實就是數據結構中的 堆，它倆本質上是一樣東西，底層都是以數組存儲的完全二叉樹，不過優先級隊列 priority_queue 中加入了 泛型編程 的思想，并且屬于 STL 中的一部分。本就就來詳細的講解一下 priority_queue 是如何使用的！！

?二、如何區分【優先級隊列】與【隊列】？

首先要注意的就是別與 隊列（queue）搞混了，隊列是一種先進先出（First in First out，FIFO）的數據類型。每次元素的入隊都只能添加到隊列尾部，出隊時從隊列頭部開始出。

優先級隊列（priority_queue）其實，不滿足先進先出的條件，更像是數據類型中的“堆”。優先級隊列每次出隊的元素是隊列中優先級最高的那個元素，而不是隊首的元素。這個優先級可以通過元素的大小等進行定義。比如定義元素越大優先級越高，那么每次出隊，都是將當前隊列中最大的那個元素出隊。

三、priority_queue的介紹?

? ? ? ? priority_queue是C++標準庫中的一個容器適配器（container adapter），用于實現優先隊列（priority queue）的數據結構。優先隊列是一種特殊的隊列，其中的元素按照一定的優先級進行排序，每次取出的元素都是優先級最高的。它的底層實現通常使用堆（heap）數據結構。

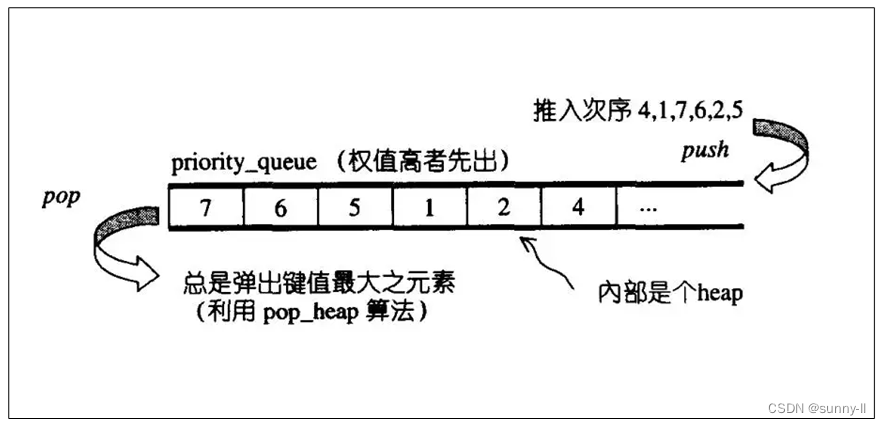
• 在C++中，priority_queue模板類定義在<queue>頭文件中，可以通過指定元素類型和比較函數來創建不同類型的優先隊列。比較函數用于確定元素的優先級，可以是函數指針、函數對象或Lambda表達式。
• ?priority_queue被實現為容器適配器，容器適配器即將特定容器類封裝作為其底層容器類。元素從特定容器的”尾部“彈出，其稱為優先級隊列的頂部

?需要注意的是，默認情況下，priority_queue使用std::less作為比較函數，即元素的優先級按照從大到小的順序排列。如果需要按照從小到大的順序排列，可以使用std::greater作為比較函數。?

四、priority_queue 的構造?

? ? ? ? 優先級隊列 默認使用 vector 作為底層存儲數據的容器，在 vector 上又使用了 堆算法 將 vector 中的元素構造成堆的結構，因此 priority_queue 就是 ---- 堆，所以在需要用到 堆 的地方，都可以考慮使用 priority_queue

注意：默認情況下 priority_queue 是 大堆

?優先級隊列的構造方式有兩種：直接構造一個空對象?和?通過迭代器區間進行構造

?（1）直接構造一個空對象

#include <iostream>
#include <vector>
#include <queue>	//注意：優先級隊列包含在 queue 的頭文件中using namespace std;int main()
{priority_queue<int> pq;	//直接構造一個空對象，默認為大堆cout << typeid(pq).name() << endl;	//查看類型return 0;
}

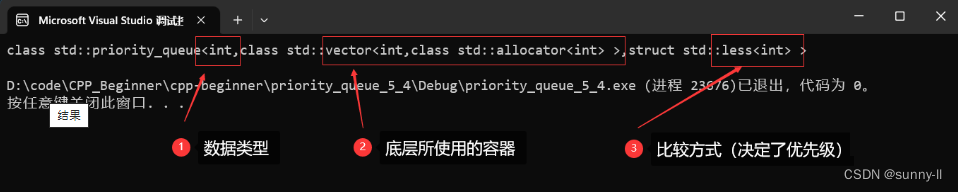
注意：?默認比較方式為?less，最終為 優先級高的值排在上面（大堆）

---

（2）通過迭代器區間構造對象?

#include <iostream>
#include <vector>
#include <queue>	//注意：優先級隊列包含在 queue 的頭文件中using namespace std;int main()
{vector<char> vc = { 'a','b','c','d','e' };priority_queue<char, deque<char>, greater<char>> pq(vc.begin(), vc.end());	//現在是小堆cout << typeid(pq).name() << endl;	//查看類型cout << "==========================" << endl;while (!pq.empty()){//將小堆中的堆頂元素，依次打印cout << pq.top() << " ";pq.pop();}return 0;
}

注意：?將比較方式改為?greater?后，生成的是?小堆，并且如果想修改比較方式的話，需要指明模板參數2?底層容器，因為比較方式位于模板參數3，不能跳躍缺省（遵循缺省參數規則）?

---

測試數據：【27,15,19,18,28,34,65,49,25,37】?分別生成 大堆 與 小堆?

大堆?：

vector<int> v = { 27,15,19,18,28,34,65,49,25,37 };
priority_queue<int, vector<int>, less<int>> pq(v.begin(), v.end());
//priority_queue<int> pq(v.begin(), v.end());	//兩種寫法結果是一樣的，默認為大堆

---

小堆：?

vector<int> v = { 27,15,19,18,28,34,65,49,25,37 };
priority_queue<int, vector<int>, greater<int>> pq(v.begin(), v.end());	//生成小堆

---

五、priority_queue 的常用接口?

優先級隊列的接口也很簡單，唯一需要注意的是，每插入一個元素，都會進行排序，主要看你構建的是大堆還是小堆。

💧push

在優先級隊列的尾部插入 一個 新的元素，每次插入前調用 堆排序算法，將其重新排序在堆中的位置?

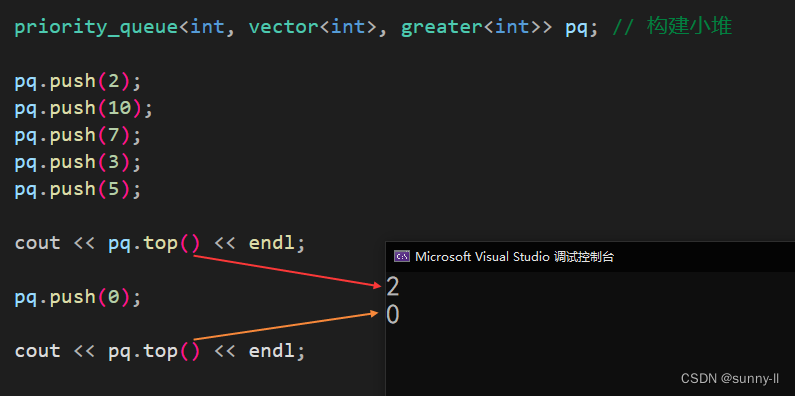
void test_priority_queue()
{priority_queue<int, vector<int>, greater<int>> pq; // 構建小堆pq.push(2);pq.push(10);pq.push(7);pq.push(3);pq.push(5);cout << pq.top() << endl;pq.push(0);cout << pq.top() << endl;
}

• 可以看到，我們構建的是小堆，排好序以后，隊頭（堆頂）的數據就是 2 ，重新插入一個 0 以后，會重新排序，此時隊頭（堆頂）的數據就是 0?

---

💧pop?

?刪除位于優先級隊列頂部的元素，有效的將其大小減少 1，其實就是刪除隊頭元素

void test_priority_queue()
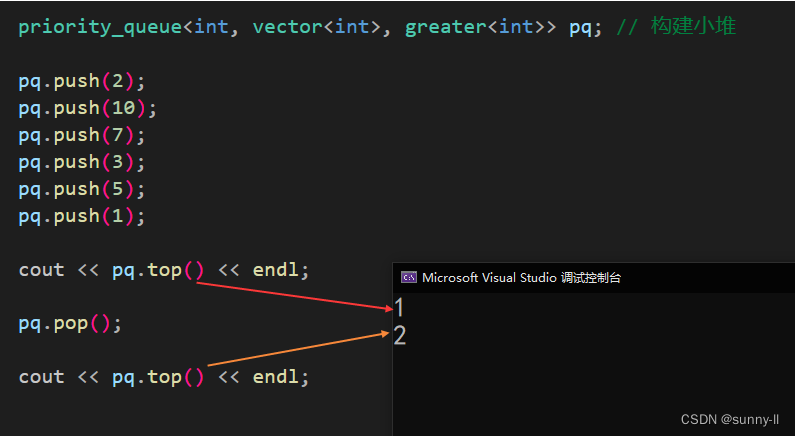
{priority_queue<int, vector<int>, greater<int>> pq; // 構建小堆pq.push(2);pq.push(10);pq.push(7);pq.push(3);pq.push(5);pq.push(1);cout << pq.top() << endl;pq.pop();cout << pq.top() << endl;
}

---

💧size??

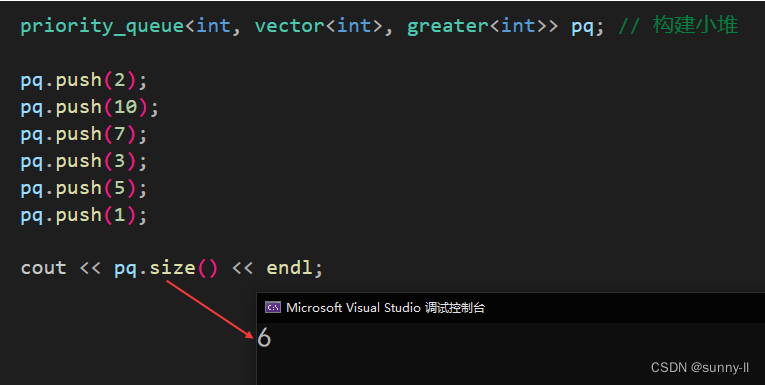
返回優先級隊列的元素數量?

void test_priority_queue()
{priority_queue<int, vector<int>, greater<int>> pq; // 構建小堆pq.push(2);pq.push(10);pq.push(7);pq.push(3);pq.push(5);pq.push(1);cout << pq.size() << endl;}

---

💧top??

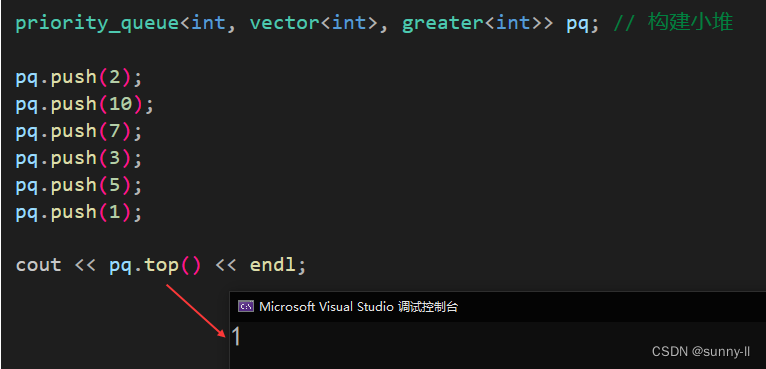
返回 優先級隊列中頂部元素的常量引用，頂部元素實在優先級隊列中比較高的元素?

void test_priority_queue()
{priority_queue<int, vector<int>, greater<int>> pq; // 構建小堆pq.push(2);pq.push(10);pq.push(7);pq.push(3);pq.push(5);pq.push(1);cout << pq.top() << endl;
}

---

💧empty???

?測試容器是否為空

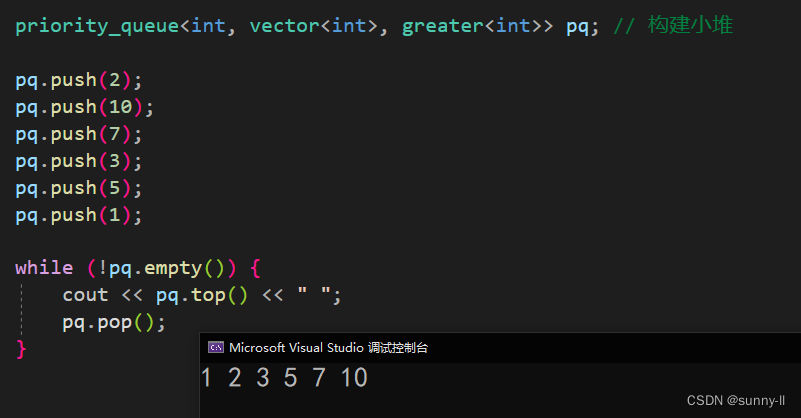
優先級隊列同樣也不支持迭代器的遍歷，所以可以使用 empty 配合 top 和 pop 來實現?

void test_priority_queue()
{priority_queue<int, vector<int>, greater<int>> pq; // 構建小堆pq.push(2);pq.push(10);pq.push(7);pq.push(3);pq.push(5);pq.push(1);while (!pq.empty()) {cout << pq.top() << " ";pq.pop();}
}

---

💧swap? ??

交換兩個優先級隊列的內容

void test_priority_queue()
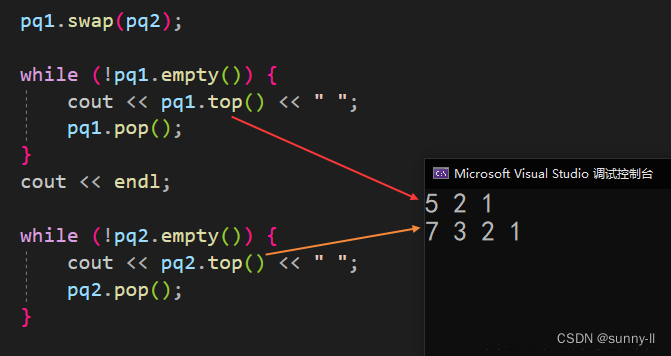
{priority_queue<int> pq1; // 構建小堆pq1.push(2);pq1.push(1);pq1.push(7);pq1.push(3);priority_queue<int> pq2;pq2.push(5);pq2.push(1);pq2.push(2);pq1.swap(pq2);while (!pq1.empty()) {cout << pq1.top() << " ";pq1.pop();}cout << endl;while (!pq2.empty()) {cout << pq2.top() << " ";pq2.pop();}
}

?注意：交換的前提必須是 兩個隊列構建都是相同的類型的堆

---

六、priority_queue 的模擬實現?

我們知道「priority_ queue」 的底層就是堆，所以在模擬實現之前，要先實現堆的調整算法。?

🥝 堆的向上調整算法

假設我們現在已經有一個大堆， 我們需要在堆的末尾插入數據，然后對其進行調整，使其仍然保持大堆的結構。

堆的向上調整算法基本思想: (以建 大堆為例)?

• 將要插入的數據與其父節點數據比較?
• 若插入節點的數據大于父節點的數據，則交換位置,交換以后，插入的節點繼續進行向上調整(此時該節點叔和上面的父節點比

來看一個動圖 :?

• (1) 首先我們在該大堆的末尾插入數據 60。?
• (2) 我們先將 60 與其父結點 27 進行比較,發現 60 比其父結點大，則交換父子結點的數據，并繼續進行向.上調整。
• (3) 此時將 60 與其父結點 28 進行比較，發現 60 還是比父結點大，則繼續交換父子結點的數據，并繼續進行向上調整。
• (4) 這時再將 60 與其父結點 65 進行比較,發現 60 比其父結點小，則停止向上調整,此時該樹已經就是大堆了。

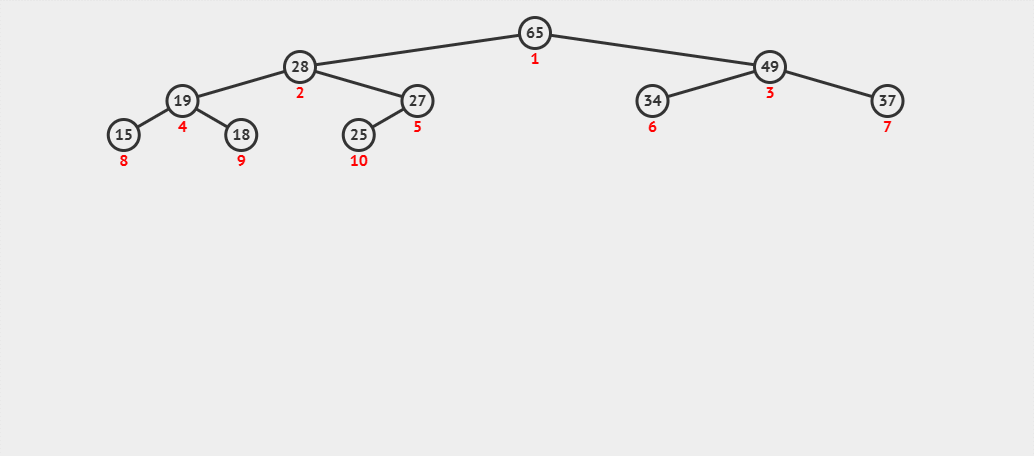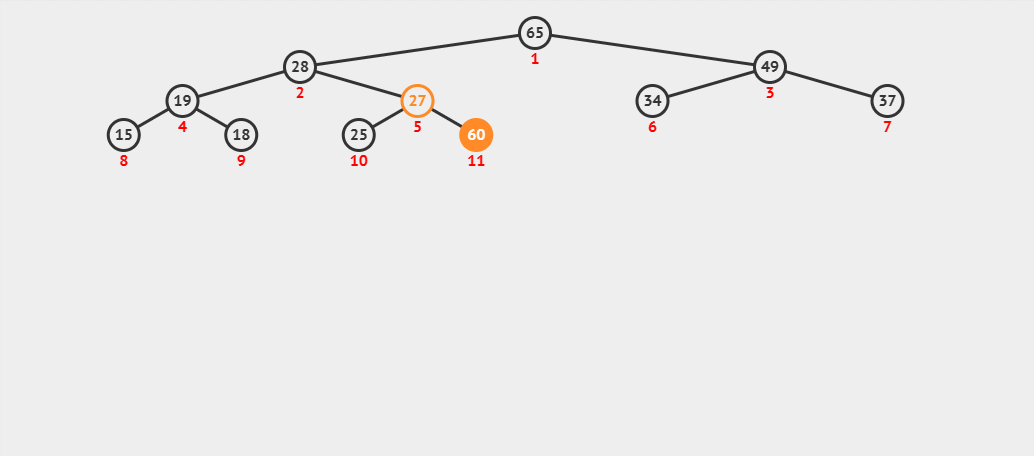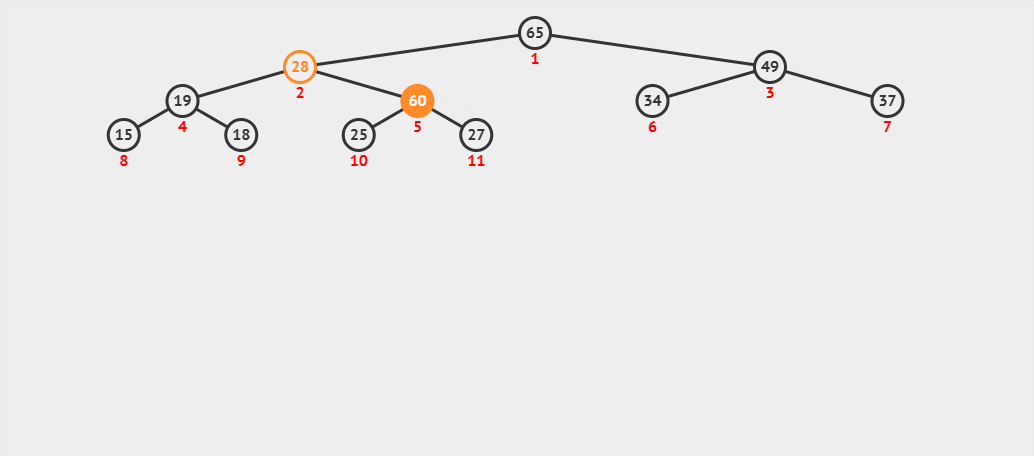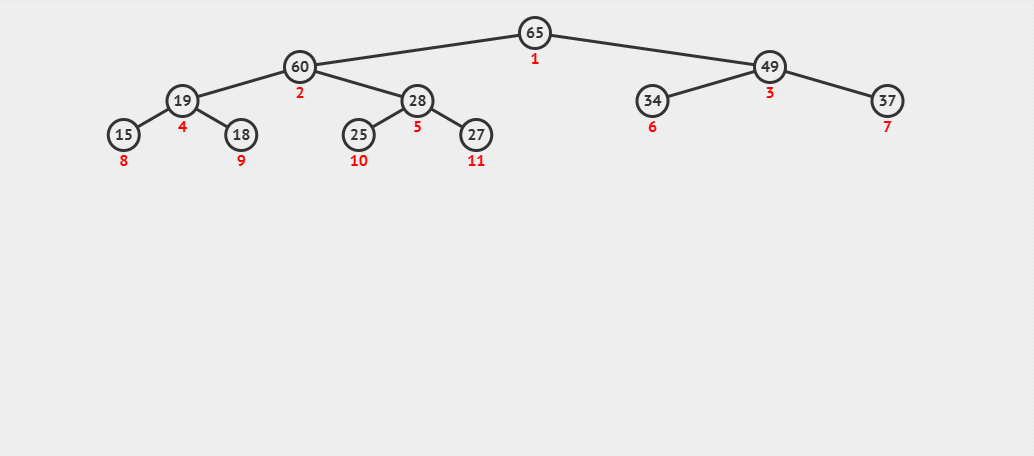
堆 的向上調整代碼：?

void AdjustUp(vector<int>& v1, int child)
{int parent = ((child - 1) >> 1); // 通過child計算parent的下標while (child > 0) //調整到根結點的位置截止{if (v1[parent] < v1[parent]){// 父節點與子節點交換swap(v1[child], v1[parent]);// 繼續向上調整child = parent;parent = ((child - 1) >> 1);}else {break;}}
}

---

🥝 堆的向下調整算法

以小堆為例，向下調整算法有一個前提，就是待向下調整的結點的左子樹和右子樹必須都為小堆?

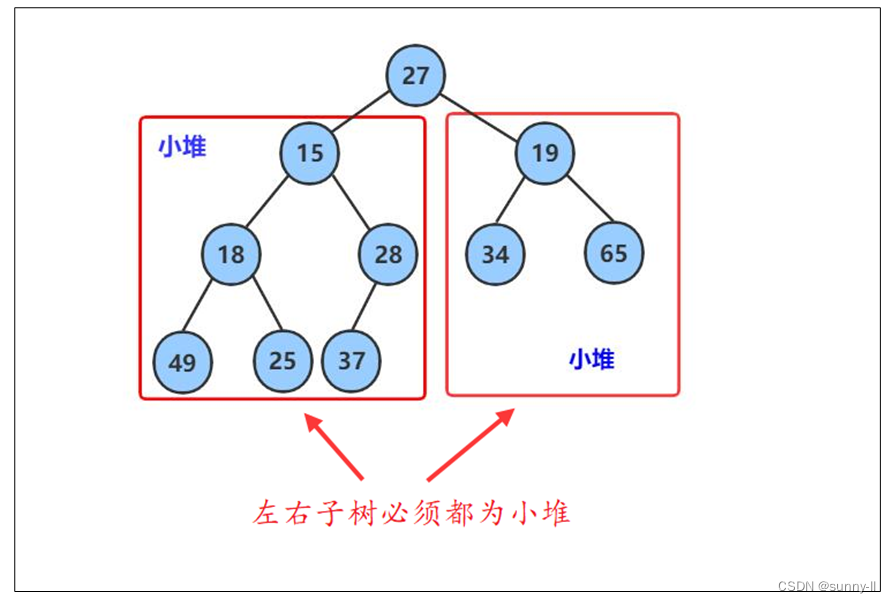
?堆的向下調整算法基本思想: (以建小堆為例)

• 從根節點開始，選出左右孩子節點中值較小的一個,讓父親與較小的孩子比較。?
• 若父親大于此孩子那么交換，交換以后,繼續進行向下調整;若父親小于此孩子，則不交換，停止向下調整，此時該樹已經是小堆

如下圖所示:將該二叉樹從根結點開始進行向下調整。(此時根結點的左右子樹已經是小堆)

將 27 與其較小的子結點 15 進行比較，發現 25 其較小的子結點大，則交換這兩個結點的數據，并繼續進行向下調整。?

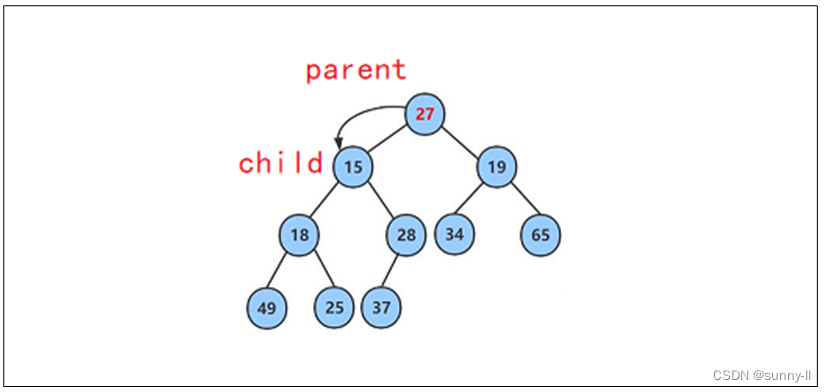
此時再將27與其較小的子結點18進行比較,發現27其較大的子結點大，則再交換這兩個結點的數據，并繼續進行向下調整。?

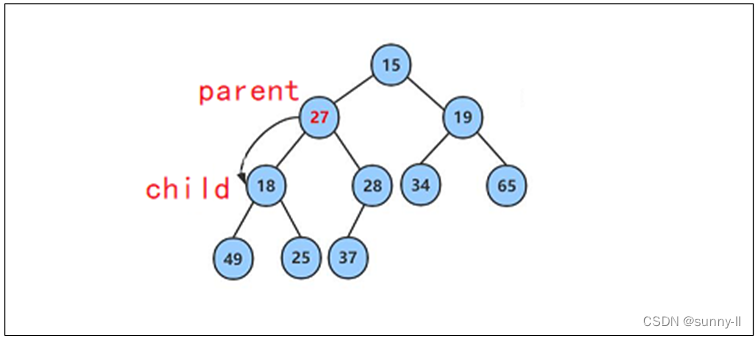
此時再將27與其較小的子結點25進行比較,發現27其較小的子結點大，則再交換這兩個結點的數據，并繼續進行向下調整。

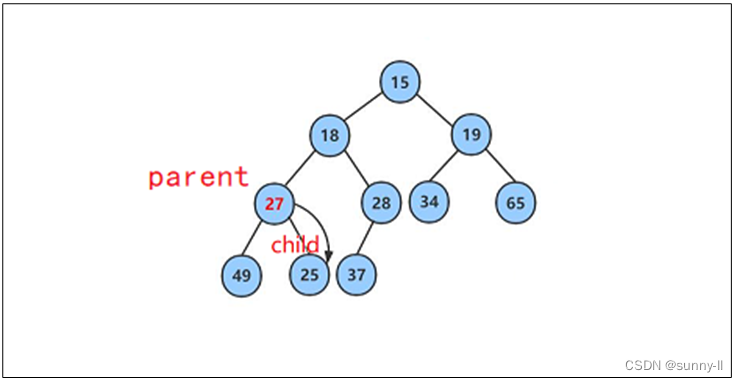
此時該樹，就因該是小堆啦?

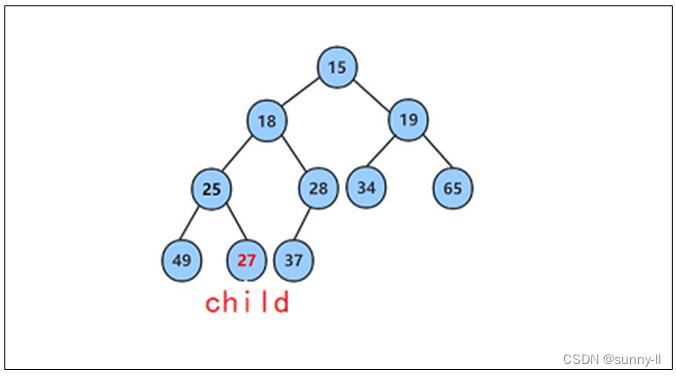
堆的向下調整代碼：?

//堆的向下調整（小堆）
void AdjustDown(vector<int>& v1, int n, int parent)
{//child記錄左右孩子中值較大的孩子的下標int child = 2 * parent + 1;//先默認其左孩子的值較小while (child < n){if (child + 1 < n && v1[child + 1] < v1[child])//右孩子存在并且右孩子比左孩子小{child++;//較小的孩子改為右孩子}if (v1[child] < v1[parent])//左右孩子中較小孩子的值比父結點還小{//將父結點與較小的子結點交換swap(v1[child], v1[parent]);//繼續向下進行調整parent = child;child = 2 * parent + 1;}else{break;}}
}

---

🥝 priority_queue 的實現

通過對「priority_ _queue」 的了 解其底層結構就是堆，此處只需對堆的調整算法和常用接口進行通用的封裝即可。?

namespace xas
{// 比較方式（使內部結構為大堆）template<class T>struct less{bool operator()(const T& x, const T& y) const{return x < y;}};// 比較方式（使內部結構為小堆）template<class T>struct greater{bool operator()(const T& x, const T& y) const{return x > y;}};// 優先級隊列 --- 大堆 < --- 小堆 >template<class T, class Container = vector<T>, class Compare = less<T>>class priority_queue{Compare _comFunc; // 比較方式public:// 創造空的優先級隊列priority_queue(const Compare& comFunc = Compare()):_comFunc(comFunc){}// 以迭代器區間來建堆template <class InputIterator>priority_queue(InputIterator first, InputIterator last, const Compare& comFunc = Compare()): _comFunc(comFunc){while (first != last){_con.push_back(*first);++first;}// 建堆for (int i = (_con.size() - 1 - 1) / 2; i >= 0; --i){AdjustDown(i);}}// 堆的向上調整void AdjustUp(int child){int parent = (child - 1) / 2; // 通過child計算parent的下標while (child > 0){if (_comFunc(_con[parent], _con[child])) // 通過所給比較方式確定是否需要交換結點位置{swap(_con[parent], _con[child]); // 將父結點與孩子結點交換child = parent; //繼續向上進行調整parent = (child - 1) / 2;}else{break;}}}// 插入元素到隊尾（并排序）// 在容器尾部插入元素后進行一次向上調整算法void push(const T& x){_con.push_back(x);AdjustUp(_con.size() - 1);}// 堆的向下調整void AdjustDown(int parent){size_t child = parent * 2 + 1;while (child < _con.size()){if (child + 1 < _con.size() && _comFunc(_con[child], _con[child + 1])){++child;}if (_comFunc(_con[parent], _con[child])) //通過所給比較方式確定是否需要交換結點位置{swap(_con[parent], _con[child]); //將父結點與孩子結點交換parent = child; //繼續向下進行調整child = parent * 2 + 1;}else{break;}}}// 刪除隊頭元素（堆頂元素）// 將容器頭部和尾部元素交換，再將尾部元素刪除，最后從根結點開始進行一次向下調整算法void pop(){assert(!_con.empty());swap(_con[0], _con[_con.size() - 1]);_con.pop_back();AdjustDown(0);}// 訪問隊頭元素（堆頂元素）const T& top(){return _con[0];}// 獲取隊列中有效元素個數size_t size(){return _con.size();}// 判斷隊列是否為空bool empty(){return _con.empty();}private:Container _con;};// 測試函數void test_priority_queue1(){priority_queue<int> pq1; // 構建大堆pq1.push(2);pq1.push(1);pq1.push(7);pq1.push(5);pq1.push(3);pq1.push(10);pq1.push(4);while (!pq1.empty()) {cout << pq1.top() << " ";pq1.pop();}}// 測試函數void test_priority_queue2(){priority_queue<int, vector<int>, greater<int>> pq2; // 構建小堆pq2.push(2);pq2.push(1);pq2.push(7);pq2.push(5);pq2.push(3);pq2.push(10);pq2.push(4);while (!pq2.empty()) {cout << pq2.top() << " ";pq2.pop();}}
}

七、priority_ququq 中的仿函數?

? ? ? ? 在priority_queue中，仿函數用于比較元素的優先級，并根據其返回值確定它們在隊列中的位置。默認情況下，priority_queue使用std::less作為仿函數，也就是將元素按照從大到小的順序進行排序。?

你可以使用不同的仿函數來改變元素的排序方式。以下是一些常見的仿函數：?

• std::less<T>：對于基本數據類型和自定義類型，默認使用?<?運算符進行比較，按照從大到小的順序排序。
• std::greater<T>：對于基本數據類型和自定義類型，默認使用?>?運算符進行比較，按照從小到大的順序排序。

除了上述默認提供的仿函數外，你還可以自定義仿函數來實現自定義的元素比較規則。自定義仿函數需要滿足嚴格弱排序（Strict Weak Ordering）的要求，即：?

• 比較關系必須是可傳遞的（transitive）：對于任意元素a、b和c，如果a與b比較相等，b與c比較相等，則a與c比較也相等。
• 比較關系不能是部分順序（partial order）：對于任意元素a和b，它們不能同時大于、小于或等于彼此。
• 比較關系必須是可比較的（comparable）：比較關系的結果必須對所有元素定義明確的大小關系。

以下這段代碼，演示了如何自定義一個仿函數來實現元素的自定義排序方式：?

// 創建一個 身份結構體
struct Person
{string name;int age;// 構造函數Person(const string& n, int a):name(n), age(a){}
};// 自定義仿函數
struct Compare
{// 函數重載()bool operator()(const Person& p1, const Person& p2)const{//按照年齡從下到大排序return p1.age > p2.age;}
};int main()
{priority_queue<Person, vector<Person>, Compare> pq;pq.push(Person("Alice", 25));pq.push(Person("Bob", 30));pq.push(Person("Charlie", 20));while (!pq.empty()) {Person p = pq.top();pq.pop();cout << p.name << " - " << p.age << endl;}return 0;
}

輸出結果為：?

Charlie - 20
Alice - 25
Bob - 30

在上面的代碼中，我們定義了一個名為Compare的結構體，重載了函數調用運算符operator()，按照Person對象的age成員進行比較。然后，我們將Compare作為優先隊列的仿函數類型，并插入3個Person對象到優先隊列中。最后，我們按照自定義的排序方式依次取出元素并輸出。?

---

八、priority_queue 的常考面試?

優先級隊列（堆）可以用來進行排序和解決?Top-K?問題，比如?查找第 k 個最大的值?就比較適合使用優先級隊列?

215. 數組中的第K個最大元素 - 力扣（LeetCode）?

思路：利用數組建立大堆，數組從大到小排序，刪除前k-1個元素，選出隊頭即可

class Solution {
public:int findKthLargest(vector<int>& nums, int k) {// 將數組中的元素 放入 優先級隊列--堆priority_queue<int> p(nums.begin(),nums.end());// 將優先級隊列 中的前K-1 個元素刪除掉for(int i = 0;i< k-1;i++){p.pop();}return p.top();}
};

---

?九、總結?

優先隊列是一種特殊的隊列，其中存儲的元素按照一定的優先級進行排列。在priority_queue中，優先級最高的元素能夠快速被訪問和刪除。

• 首先，我們介紹了priority_queue的概念和特點。它是基于堆（heap）這種數據結構實現的，通常使用最大堆來進行內部排序。最大堆保證了根節點的值最大，并且任意節點的值大于或等于其子節點的值。這種特性使得優先隊列能夠高效地訪問和刪除具有最高優先級的元素。
• 接著，我們深入探討了priority_queue的使用方法。基本操作包括插入元素、刪除元素、訪問元素和檢查隊列是否為空。
• 底層結構是priority_queue的關鍵部分，它通常使用堆來實現。在堆中，通過使用數組的索引來表示節點之間的關系，能夠快速定位和操作元素。
• 最后，我們探討了在priority_queue中使用的仿函數。仿函數用于確定元素之間的優先級，決定元素在隊列中的位置。默認情況下，priority_queue使用std::less仿函數進行比較，對元素進行降序排列。你還可以選擇其他仿函數或自定義仿函數來實現不同的排序方式。

---

十、共勉?

? ? ??以下就是我對 【priority_queue優先級隊列】?的理解，如果有不懂和發現問題的小伙伴，請在評論區說出來哦，同時我還會繼續更新對?C++STL?的理解，請持續關注我哦！！！???