---

---

圖

圖的知識盤點

pathfinding

作為一名計算機專業的學生，對于圖這種數據結構也是爛熟于心了。圖是一種包含了多個結點的數據結構，它是結點和路徑的集合。可以用鄰接表和鄰接矩陣來表示一張圖。

圖的表示可以通過計算得到結點之間的可達和不可達，耗費的代價等等。在許多數學問題上十分有用。通常解決圖問題的算法被我們稱為尋路算法。

尋路算法

在大學期間，我們就學習過一些基本的尋路算法：

BFS廣度優先算法

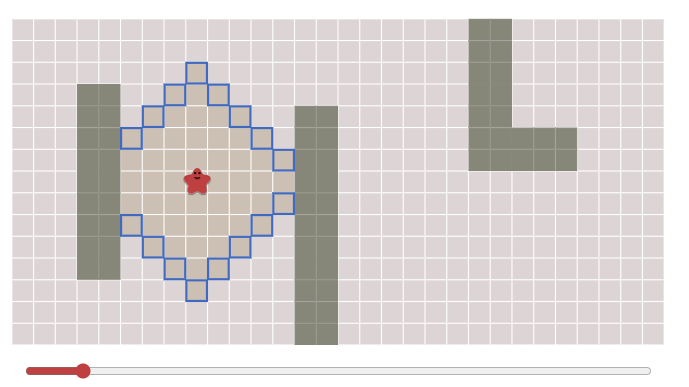
廣度優先算法的原理是，以起始點為中心，向四周的相鄰點（也就是與當前點連通且路長為1的那些節點）依次遍歷。當遍歷完相鄰節點后，再遍歷相鄰結點的相鄰點，依次類推。

當找到結束點后，只需要從終點開始，反向按著相鄰節點的最小遍歷序號數尋找，就能找到最短路徑了

DFS深度優先

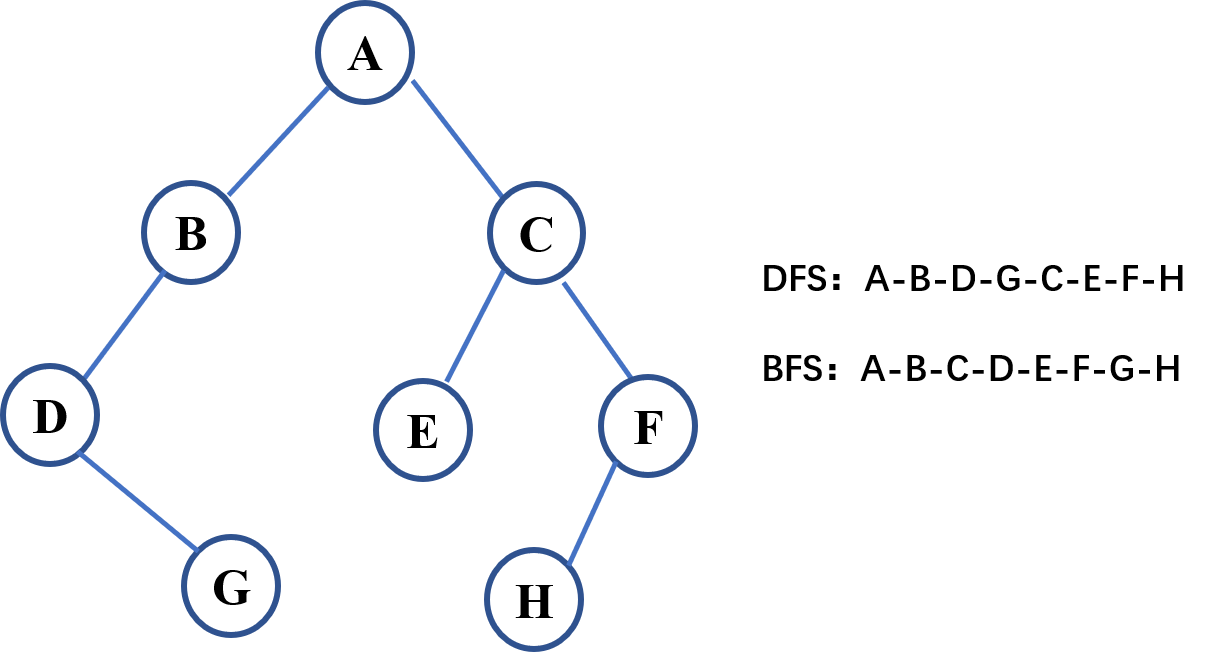
如果說廣度優先是以中心向四周擴散的圓形方式尋找，深度優先就是一條線的一直找下去。深度優先不斷的尋找未經過的相鄰節點，直到不再有可遍歷的相鄰節點才會考慮回退到上一個節點并再換一個方向找。

深度優先算法其實更適合在樹種的查找，而在圖中特別是當一些圖的節點是全連通的時候，深度優先就很難用了。

貪心算法

貪心算法適用于路徑帶有不同權值的時候，遍歷時我們優先遍歷相鄰結點中權值較小者，這樣做的好處是如果找到了路徑，那么我們的路徑一定是部分最短的（相鄰結點永遠是最短的，雖然不一定是全局最短，但是相對來說不會是最差的）

---

引入權重

現在我們要為尋路算法引入權重值，每個結點的權重值不一樣，權重值由起點和終點的距離決定，權重越小則距離越小。

Dijkstra算法

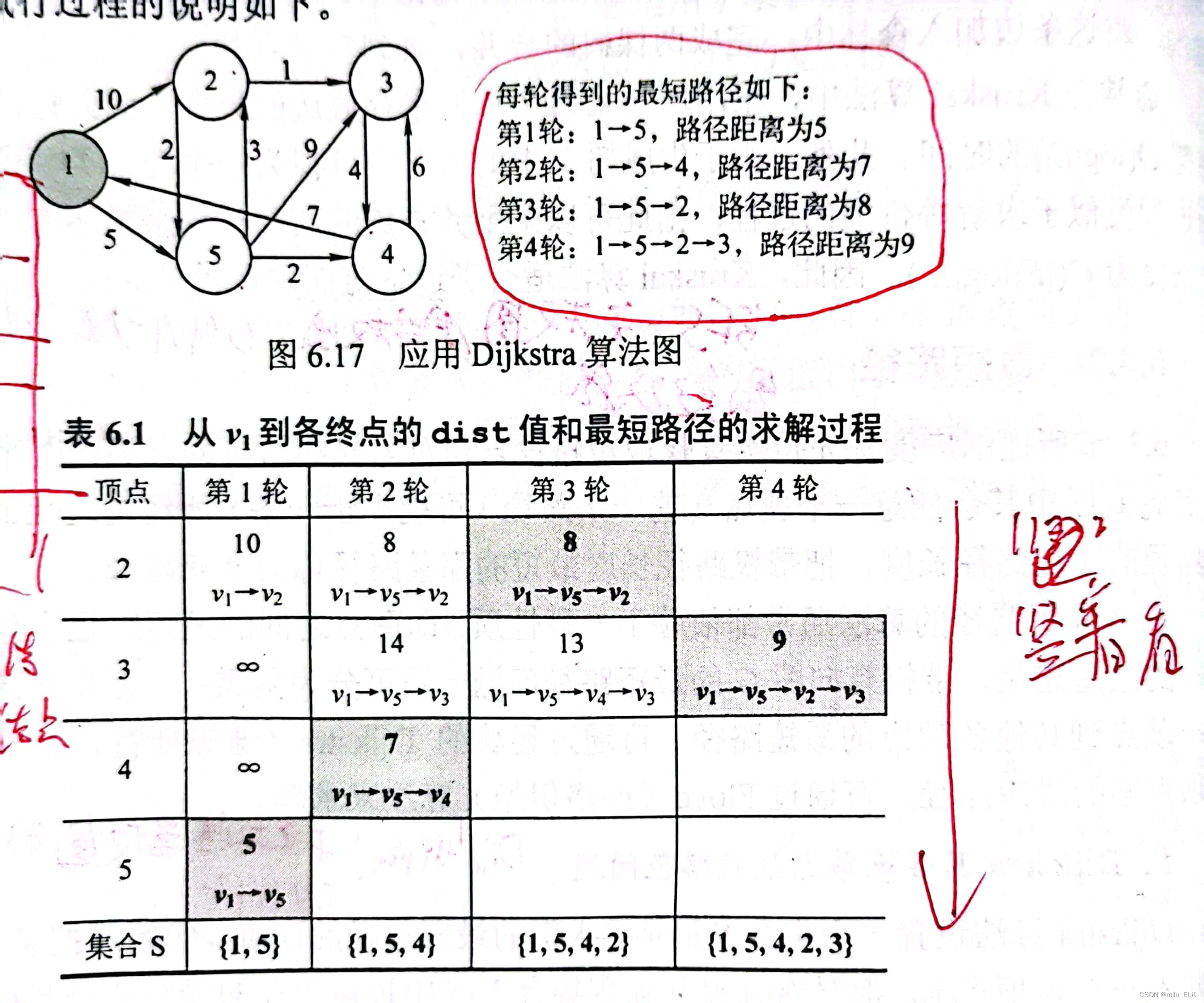
Dijkstra算法的原理是先算出起始點到其他點的最短路徑，再求解。

例如以上圖點1到點3為例，第一輪中找到點1到相鄰點的最短路徑是v1-v5，cost為5。那么我們就按著這個最短路徑走，接著第二輪從點v5開始計算v5到其他點的路徑長度。依次類推，按照表格上的路徑，在第二輪發現v4達到不了v3，因此我們放棄這條路徑，再次回到第二輪，選擇除了這條路徑以外最短的，也就是v1-v5-v2，按照這條路徑走發現是可以到達v3的，此時就是我們的最短路徑。

當找不到最短路徑時，就要回退到本輪的第二短，本輪第二短達不到就第三短…以此類推。若本輪所有路徑都不可達，那就回退到上一輪，選擇上一輪中未選擇的路徑。

當圖為網格圖，且每個結點之間的移動代價相等時，Dijkstra就等于廣度優先

---

現在讓我們引入權值計算公式：默認權值為起點和終點間的距離
$abs(start.x?end.x)+abs(start.y?end.y)$

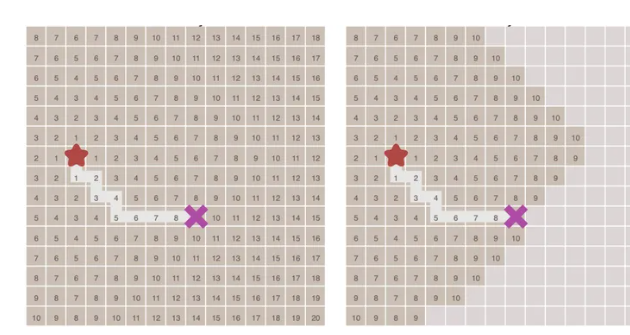
對比Dijkstra算法和貪心算法，在簡單的情況下貪心算法更有優勢：

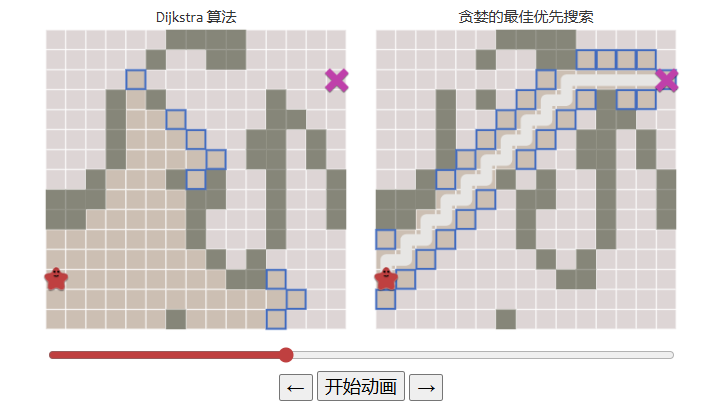
而一旦出現了復雜的地形，貪心算法就不一定是有效的了：

---

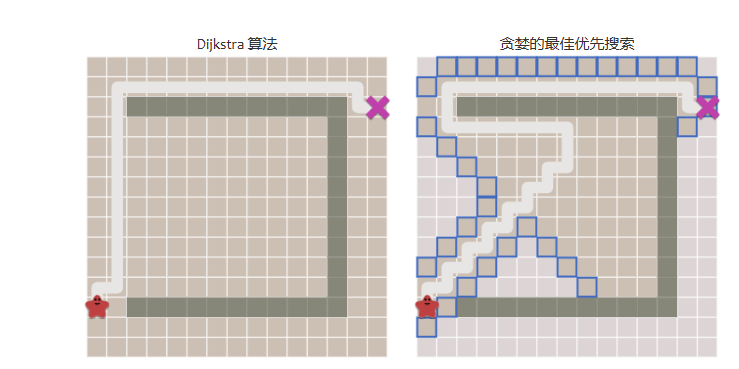
A*算法

之前講了這么多，介紹了一些常見的尋路算法。Dijkstra效果好但是可能造成時間上的浪費，貪心算法速度快，但是最終的結果不一定是最短路徑。

因此我們要學習A*算法：

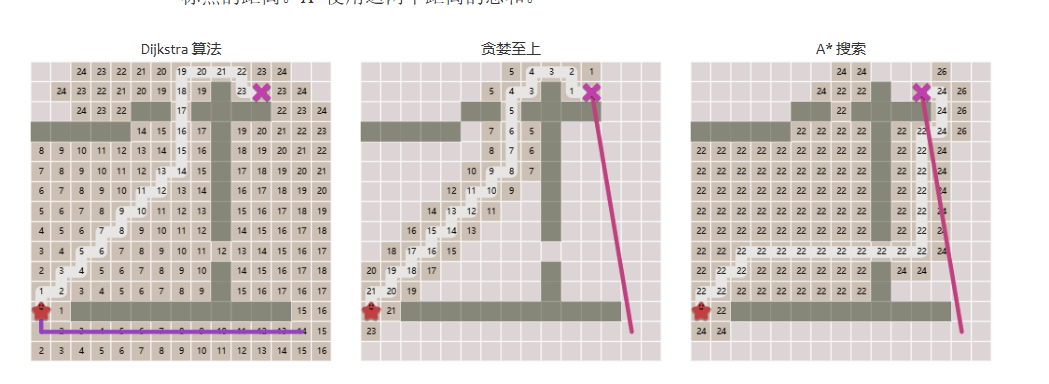
在A*算法下，找到的路徑長度將是最短的，且用時要比Dijkstra算法要小。

A*算法是一種啟發式算法，它通過這個函數來計算每個結點的優先級：

$f(n)=g(n)+h(n)$

其中

• f(n)是節點n的綜合優先級。當我們選擇下一個要遍歷的節點時，我們總會選取綜合優先級最高（值最小）的節點。
• g(n) 是節點n距離起點的代價。
• h(n)是節點n距離終點的預計代價，這也就是A*算法的啟發函數。關于啟發函數我們在下面詳細講解。

A*算法在運算過程中，每次從優先隊列中選取f(n)值最小（優先級最高）的結點作為下一個待遍歷的節點。而不是類似Dijkstra算法，每次遍歷相鄰結點時盡管下一個結點可能出現權值過大的情況，但是我們不能確保它不是全局最優的，因此我們依然要把它加入到遍歷路徑中。

而相比下貪心算法雖然局部最優，但也不能確保是全局最優解。

A*算法的高明之處在于，除了實際代價，還有預估代價作為參考，當遍歷結點越接近終點，則$g(n)越大，h(n)越小$,因此往往在最短路徑上的結點值$f(n)$相差不大。因此我們可以用貪心算法選取優先路徑，再用Dijkstra進行遍歷。遍歷的節點數量也小于Dijkstra算法 。

如果選取的啟發函數有問題，那么結果可能更偏向Dijkstra算法。

---

C#實現

版權聲明：本文為博主原創文章，遵循 CC 4.0 BY-SA 版權協議，轉載請附上原文出處鏈接和本聲明。
原文鏈接：https://blog.csdn.net/qq_60125117/article/details/130233023

轉自C# A*算法，總結的太好了，我就直接抄了

A*算法使用一個開放列表(open list)和一個封閉列表(closed list)來維護搜索過程。開放列表存儲待擴展的節點，而封閉列表存儲已經擴展過的節點，以避免重復擴展節點。

在搜索過程中，我們從開放列表中選擇f值最小的節點進行擴展，并將其加入封閉列表中。如果該節點是目標狀態，則搜索結束，并返回從起點到目標狀態的最短路徑。

步驟

1. 將起點加入開放列表，并將其代價設置為0。
2. 從開放列表中選擇代價$f(n)$值最小的節點進行擴展，即優先選擇離目標狀態更接近的節點。
3. 將該節點從開放列表中移除，并加入封閉列表中。
4. 對該節點的所有相鄰節點進行以下操作：
   1. 如果該節點已經在封閉列表中，則忽略該節點
   2. 如果該節點不在開放列表中，則將其加入開放列表，并將其代價和父節點設置為當前節點
   3. 如果該節點已經在開放列表中，則比較當前節點到該節點的代價和已有的代價，選擇代價較小的路徑，并更新該節點的代價和父節點。
5. 重復步驟2-4，直到開放列表為空或找到目標狀態。
6. 如果找到目標狀態，則從目標狀態開始回溯路徑，直到回溯到初始狀態。

public List<Node> FindPath(Node start, Node end)
{// 存儲已訪問的節點var closedSet = new HashSet<Node>();// 存儲待訪問的節點var openSet = new Heap<Node>(nodeComparer);openSet.Add(start);// 存儲節點到起點的實際代價var gScore = new Dictionary<Node, float>();gScore[start] = 0;// 存儲節點到終點的估計代價var hScore = new Dictionary<Node, float>();hScore[start] = HeuristicCostEstimate(start, end);// 存儲每個節點的父節點，用于回溯路徑var cameFrom = new Dictionary<Node, Node>();while (openSet.Count > 0){// 獲取最小估價的節點var current = openSet.RemoveFirst();if (current == end){// 找到目標狀態，回溯路徑var path = new List<Node>();while (current != start){path.Add(current);current = cameFrom[current];}path.Reverse();return path;}// 標記當前節點已訪問closedSet.Add(current);// 遍歷當前節點的相鄰節點foreach (var neighbor in current.Neighbors){if (closedSet.Contains(neighbor))continue; // 相鄰節點已經訪問過了// 計算當前節點到相鄰節點的實際代價// 關于代價函數t(n)=g(n)+h(n)，其中啟發函數h(n)是可以自定義的，只要效果好就行var tentativeGScore = gScore[current] + DistanceBetween(current, neighbor);// 如果相鄰節點不在待訪問列表中，或者到相鄰節點的代價更小if (!openSet.Contains(neighbor) || tentativeGScore < gScore[neighbor]){// 更新相鄰節點的父節點和代價cameFrom[neighbor] = current;gScore[neighbor] = tentativeGScore;hScore[neighbor] = HeuristicCostEstimate(neighbor, end);// 如果相鄰節點不在待訪問列表中，加入待訪問列表if (!openSet.Contains(neighbor))openSet.Add(neighbor);}}}// 找不到目標狀態，返回空列表return new List<Node>();
}

找到最終結點后，我們只需要從終點開始，一路沿著相鄰的OpenList結點中的最小值回溯即可找到尋路的路徑。

---

Unity中的A*算法

Unity中的A算法是一種常用的尋路算法，用于計算在網格或圖形地圖上找到最短路徑。A算法基于圖搜索和啟發式評估，具有較高的效率和準確性。

其實Unity中要使用A*算法，就是對地圖模型的抽象，將其抽象為結點構成的圖。我們可以分割網格，或者自定義結點坐標來實現。總之原理是一樣的，就是需要抽象出結點的概念：

1. 創建網格或圖形地圖：將游戲場景分割為一系列網格或節點，并構建地圖數據結構，用于存儲每個節點的信息，如位置、連接關系和代價。
2. 定義節點的啟發式評估函數：A*算法使用啟發式函數來估計從當前節點到目標節點的代價。這個函數通常基于節點之間的距離或其他因素，用于指導搜索過程。
3. 實現Open列表和Closed列表：Open列表存儲待評估的節點，Closed列表存儲已評估過的節點。開始時，將起始節點添加到Open列表中。
4. 迭代搜索過程：循環執行以下步驟直到找到目標節點或Open列表為空：
   1. 從Open列表中選擇代價最小的節點，作為當前節點。
   2. 將當前節點從Open列表中移除，并添加到Closed列表中。
   3. 檢查當前節點是否為目標節點，如果是，則路徑搜索完成。
   4. 否則，對當前節點的相鄰節點進行遍歷

A*算法的性能和效果受到地圖復雜度、啟發式函數的選擇以及路徑平滑等因素的影響。在實際使用中，可以根據具體需求對算法進行調優和優化

---

A*優化建議

如果需要對A*算法進行性能優化，可以考慮以下幾點：

1. 使用優先隊列：A*算法需要頻繁地從開放列表中取出具有最小代價的節點，因此使用優先隊列可以提高算法的效率。
2. 使用啟發式算法：啟發式算法可以在搜索過程中盡可能地快速地找到目標節點，從而提高算法效率。在實現過程中，需要設計一個好的估價函數，以便盡可能減少搜索的節點數。（好像煉丹啊）
3. 剪枝：A*算法中有一些無用的搜索節點，可以使用剪枝技術將其剪掉，從而減少搜索時間。
4. 預處理：預處理是指對搜索的地圖進行預處理，以便在搜索過程中可以快速地獲取地圖信息，從而提高搜索效率。

還有一種針對靜態地圖的優化方法：使用預處理的路線圖（Precomputed Roadmap）。

預處理的路線圖是一種離線生成的數據結構，它將地圖劃分為一些相互連接的區域，并計算出每個區域之間的最短路徑。在搜索過程中，可以直接使用預處理的路線圖，從而避免了大量的搜索操作。