一、滑動窗口概述

滑動窗口（Sliding Window）是一種用于解決數組（或字符串）中子數組（或子串）問題的有效算法。

Sliding Window核心思想：

滑動窗口技術的基本思想是維護一個窗口（一般是一個子數組或子串），該窗口在數組上滑動，并在滑動過程中更新窗口的內容。

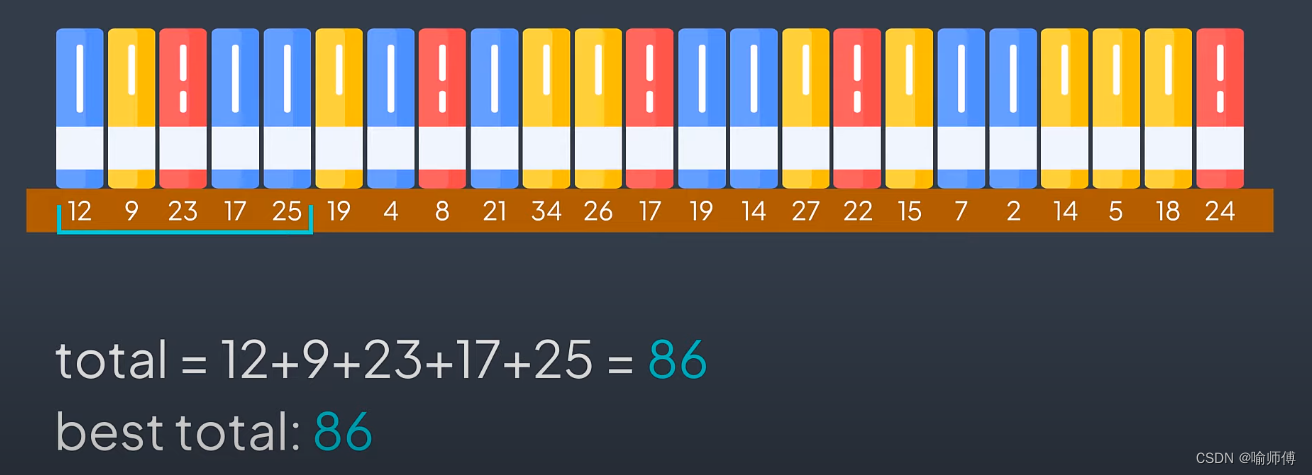
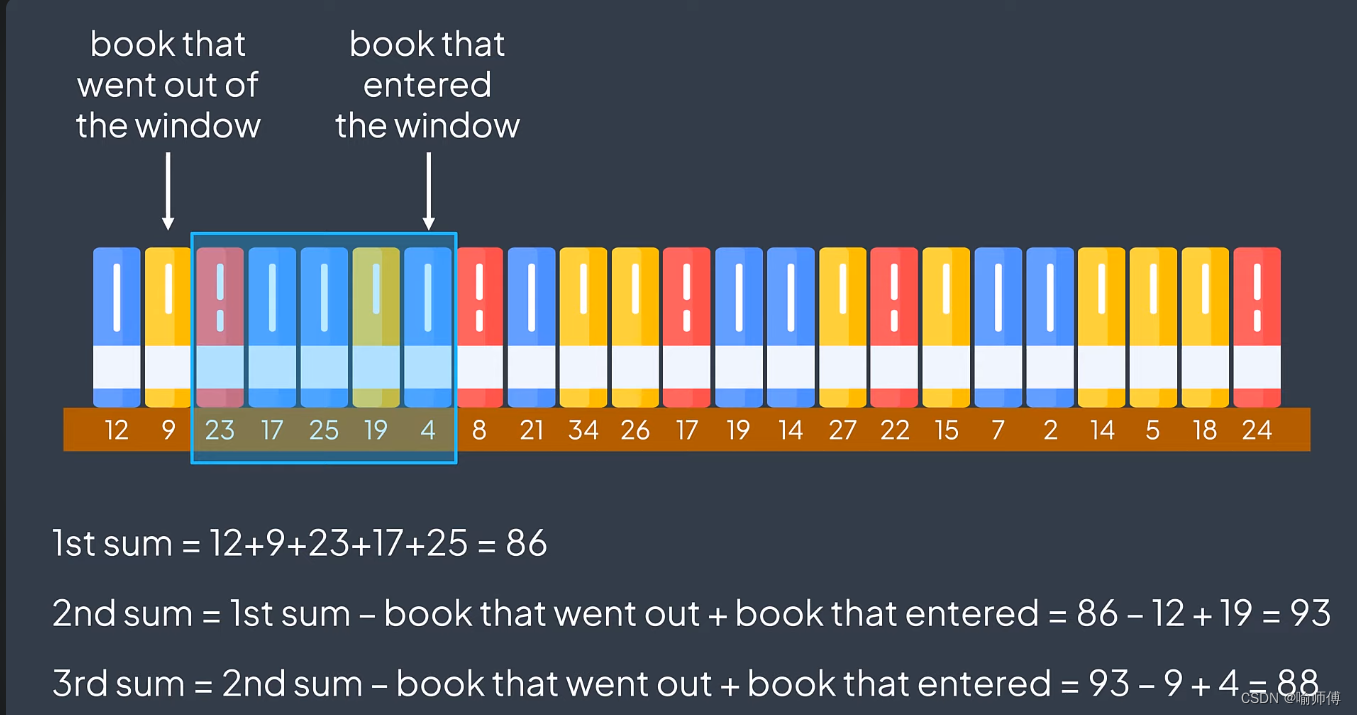
通過滑動窗口，可以在 ( O(n) ) 的時間復雜度內解決很多子數組（子串）問題，其中 ( n ) 是數組（字符串）的長度。

基本步驟：

1. 初始化窗口： 定義一個窗口的起始位置和結束位置，通常是兩個指針 left 和 right。
2. 滑動窗口： 不斷地增加 right 指針來擴大窗口，直到窗口滿足某個條件為止。

3. 更新窗口： 一旦滿足條件，嘗試縮小窗口大小，即增加 left 指針，直到條件不滿足為止。
4. 記錄結果： 在滑動窗口的過程中，根據題目要求來記錄最終的結果。

---

二、習題合集

LeetCode 209 長度最小的子數組

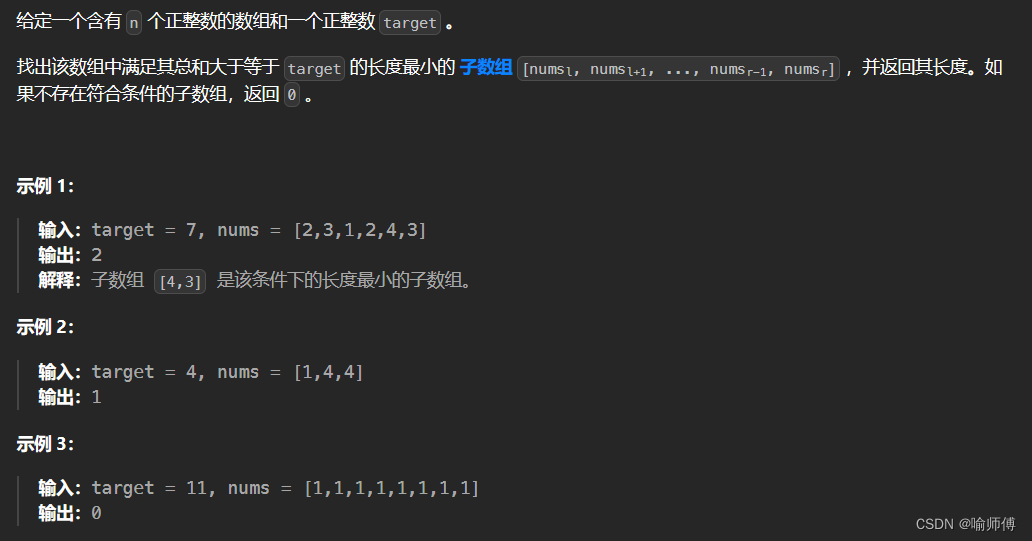
• 滑動窗口O（N）解法：

class Solution {public int minSubArrayLen(int target, int[] nums) {int n = nums.length;  // 數組的長度int ans = Integer.MAX_VALUE;  // 初始化結果為最大值，用于存儲最短子數組的長度int l = 0;  // 左指針，指向滑動窗口的起始位置int sum = 0;  // 記錄滑動窗口內元素的和for (int r = 0; r < n; r++) {  // 右指針，擴展滑動窗口sum += nums[r];  // 將右指針指向的元素加入窗口while (sum >= target) {  // 當窗口內元素和大于等于目標值時，嘗試縮小窗口ans = Math.min(ans, r - l + 1);  // 更新最短子數組的長度sum -= nums[l];  // 縮小窗口，左指針向右移動，減少窗口內的元素和l++;  // 左指針右移}}return ans == Integer.MAX_VALUE ? 0 : ans;  // 如果找不到滿足條件的子數組，返回0；否則返回最短子數組的長度}
}

---

LeetCode 3 無重復字符的最長子串

---

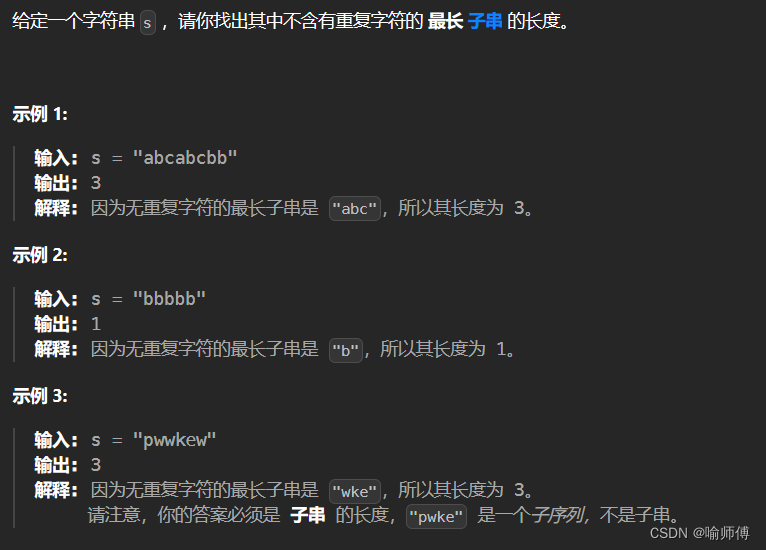
• 第一版滑動窗口

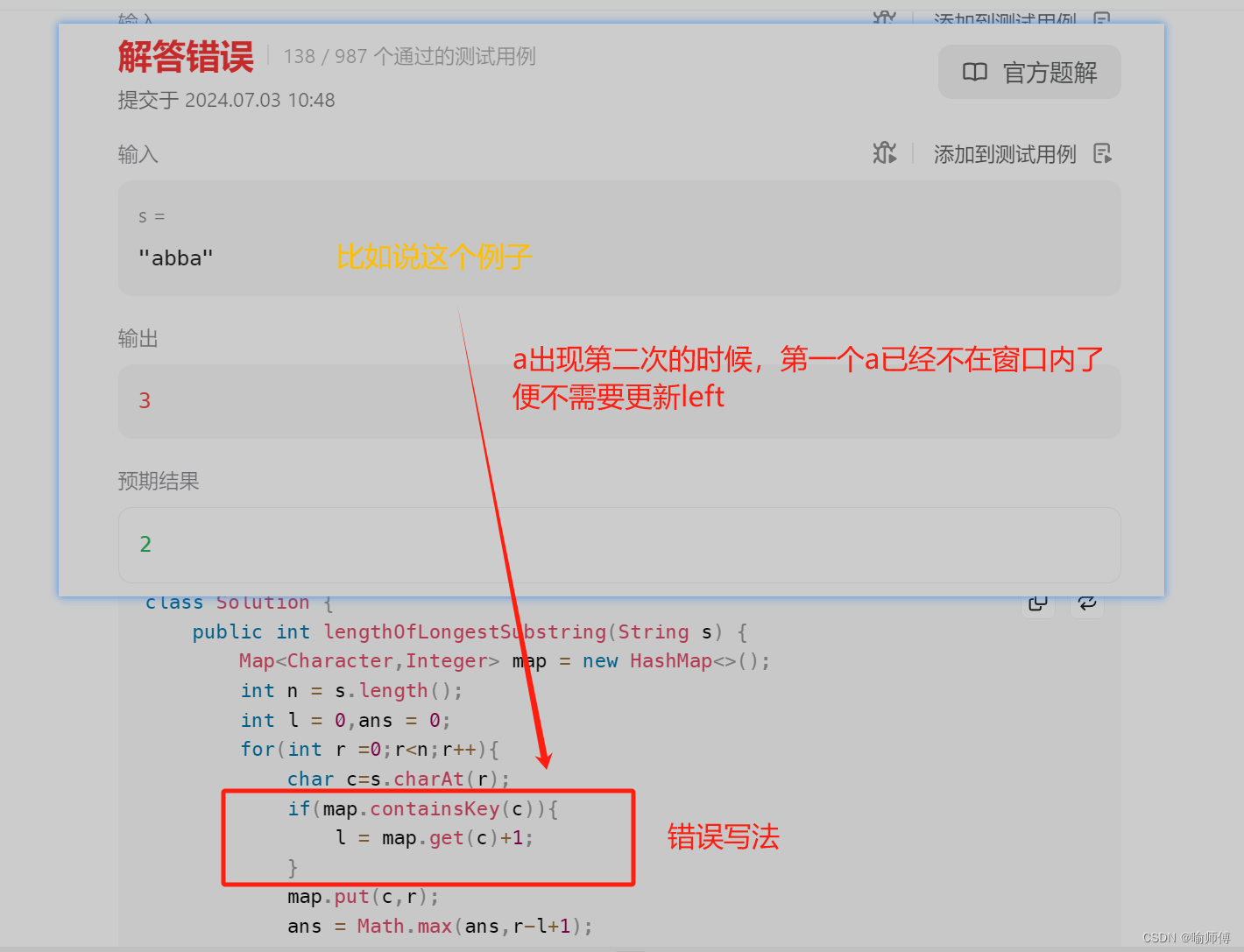
class Solution {public int lengthOfLongestSubstring(String s) {Map<Character, Integer> map = new HashMap<>(); // 創建一個哈希表，用來記錄字符及其出現的最后位置int n = s.length(); // 字符串的長度int l = 0, ans = 0; // l表示當前不重復子串的起始位置，ans用來記錄最長不重復子串的長度for (int r = 0; r < n; r++) {char c = s.charAt(r); // 獲取當前字符if (map.containsKey(c)) {//如果曾經出現的 字母 還在窗口內 —— l更新到 該位置+1//如果曾經出現的 字母 已不在當前窗口內了—— 則不需要更新l = Math.max(l,map.get(c)+1);}map.put(c, r); // 更新當前字符的最后出現位置為當前索引rans = Math.max(ans, r - l + 1); // 更新最長不重復子串的長度}return ans; // 返回最長不重復子串的長度}
}

要理解 left = Math.max(left,map.get(s.charAt(i)) + 1);需要回歸到滑動窗口的原理上。

窗口中始終是無重復字母的字符串。 我們通過窗口的左界和右界控制窗口。

右界不用特意操作，因為它是+1，+1地漲上去，記得在循環里+1就好。

左界：每當有一個字符曾經出現過，就需要判斷左界。

重點來了：

若，被判斷的字符上一次出現的位置就在滑動窗口內，即 [ i，j ] 內， 則需要left改變位置，改變為該字符上次出現位置+1。也就是left = map.get(s.charAt(i)) + 1的情況。

例如：

abcdb中，窗口正常運行到abcd時，下一個字符為b，b上一次出現在實在窗口里，所以需要把left設置為上一次出現的位置+1的位置，得到新的窗口為cdb，不然你不這樣設置，窗口里有重復的字符（bcdb），不符合窗口的定義。

若，不在滑動窗口內，則不用管。 不用管是因為：窗口中字符串沒有重復字符。窗口符合定義。所以left = left。 left = left就表示這個窗口暫時不變。

---

• 第二版優化的滑動窗口：

class Solution {public int lengthOfLongestSubstring(String s) {// 記錄字符上一次出現的位置int[] last = new int[128]; // 創建一個長度為128的整型數組，用來記錄ASCII碼表中每個字符上一次出現的位置for(int i = 0; i < 128; i++) {last[i] = -1; // 初始化數組，所有字符的上一次出現位置都設為-1，表示尚未出現過}int n = s.length(); // 字符串s的長度int res = 0; // 用于記錄最長的不重復子串的長度int start = 0; // 窗口開始位置，用來維護當前不重復子串的起始位置for(int i = 0; i < n; i++) {int index = s.charAt(i); // 獲取當前字符的ASCII碼作為索引start = Math.max(start, last[index] + 1); // 更新窗口的起始位置，確保不重復的起點res = Math.max(res, i - start + 1); // 更新最大的不重復子串長度last[index] = i; // 更新當前字符的最后出現位置為當前索引i}return res; // 返回最長的不重復子串的長度}
}

---

LeetCode 187 重復的DNA序列

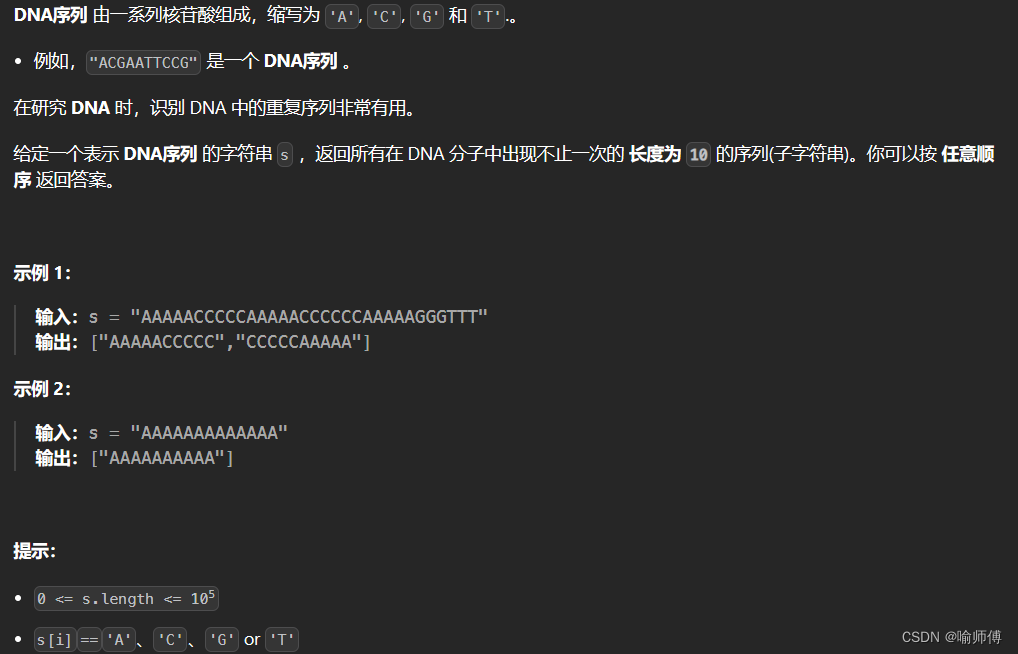
• 哈希表法~

class Solution {public List<String> findRepeatedDnaSequences(String s) {List<String> ans = new ArrayList<>(); // 用于存放重復的DNA序列int n = s.length(); if (n < 10) return ans; // 如果字符串長度小于10，直接返回空列表，因為無法形成長度為10的序列Map<String, Integer> map = new HashMap<>(); // 創建一個哈希表，用來記錄每個長度為10的子序列及其出現的次數map.put(s.substring(0, 10), 1); // 初始化，將第一個長度為10的子序列放入哈希表中for (int i = 1; i + 10 <= n; i++) { // 從第二個子序列開始遍歷到倒數第十個子序列String ss = s.substring(i, i + 10); // 獲取當前長度為10的子序列if (map.getOrDefault(ss, 0) == 1) { // 如果該子序列已經在哈希表中出現過一次ans.add(ss); // 將該子序列加入結果列表}map.put(ss, map.getOrDefault(ss, 0) + 1); // 更新哈希表中該子序列的出現次數}return ans; // 返回重復的DNA序列列表}
}

• 滑動窗口法~

class Solution {// 滑動窗口法查找重復的長度為10的DNA序列public List<String> findRepeatedDnaSequences(String s) {List<String> ans = new ArrayList<>(); // 用于存放重復的DNA序列int n = s.length(); // 字符串的長度if (n < 10) return ans; // 如果字符串長度小于10，直接返回空列表，因為無法形成長度為10的序列StringBuilder sb = new StringBuilder(s.substring(0, 10)); // 初始化第一個長度為10的子串Set<String> set = new HashSet<>(); // 使用集合來記錄出現過的子串set.add(sb.toString()); // 將第一個子串添加到集合中for (int i = 1; i + 10 <= n; i++) {String str = s.substring(i, i + 10); // 獲取當前長度為10的子串if (set.contains(str)) { // 如果集合中已經包含當前子串if (!ans.contains(str)) // 且列表中還未包含該子串ans.add(str); // 將該子串添加到列表中} else { // 如果集合中不包含當前子串set.add(str); // 將當前子串添加到集合中}}return ans; // 返回存放了重復DNA序列的列表}
}

---

LeetCode 424 替換后的最長重復字符

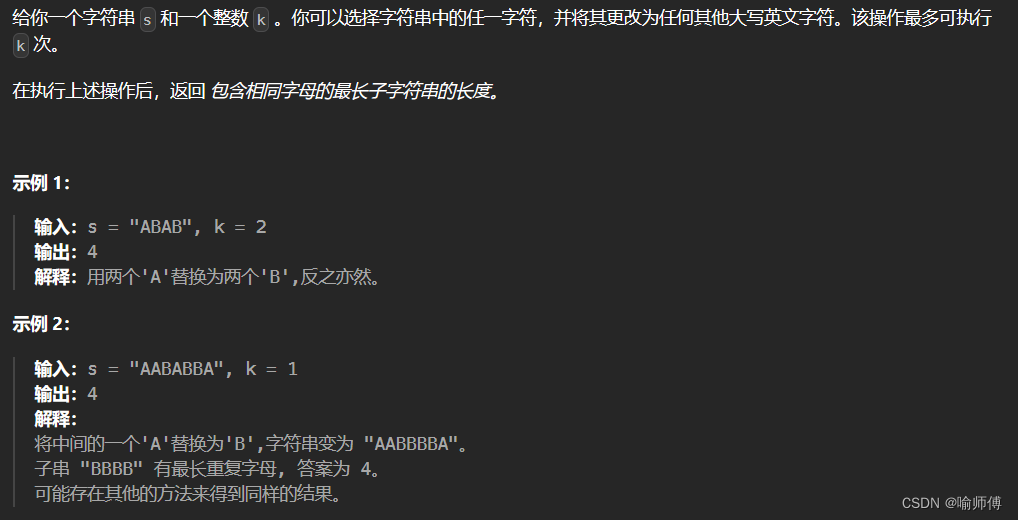
• 核心思想：

相同的最長子字符串(窗口) = 窗口內最大字符個數 + 反轉次數

一旦 窗口長度 - 窗口內最大字符個數 > 反轉次數 窗口開始移動

public int characterReplacement(String s, int k) {int n = s.length();if(n<2) return n;int ans = 0; // 用于存儲最長連續相同字符的子串的長度int maxFreq = 0; // 用于存儲當前窗口內出現次數最多的字符的次數char[] c = s.toCharArray();int[] freq = new int[26]; // 記錄當前窗口內每個字符出現的次數int left = 0; // 滑動窗口的左邊界for (int right = 0; right < n; right++) {++freq[c[right] - 'A']; // 更新右邊界字符的出現次數maxFreq = Math.max(maxFreq, freq[c[right] - 'A']); // 更新最大出現次數// 如果當前窗口的大小減去出現次數最多的字符的次數大于k，則需要縮小窗口// 使得窗口內可以通過替換字符使其變成連續相同字符的子串if (right - left + 1 > maxFreq + k) {freq[c[left] - 'A']--; // 縮小窗口時，更新左邊界字符的出現次數left++; // 縮小窗口}// 更新最長連續相同字符的子串的長度ans = Math.max(ans, right - left + 1);}return ans;}

---

---

更新于：