周賽

三角形的最大高度

給你兩個整數 red 和 blue，分別表示紅色球和藍色球的數量。你需要使用這些球來組成一個三角形，滿足第 1 行有 1 個球，第 2 行有 2 個球，第 3 行有 3 個球，依此類推。

每一行的球必須是 相同 顏色，且相鄰行的顏色必須 不同。

返回可以實現的三角形的 最大 高度。

示例 1：

輸入： red = 2, blue = 4

輸出： 3

解釋：

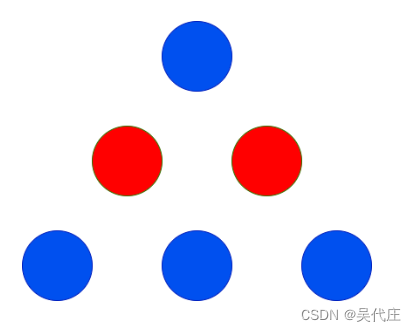
上圖顯示了唯一可能的排列方式。

解題思路

三角形的首行可能放置紅色球或藍色球，當首行顏色確定之后，三角形的每一行的顏色都可以確定。

對于兩種情況，分別枚舉每一行，計算是否可以使用指定顏色的球完整放置該行，可以使用指定顏色的球完整放置的最大行數即為三角形的最大高度。

class Solution {public int maxHeightOfTriangle(int red, int blue) {return Math.max(getMaxHeight(new int[]{red, blue}), getMaxHeight(new int[]{blue, red}));}public int getMaxHeight(int[] counts) {int height = 0;int position = 0;while (height + 1 <= counts[position]) {height++;counts[position] -= height;position ^= 1;}return height;}
}

找出有效子序列的最大長度 I

給你一個整數數組 nums。

nums 的子序列 sub 的長度為 x ，如果其滿足以下條件，則稱其為 有效子序列：

(sub[0] + sub[1]) % 2 == (sub[1] + sub[2]) % 2 == … == (sub[x - 2] + sub[x - 1]) % 2
返回 nums 的 最長的有效子序列 的長度。

一個 子序列 指的是從原數組中刪除一些元素（也可以不刪除任何元素），剩余元素保持原來順序組成的新數組。

示例 1：

輸入： nums = [1,2,3,4]

輸出： 4

解釋：

最長的有效子序列是 [1, 2, 3, 4]。

解題思路

對于子序列 sub，每對連續元素的和應具有相同的奇偶性

class Solution {public int maximumLength(int[] nums) {int c = nums[0] % 2, odd = 0, even = 0, both = 0;//both 記錄01，10交替出現的長度for (int num: nums){int cur = num % 2;if (cur==0){even++;}else{odd++;}if (cur == c){both++;c^=1;}}return Math.max(both, Math.max(even, odd));}
}

找出有效子序列的最大長度 II

給你一個整數數組 nums 和一個 正 整數 k 。
nums 的一個
子序列
sub 的長度為 x ，如果其滿足以下條件，則稱其為 有效子序列 ：

(sub[0] + sub[1]) % k == (sub[1] + sub[2]) % k == … == (sub[x - 2] + sub[x - 1]) % k
返回 nums 的 最長有效子序列 的長度。

示例 1：

輸入：nums = [1,2,3,4,5], k = 2

輸出：5

解釋：

最長有效子序列是 [1, 2, 3, 4, 5] 。

解題思路

通過一個兩層循環，預處理出能與nums[i]產生余數rem的右側第一個nums[j]，用哈希表記錄下標j。然后檢查n個起點所有可能的余數對應的最長的子序列長度，由于前述的預處理，我們可以快速地查出來下一個下標，查不出來說明子序列結束。

class Solution {public int maximumLength(int[] nums, int k) {int n = nums.length;Map<Integer, Integer>[] next = new Map[nums.length];Arrays.setAll(next, key -> new HashMap<>());for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {int rem = (nums[i] + nums[j]) % k;next[i].putIfAbsent(rem, j);}}int[][] memo = new int[n][k + 1];for (var it : memo) {Arrays.fill(it, -1);}int ans = 0;for (int i = 0; i < n; i++) {for (int r : next[i].keySet()) {ans = Math.max(ans, dfs(next, i, r, memo));}}return ans + 1;}private int dfs(Map<Integer, Integer>[] next, int i, int rem, int[][] memo) {if (memo[i][rem] != -1) {return memo[i][rem];}if (!next[i].containsKey(rem)) {return 0;}return memo[i][rem] = 1 + dfs(next, next[i].get(rem), rem, memo);}
}

合并兩棵樹后的最小直徑

給你兩棵 無向 樹，分別有 n 和 m 個節點，節點編號分別為 0 到 n - 1 和 0 到 m - 1 。給你兩個二維整數數組 edges1 和 edges2 ，長度分別為 n - 1 和 m - 1 ，其中 edges1[i] = [ai, bi] 表示在第一棵樹中節點 ai 和 bi 之間有一條邊，edges2[i] = [ui, vi] 表示在第二棵樹中節點 ui 和 vi 之間有一條邊。

你必須在第一棵樹和第二棵樹中分別選一個節點，并用一條邊連接它們。

請你返回添加邊后得到的樹中，最小直徑 為多少。

一棵樹的 直徑 指的是樹中任意兩個節點之間的最長路徑長度。

示例 1：

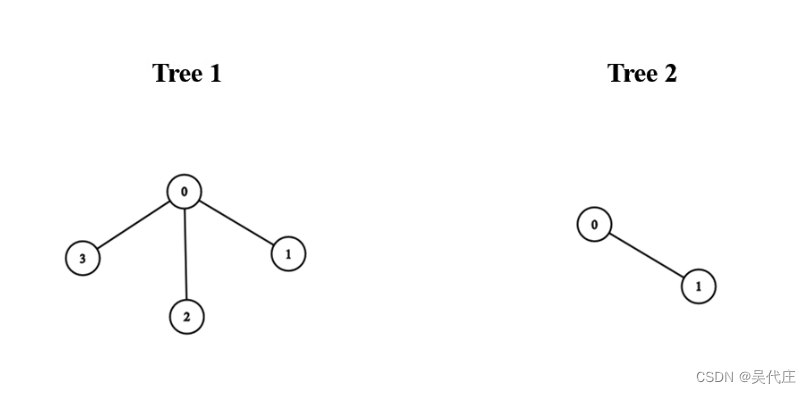
輸入：edges1 = [[0,1],[0,2],[0,3]], edges2 = [[0,1]]

輸出：3

解釋：

將第一棵樹中的節點 0 與第二棵樹中的任意節點連接，得到一棵直徑為 3 得樹。

class Solution {int diameter;public int minimumDiameterAfterMerge(int[][] edges1, int[][] edges2) {int diameter1 = treeDiameter(edges1), diameter2 = treeDiameter(edges2);int semiDiameter1 = (diameter1 + 1) / 2, semiDiameter2 = (diameter2 + 1) / 2;return Math.max(Math.max(diameter1, diameter2), semiDiameter1 + semiDiameter2 + 1);}public int treeDiameter(int[][] edges) {diameter = 0;int n = edges.length + 1;List<Integer>[] adjacentArr = new List[n];List<Integer>[] childrenArr = new List[n];for (int i = 0; i < n; i++) {adjacentArr[i] = new ArrayList<Integer>();childrenArr[i] = new ArrayList<Integer>();}for (int[] edge : edges) {adjacentArr[edge[0]].add(edge[1]);adjacentArr[edge[1]].add(edge[0]);}getTree(adjacentArr, childrenArr, -1, 0);getDepth(childrenArr, 0);return diameter;}public void getTree(List<Integer>[] adjacentArr, List<Integer>[] childrenArr, int parent, int curr) {if (parent >= 0) {childrenArr[parent].add(curr);}List<Integer> adjacent = adjacentArr[curr];for (int next : adjacent) {if (next != parent) {getTree(adjacentArr, childrenArr, curr, next);}}}public int getDepth(List<Integer>[] childrenArr, int node) {List<Integer> children = childrenArr[node];int first = 0, second = 0;for (int child : children) {int depth = getDepth(childrenArr, child);if (depth > first) {second = first;first = depth;} else if (depth > second) {second = depth;}diameter = Math.max(diameter, first + second);}return first + 1;}
}

解題思路

這道題給定兩個無向樹，要求在兩個樹中各選擇一個結點，使用一條邊連接這兩個結點得到合并后的樹，計算合并后的樹的最小直徑。

來源

LeetCode