模擬退火算法來源于固體退火原理，將固體加溫至充分高，再讓其徐徐冷卻，加溫時，固體內部粒子隨溫升變為無序狀，內能增大，而徐徐冷卻時粒子漸趨有序，在每個溫度都達到平衡態，最后在常溫時達到基態，內能減為最小。

SA在某一初溫下，伴隨溫度參數的不斷下降，結合概率突跳特性在解空間中隨機尋找目標函數的全局最優解。

模擬退火算法是利用問題的求解過程與熔化物體退火過程的相似性,采用隨機模擬物體退火過程來完成問題的求解，也就是在控制參數(溫度)的作用下對參數的值進行調整,直到所選取的參數值最終使能量函數達到全局極小值。

模擬退火算法目的

1. 許多實際優化問題的目標函數都是非凸的, 存在許多局部最優解, 但是, 有效地求出一般非凸目標函數的全局最優解至今仍是一個難題。特別是隨著優化問題規模的增大, 局部最優解的數目將會迅速增加.
2. 模擬退火算法是利用問題的求解過程與熔化物體退火過程的相似性,采用隨機模擬物體退火過程來完成問題的求解，也就是在控制參數(溫度)的作用下對參數的值進行調整,直到所選取的參數值最終使能量函數達到全局極小值。

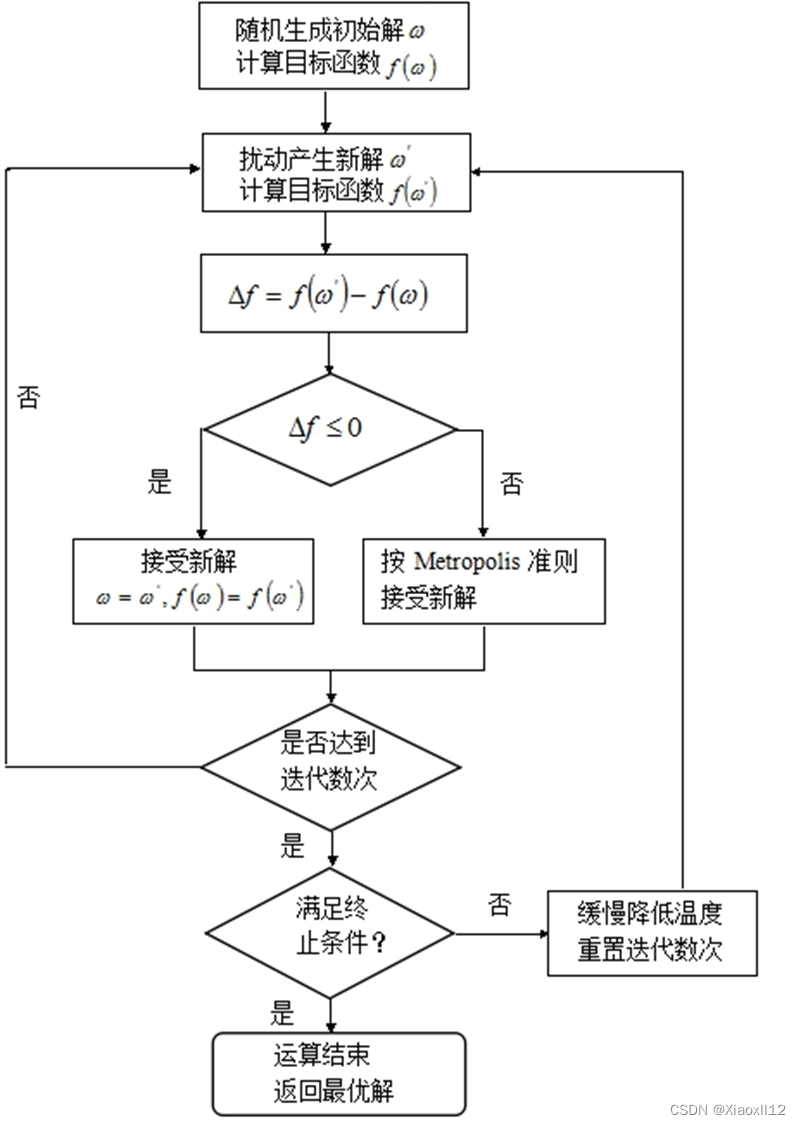
模擬退火算法流程

1. 初始化：針對問題選定合適的目標函數f作為能量函數E；決定初始參數:起始溫度T 、終止溫度、冷卻率α(α∈[0,1])、單一溫度迭代次數k。
2. 設定起始迭代次數t=0，產生初始狀態X0，計算其能量E0。
3. 以目前解為中心由狀態產生函數產生新的鄰近解X1，計算其能量E1。
4. 采用Metropolis接受法則比較兩狀態的能量，判決是否接受X1 , 若接受, 則令當前狀態等于X1 , 若不接受,則令當前狀態等于X0；
5. 更新迭代次數，判斷是否達到設定的閾值k，若是則進行降溫T=T*α，且令t=0。
6. 判斷溫度是否達到終止溫度，若是則順序執行step 7;若否則轉至step 3重復執行

當前解作為最優解輸出。