引言

聚類是一種強大的機器學習方法，用于根據特征空間中元素的接近程度發現相似的模式。它廣泛用于計算機科學、生物科學、地球科學和經濟學。盡管已經開發了最先進的基于分區和基于連接的聚類方法，但數據中的弱連接性和異構密度阻礙了其有效性。在這項工作中，我們提出了一種使用局部方向中心性（CDC）的邊界搜索聚類算法。它采用基于 K 最近鄰 （KNN） 分布的密度無關度量來區分內部點和邊界點。邊界點生成封閉的籠子來綁定內部點的連接，從而防止跨聚類連接并分離弱連接的聚類。我們通過在具有挑戰性的合成數據集中檢測復雜的結構簇，從單細胞RNA測序（scRNA-seq）和質譜細胞術（CyTOF）數據中識別細胞類型，識別語音語料庫上的說話者，并在各種類型的真實世界基準上作證，來證明CDC的有效性。

T_DCM（或ratio）是通過二維空間中三角不規則網絡 （TIN） 的圖論分析來估計的。通常，邊界點往往比內部點具有較低的中心性（即較高的 DCM）。因此，我們按降序對所有 DCM 進行排序，如果給定邊界點數，則可以搜索最佳 T_DCM（或ratio）。

聚類算法的過程

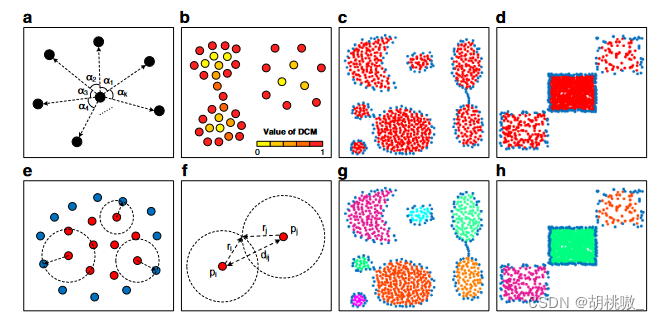
CDC的核心思想是根據KNN的分布來區分集群的邊界點和內部點。邊界點勾勒出簇的形狀，并生成籠子以綁定內部點的連接。簇的內部點趨向于在各個方向上都被相鄰點包圍，而邊界點僅包括一定方向范圍內的相鄰點。為了測量方向分布的這種差異，我們將 KNN 在 2D 空間中形成的角度方差定義為局部方向中心度量 （DCM）：
$$DCM=\frac{1}{k}\sum _{i=1}^k({\alpha }_i?\frac{2\pi }{k}{)}^2$$
中心點的 KNNs 可以形成 k 個角 α1、α2…αk（圖a）。對于二維角，條件 ${\sum }_{i=1}^k{\alpha }_i=2\pi$成立。當且僅當所有角度相等時，DCM 達到最小值 0。這種情況意味著中心點的 KNN 在所有方向上均勻分布。當其中一個角度為 2π 而其余角度為 0 時，它可以最大化為$\frac{4(k?1)n^2}{k^2}$。當 KNN 沿同一方向分布時，就會發生這種極端情況。根據極值，DCM 可以歸一化為 [0， 1] 范圍，如下所示：
$$DCM=\frac{k}{4(k?1)n^2}\sum _{i=1}^k({\alpha }_i?\frac{2\pi }{k}{)}^2$$

DCM計算結果表明，團簇內部點的DCM值相對較低，邊界點的DCM值較高（圖b）。因此，內部點和邊界點可以用閾值T_DCM劃分。DS5 和 DS7 兩個合成數據集的劃分結果驗證了其有效性（圖c、d）。為了保證內部點 p1， p2， …，p_m 在周圍邊界點 q1， q2， …， q_n?m 限制的區域內相互連接，我們將內部點 pi 與所有邊界點之間的最小距離定義為其可到達距離：
$$r_i=mi{n}_{j=1}^{n?m}d(p_i,q_j)$$
其中 d（pi，qj） 是兩點 pi 和 qj 之間的距離（圖 e）。如果保證以下關聯規則，則兩個內部點可以連接為同一簇：
$$d(p_i,p_j)\le r_i+r_j$$
其中 ri 和 rj 分別是內部點 pi 和 pj 的可達距離（圖f）。在正確識別邊界點的前提下（邊界點識別不完全的極端情況除外），內部點的連接被限制在邊界點定義的區域內。如果兩個內部點之間存在跨聚類連接，則邊界點將包含在由其可到達距離定義的范圍內，這與可到達距離的定義相沖突。因此，同一聚類的內部點可以被困在由邊界點組成的同一外部輪廓中，并且基于此關聯規則將避免跨聚類連接。DS5 和 DS7 的連接結果是通過將規則應用于除法結果而生成的（圖 g、h）。雖然DS5和DS7中的簇對連接較弱，DS7中的三個簇的密度差異很大，但所有簇都被準確識別。

在計算 DCM 并連接內部點后，我們通過將每個邊界點分配給其最近的內部點所屬的集群來完成該過程。CDC 包含兩個可控參數，k 和 T_DCM。k 調整最近鄰的數量，T_DCM 確定內部點和邊界點的劃分。CDC的偽代碼詳見附注2。在實踐中，考慮到 T_DCM 隨數據分布而變化，我們采用內部點的百分位數比率ratio來確定 T_DCM 作為按降序排序的[n?（1–ratio）]的 DCM。參數ratio具有直觀的物理含義和更好的穩定性，這使得它比T_DCM更容易指定。根據我們的實驗，70%~99%的內點是建議的默認參數比率范圍，以獲得有希望的聚類結果。然而，當聚類相互混合時，需要更多的邊界點（較低的比率）來分離閉合的聚類。

k的經驗估計方法

通過對參數敏感度的分析和已有的研究，我們知道k是一個不敏感的參數，與數據集中的點數n有關。因此，我們提出了一種經驗方法，將 k 和 n 之間的關系形式化為：
$$k=\{\begin{array}{ll}?\frac{\pi }{50}???\frac{\pi }{20}?& \text{if?}100\le n\le 1000\\ ?lo{g}_2(n)+10??5?lo{g}_2(n)?& \text{if?}n\ge 1000\end{array}$$
$??$表示向上取整。

估計用于確定T_DCM的邊界點數：

構建了一個三角不規則網絡（TIN）(圖a)來連接所有點。在圖論中，頂點的度數定義為入射到頂點的邊數，每條邊連接兩個頂點。基于這一定律
$$\sum _{i=1}^{V}deg(v_i)=2E$$
deg（v_i） 表示頂點 v_i 的度數，V 表示頂點總數，E 表示邊的總數。

對于具有單個連接分量的 TIN，邊界點的總數等于最外邊的總數。
$$\sum _{i=1}^{V}deg(v_i)=3F+B$$
F 和 B 分別表示三角形和邊界點的總數。

二維歐拉公式:
$$V+F?E=1$$
通過結合這些公式，我們可以推斷出 B 的解如下：
$$B=2V?F?2$$

但是，整個 TIN 中的初始邊界點數不等于分離聚類中的邊界點總數。為了進行準確的估計，應將整個 TIN 視為多個子網（圖 b）。給定 C 簇，簇中的邊界點數可以求解如下：
$$\sum _{i=1}^m{B}_i=2\sum _{i=1}^m{V}_i?\sum _{i=1}^m{F}_i?2C$$
$$B=2V?F?2C$$
其中 F 是多個分離網絡中簇內三角形的總數。V 在給定數據集（即 n）中是已知的，但 F 和 C 不是。初始F是整個TIN中三角形的總數，其中包括連接不同聚類的三角形，即三個頂點不都在同一聚類中的跨聚類三角形（否則為聚類內三角形）。使用過多的三角形會使邊界點 B 的數量小于真實值。為了識別跨聚類三角形，我們設置了一個判斷規則：
$$\sum _{i=1}^3\sum _{j=1,j\ne i}^3\sigma (v_i,v_j)<3$$
其中 v1、v2、v3 是三角形的三個頂點，σ（vi， vj）isan 指標函數：
$$\sigma (v_i,v_j)=\{\begin{array}{ll}0,& \text{if?}{v}_j\notin \text{KNN}(v_i)\\ 1,& \text{if?}{v}_j\in \text{KNN}(v_i)\end{array}$$
考慮聚類內三角形中頂點的鄰近性。最終的F可以計算為初始F減去滿足方程（16）的跨聚類三角形的數量（圖c）。就簇C的數量而言，通常遠小于V和F，這對B的估計有微不足道的影響，此外，CDC對DCM閾值的魯棒性如討論所述。因此，當 C 模糊或難以確定時，可以將其視為 1。

Code availability
The code of CDC in MATLAB, R and Python, and the toolkit with six applications can be downloaded at https://github.com/ZPGuiGroupWhu/ClusteringDirectionCentrality and https://zenodo.org/record/7029720#.YwuFsuxByZw. Digital Object Identifier https:// doi.org/10.5281/zenodo.7029720.