
一道經典遞歸題,兩種做法,常規遞歸做法和模擬數學規律解法
3695. 擴充序列 - AcWing題庫
擴充序列
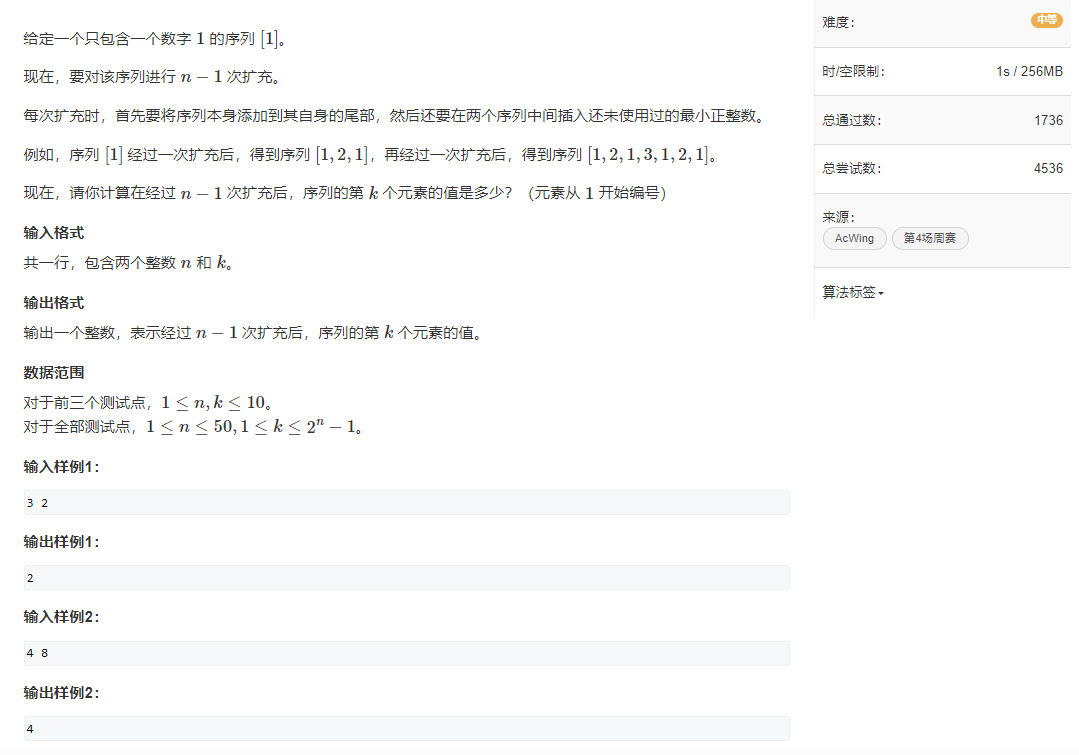
樣例解釋
對于樣例 1,經過 2 次擴充,得到序列 [1,2,1,3,1,2,1]其第 2 個元素為 2。
對于樣例 2,經過 3次擴充,得到序列 [1,2,1,3,1,2,1,4,1,2,1,3,1,2,1]其第 8個元素為 4。
思路一
先看序列的長度。N=1時,序列長度為1,N=2時,序列長度為3
N=3時,序列長度為7,N=4時,序列長度為15
不難看出規律
假設長度為Len,則N和長度的關系為
Len=pow(2,n)-1;則我們在算K時,有三種情況
情況1
是k=pow(2,n-1),則K是最中間那個數,也就是擴容第N-1次時,新增的那個數,通過樣例可以看出,新增的數,就是N本身,例如擴容3次,新增的數是4
1,2 ,1,3, 1,2, 1,4, 1,2, 1,3 ,1,2 ,1
所以直接返回N,即是結果,k的值
情況2
是k<pow(2,n-1),接著計算n=n-1時,k的值是多少
情況3
是k>pow(2,n-1),只需要把k-(pow(2,n-1)),然后按情況2計算即可,因為中點左右兩邊的序列,是一樣的
通過這三種情況,發現可以直接遞歸做,看一下數據范圍
n<50,最多是O(4n),時間復雜度沒問題,但是pow(2,50)爆int,需要longlong
實現代碼1
#include<iostream>
#include<cmath>
using namespace std;
typedef long long ll ;
ll n,k,res;
ll dfs(ll k){if(k==pow(2,n-1))return n;//情況一,確定是新增數,直接返回//如果是情況三,則變成情況二if(k>pow(2,n-1))k-=pow(2,n-1);//縮小范圍,只需要查找在上次擴充之前出現的數n-=1;//遞歸dfs(k);
}
int main(){cin>>n>>k;res=dfs(k);cout<<res;return 0;
}思路二
發現數列規律
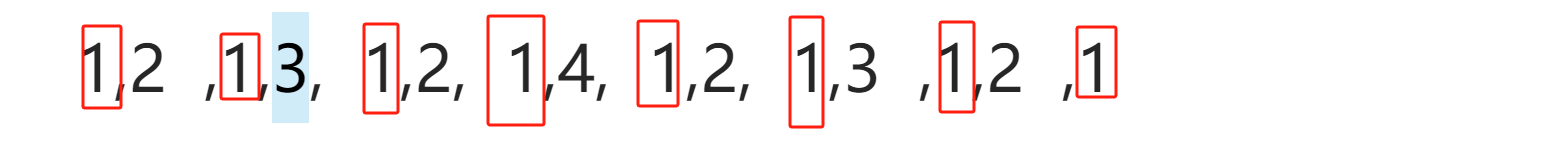
所有奇數位都是1,也就是如果k%2!=0,則k的值為1,這里我們只看值,則k是最初始的數
反之
如果k%2==0,則k一定是擴充的數,那么我們利用k,就可以推斷出,k位對應的值,是在第幾次擴充出現的
例如
1,2 ,1,3, 1,2, 1,4, 1,2, 1,3 ,1,2 ,1
紅4是第八位,對應的k是8,k/2=4,4/2=2,2/2=1,k能除以3次,所以k對應的值,是第三次擴充后出現
1,2 ,1,3, 1,2, 1,4, 1,2, 1,3 ,1,2 ,1
紅2是第十位,k=10,10/2=5,5是奇數,所以不用除了,k除了一次,k對應的值,是在第一次擴充時出現的
1,2 ,1,3, 1,2, 1,4, 1,2, 1,3 ,1,2 ,1
紅3是第十二位,k=12,12/2=6,6/2=3,3是奇數,不用除了,k除了一次,k對應的值,是在第二次擴充時出現的
第三次擴充出現的值是4,第二次擴充出現的值是3,第一次擴充出現的值是2
所以我們只需要計算,k對應的值是第幾次擴充時出現的,然后+1即可
實現代碼二
#include<iostream>
using namespace std;
typedef long long ll ;ll n,k,res=0;
int main(){cin>>n>>k;//k&1是位運算,如果&1為真,則k%2!=0while(!(k&1))k>>=1,res++;cout<<res+1;return 0;
}




)












)
