引言

• 頭一次產生了那么強烈的動搖，對于未來沒有任何的感覺的，不知道將會往哪里走，不知道怎么辦。可能還是因為實習吧，再加上最近復習也沒有什么進展，并不知道該怎么辦，投的提前批基本上沒什么回應，投的實習基本上都掛了。
• 在加上不在學校，沒有辦法和同學一塊共享信息，一個人總是覺得有點孤零零的，難受，并且是憂郁的。
• 想那么多也沒用，還是得繼續復習。按照我的計劃來。
• 上午出去有事，基本上沒有刷算法，下午才開始刷算法。

復習

數位DP——度的數量

• 這一類題型之前基本上都沒有做過，現在得好好補充一下，感覺聽名字和狀態壓縮DP很像。

注意

• X和Y是區間長度，是INT類型的數字的上限，并且只能是正數
• 左右區間的都是閉合的，所以臨界條件是兩邊相等，僅僅只有一個數字。

個人實現

• 首先，這里得先解決一個數字，才能解決所有的數字，所以得先專注于解決一個數字的判定。
• 這里是B的整數次冪，所以可以想成若干進制去思考，之前應該做過類似的出發是一個思路，肯定是能夠先用高次冪的結果進行表示，然后再用低次冪的結果進行表示。然后在判定這個數字能否用一個較低位進行表示，這道題就算是結束了。

#include <iostream>
#include <vector>using namespace std;int x,y,k,b;
vector<int> exp;int main(){cin>>x>>y;cin>>k>>b;// 保存b的不同次冪的中間結果int res = 0;int i=1;exp.push_back(1);for ( i = b; i <= y ; i *= b)exp.push_back(i);for (int i = x; i <= y; ++i) {// 判斷每一個數字是否能夠使用對應的數字進行保存int cnt = k,temp = i;for (int j = exp.size() - 1; j >= 0 ; j --) {if (exp[j] <= temp){temp -= exp[j];cnt --;if (cnt >= 0 ){if (cnt == 0 && temp == 0)res ++;}elsebreak;}}}cout<<res;
}

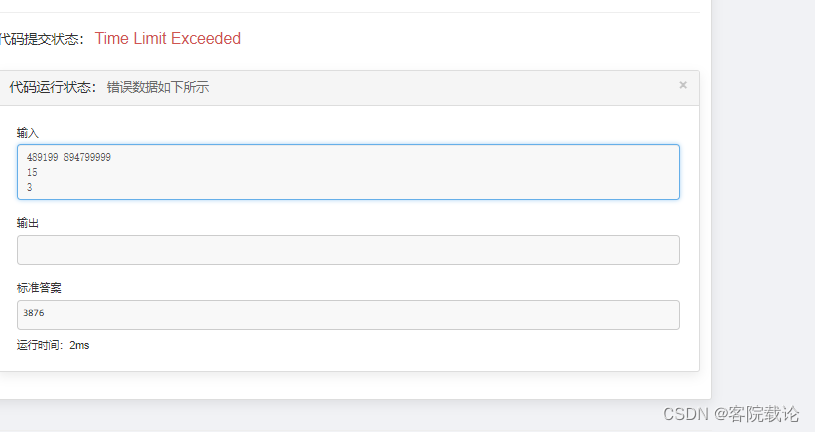
實驗結果如下

• 我的時間復雜度太高了，遍歷所有的數字，然后在遍歷每一個數字，看看能否出現對應的結果。相當于使（y - x） * k相當遠的平方的運算時間復雜度。
  

參考實現

• 這里應該是使用了數位DP，之前并沒有學過。

數位DP的相關技巧

• 區間轉成邊界相減問題：
  • 計算的區間【X，Y】中所有符合條件的數字，使用1到Y的所有符合條件的數字的數量，減去1到X中所有符合條件的數字的數量。【X，Y】 = f(Y) - f(X - 1)
• 從樹的角度去考慮數位DP問題
  • 對于每一個數字的位數，只有兩種情況，就是加入對應的分支以及不加入對應的分支等。

這里完全跳過了，看不懂，大約花了差不多一個小時，視頻講解有問題在加上題目的難度比較大，以后調整自己的復習思路，不在學習這種難度較高的算法題，主要還是刷對應的筆試題庫

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 35;int l, r, k, b;
int a[N], al;
int f[N][N];int dp(int pos, int st, int op) //op: 1=,0<
{//枚舉到最后一位數位，是否恰有k個不同的1（也是遞歸的終止條件）if (!pos) return st == k;//記憶化搜索，前提是不貼著上界（可以枚舉滿這一位所有的數字）if (!op && ~f[pos][st]) return f[pos][st];//01數位dp，貼著上界時，本輪能枚舉的最大數就是上界數位的數字和1之間的最小值int res = 0, maxx = op ? min(a[pos], 1) : 1;for (int i = 0; i <= maxx; i ++ ){if (st + i > k) continue;res += dp(pos - 1, st + i, op && i == a[pos]);}return op ? res : f[pos][st] = res;
}
int calc(int x)
{al = 0; memset(f, -1, sizeof f);        //模板的必要初始化步驟while (x) a[ ++ al] = x % b, x /= b;  //把x按照進制分解到數組中return dp(al, 0, 1);
}
int main()
{cin >> l >> r >> k >> b;cout << calc(r) - calc(l - 1) << endl;return 0;
}

作者：一只野生彩色鉛筆
鏈接：https://www.acwing.com/solution/content/66855/
來源：AcWing
著作權歸作者所有。商業轉載請聯系作者獲得授權，非商業轉載請注明出處。

總結

• 明天朋友來家里做客，忙完這一陣之后，就閉門謝客，專心好好準備秋招。馬上第一批就開始了，但是我的項目還是沒有準備好，進度太慢了，不行的。

• 我就在想，我真的有必要刷這么多算法進階題目嗎？今天的數位DP好難呀，感覺要花一上午，不如多花點時間去做熱搜題目的一百道題。感覺到此為止了，不想再花時間去做這寫題目了，數位DP太難了，根本就不會做。講的有問題。

• 不想浪費時間了，單純的針對一百熱題吧，不在刷什么難題了，只能用題庫堆起來，然后如果有不會的題目，再去看他的講解，不能在這樣往下跟了，然后每天上午的題目，就是單純復習現在已經學到的相關算法了。 我是找工作的，不是面對算法競賽的。

• 大概看了一下，就課程安排來說，雖然刷的是leetcode，但是還是會提到對應的題型進行講解，所以轉變以下自己的思路，不然這樣化的時間實在太多了，完全沒有必要。

• 而且我大概看了一下，基本上我在面試中遇到的問題，在這里基本上都能遇見，在騰訊面試中遇見的使用LRU，然后華為面試中遇見的三數之和等等。還是調整一下重點，重點圍繞以下兩個課題，分別是

  • leetcode熱題100道
  • 面試經典150道

• 差不多一天三到四道題，差不多一個月刷一遍，還能回顧一遍。不要浪費時間。