深度學習筆記: 最詳盡解釋邏輯回歸 Logistic Regression

歡迎收藏Star我的Machine Learning Blog:https://github.com/purepisces/Wenqing-Machine_Learning_Blog。如果收藏star, 有問題可以隨時與我交流, 謝謝大家！

邏輯回歸概述

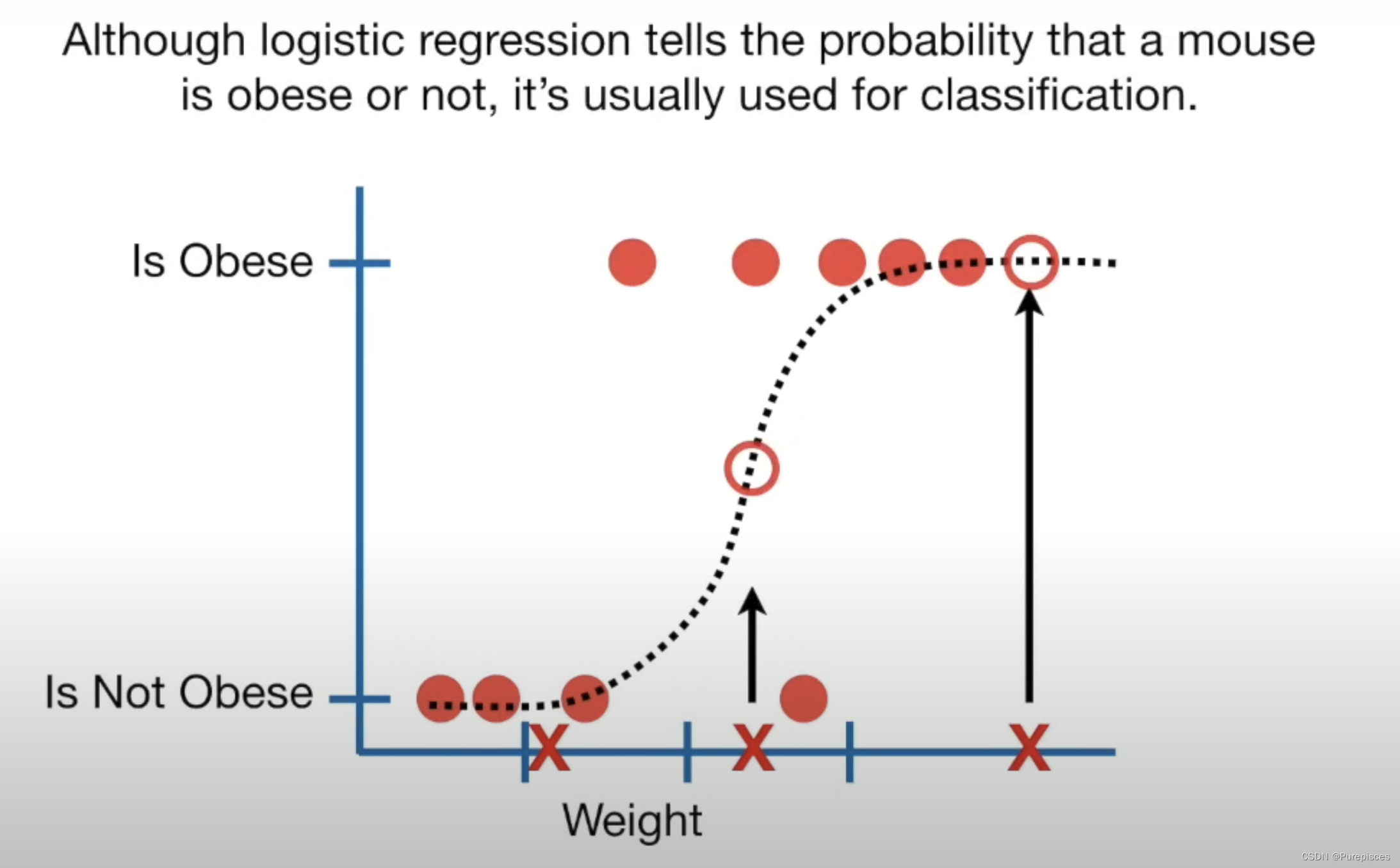
邏輯回歸類似于線性回歸，但預測的是某事物是否為真，而不是像大小這樣的連續值。邏輯回歸擬合的是“S”形的“邏輯函數”曲線，而不是一條直線。這個曲線從0到1，表示根據預測變量（例如體重），某個結果發生的概率（例如老鼠是否肥胖）。

邏輯回歸的工作原理

重的老鼠：高概率肥胖。
中等體重的老鼠：50%概率肥胖。
輕的老鼠：低概率肥胖。

雖然邏輯回歸給出了老鼠是否肥胖的概率，但它通常用于分類。例如，如果老鼠肥胖的概率大于50%，我們就將其分類為肥胖，否則分類為“不肥胖”。

alt

邏輯回歸中的預測變量

邏輯回歸可以處理連續數據（如體重、年齡）和離散數據（如基因型、星座）。我們可以測試每個變量是否對預測肥胖有用。與普通回歸不同，我們不能輕易地比較復雜模型和簡單模型。相反，我們測試一個變量對預測的影響是否顯著不同于0。如果不是，這意味著該變量對預測沒有幫助。我們使用沃爾德檢驗來確定這一點。

例如，如果肥胖是由體重+基因型+年齡+星座預測的，而我們發現星座“完全無用”（統計術語表示“沒有幫助”），我們可以從模型中排除它，以節省時間和資源。

邏輯回歸能夠提供概率并使用連續和離散測量值對新樣本進行分類，使其成為一種流行的機器學習方法。

線性回歸與邏輯回歸的區別

線性回歸和邏輯回歸的一個主要區別是數據擬合的方法：

線性回歸：使用“最小二乘法”擬合，最小化殘差的平方和。該方法允許計算R2來比較模型。
邏輯回歸：使用“最大似然法”。它沒有殘差，因此不能使用最小二乘法或計算R2。

在邏輯回歸中，您：

選擇一個概率，根據體重縮放，觀察肥胖老鼠的概率。
使用此概率計算觀察到的該體重的非肥胖老鼠的可能性。
然后計算觀察到該老鼠的可能性。
對所有老鼠重復此過程并將所有這些可能性相乘。這是給定該曲線的數據的可能性。

然后，您：

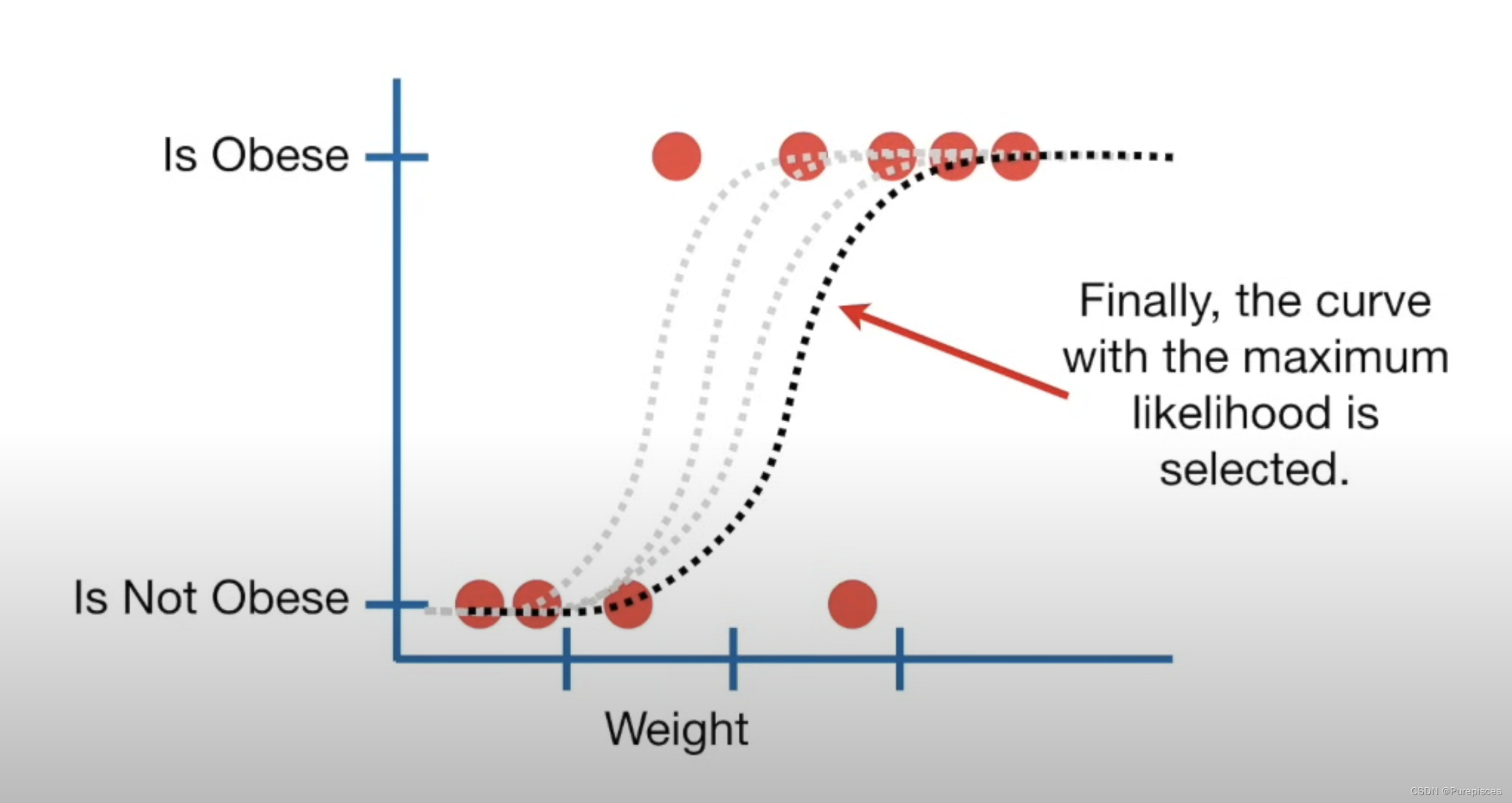
移動曲線。
計算新曲線的數據可能性。
重復此過程，直到找到最大可能性的曲線。

總結

邏輯回歸可以用于分類樣本，并且可以使用不同類型的數據（例如體重、基因型）進行分類。它還幫助評估哪些變量對分類有用（例如在使用體重、基因型、年齡和星座預測肥胖時，星座可能“完全無用”）。

關鍵概念

邏輯函數

邏輯回歸的核心是邏輯函數（也稱為S型函數），它將任何實值數映射到[0, 1]范圍內：

$\sigma(z) = \frac{1}{1 + e^{-z}}$

這里， $z$ 是輸入特征的線性組合。對于二分類，邏輯函數輸出給定輸入點屬于正類的概率。

決策邊界

決策邊界是我們分類輸出的閾值。對于二分類，一個常見的閾值是0.5：

如果輸出概率 $\geq 0.5$ ，則分類為類別1。
如果輸出概率 $< 0.5$ ，則分類為類別0。

模型表示

假設

在邏輯回歸中，假設定義為：

$h_\theta(x) = \sigma(\theta^T x)$

其中， $\theta$ 是權重向量， $x$ 是輸入特征向量， $\sigma$ 是S型函數。

代價函數

邏輯回歸的代價函數是對數損失（也稱為二元交叉熵）：

$J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right]$

其中， $m$ 是訓練樣本的數量， $y$ 是實際標簽， $h_\theta(x)$ 是預測概率。

優化

目標是找到使代價函數 $J(\theta)$ 最小化的參數 $\theta$ 。這通常使用梯度下降等優化算法來完成。

稀疏特征

在許多現實世界的應用中，特征空間是稀疏的，意味著大多數特征值為零。邏輯回歸在這些場景中特別有效，因為：

它可以高效地處理高維數據。
模型復雜度與特征數量線性相關，使其在計算上可行。

使用稀疏數據進行邏輯回歸時，我們通常使用稀疏矩陣表示（如壓縮稀疏行（CSR）或壓縮稀疏列（CSC）格式）來存儲輸入特征。
這些數據結構僅存儲非零元素及其索引，與密集矩陣相比顯著減少了內存使用。
邏輯回歸涉及矩陣乘法和其他線性代數操作。當數據存儲在稀疏矩陣中時，這些操作可以優化以忽略零元素，從而加快計算速度。

當使用正則化技術時，特別是L1正則化（也稱為套索正則化），邏輯回歸被認為是稀疏線性分類器。這種正則化技術可以迫使模型的一些系數正好為零，有效地忽略某些特征，從而導致稀疏模型。

該模型是線性的，因為它將對數幾率建模為輸入特征的線性組合。
$\log \left( \frac{p}{1-p} \right) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_n x_n$

在邏輯回歸的上下文中，“計算上可行”意味著：
訓練和預測的時間和內存需求隨著數據規模（特征和樣本數量）線性增長。

分布式訓練

為什么要分布式訓練？

隨著數據量的增加，在單臺機器上訓練模型會變得緩慢且不切實際。分布式訓練允許并行處理，使得能夠高效地處理大數據集。因此，在數據量大的情況下，我們需要使用分布式訓練：Spark中的邏輯回歸或交替方向乘子法（ADMM）。

Apache Spark

Apache Spark是一個強大的分布式數據處理工具。它可以用于在集群上的多臺機器上并行訓練邏輯回歸模型。

交替方向乘子法（ADMM）

ADMM是一種優化技術，它將問題分解為可以并行解決的較小子問題。這對于需要機器之間協調的分布式環境特別有用。

結論

邏輯回歸是一種強大且高效的二分類方法，特別適用于稀疏特征和大數據集。通過利用如Apache Spark的分布式訓練框架和ADMM等優化技術，邏輯回歸可以擴展以應對現代數據科學應用的需求。

邏輯回歸與對數幾率

概率與幾率

概率 §：事件發生的可能性。
幾率：事件發生的概率與其不發生的概率之比。

$\text{幾率} = \frac{P}{1 - P}$

對數幾率（Logit）

對數幾率是幾率的自然對數。

$\text{對數幾率} = \log \left( \frac{P}{1 - P} \right)$

邏輯回歸模型

在邏輯回歸中，事件發生概率的對數幾率（例如點擊的概率）被建模為輸入特征的線性組合。
模型方程為：

$\log \left( \frac{P}{1 - P} \right) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \ldots + \theta_n x_n$
這里， $\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \ldots + \theta_n x_n$ 是特征的線性組合，通常表示為 $z$ 。

連接 ( z ) 和對數幾率

術語 $\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \ldots + \theta_n x_n$ 代表邏輯回歸模型中的對數幾率。盡管 $z$ 本身不包含對數，它是邏輯函數的參數，將其映射到概率。

邏輯回歸中代價函數的梯度

邏輯回歸中代價函數 $J(\theta)$ 對參數 $\theta$ 的梯度為：

$\frac{\partial J(\theta)}{\partial \theta} = x^{(i)} (h_\theta(x^{(i)}) - y^{(i)})$

這個公式來自于為二分類問題的邏輯回歸代價函數導出的梯度。

推導

讓我們一步步推導這個公式。

1. 假設函數

在邏輯回歸中，假設函數 $h_\theta(x)$ 由應用于輸入特征線性組合的S型函數給出：

$h_\theta(x) = \sigma(\theta^T x) = \frac{1}{1 + e^{-\theta^T x}}$

2. 代價函數

邏輯回歸的代價函數是訓練數據的負對數似然，可以寫為：

$J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right]$

3. 簡化代價函數

為了簡便起見，我們關注于單個訓練樣本 $x^{(i)}, y^{(i)})$ 的代價函數：

$J(\theta) = -\left[ y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right]$

4. 對 $\theta_j$ 的偏導數

為了找到梯度，我們需要計算 $J(\theta)$ 對每個參數 $\theta_j$ 的偏導數。我們將 $\theta^T x^{(i)}$ ，因此 $h_\theta(x^{(i)}) = \sigma(z)$ 。

代價函數 $J(\theta)$ 對 $\theta_j$ 的偏導數為：

$\frac{\partial J(\theta)}{\partial \theta_j} = -\left[ \frac{\partial}{\partial \theta_j} y^{(i)} \log(h_\theta(x^{(i)})) + \frac{\partial}{\partial \theta_j} (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right]$

使用鏈式法則，我們有：
$\frac{\partial}{\partial \theta_j} h_\theta(x^{(i)}) = \frac{\partial \sigma(z)}{\partial z} \cdot \frac{\partial z}{\partial \theta_j} = \sigma(z) (1 - \sigma(z)) \frac{\partial z}{\partial \theta_j} = h_\theta(x^{(i)}) (1 - h_\theta(x^{(i)})) x_j^{(i)}$

5. 每項的導數

現在，計算代價函數中每項的偏導數：

$\frac{\partial}{\partial \theta_j} y^{(i)} \log(h_\theta(x^{(i)})) = y^{(i)} \frac{1}{h_\theta(x^{(i)})} \frac{\partial h_\theta(x^{(i)})}{\partial \theta_j} = y^{(i)} \frac{1}{h_\theta(x^{(i)})} h_\theta(x^{(i)}) (1 - h_\theta(x^{(i)})) x_j^{(i)} = y^{(i)} (1 - h_\theta(x^{(i)})) x_j^{(i)}$

$\frac{\partial}{\partial \theta_j} (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) = (1 - y^{(i)}) \frac{1}{1 - h_\theta(x^{(i)})} \frac{\partial (1 - h_\theta(x^{(i)})}{\partial \theta_j} = (1 - y^{(i)}) \frac{1}{1 - h_\theta(x^{(i)})} (-h_\theta(x^{(i)})) x_j^{(i)} = - (1 - y^{(i)}) h_\theta(x^{(i)}) x_j^{(i)}$

6. 合并項

合并這些結果：

$\frac{\partial J(\theta)}{\partial \theta_j} = - \left[ y^{(i)} (1 - h_\theta(x^{(i)})) x_j^{(i)} + (1 - y^{(i)}) (- h_\theta(x^{(i)})) x_j^{(i)} \right]$

$\frac{\partial J(\theta)}{\partial \theta_j} = - \left[ y^{(i)} x_j^{(i)} - y^{(i)} h_\theta(x^{(i)})) x_j^{(i)} - (1 - y^{(i)}) h_\theta(x^{(i)})) x_j^{(i)} \right]$

$\frac{\partial J(\theta)}{\partial \theta_j} = - \left[ y^{(i)} x_j^{(i)} - h_\theta(x^{(i)})) x_j^{(i)} \right]$

$\frac{\partial J(\theta)}{\partial \theta_j} = x_j^{(i)} (h_\theta(x^{(i)}) - y^{(i)})$

向量形式

用向量形式表達所有參數：

$\nabla_\theta J(\theta) = x^{(i)} (h_\theta(x^{(i)}) - y^{(i)})$

其中：

$x^{(i)}$ 是第i個樣本的特征向量。
$h_\theta(x^{(i)})$ 是第i個樣本的預測概率。
$y^{(i)}$ 是第i個樣本的實際標簽。

總結

邏輯回歸中代價函數的梯度為：

$\frac{\partial J(\theta)}{\partial \theta} = x^{(i)} (h_\theta(x^{(i)}) - y^{(i)})$

這個梯度告訴我們如何調整模型參數 $\theta$ 來最小化代價函數，這是梯度下降優化中訓練邏輯回歸模型的關鍵組成部分。

代碼實現

def dJ(theta, X, y, i):return np.array(X[i]) * (-y[i] + sigmoid(np.matmul(np.array(X[i]), theta)))def train(theta, X, y, num_epoch, learning_rate):for num_epoch in range(int(num_epoch)):for i in range(len(X)):theta -= float(learning_rate) * dJ(theta, X, y,i )return thetadef predict(update_theta, X):y_pred = []for i in range(len(X)):if sigmoid(np.matmul(X[i], update_theta)) >= 0.5:y_pred.append(1)else:y_pred.append(0)return y_pred