大俠幸會，在下全網同名「算法金」 0 基礎轉 AI 上岸，多個算法賽 Top 「日更萬日，讓更多人享受智能樂趣」

抱個拳，送個禮

1. 方差

方差是統計學中用來度量一組數據分散程度的重要指標。它反映了數據點與其均值之間的偏離程度。在數據分析和機器學習中，方差常用于描述數據集的變異情況

1.1 定義與計算方法 方差的計算方法如下：

1. 計算數據集的均值（平均值）
2. 計算每個數據點與均值的差值
3. 將這些差值平方
4. 將平方后的差值相加
5. 將總和除以數據點的數量

方差的公式為：

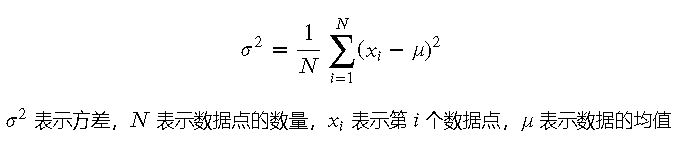
1.2 實際應用 方差在許多領域都有廣泛應用。例如，在金融領域，方差用來衡量投資回報率的波動性。在質量控制中，方差用來衡量生產過程的穩定性。在機器學習中，方差用于評估模型的性能和穩定性

1.3 示例

假設我們有一組數據：[1, 2, 3, 4, 5]

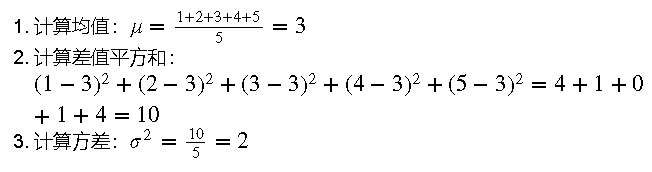
2. 標準差

標準差是方差的平方根，是另一種度量數據分散程度的指標。標準差與方差一樣，反映了數據點與均值之間的偏離程度，但標準差的單位與數據本身一致，因此更容易解釋和理解

2.1 定義與計算方法 標準差的計算方法如下：

1. 計算數據集的均值（平均值）
2. 計算每個數據點與均值的差值
3. 將這些差值平方
4. 將平方后的差值相加
5. 將總和除以數據點的數量，得到方差
6. 對方差取平方根，得到標準差

標準差的公式為：

2.2 實際應用 標準差廣泛應用于各種領域。例如，在金融領域，標準差用來衡量投資回報率的波動性。在質量控制中，標準差用來衡量生產過程的穩定性。在統計分析和數據科學中，標準差用來描述數據集的離散程度

2.3 示例

繼續前面的例子，假設我們有一組數據：[1, 2, 3, 4, 5]

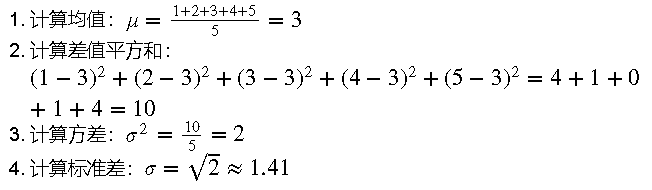
防失聯，進免費知識星球，直達算法金 AI 實驗室 https://t.zsxq.com/ckSu3

更多內容，見免費知識星球

3. 協方差

協方差是用來衡量兩個變量之間關系的一種統計指標。它表示了兩個變量如何一起變化：當一個變量變大時，另一個變量是否也變大（正協方差）或變小（負協方差）。協方差的值可以是正、負或零，具體取決于變量之間的關系

3.1 定義與計算方法 協方差的計算方法如下：

1. 計算每個變量的均值（平均值）
2. 計算每個變量與其均值的差值
3. 將兩個變量的差值乘積求和
4. 將和除以數據點的數量

協方差的公式為：

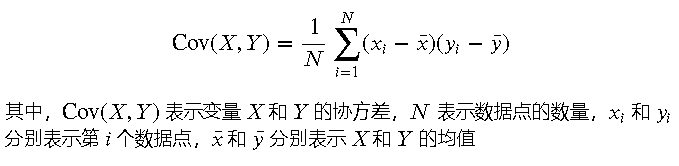
3.2 實際應用 協方差在許多領域都有廣泛應用。例如，在金融領域，協方差用來衡量不同資產回報率之間的相關性。在經濟學中，協方差用來分析不同經濟指標之間的關系。在機器學習中，協方差用于特征選擇和數據預處理

3.3 示例

假設我們有兩個變量的數據集：𝑋=[1,2,3,4,5]𝑋=[1,2,3,4,5] 和 𝑌=[2,4,6,8,10]

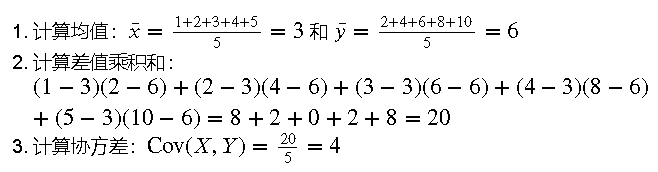
抱個拳，送個禮

點擊 ↑ 領取

4. 協方差矩陣

協方差矩陣是用于描述多個變量之間協方差關系的矩陣。它是一個對稱矩陣，其中每個元素表示對應變量對之間的協方差。協方差矩陣在多變量統計分析和機器學習中起著重要作用

4.1 定義與計算方法 協方差矩陣的計算方法如下：

1. 計算每個變量的均值（平均值）
2. 計算每個變量與其均值的差值
3. 計算每對變量之間的協方差
4. 將協方差填入矩陣對應位置

協方差矩陣的公式為：

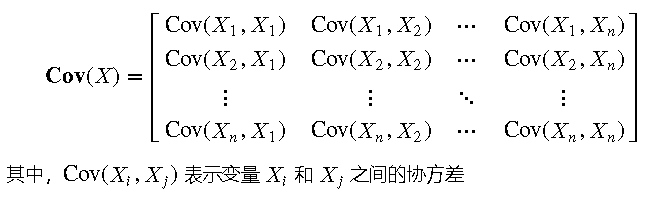
4.2 實際應用 協方差矩陣在數據分析和機器學習中有廣泛的應用。例如，在主成分分析（PCA）中，協方差矩陣用于特征降維。在多變量回歸分析中，協方差矩陣用于估計回歸系數的標準誤。在組合投資中，協方差矩陣用于分析不同資產的風險

4.3 示例

假設我們有三個變量的數據集：𝑋1=[1,2,3]，𝑋2=[4,5,6]，𝑋3=[7,8,9]

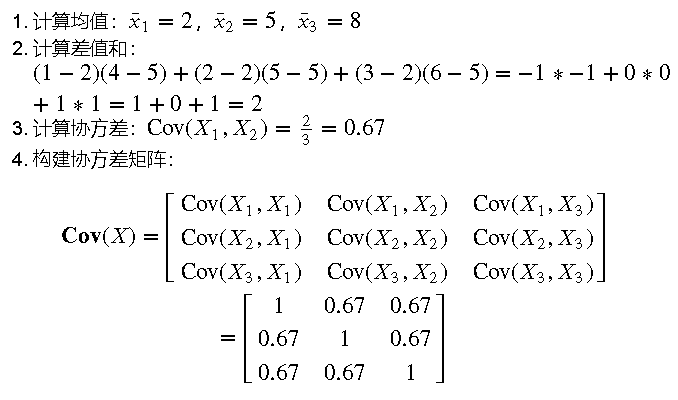
防失聯，進免費知識星球，直達算法金 AI 實驗室

https://t.zsxq.com/ckSu3

5. 各指標之間的關系與對比

在數據分析和統計學中，方差、標準差、協方差及協方差矩陣都是衡量數據分布和變量關系的重要工具。理解它們之間的關系和區別有助于更好地應用這些工具進行分析

5.1 方差與標準差 方差和標準差都是度量數據分散程度的指標，但它們的單位和解釋不同

• 方差：方差表示數據點與均值之間的平方差的平均值，單位是數據單位的平方。方差公式為：

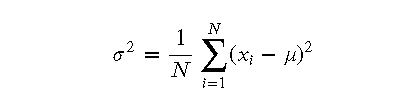
• 標準差：標準差是方差的平方根，因此其單位與數據本身一致。標準差公式為：

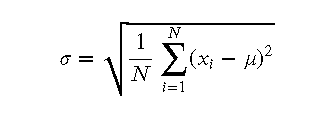
5.2 標準差與協方差 標準差和協方差雖然都是度量數據分布和關系的指標，但它們用于不同的情景

• 標準差：標準差用于度量單個變量的分散程度，是方差的平方根。它可以幫助我們理解單個變量的波動性
• 協方差：協方差用于度量兩個變量之間的關系，表示一個變量變化時另一個變量的變化情況。協方差公式為：

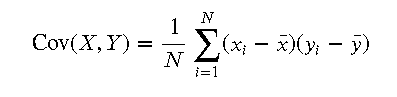
5.3 協方差與協方差矩陣 協方差和協方差矩陣都是用來描述變量之間關系的工具，但協方差矩陣可以同時描述多個變量之間的關系

• 協方差：協方差只描述兩個變量之間的關系，正值表示正相關，負值表示負相關
• 協方差矩陣：協方差矩陣是一個對稱矩陣，包含多個變量之間的協方差信息，用于多變量統計分析。協方差矩陣公式為：

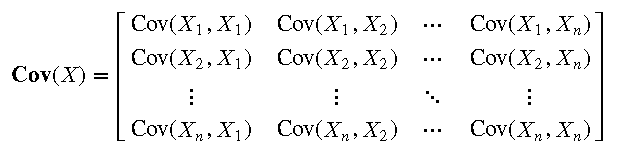
[ 抱個拳，總個結 ]

- 科研為國分憂，創新與民造福 -

日更時間緊任務急，難免有疏漏之處，還請大俠海涵 內容僅供學習交流之用，部分素材來自網絡，侵聯刪

[ 算法金，碎碎念 ]

入選 CSDN 算法領域

內容榜單 Top 1

真香~

全網同名，日更萬日，讓更多人享受智能樂趣

如果覺得內容有價值，煩請大俠多多 分享、在看、點贊，助力算法金又猛又持久、很黃很 BL 的日更下去；同時邀請大俠 關注、星標 算法金，圍觀日更萬日，助你功力大增、笑傲江湖