Kruskal算法求出最小生成樹。

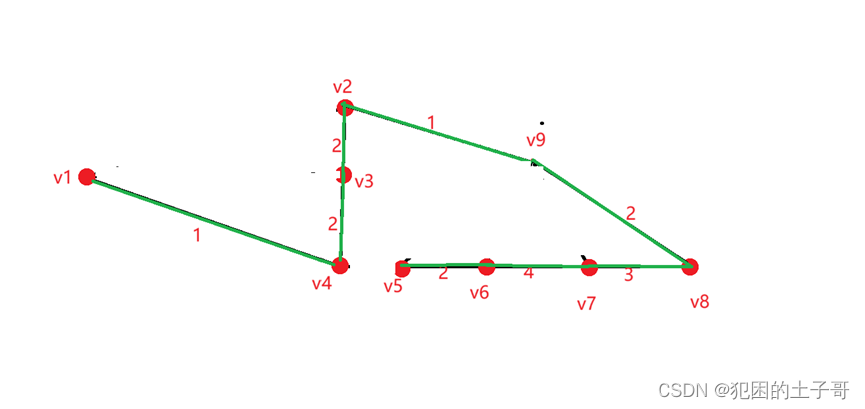
圖形

---

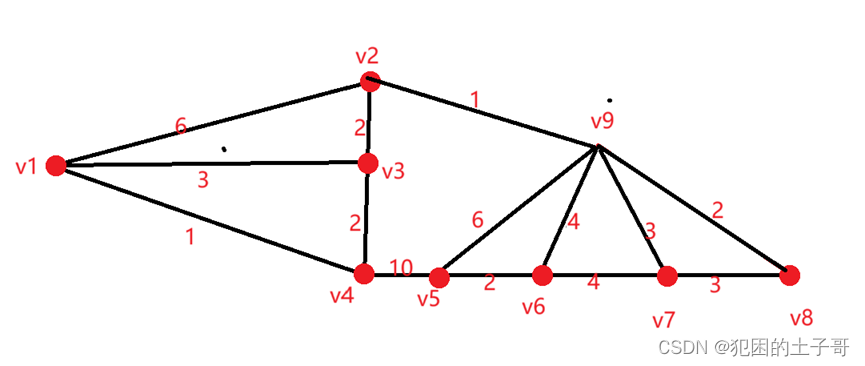
算法描述

先找最小權值邊為1的邊有（V1，V4），（V2，V9），保證不產生回路就可以成功選擇邊

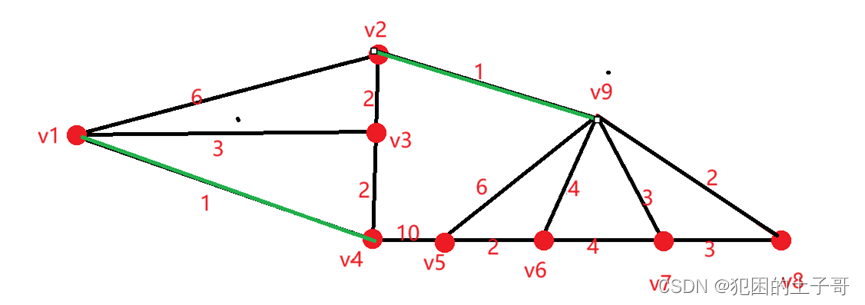
除去上一次找的邊后，在找權值最小的邊為2的有（V2，V3）,（V4，V3），（V5，V6），（V9，V8），連接不產生回路的邊

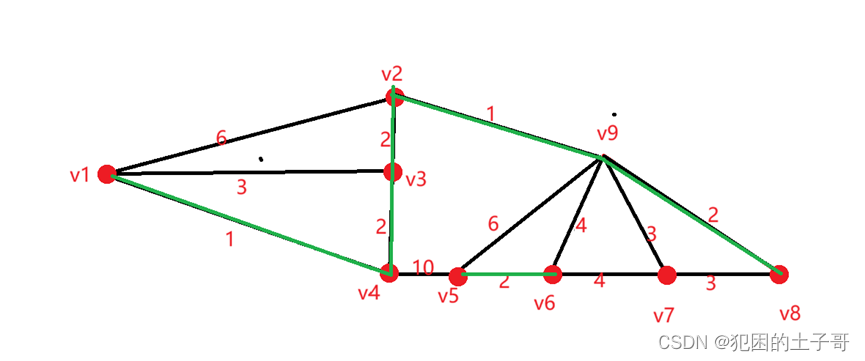
除去之前找過的邊，后面再看權值最小的邊為3的邊有（V1，V3），（V7，V8），（V9，V7）
按順序判斷（V1，V3）邊會產生回路排除，（V7，V8）可選邊，當連接完（V7,V8）后判斷（V9，V7）連接會造成回路排除

排除找過的邊后，找下一個權值最小的為4的邊有（V6,V7），（V9，V6）
順序判斷，（ V6，V7）符合，連接完（V9，V6）判斷連接（V9，V6）是回路不符合

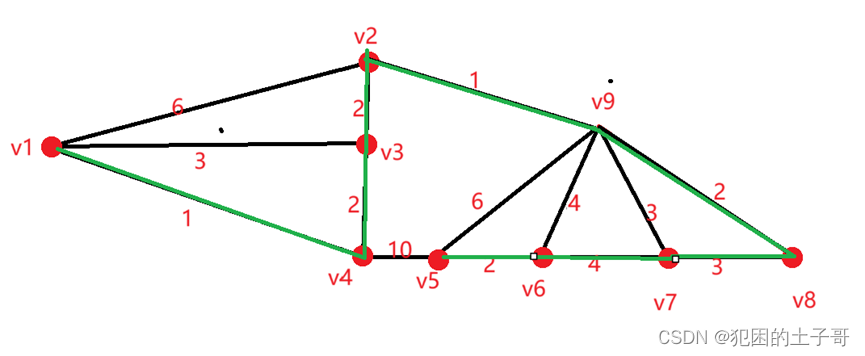
完成所以點相連結束
有N個點，最小生成樹有N-1個邊

---

C語言Kruskal算法實現

//C語言Kruskal算法實現
#include<stdio.h>
#define M 1000//M表示無窮用1000代替
#define N 9 //N行N列的矩陣void loop(int arr[N][N],int dot,int c[N],int* count)
{int i;c[*count] = dot;*count = *count + 1;for ( i = 0; i < N; i++){if (arr[dot][i] == 1){ int flage = 1;for (int j = 0; j < *count; j++){if (i == c[j]){flage = 0;break;}}if(flage){ loop(arr, i, c,count);}}}
}
//標記和判斷是否為回路,不是回路返回1，是回路反回0
int Is(int arr[N][N], int row, int column)
{if (arr[row][column] == 0 || arr[column][row] == 0){int a[N] = { 0 };int b[N] = { 0 };loop(arr, row, a);loop(arr, column, b);int flag = 1;for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){if (a[i] == b[j] && a[i] !=0)flag = 0;}}//沒產生回路標記1if(flag){ arr[row][column] = 1;arr[column][row] = 1;return 1;}//產生回路標記-1	else{arr[row][column] = -1;arr[column][row] = -1;	}}return 0;
}
int main()
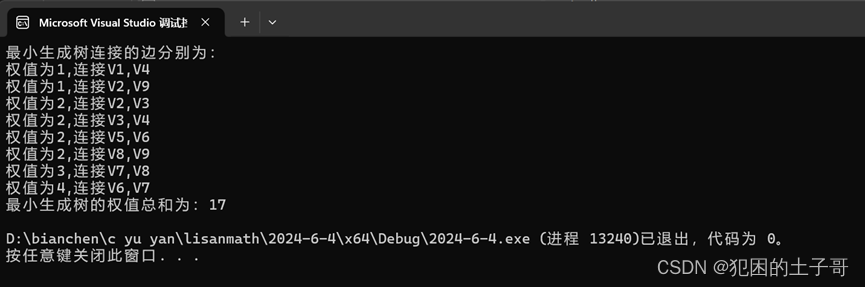
{//把上圖權值對應值寫成鄰接陣int map[N][N] ={{M,6,3,1,M,M,M,M,M},{6,M,2,M,M,M,M,M,1},{3,2,M,2,M,M,M,M,M},{1,M,2,M,10,M,M,M,M},{M,M,M,10,M,2,M,M,6},{M,M,M,M,2,M,4,M,4},{M,M,M,M,M,4,M,3,3},{M,M,M,M,M,M,3,M,2},{M,1,M,M,6,4,3,2,M}};int arr[N][N] = { 0 };//用來標記邊int count = 0;//用來記錄邊的數量,最小生成樹的邊為數N-1int i = 0, j = 0;int min = M;//記錄最小權值int value = 0;//當前要找的最小權值int sum = 0;//記錄總權值//打印printf("最小生成樹連接的邊分別為：\n");while (1){min = M;//每次把最小權設置為最大//找權值最小邊，和最小權值邊的數量for (i = 0; i < N; i++){for (j = 0; j < N; j++){if (map[i][j] < min && map[i][j] > value)//判斷是否為最小權{min = map[i][j];}}}value = min;//根據前面循環得到最小權值邊，標記不構成回路的邊for (i = 0; i < N; i++){for (j = 0; j < N; j++){if (map[i][j] == min && Is(arr, i, j)){//打印printf("權值為%d,連接V%d,V%d\n", value, i + 1, j + 1);sum += min;count++;if (count == (N - 1))break;}}if (count == (N - 1))break;}//找夠邊數跳出循環if (count == (N - 1))break;}printf("最小生成樹的權值總和為：%d\n",sum);return 0;
}