目錄

前言

🎂搜索插入位置

🌼搜索二維矩陣

🌼排序數組元素第一和最后一個位置

🌼旋轉排序數組

💪旋轉排序數組中的最小值

💪兩個正序數組的中位數

---

前言

二分算法學習_時間超限ac:0%-CSDN博客

🎂搜索插入位置

35. 搜索插入位置 - 力扣（LeetCode）

直接套博客里的萬能模板不太行，萬能模板只能處理下取整死循環的問題，但是本題：

目標值 target 不一定在數組里

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int l = 0, r = nums.size() - 1;while (l <= r) {int m = (l + r) >> 1;if (target > nums[m])l = m + 1;else if (target < nums[m])r = m - 1;else {l = m;break;}}// 因為 l<=r 退出循環后, r 必然位于插入位置return l;}
};

🌼搜索二維矩陣

74. 搜索二維矩陣 - 力扣（LeetCode）

1）別混淆 mid 和 m，此處 m 是 m 行，mid 才是中間值

2）對第 3 種情況，target == matrix[][]，進行處理

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int m = matrix.size(), n = matrix[0].size();int l = 0, r = m*n - 1; // 二維轉一維while (l < r) {int mid = (l + r + 1) >> 1;if (target > matrix[mid/n][mid%n]) // 一維轉二維l = mid;else if (target < matrix[mid/n][mid%n])r = mid - 1;else {l = mid;break;}}return matrix[l/n][l%n] == target;}
};

🌼排序數組元素第一和最后一個位置

34. 在排序數組中查找元素的第一個和最后一個位置 - 力扣（LeetCode）

1）利用 while (l <= r) { ... l = m + 1 ... r = m - 1?};? 左閉右閉區間

退出循環時，l 的位置就是 >= target 的最小的數

r == l - 1

2）只需求出第一個位置，即可取巧得到最后一個位置，現在有二分函數 lowerbound(nums, target) 得到第一個位置，最后一個位置即 lowerbound(nums, target + 1) - 1

3）奇數個元素，m = (l + r) / 2，取到中間的元素；偶數個元素，因為整數默認下取整，會取中間兩個元素左邊那個

坑：

1）不要用 >> 1，要用 / 2，不知道力扣是不是不支持位移運算符（>> 1 會超出時間限制）?

2）如果想要從 r = m - 1 開始，那么最后應該 return r;? ?r 此時位于最后一個位置（詳情看代碼 2）（用例1模擬一下）

代碼 1

class Solution {
public:// >= target 的最小的數的位置int lowerbound(vector<int>& nums, int target) {int l = 0, r = nums.size() - 1;while (l <= r) {int m = l + (r - l) / 2;if (target > nums[m])l = m + 1;elser = m - 1;}return l; // 第一個位置}vector<int> searchRange(vector<int>& nums, int target) {int start = lowerbound(nums, target);if (start >= nums.size() || nums[start] != target)return {-1, -1};int end = lowerbound(nums, target + 1) - 1;return {start, end};}
};

代碼 2

class Solution {
public:// >= target 的最小的數的位置int lowerbound(vector<int>& nums, int target) {int l = 0, r = nums.size() - 1;while (l <= r) {int m = l + (r - l) / 2;if (target < nums[m])r = m - 1;elsel = m + 1;}return r; // 最后一個位置}vector<int> searchRange(vector<int>& nums, int target) {int end = lowerbound(nums, target);if (end < 0 || nums[end] != target)return {-1, -1};int start = lowerbound(nums, target - 1) + 1;return {start, end};}
};

🌼旋轉排序數組

33. 搜索旋轉排序數組 - 力扣（LeetCode）

1）二分時，套 while (l <= r) 的模板，mid 位于中間 OR 中間偏左位置

此時，[l, mid] OR [mid + 1, r]，至少一個區間是有序的，所以對左右區間的有序分類討論

class Solution {
public:int search(vector<int>& nums, int target) {int n = nums.size();int l = 0, r = n - 1;// 二分找到 k 的位置while (l <= r) {int mid = (l + r) / 2;// target 位于 midif (nums[mid] == target)return mid;// 左邊有序else if (nums[l] <= nums[mid]) {// target 位于左邊（不包括 mid）if (nums[l] <= target && target < nums[mid]) r = mid - 1;else l = mid + 1;}// 右邊有序else {// target 位于右邊（不包括 mid）if (nums[mid] < target && target <= nums[r])l = mid + 1;elser = mid - 1;}}return -1; // 未找到}
};

💪旋轉排序數組中的最小值

153. 尋找旋轉排序數組中的最小值 - 力扣（LeetCode）

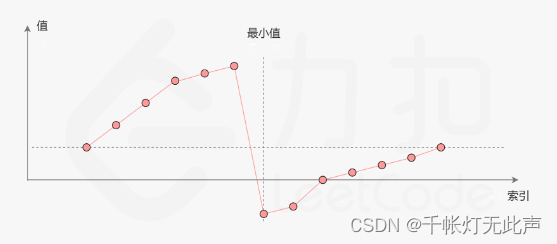
上一題是找目標值，本題是找最小值（都滿足部分有序）

本題每次旋轉，將最后一個值提取到最前面

可以畫幾個例子多驗證一下：2 0 1，1 2 0，3 4 5 2，5 2 3 4

最小值處于斷崖的第一個位置，顯而易見，肯定位于無序一邊

所以每次壓縮有序部分，到無序部分找，注意結合例子處理邊界

class Solution {
public:int findMin(vector<int>& nums) {int n = nums.size();int l = 0, r = n - 1;while (l <= r) { // l < r 也行// 單調升序if (nums[l] <= nums[r]) // 用 = 防止單個元素時死循環return nums[l];int m = (l + r) / 2;// 左邊有序if (nums[m] >= nums[l]) // 用 = 防止 r 跳過最小值l = m + 1; // 去右邊找elser = m; // 不用 m-1 防止跳過最小值}return nums[l];}
};

💪兩個正序數組的中位數

4. 尋找兩個正序數組的中位數 - 力扣（LeetCode）

結合這篇博客理解一下，用刪除（淘汰）的思路
尋找兩個正序數組的中位數（292） | 小浩算法 (geekxh.com)

輔助數組 findKth(nums1, i, nums2, j, k)，i, j 是兩個數組起始索引，第 k 大元素

如果第一個數組起始位置 i + 2/k - 1 的值 < 第二個數組起始位置 j + 2/k - 1 的值

那么就淘汰掉第一個數組前 2/k 個元素，反之淘汰另一個數組前 2/k 個元素

直到 k == 1，此時比較兩個數組起始第 1 個元素大小即可

；

或者一個數組為空（即 i >= nums1.size() 或 j >= nums2.size()）

時間 O(log( max(m, n) ))

class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int n = nums1.size(), m = nums2.size();int left = (n + m + 1) / 2, right = (n + m + 2) / 2; // 中間值索引 left 和 rightreturn (findKth(nums1, 0, nums2, 0, left) + findKth(nums1, 0, nums2, 0, right)) / 2.0;}// nums1 起始索引 i, nums2 起始索引 j, 返回合并數組 第 k 個元素（1開始算）int findKth(vector<int>& nums1, int i, vector<int>& nums2, int j, int k) {if (i >= nums1.size()) // nums1 空數組return nums2[j + k - 1];if (j >= nums2.size()) // nums2 空數組return nums1[i + k - 1];if (k == 1)return min(nums1[i], nums2[j]); // 返回較小值// 2/k 位置的值// 如果一個數組 k/2 處超出范圍, 無法判斷中位數是否位于這個數組// 但是另一個數組前 k/2 個肯定沒有中位數// 取 MAX, 淘汰另一個數組前 k/2 個元素int mid1 = (i + k/2 - 1 < nums1.size()) ? nums1[i + k/2 - 1] : INT_MAX;int mid2 = (j + k/2 - 1 < nums2.size()) ? nums2[j + k/2 - 1] : INT_MAX;// 遞歸二分if (mid1 < mid2) // mid1 淘汰 k/2return findKth(nums1, i + k/2, nums2, j, k - k/2);else // mid2 淘汰 k/2return findKth(nums1, i, nums2, j + k/2, k - k/2);}
};