題意
整數數組 nums 按升序排列,數組中的值 互不相同 。
在傳遞給方法之前,nums 在預先未知的某個下標 k(0 <= k < nums.length)上進行了旋轉,使數組變為 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下標 從 0 開始計數)。例如, [0,1,2,4,5,6,7] 在下標 3 處經旋轉后可能變為 [4,5,6,7,0,1,2] 。
給你旋轉后的數組 nums 和一個整數 target,如果 nums 中存在這個目標值 target,則返回它的下標,否則返回 -1 。
你必須設計一個時間復雜度為 O(log n) 的算法解決此問題。
難度
中等
示例
輸入:nums = [4,5,6,7,0,1,2], target = 0
輸出:4輸入:nums = [4,5,6,7,0,1,2], target = 3
輸出:-1分析 1
這道題咋眼一看,有點繞,給一個旋轉后的數組,和一個目標值,并要求我們找到這個目標值的下標。
但稍微分析一下就知道,就是在一個數組當中查找一個目標值,如果不考慮時間復雜度的話,我們可以直接遍歷一遍,找到就返回下標,找不到就返回-1。
超級簡單:
class Solution {public int search(int[] nums, int target) {for(int i = 0;i < nums.length;i++){if(nums[i] == target)return i;}return -1;}
}來看一下效率:
效率不錯,但要時間復雜度為對數級別。那就要考慮別的算法
分析 2
我們知道,在一個有序的數組里面去判斷一個數是否存在,可以利用二分查找,時間復雜度剛好就是$O(\log{n})$。
但這道題只是部分有序(因為旋轉了),該怎么去判斷呢?
閉上眼,想一下。
從任意位置將這個部分有序的數組分開,那么分開之后的兩部分必然有一部分是有序的!
比如:
nums = [4,5,6,7,0,1,2]
nums = [4] [5,6,7,0,1,2] breakPos = 1
nums = [4,5] [6,7,0,1,2] breakPos = 2
nums = [4,5,6] [7,0,1,2] breakPos = 3
nums = [4,5,6,7] [0,1,2] breakPos = 4
nums = [4,5,6,7,0] [1,2] breakPos = 5
nums = [4,5,6,7,0,1] [2] breakPos = 6果然,至少有一部分是有序的。那我們是不是就可以從有序的部分當中去尋找 target 呢?
可以是可以,但時間復雜度并不是 $O(\log{n})$,還要加上 breakPos 分割后無序的部分,合起來就是$O(n + \log{n})$,顯然也不符合題目的要求。
考慮下面的思路:
- 如果[lef,breakPos - 1]是有序的,而且nums[lef] <= target && target < nums[breakPos],那么答案肯定在[lef, breakPos - 1],直接調整上界rig到breakPos - 1。
- 如果[breakPos,rig]是有序的,而且nums[breakPos] < target && target <= nums[rig],那么答案肯定在[breakPos,rig]中,調整下界lef到breakPos即可。
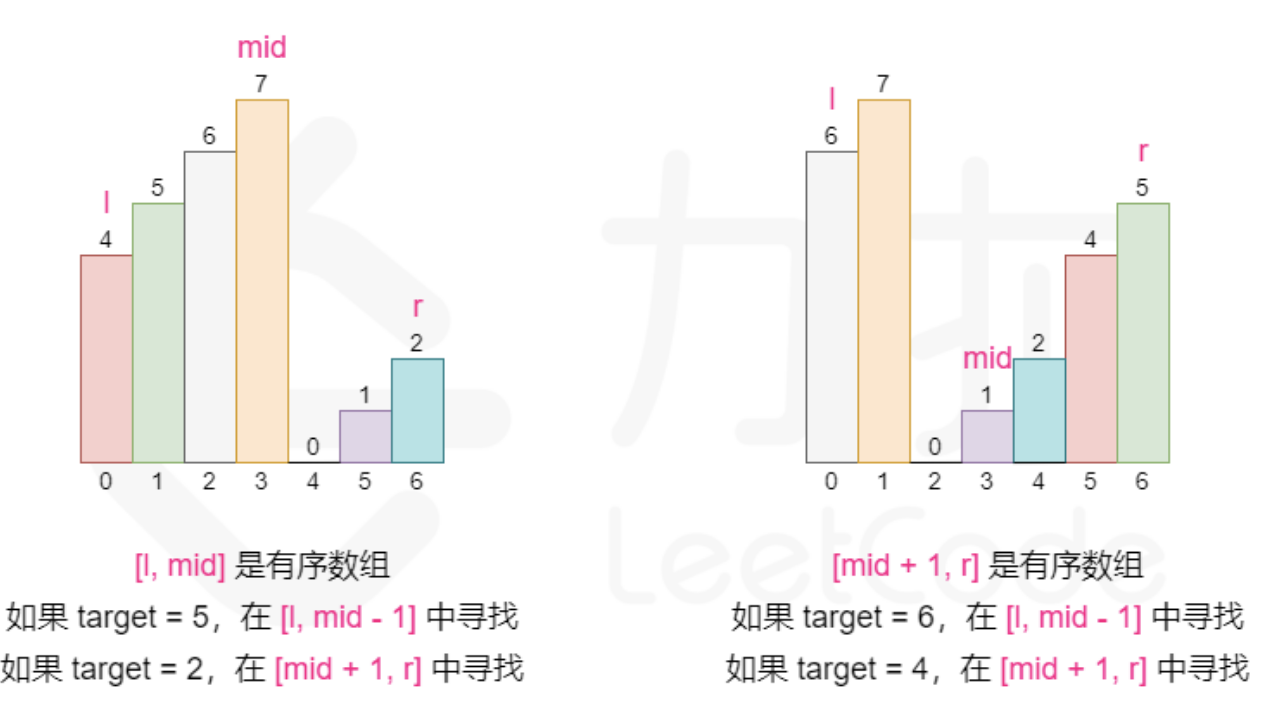
也就是說,我們通過判斷有序的部分,來決定下一步的查找范圍。
- 只有在有序區間內才可以通過區間兩端的數值判斷 target 是否在其中。
- 判斷有序區間還是亂序區間:left <= right 是順序區間,否則亂序區間。
- 每次二分至少存在一個有序區間。
class Solution {public int search(int[] nums, int target) {int siz = nums.length; // 數組長度int lef = 0, rig = siz - 1; // 初始化左右指針while (lef <= rig) { // 當左指針小于等于右指針時進行循環int mid = (lef + rig) >> 1; // 計算中間索引,使用右移運算符相當于除以 2if (nums[mid] == target) // 如果中間元素等于目標值,返回中間索引return mid;if (nums[0] <= nums[mid]) { // 如果左半部分有序if (nums[0] <= target && target < nums[mid]) // 如果目標值在左半部分范圍內rig = mid - 1; // 移動右指針elselef = mid + 1; // 否則移動左指針} else { // 右半部分有序if (nums[mid] < target && target <= nums[siz - 1]) //如果目標值在右半部分范圍內lef = mid + 1; // 移動左指針elserig = mid - 1; // 否則移動右指針}}return -1; // 如果未找到目標值,返回 -1}
}
我們來分析一下代碼的關鍵部分:
第一步,初始化:
- siz:數組長度。
- lef 和 rig:左右指針,分別初始化為數組的第一個和最后一個索引。
第二步,二分查找:
計算中間索引 mid;如果 nums[mid] 等于目標值 target,直接返回 mid。
檢查數組的左半部分是否有序(nums[0] <= nums[mid])。
如果左半部分有序,并且目標值在左半部分范圍內(nums[0] <= target && target < nums[mid]),移動右指針到 mid - 1;否則,移動左指針到 mid + 1。
如果右半部分有序,并且目標值在右半部分范圍內(nums[mid] < target && target <= nums[siz - 1]),移動左指針到 mid + 1;否則,移動右指針到 mid - 1。
第三步,如果循環結束仍未找到目標值,返回 -1。
假設數組為 [4, 5, 6, 7, 0, 1, 2],目標值 target 為 0,我們來模擬一下整個題解過程:
- 1.初始 lef = 0,rig = 6,mid = 3,nums[mid] = 7。
- 2.nums[0] <= nums[mid],左半部分有序。
- 3. 0 不在左半部分范圍內,移動左指針 lef = 4。
- 4.更新 mid = 5,nums[mid] = 1。
- 5.nums[4] <= nums[mid],右半部分有序。
- 6. 0 在右半部分范圍內,移動右指針 rig = 5。
- 7.更新 mid = 4,nums[mid] = 0,找到目標值,返回 4。
總結
遇到 O(log n) 的題目,首先想到的就是二分查找,這道題也是一樣,只不過在二分查找的基礎上,增加了一些判斷條件。而二分查找的關鍵是找到有序的部分。
力扣鏈接:. - 力扣(LeetCode)












)






)