基礎
空間域與變換域
空間域:認為是圖像本身,對于空間域的操作就是對圖像中的像素直接進行修改
變換域:變換系數處理,不直接對于圖像的像素進行處理
鄰域
圖像中某點的鄰域被認為是包含該點的小區域,也被稱為窗口
空間濾波
鄰域選擇空間域中的一小塊區域,對于鄰域中的像素運用算子T,并在該位置產生一個輸出;隨后將鄰域的原點移動到下一個位置,并且重復前面的過程,生成下一個位置的值,當鄰域的大小為1*1的時候,輸出像素只取決于輸入像素,而與周邊像素無關
灰度變換函數
(1)反轉變換:s = (L-1) - r
r為輸入圖像像素,s為輸出圖像像素,[0,L-1]為圖像的灰度集
作用:使黑白反轉
(2)對數變換: s = c log ? ( 1 + r ) s= c\log(1+r) s=clog(1+r)
c為常數,r>=0,使用對數變換可以讓原圖的灰度進行壓縮,避免超出設備的限制,如圖所示,將較低的灰度提高到了中間,同理還有其他變換函數也能起到相同或者相反的作用
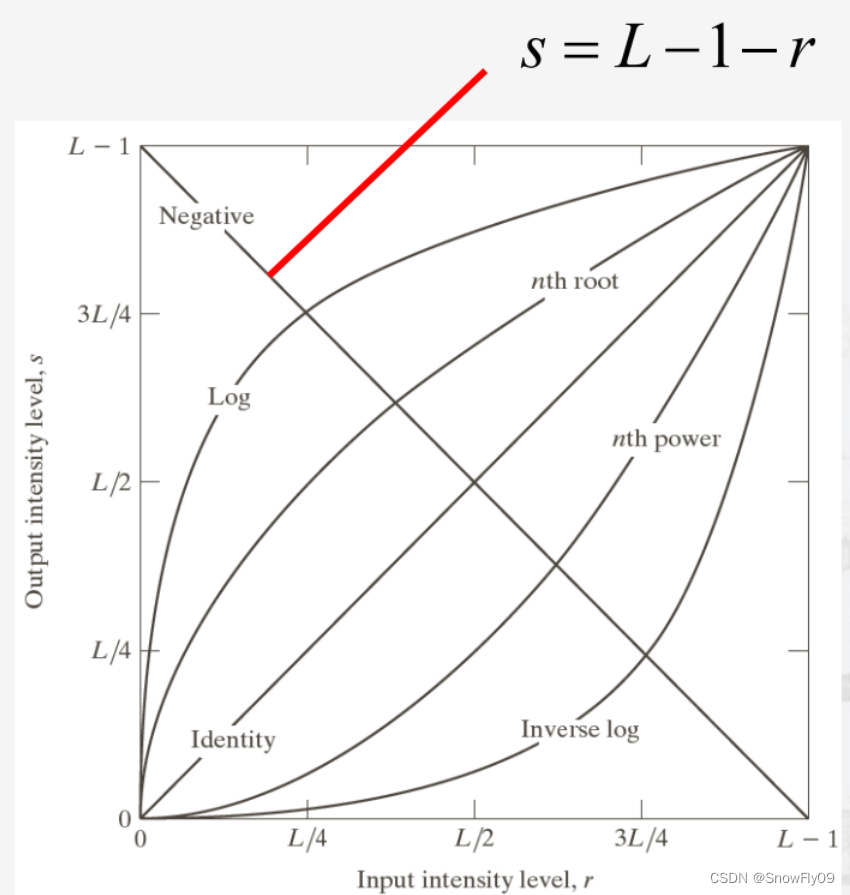
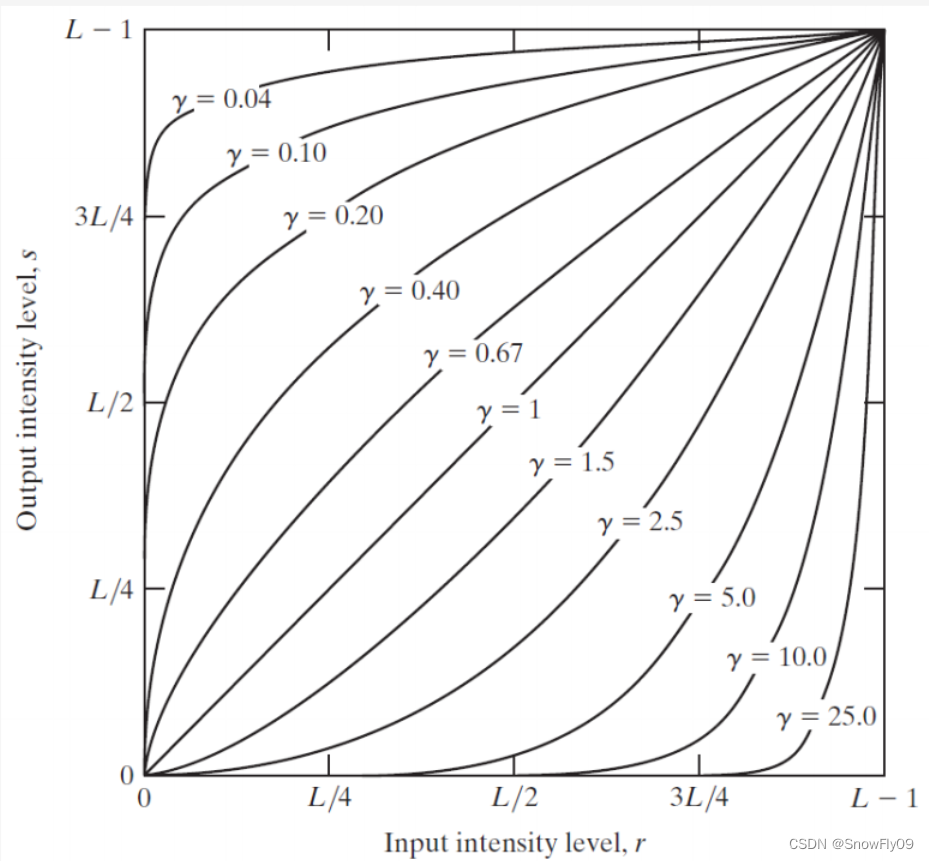
(3)冪變換: s = c ? r γ s=c\cdot r^\gamma s=c?rγ
gamma小于1的時候,提高了灰度級,gamma大于1時,降低了灰度級
(記住圖片就好)
直方圖處理(重要)
對于一個灰度級范圍為[0,L-1]的數字圖像,其直方圖表示為 h ( r k ) = n k h(r_k) = n_k h(rk?)=nk?,其中rk代表著第k級灰度,nk是圖像中處在該灰度級的像素個數
歸一化: p ( r k ) = h ( r k ) / M N p(r_k)=h(r_k)/MN p(rk?)=h(rk?)/MN
p是灰度級在圖像中出現的概率估計,所有分量加起來之和為1
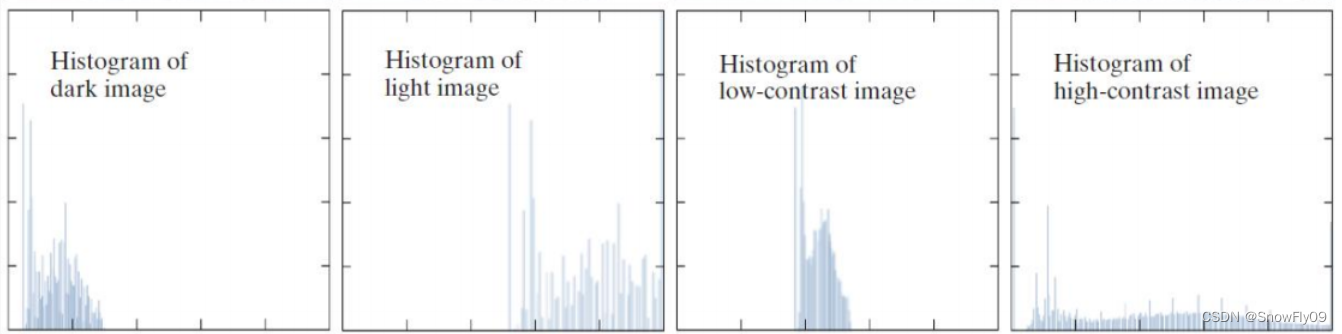
從左至右分別為暗圖片,兩圖片,低對比度圖片,高對比度圖片
直方圖均衡
目的就是將聚集在一起的灰度值變得“平坦”得分布在所有灰度級上,從最終結果上來說可以認為增加了對比度,同時將過亮或者過暗的圖片調整正常。
這里我們不對于直方圖均衡的具體原理進行細究,如想了解清楚請查看此處:直方圖均衡化原理
理想情況下,均衡后的連續函數會使所有灰度級的概率密度全部相等
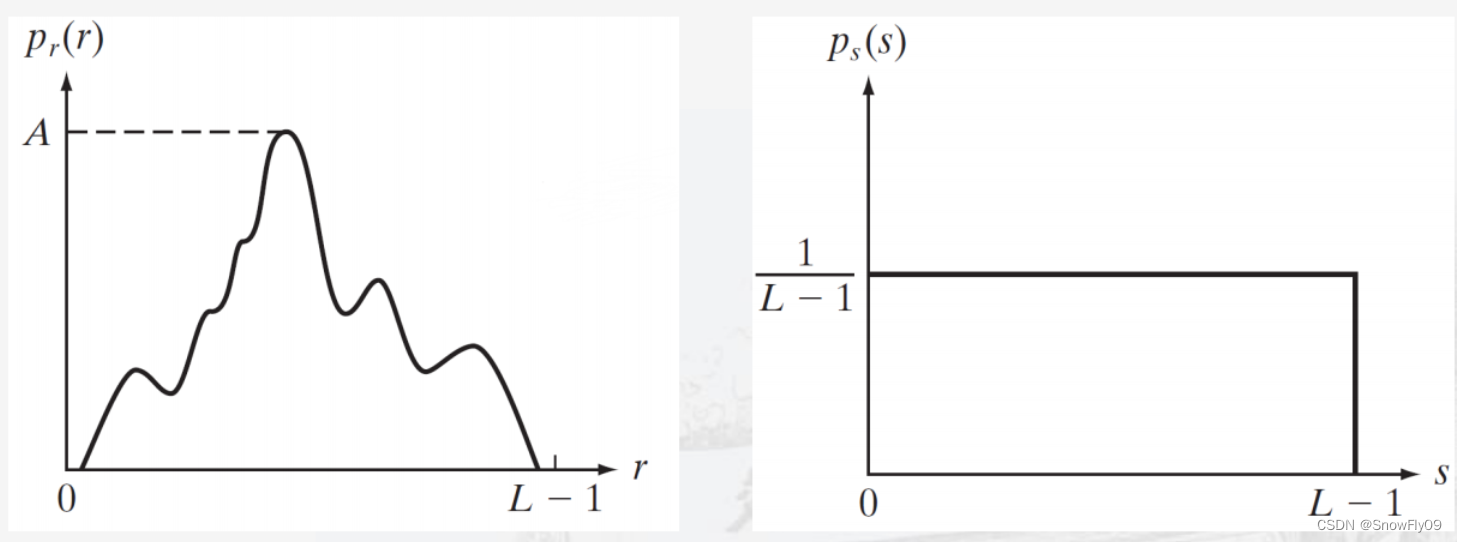
以下為實際遇到時的處理:
(這里也可以跳轉我之前做過的直方圖均衡/匹配實驗,內含matlab代碼:https://blog.csdn.net/weixin_46876169/article/details/137008120?spm=1001.2014.3001.5501)
e.g.一幅圖大小為64*64,其灰度級范圍為[0,7],歸一化的灰度分布如下表所示:
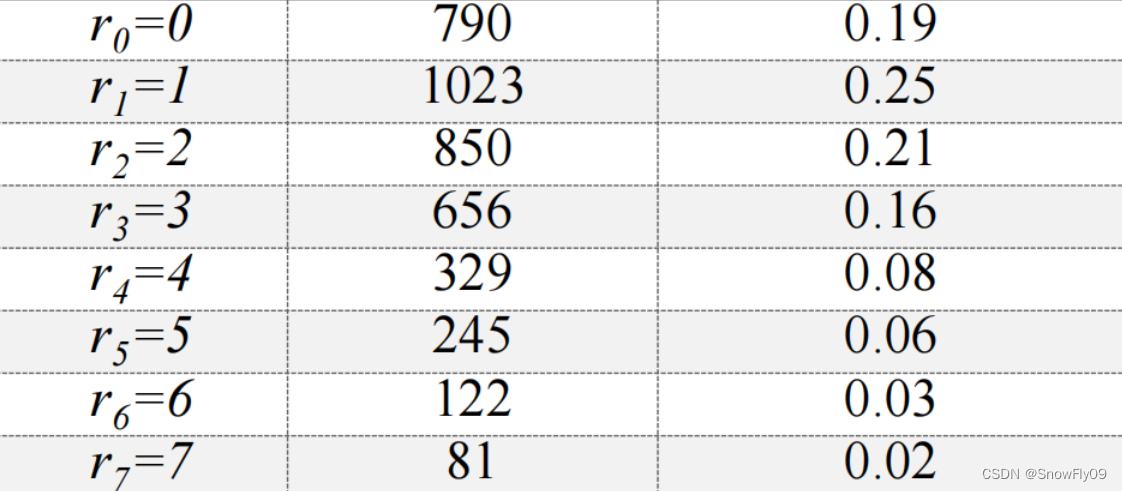
直方圖均衡變換函數為: s k = T ( r k ) = ( L ? 1 ) ∑ j = 0 k p r ( r j ) s_k = T(r_k)=(L-1)\sum\limits_{j=0}^kp_r(r_j) sk?=T(rk?)=(L?1)j=0∑k?pr?(rj?)
可以計算得到: s 0 = 7 × p r ( r 0 ) = 7 ? 0.19 = 1.33 s_0 = 7 \times p_r(r_0) = 7 \cdot 0.19 = 1.33 s0?=7×pr?(r0?)=7?0.19=1.33, s 1 = 7 p r ( r 0 ) + 7 p r ( r 1 ) = 3.08 s_1= 7p_r(r_0) + 7p_r(r_1) = 3.08 s1?=7pr?(r0?)+7pr?(r1?)=3.08,同樣有s2=4.55,s3=5.67,s4=6.23,s5=6.65,s6=6.86,s7=7.00
將這些小數進行取整到最近的整數:
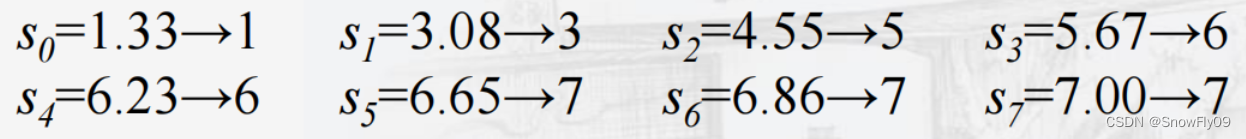
通過這一組式子,我們可以得到映射關系,原本灰度級為0的像素映射到1,灰度級為1的像素映射到3,其他類似
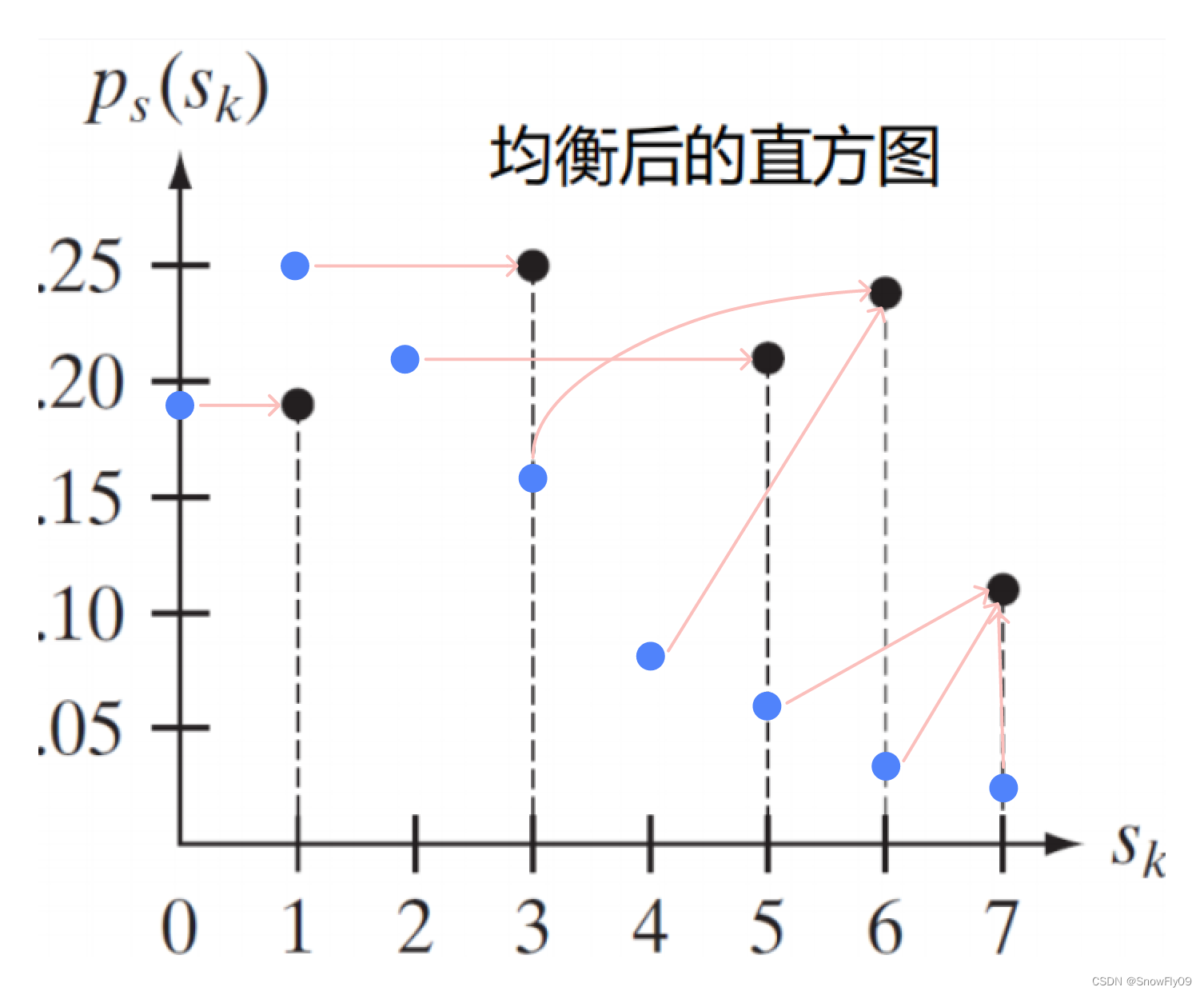
我們可以發現,均衡后的直方圖在亮度上整體有了提高,同時盡可能均勻的平鋪在所有灰度級中
直方圖匹配
有時候直方圖均衡處理完的圖片并不滿足我們需要的效果,比如對于上圖我們只想提高亮度,而不想提高其對比度,那么通過直方圖均衡這樣的方法就沒法做到。此時我們可以選取一張我們希望的亮度與對比度的圖片,使用直方圖匹配的方法來將原直方圖變為我們需要的樣子。
這里我們仍然忽略繁雜的理論推導,直接來看一看具體的例子,假設變換對象仍然為原來的圖片,新的參考圖的直方圖給在了圖中:
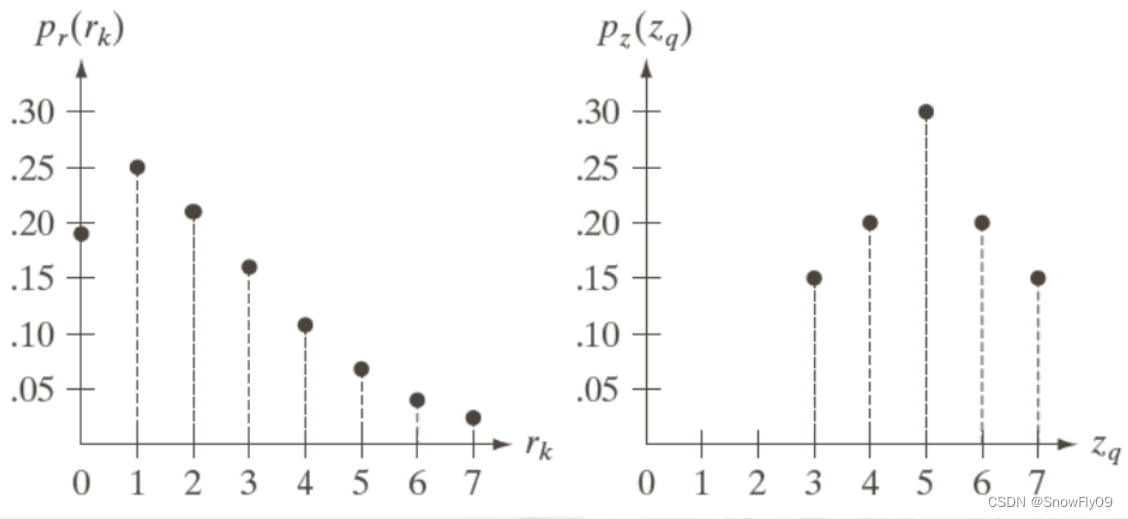
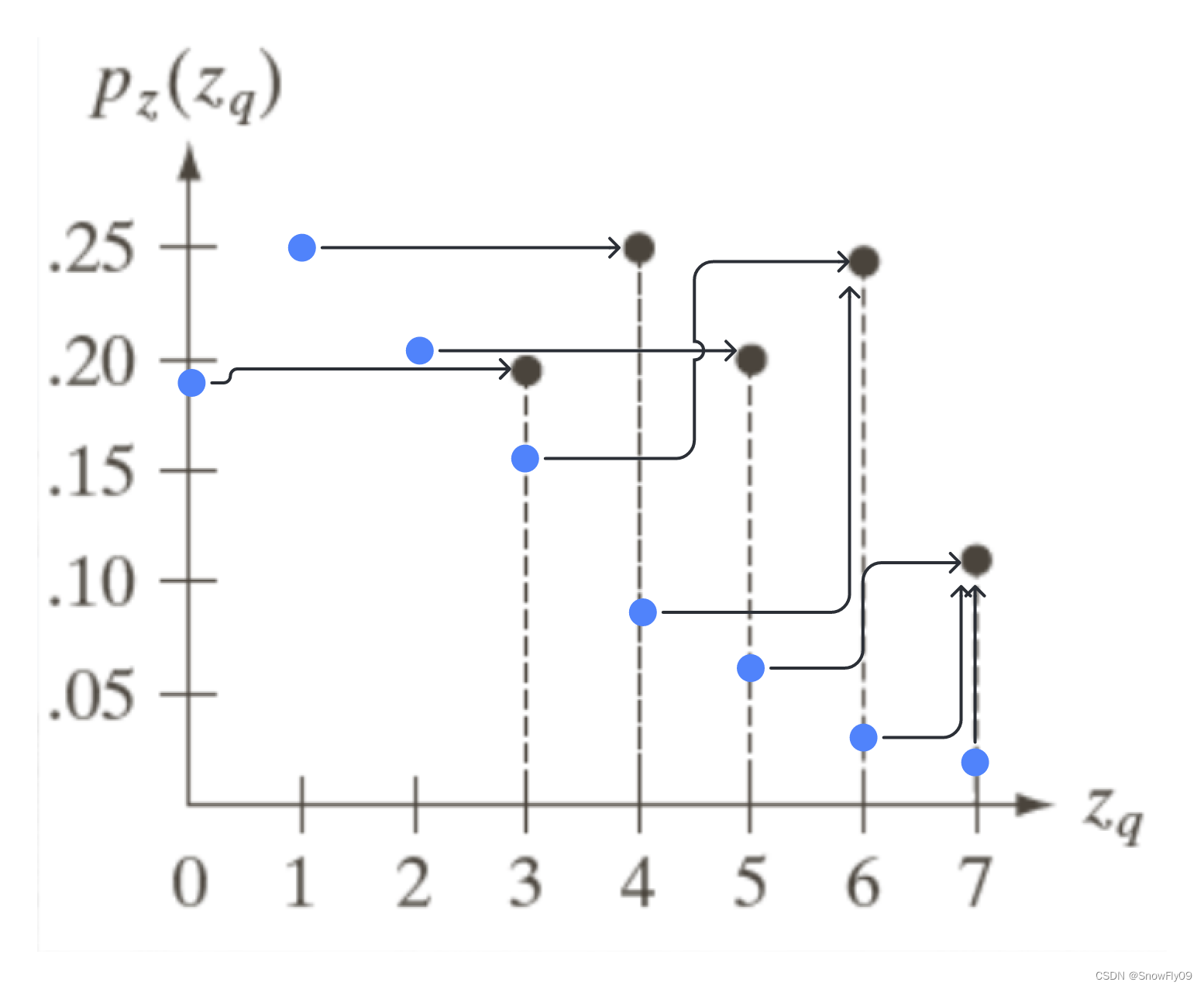
(1)對于原圖與參考圖均進行直方圖均衡:
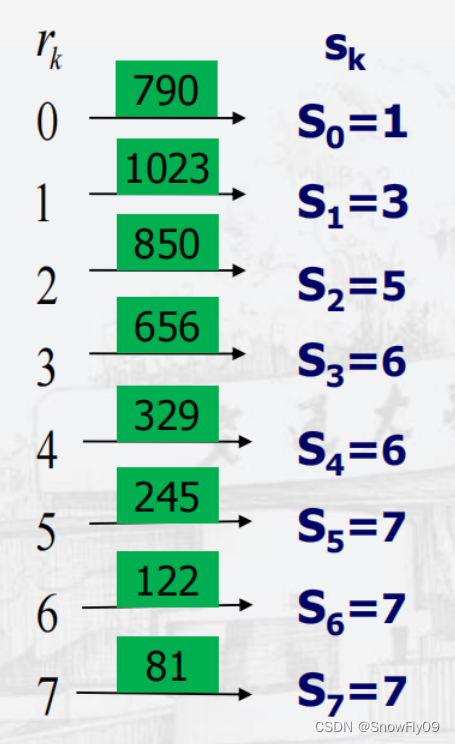
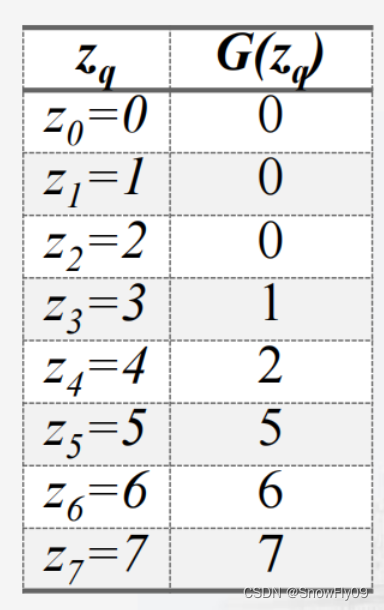
將s的值與G(z)的值相對應,每個s取最接近的G(z)值,當s離兩個G(z)值一樣接近時,取較小的那個,最終可以得到s對應z的映射,再加上原本r到s的映射,最終就能得到r到z的映射
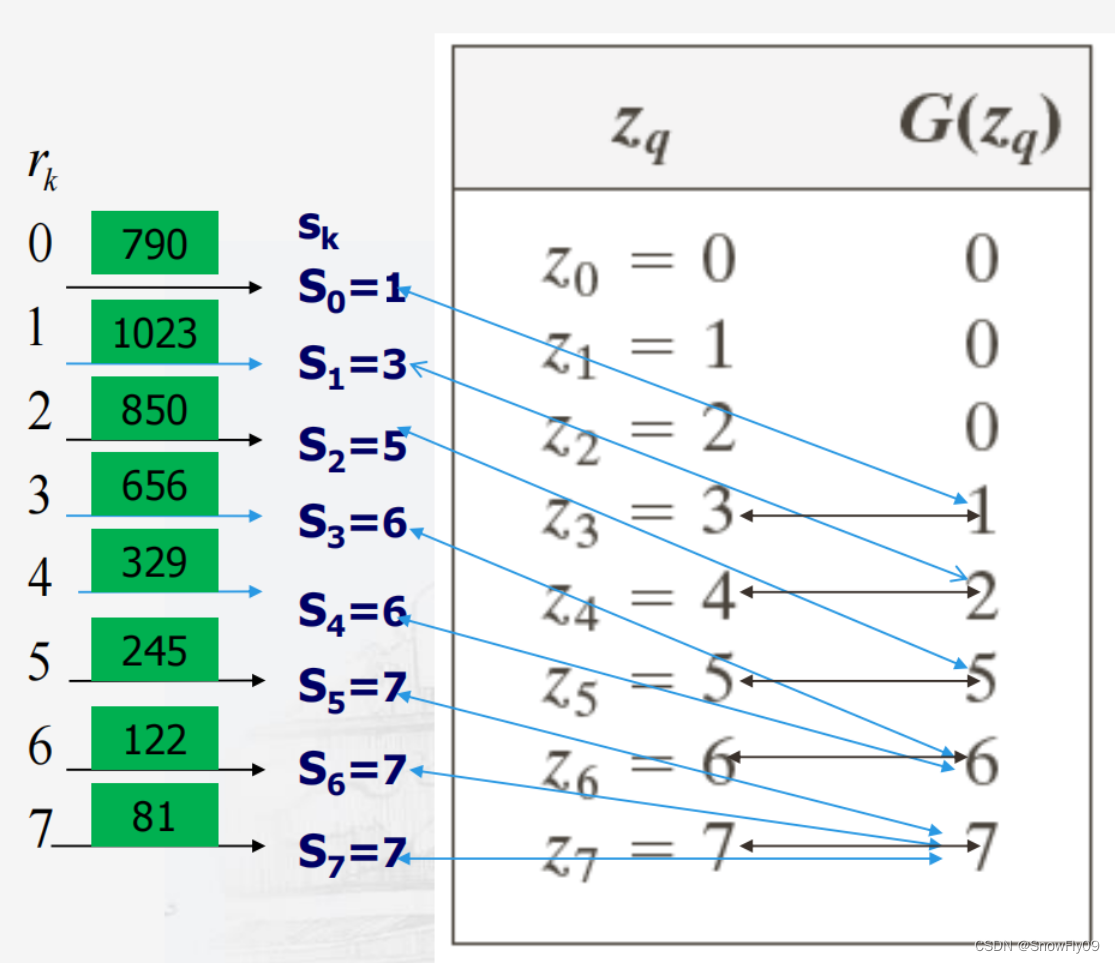
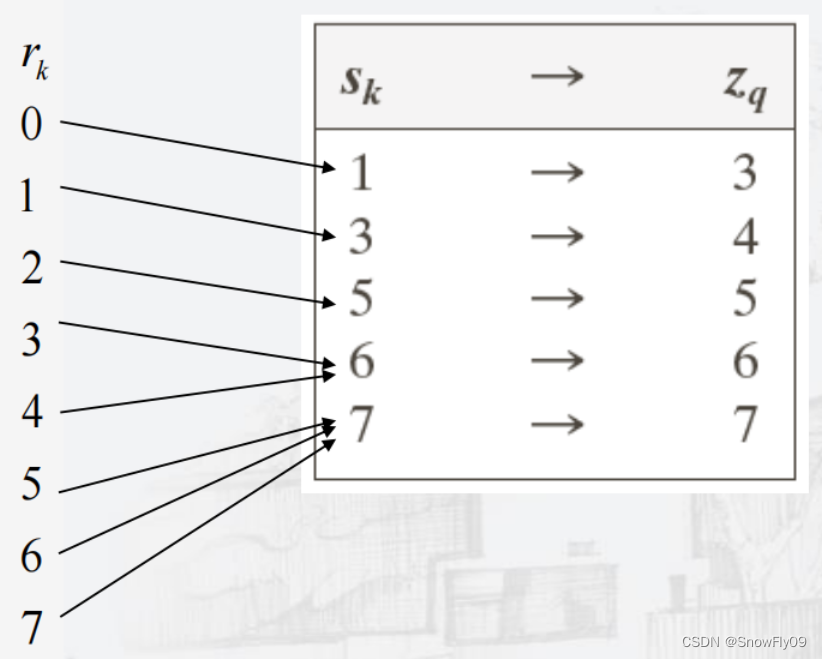
如此就可以得到目標的直方圖,需要注意的是,映射完后原圖的直方圖各灰度級概率密度并不與目標圖完全一致,而是指分布一致
空間濾波
濾波是指通過或拒絕一定范圍內的頻率分量,例如能夠通過低頻分量的濾波器叫做低通濾波器,最終效果可以對一幅圖片進行模糊處理。
根據執行的操作可以分為:線性空間濾波器和非線性空間濾波器去
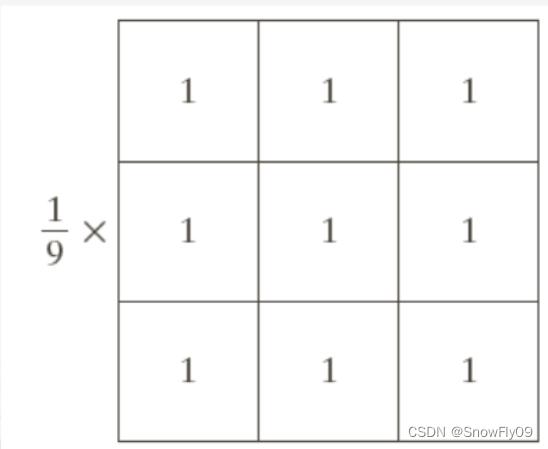
對于一個窗口為3x3的濾波器,其輸出為各位置上的系數與對應像素值的乘積之和
如果期望圖像中的像素變化為以該像素為中心的3x3鄰域的平均灰度,可以使用 R = 1 9 ∑ i = 1 9 z i R = \frac{1}{9}\sum\limits_{i=1}^9z_i R=91?i=1∑9?zi?
平滑空間濾波
平滑濾波用于模糊處理和降低噪聲
模糊處理經常用于預處理任務,可以去除圖像中的一些噪聲
平滑線性濾波器
可以歸入低通濾波器,主要作用是降低噪聲,去除圖像中的不相關細節,但也可能導致邊緣模糊或者由于灰度級數量不足導致的偽輪廓
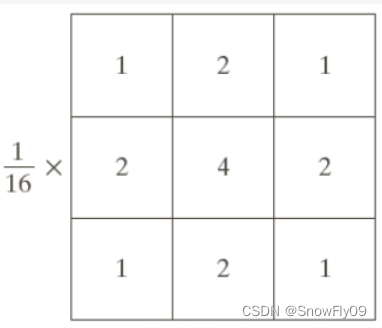
加權平均濾波:
非線性濾波器
統計排序濾波器是一種非線性濾波器,通過濾波器中包圍的圖像中所含像素的排序來決定中心像素的值
例如:中值濾波器,將濾波器內灰度的中值代替濾波器中心的值,此外除了取中值,還可以取最大值(最大值濾波器),最小值(最小值濾波器)
中值濾波器對于處理脈沖噪聲(椒鹽噪聲)非常有效
銳化空間濾波器
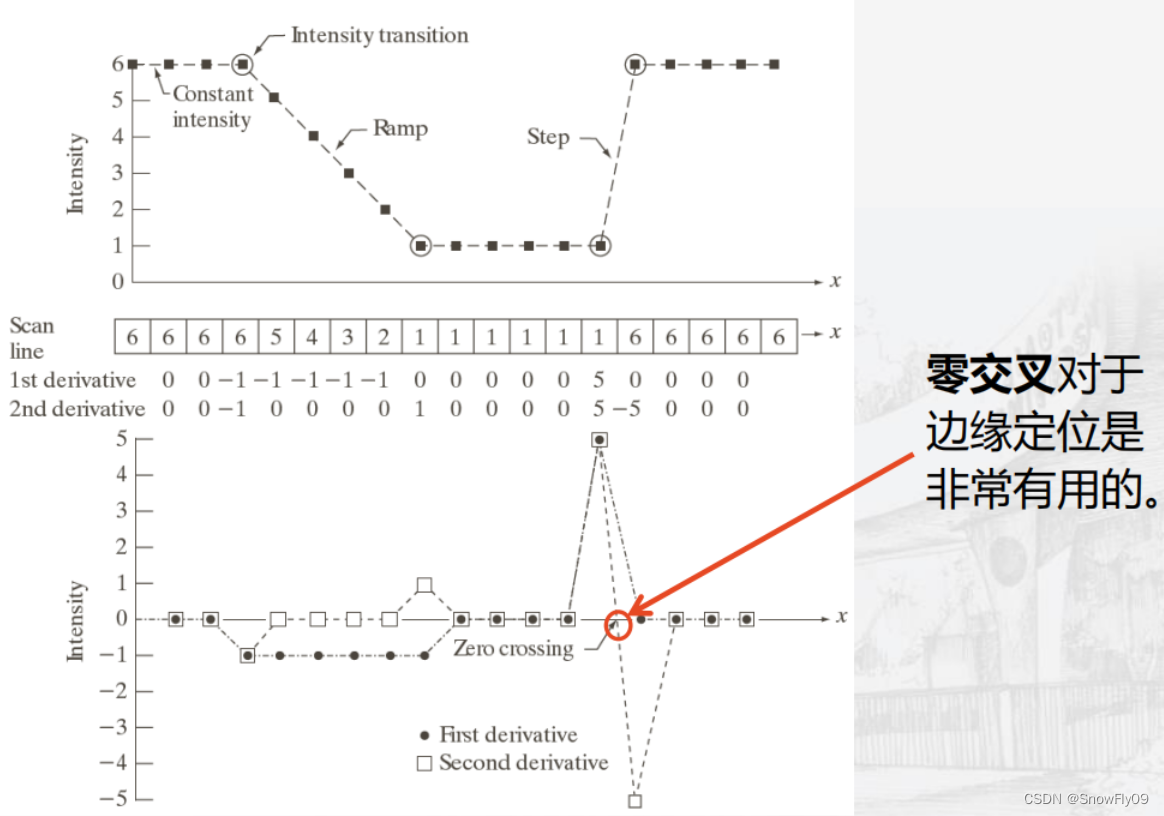
對于一階微分和二階微分的定義:
一階微分:(1)在恒定區域為0(2)在斜坡或臺階的起點處非0(3)在斜坡上非0
二階微分:(1)在恒定區域為0(2)在臺階或斜坡的起點處非0(3)在斜坡上為0
使用拉普拉斯算子進行圖像銳化
拉普拉斯算子是一種各向同性微分算子,這種濾波器的響應與其以何方向作用在圖像上無關。
對于兩個變量的拉普拉斯算子,
? 2 f = ? 2 f ? x 2 + ? 2 f ? y 2 \nabla^2f=\frac{\partial^2f}{\partial x^2}+\frac{\partial^2f}{\partial y^2} ?2f=?x2?2f?+?y2?2f?
將其以離散的形式表述,我們就可以得到:
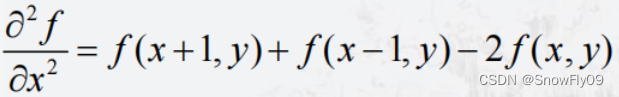
對于y也是同理:
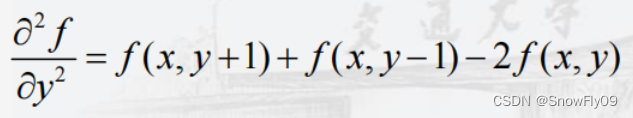
故最終可以得到:
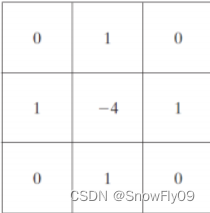
需要注意的是,拉普拉斯算子所產生的是一種濾波,可以認為是一種濾鏡,和原圖進行疊加才能起到相應的作用:

當拉普拉斯算子的中心常數為負時,c=-1,否則c=1



)





)

![[word] word怎樣轉換成pdf #職場發展#經驗分享#職場發展](http://pic.xiahunao.cn/[word] word怎樣轉換成pdf #職場發展#經驗分享#職場發展)

)



)

