前言
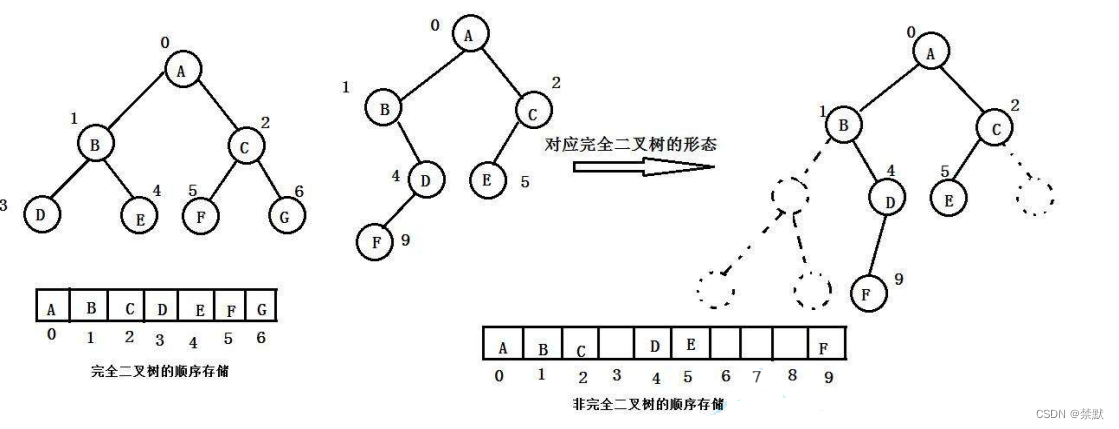
普通的二叉樹是不適合用數組來存儲的,因為可能會存在大量的空間浪費。而完全二叉樹更適合使用順序結 構存儲。現實中我們通常把堆 ( 一種二叉樹 ) 使用順序結構的數組來存儲,需要注意的是這里的堆和操作系統 虛擬進程地址空間中的堆是兩回事,一個是數據結構,一個是操作系統中管理內存的一塊區域分段。
1.堆的概念及結構
如果有一個關鍵碼的集合 K = { k0, k1,k2,…,k(n-1)},把它的所有元素按完全二叉樹的順序存儲方式存儲 在一個一維數組中,并滿足:Ki?<=K(2*i+1)且Ki<=K(2*i+2)(Ki?>=K(2*i+1)且Ki>=K(2*i+2) ?i =0 , 1 , 2…,則稱為小堆 (或大堆) 。將根結點最大的堆叫做最大堆或大根堆,根結點最小的堆叫做最小堆或小根堆。(這里的數字都是對應的下標)

堆的性質:
堆中某個結點的值總是不大于或不小于其父結點的值;
堆總是一棵完全二叉樹。
2.堆的創建和功能實現
2.1堆的基本結構的創建和相關函數聲明。
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>typedef int Datatype;
typedef struct Heap {Datatype* a;int size;int capacity;
}HP;
// 堆的初始化
void HeapInit(HP* hp);
// 堆的銷毀
void HeapDestory(HP* hp);
// 堆的插入
void HeapPush(HP* hp, Datatype x);
// 堆的刪除
void HeapPop(HP* hp);
// 取堆頂的數據
Datatype HeapTop(HP* hp);
// 堆的數據個數
bool HeapSize(HP* hp);
// 堆的判空
int HeapEmpty(HP* hp);
//向上調整
void Adjustup(Datatype* a, int child);
//向下調整
void Adjustdown(Datatype* a, int n, int parent);
//數據交換
void Swap(Datatype* p1, Datatype* p2);2.2 各函數的實現與講解
2.1堆的初始化和銷毀
堆的初始化和銷毀與以前的動態數組實現順序表和棧的初始化和銷毀基本是一樣的,在這里小編就不多解釋了。
// 堆的初始化
void HeapInit(HP* hp) {assert(hp);hp->a = NULL;hp->size = hp->capacity = 0;
}
// 堆的銷毀
void HeapDestory(HP* hp) {assert(hp);free(hp->a);hp->a = NULL;hp->size = hp->capacity = 0;
}2.2堆數據的插入
補充向上調整法
隨便給出一個數組,這個數組邏輯上可以看做一顆完全二叉樹,但是還不是一個堆,現在我們通過算法,把它構建成一個堆。根結點左右子樹不是堆,我們怎么調整呢?
向上調整法。
通過比較新插入元素與其父節點的值來判斷是否需要進行交換。如果新插入元素的值大于父節點的值,就將它們進行交換,并更新索引值。這樣,逐步向上調整,直到新插入元素找到了合適的位置,保證了堆的性質。
//向上調整
void Adjustup(Datatype* a,int child) {int parent = (child - 1) / 2;while (child > 0) {if (a[child] > a[parent]) {Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}elsebreak;}
}這個是建立大堆的向上調整,建立小堆的話直接改成小于
每插入一個元素,調用一次向上調整函數。
// 堆的插入
void HeapPush(HP* hp, Datatype x) {assert(hp);if (hp->size == hp->capacity) {int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;Datatype* temp = (Datatype*)realloc(hp->a, sizeof(Datatype) * newcapacity);if (temp == NULL) {perror("realloc fail");return;}hp->a = temp;hp->capacity = newcapacity;}hp->a[hp->size] = x;hp->size++;Adjustup(hp->a, hp->size-1);
}例如數組a[]={1, 5, 3, 8, 7, 6},依次插入并建立大堆后的順序是:
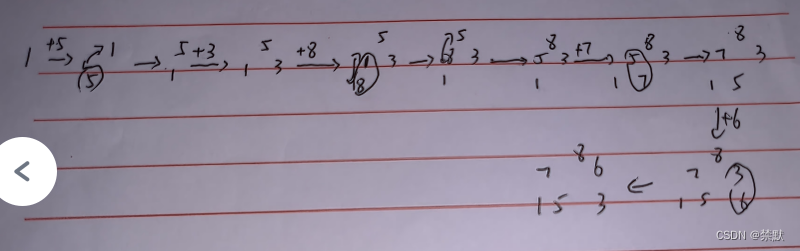
- 插入 1,堆變為 [1]
- 插入 5,堆變為 [5, 1]
- 插入 3,堆變為 [5, 1, 3]
- 插入 8,堆變為 [8, 5, 3, 1]
- 插入 7,堆變為 [8, 7, 3, 1, 5]
- 插入 6,堆變為 [8, 7, 6, 1, 5, 3]
所以,建立大堆后的順序是 [8, 7, 6, 1, 5, 3]。
2.3堆的刪除
補充向下調整法
在這里慣性思維是直接刪除頭頂數據,然后重新建堆,通過向上調整法,但是我們需要從最后一個元素依次遍歷向上調整。
這里我們采用向下調整法。
刪除堆是刪除堆頂的數據,將堆頂的數據根最后一個數據一換,然后刪除數組最后一個數據,再進行向下調整算法。
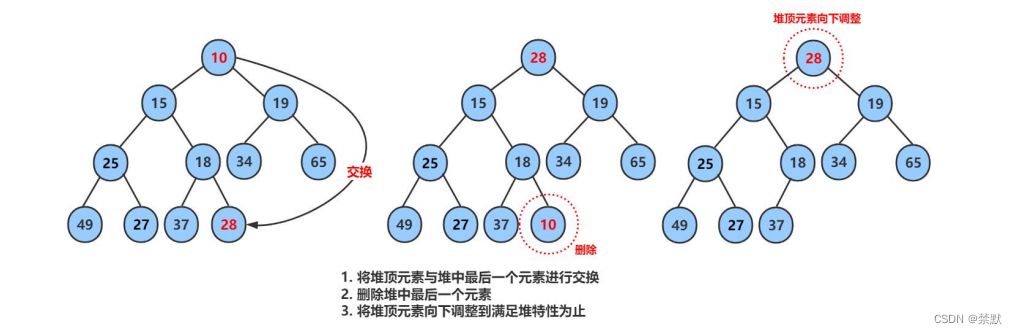
本張圖是小堆的刪除。大堆的刪除方式是一樣的。
因為堆數據插入是建立大堆的,所以這里的代碼是大堆的向下調整。
//向下調整
void Adjustdown(Datatype* a, int n, int parent) {//假設法,假設左孩子大int child = parent * 2 + 1;while (child < n ) {if (child + 1 < n && a[child + 1] > a[child])//a[child+1]<a[child]child = child + 1;if (a[child] > a[parent]) { //a[child]<a[parent]Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else break;}
}堆的刪除
// 堆的刪除
void HeapPop(HP* hp) {assert(hp);assert(hp->size > 0);Swap(&hp->a[0], &hp->a[hp->size - 1]);hp->size--;Adjustdown(hp->a, hp->size, 0);
}最后我們會發現刪除的數據是從大到小排列的,這里就可以牽扯到堆排序的應用,小編在下節會講解的。
2.4其他函數實現(交換,判空,堆頂數據,數據個數)
//數據交換
void Swap(Datatype* p1, Datatype* p2) {Datatype temp = *p1;*p1 = *p2;*p2 = temp;
}
// 取堆頂的數據
Datatype HeapTop(HP* hp) {assert(hp);assert(hp->size > 0);return hp->a[0];
}
// 堆的數據個數
int HeapSize(HP* hp) {assert(hp);return hp->size;
}
// 堆的判空
bool HeapEmpty(HP* hp) {assert(hp);return hp->size == 0;}3.代碼測試
#include "Heap.h"
void TestHeap1()
{int a[] = { 4,2,8,1,5,6,9,3,2,23,55,232,66,222,33,7,66,3333,999 };//int a[] = { 1,5,3,8,7,6 };HP hp;HeapInit(&hp);for (int i = 0; i < sizeof(a) / sizeof(int); i++){HeapPush(&hp, a[i]);}printf("堆的大小為%d\n", HeapSize(&hp));int i = 0;while (!HeapEmpty(&hp)){printf("%d ", HeapTop(&hp));//a[i++] = HPTop(&hp);HeapPop(&hp);}printf("\n");
}
/*// 找出最大的前k個int k = 0;scanf("%d", &k);while (k--){printf("%d ", HeapTop(&hp));HeapPop(&hp);}printf("\n");HeapDestory(&hp);
}*/
int main(){
TestHeap1();
return 0;
}4.堆的選擇題(方便大家理解)
1. 下列關鍵字序列為堆的是:(A)A 100 , 60 , 70 , 50 , 32 , 65? ? ? ? ? ?? B 60 , 70 , 65 , 50 , 32 , 100? ? ? ? ? ?? C 65 , 100 , 70 , 32 , 50 , 60D 70 , 65 , 100 , 32 , 50 , 60? ? ? ? ? ?? E 32 , 50 , 100 , 70 , 65 , 60? ? ? ? ? ?? F 50 , 100 , 70 , 65 , 60 , 322. 已知小根堆為 8 , 15 , 10 , 21 , 34 , 16 , 12 ,刪除關鍵字 8 之后需重建堆,在此過程中,關鍵字之間的比較次數是(C)。A 1? ? ? ? ? ? ? ? ? ? ? B 2? ? ? ? ? ? ? ? ? ? ? ? C 3? ? ? ? ? ? ? ? ? ? ? ? D 43. 最小堆 [ 0 , 3 , 2 , 5 , 7 , 4 , 6 , 8 ], 在刪除堆頂元素 0 之后,其結果是(C)A [ 3 , 2 , 5 , 7 , 4 , 6 , 8 ]? ? ? ? ? ? ? ? ? B [ 2 , 3 , 5 , 7 , 4 , 6 , 8 ]C [ 2 , 3 , 4 , 5 , 7 , 8 , 6 ]? ? ? ? ? ? ? ? ? D [ 2 , 3 , 4 , 5 , 6 , 7 , 8 ]





)

![[word] word怎樣轉換成pdf #職場發展#經驗分享#職場發展](http://pic.xiahunao.cn/[word] word怎樣轉換成pdf #職場發展#經驗分享#職場發展)

)



)





