#用matlab解決施密特正交規范化矩陣之后，我又想到矩陣的微分方程計算量真的太大了，來回轉化讓我頭大，于是我嘗試了一下用matlab建立模型來解決這類問題。
代碼部分如下：注解還挺清晰的：
%%%解微分方程組%eg：x1t'=3*x1t+x2t% x2t'=x1t+2*x2t+x3t% x3t'=x2t+3*x3t%1.首先設出xtsyms x1t;syms x2t; syms x3t;syms x1t_;syms x2t_; syms x3t_;xt1=[x1t;x2t;x3t];xt_1=[x1t_;x2t_;x3t_];%用_代表一撇（導數）%正常帶入進去%我們有：xt_=[x1t_;x2t_;x3t_]% =[3*x1t+x2t;x1t+2*x2t+x3t;x2t+3*x3t]% =[3 1 0;1 2 1;0 1 3]*[x1t;x2t;x3t]% =[3 1 0;1 2 1;0 1 3]*xtA=[3 1 0;1 2 1;0 1 3];%2.對A進行對角化%2.1求A的特征值syms t;%法1：因式分解f=t*A-eye(3);%是多少寫多少fa=det(f);%求行列式fac=factor(fa);%法2：直接求解[v,D]=eig(A);%v為特征向量，D為特征值disp('特征值：');disp(diag(D)');disp('特征向量：');disp(v);%我們可知：p-1*A*p=D;% 有A=p*D*p-1%我們接著帶入得：xt'=P*D*P-1*xt；%移項湊形式： p-1*xt'=D*p-1*xt；%引入變量 Yt=p-1*xt=[y1t；y2t；y3t]%有 yt'=D*yt%可得：[y1t';y2t';y3t']=D*[y1t;y2t;y3t]=[y1t;3*y2t;4*y3t];syms y1t;syms y2t;syms y3t;syms y1t_;syms y2t_;syms y3t_;yt1=[y1t;y2t;y3t];y1t_1=[y1t_;y2t_;y3t_];%截圖：%微積分知識求解微分方程%代入方程得到：[y1t,y2t,y3t]=dsolve('Dy1t=y1t','Dy2t=3*y2t','Dy3t=4*y3t','t');yt=[y1t;y2t;y3t];%又知：xt=p*ytxt=v*yt;disp(xt);
%即為我們得到的答案我們帶入例題驗證一下結論：
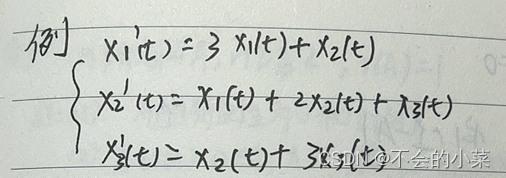
我們直接帶入我們的代碼：
得到：
結果是正確的，遇到類似題目可以直接帶入模型進行求解，大大節約了我們的時間！
謝謝大家的支持啦~
)
