第二章









































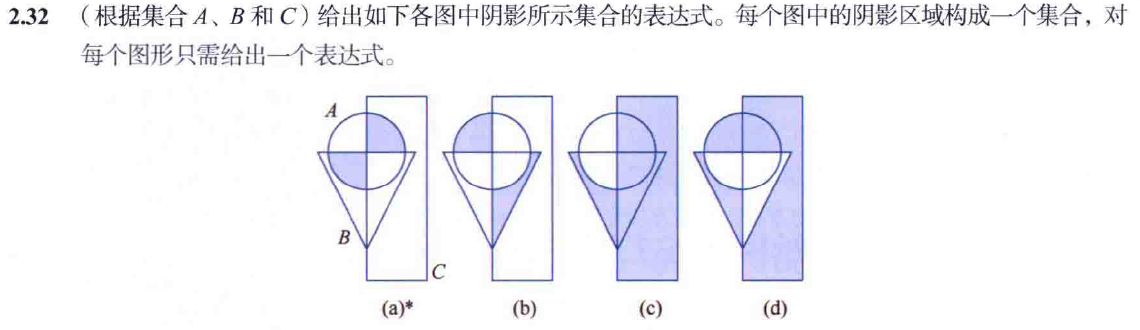














第三章







 .
.

















































第四章







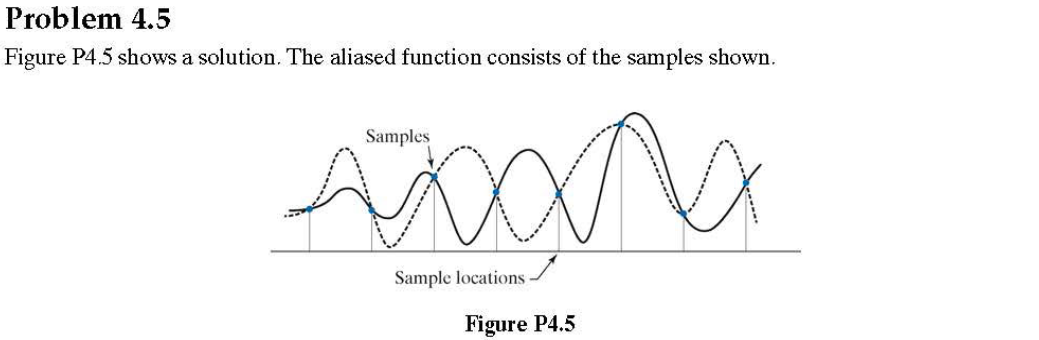

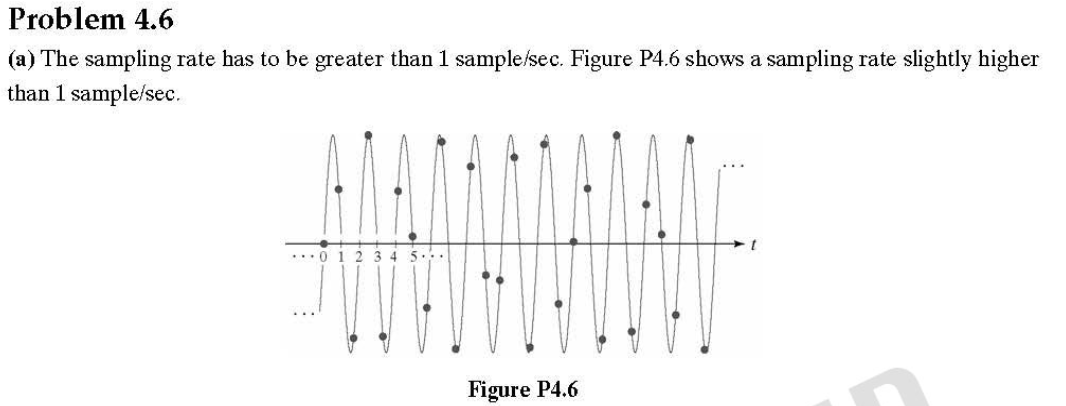











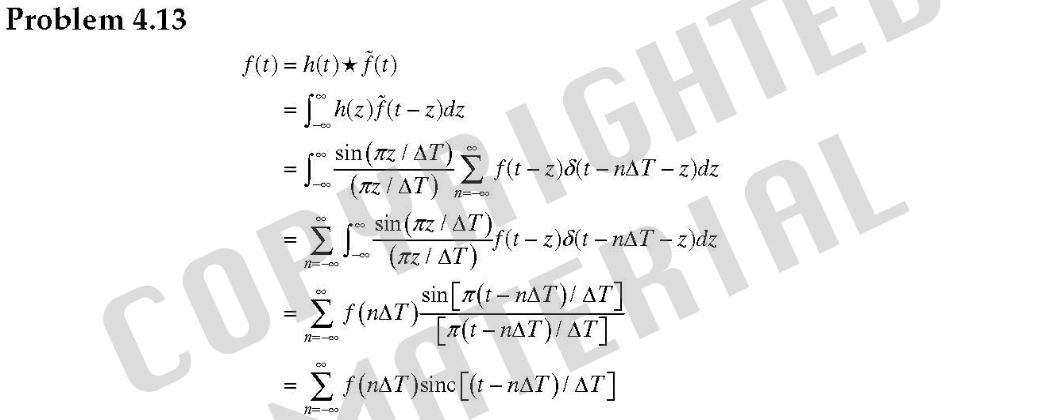







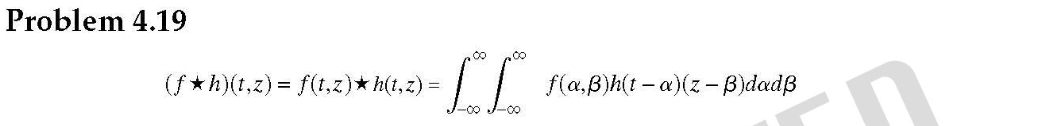















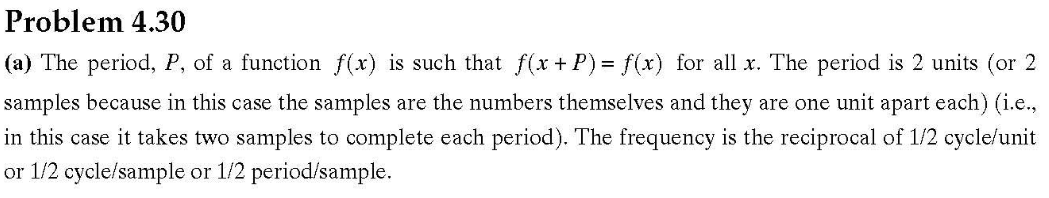



















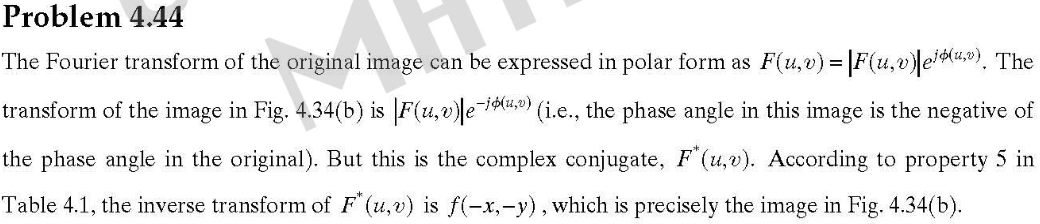











傅里葉變換是一個線性過程,而計算梯度的平方根和平方根則是非線性運算。傅里葉變換可以用來計算微分的差值(如問題4.50),但必須在空間域中直接計算平方和平方根值。



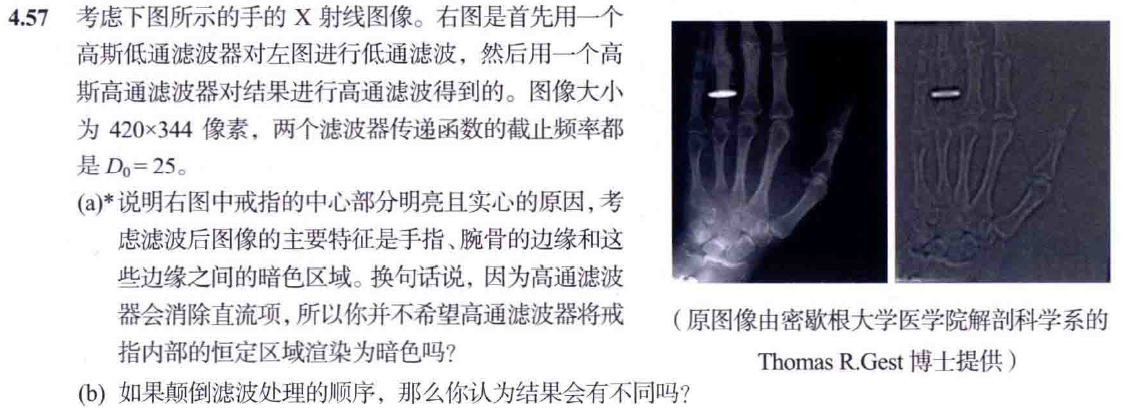
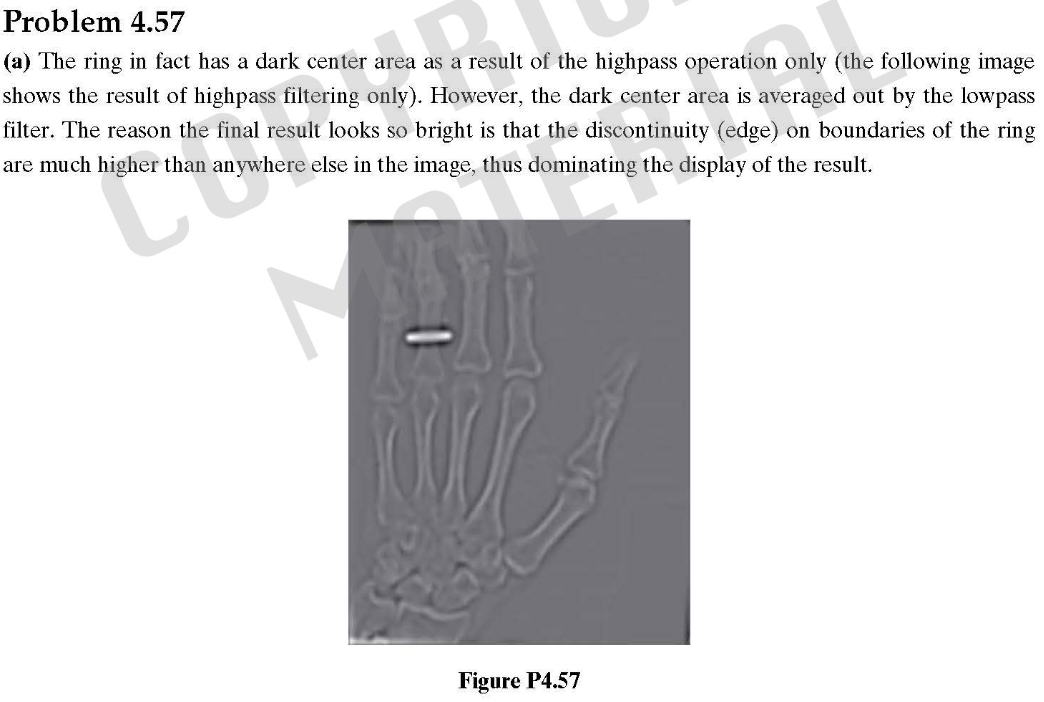
(a)實際上,由于高通操作,環有一個暗中心區域(以下圖像僅顯示高通濾波的結果),而暗中心區域由低通濾波器平均。最終結果看起來如此明亮的原因是,環形邊界上的不連續性(邊緣)比圖像中的任何地方都要高得多,從而控制了結果的顯示。




第五章



















(a) 圖為正弦波完整周期的整數。
(b) 位于 u 0 u_0 u0?和 ? u 0 -u_0 ?u0?處的一對純共軛脈沖。


























解決方案如圖5.41所示。要了解為什么包含中心單點的圖像的 Radon 變換是一條直線請參閱圖 5.36、5.37 和方程 (5-101),這個方程告訴我們這個方程告訴我們,對于每個角度 θ,我們通過改變 ρ 來計算 Radon 變換,以找到沿線 L ( θ , ρ ) L(θ,ρ) L(θ,ρ) 在圖像上的總和。但是,對于給定的圖像和任意角度 θ,唯一包含單個點的線是 ρ = 2 M / 2 ρ=\sqrt{2}M/2 ρ=2?M/2(該點位于正方形圖像對角線的一半)的線。此外,θ 的任何值的總和將等于點的強度。因此,Radon變換將是位于 ρ = 2 M / 2 ρ=\sqrt{2}M/2 ρ=2?M/2 處的恒定強度直線的圖像,如圖所示。










第六章



使用根據三個對象顏色的波長進行調諧的濾色器。使用特定濾波器后,只有顏色與該波長相對應的物體才會在單色相機上產生顯著響應。電動濾波器轉輪可用于通過計算機控制濾波器位置。如果其中一種顏色是白色,那么三個濾波器的響應將大致相等且高。如果其中一種顏色是黑色,則三個濾波器的響應將大致相等且較低。
















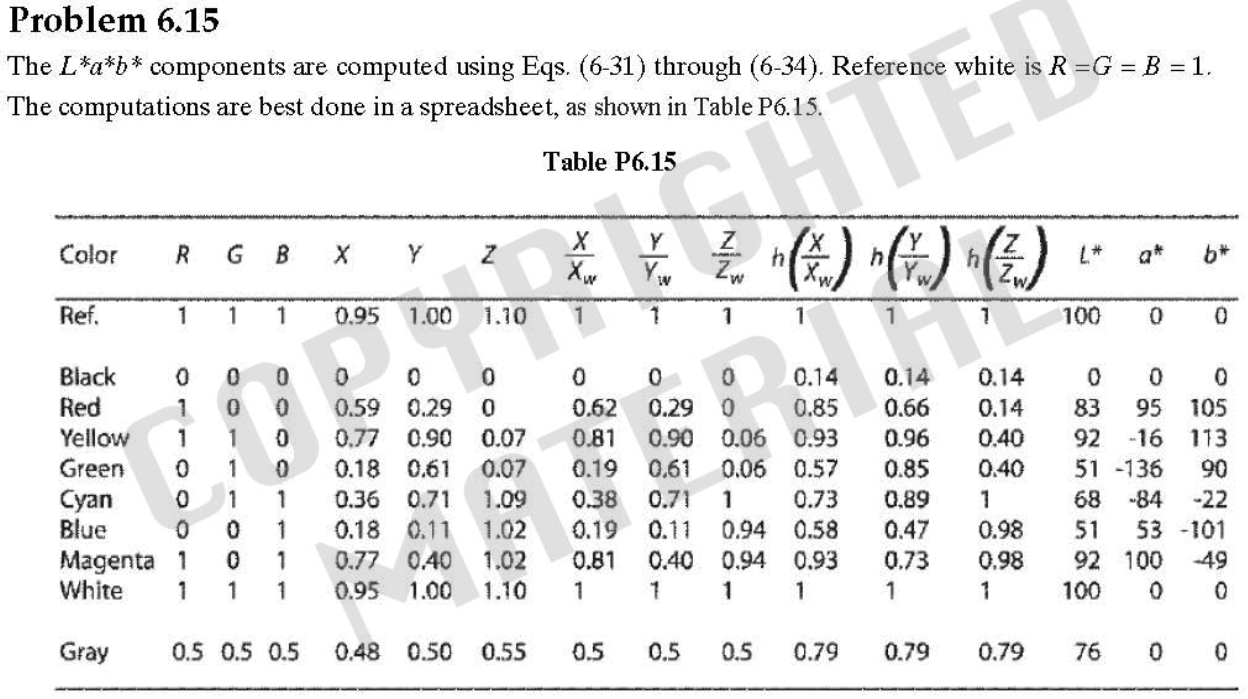
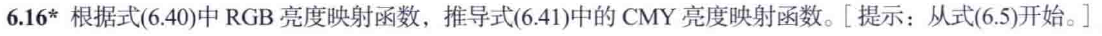












飽和度圖像是恒定的,因此平滑它將產生相同的常數值。


第七章
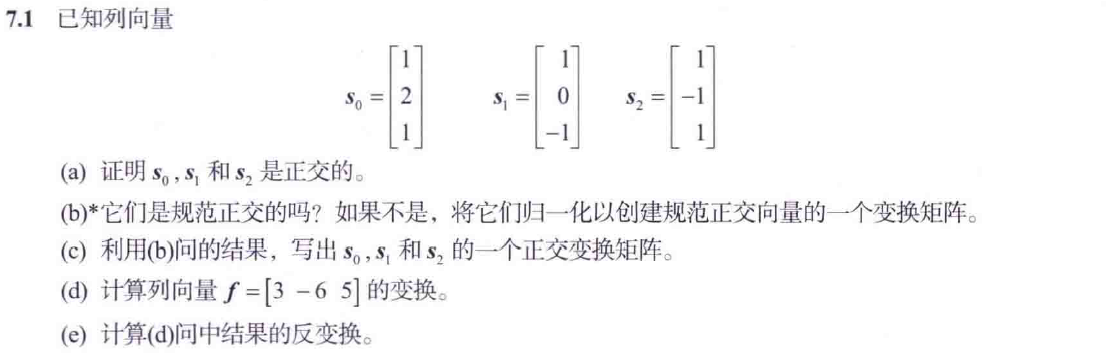




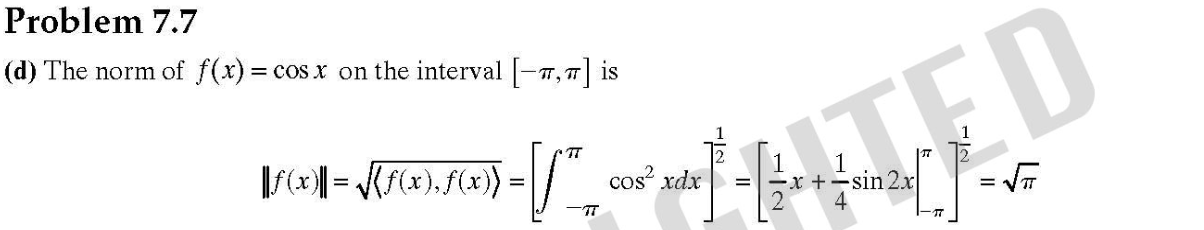










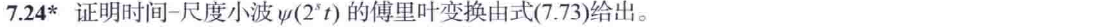






7.40沒有





第八章













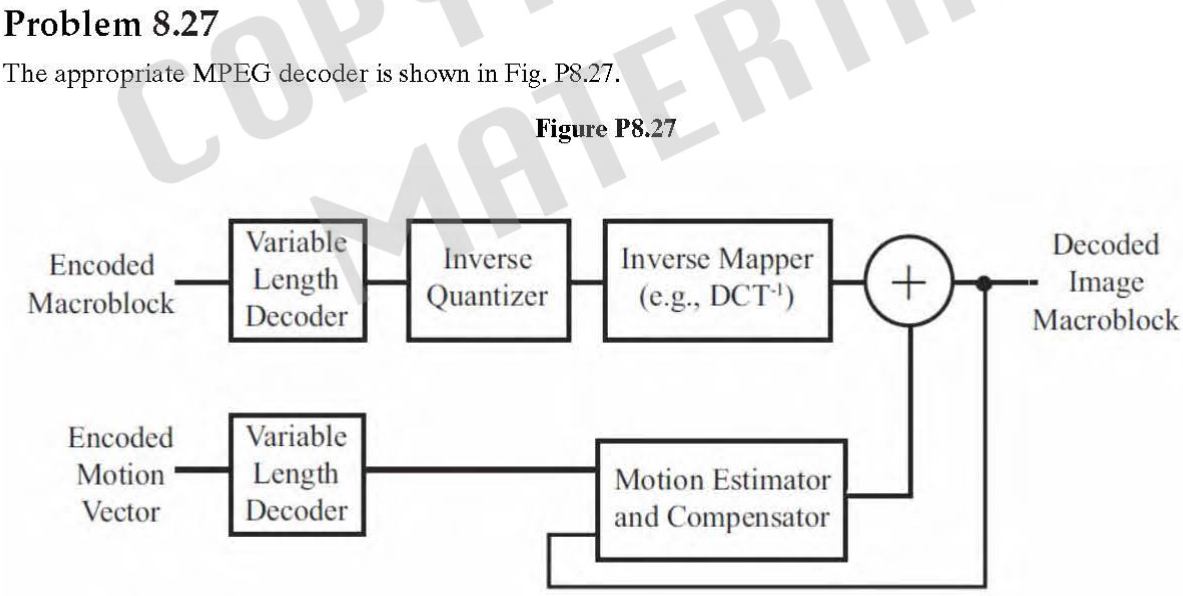




第九章
















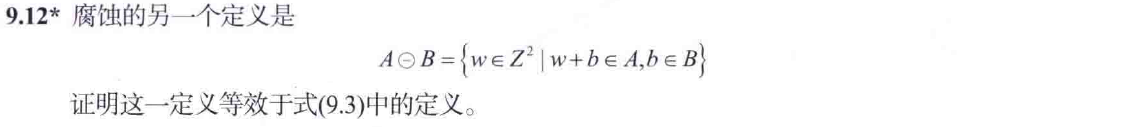


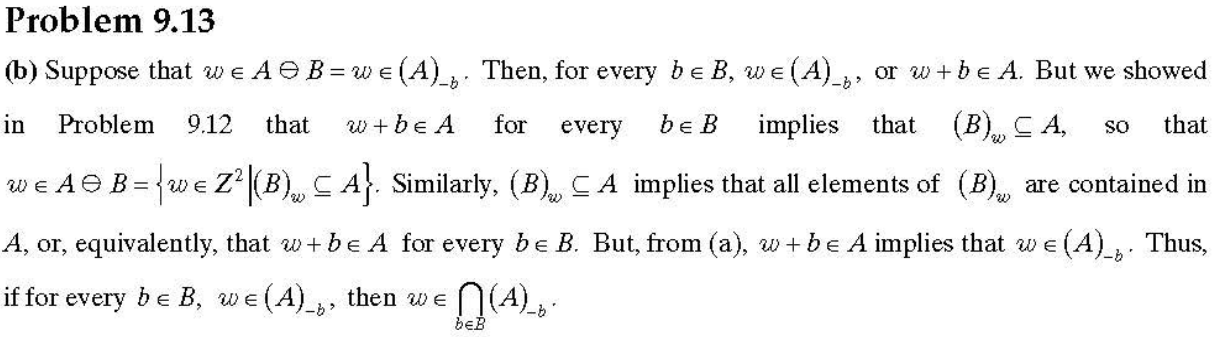
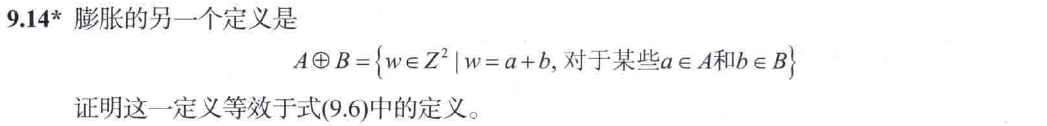
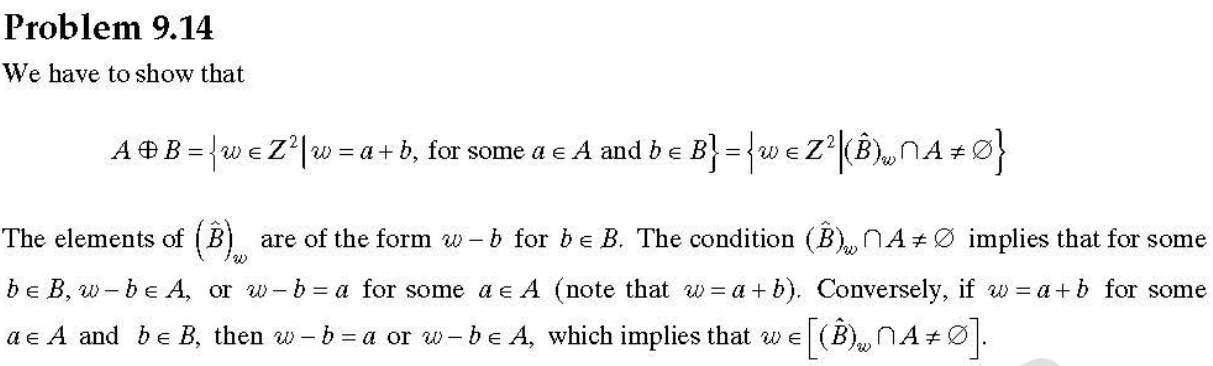
















A4-連通曲線不能有對角線連接,因此算法只需檢查輸入圖像中的對角線項,從3×3鄰域的中心點到曲線的下一個點。對于所發現的這些像素,在中心像素的左側(或右側)添加一個1,同時考慮到從中心像素到下一個像素的移動方向。然后,鑒于這條曲線只有一個像素寬,沒有分支,我們只需要檢查下圖第一行的可能性(以所示方式標記鄰域的原因很快就會清楚):
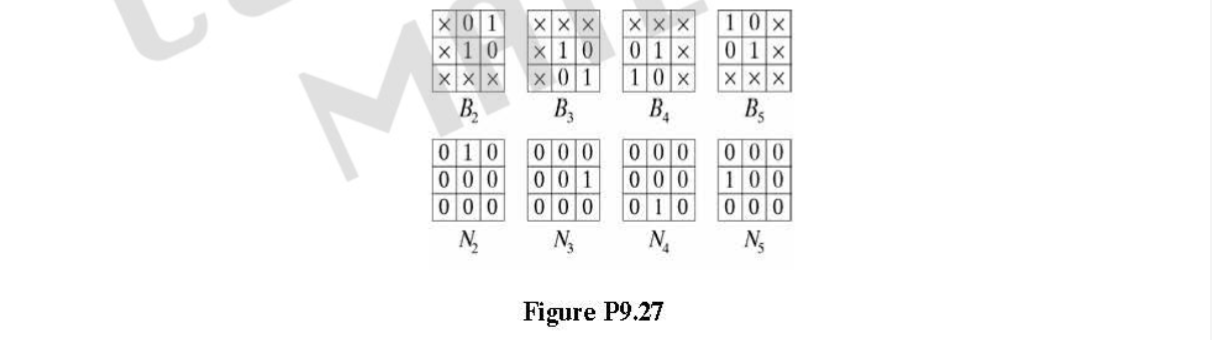
圖P9.27第一行中顯示的結構元素考慮到了這樣一個事實,即我們只需要在行進方向上查看每個像素前面的一個像素,并確保訪問到所有點。因為我們只看前面的一個像素,所以我們必須保證對角線每邊的像素是 0;其他的無關緊要,因此不關心條件。
該算法由以下幾個主要階段組成。
1)使用問題圖第一行中的每個結構元,將擊中-擊不中變換應用于包含曲線的圖像,一次應用一個。用 2 標記 B 2 B_2 B2? 找到的命中,用 3 標記 B 3 B_3 B3? 找到的命中,依此類推。
2)對于標記為2的每一個點,在圖P9.27的第二行,用 N 2 N_2 N2?執行其3×3鄰域的邏輯OR運算(這會在將對角線連接轉換為 4 連接所需的位置添加一個 1),對其他3種類型的命中重復上述步驟。

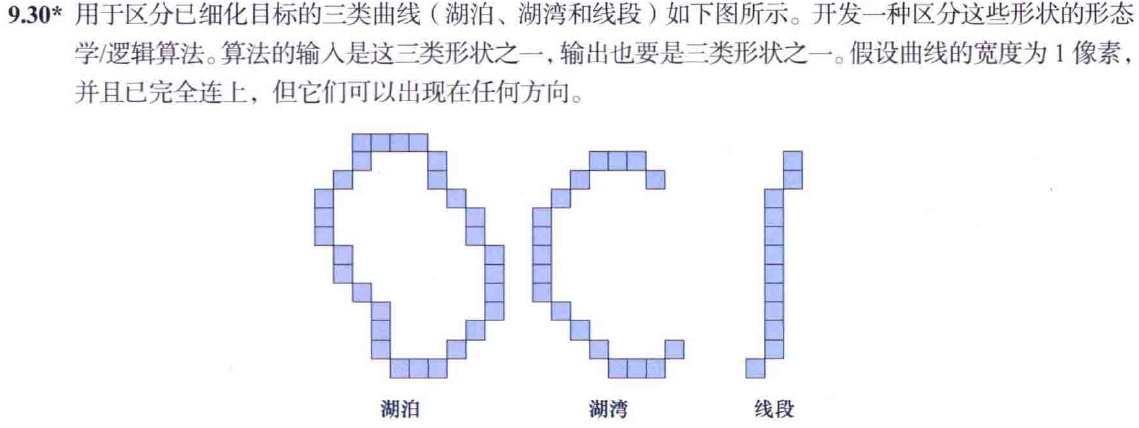
湖泊與其他兩個特征之間的主要區別在于前者形成一個封閉的輪廓。假設一次處理一個形狀,則區分三個形狀的基本兩步法如下:
步驟 1。將端點檢測器應用于對象。如果未找到端點,則對象是湖,否則就是海灣或線。
步驟 2。有很多方法來區分海灣和直線。最簡單的方法之一是確定一條連接對象的兩個端點的線,如果對象與這條線只有端點處的兩個交點,那么這個圖形就是海灣,否則它就是一條直線。在一些反常情況下,這種檢測會失效,并且需要在這個過程中建立額外的“信息”,但隨著細化圖形分辨率的增加,這些反常情況的可能性會降低。































(a) Color the image border pixels the same color as the particles (white). Call the resulting set of border pixels β. Apply the connected component algorithm (Section 9.6). All connected components that contain elements from β are particles that have merged with the border of the image.
(a)將圖像邊框像素著色為與顆粒相同的顏色(白色)。調用生成的邊框像素集 β。應用連接組件算法(第 9.6 節)。包含來自 β 的元素的所有連接成分都是與圖像邊框接觸的顆粒。

第十章




























(b)直接實現二維空間卷積需要在 f ( x , y ) f(x,y) f(x,y)的每個位置進行 n 2 次 n^2次 n2次乘法,因此乘法的總數為 n 2 × M × N n^2×M×N n2×M×N。另一方面,在圖像中每一行的每個位置,一維卷積都需要 n n n次乘法,對于所有行的傳遞,總共需要 n × M × N n×M×N n×M×N次乘法。然后,所有列的傳遞都需要 n × M × N n×M×N n×M×N次,總共有 2 n M N 2nMN 2nMN次乘法。計算優勢 A A A是

這與圖像大小無關。例如,如果 n = 25 , A = 12.5 n= 25,A=12.5 n=25,A=12.5,那么直接實現二維卷積所需的乘法次數是實現一維卷積的 12.5 12.5 12.5 倍。這與方程(3-44)當 m = n m=n m=n時一致。當然,乘法的數量本身很大程度上取決于圖像大小。




















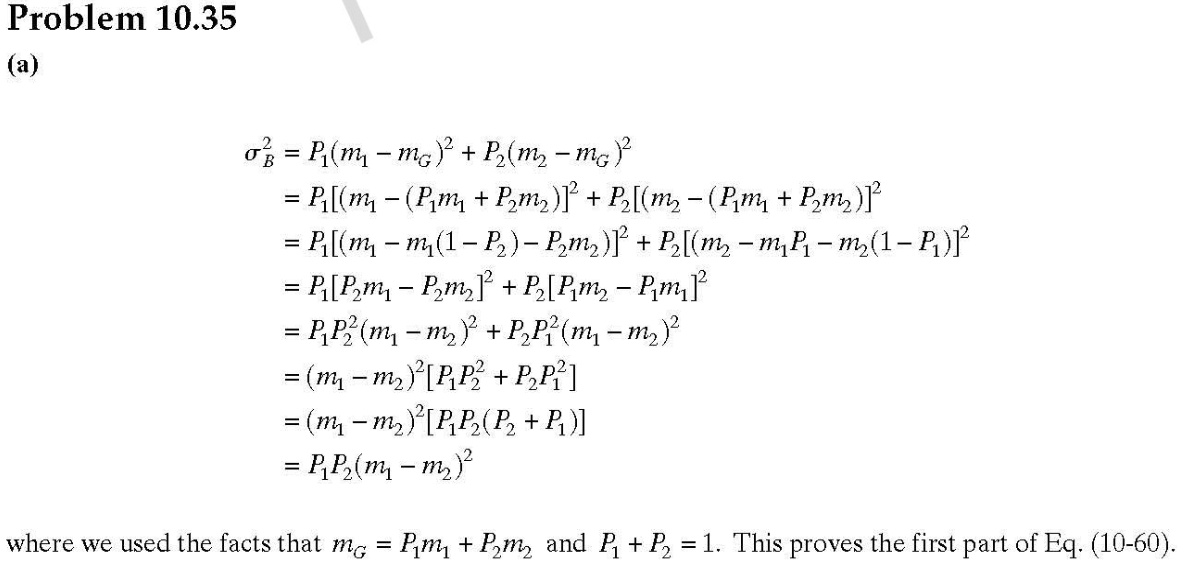



(a)設 R 1 R_1 R1?和 R 2 R_2 R2?,分別表示像素強度大于 T T T和小于或等于 T T T的區域,閾值 T T T是強度值,由變換函數映射到值 T ′ = 1 ? T T'=1-T T′=1?T。 R 1 R_1 R1?中的值被映射到 R 1 ′ R_1' R1′?, R 2 R_2 R2?中的值被映射到 R 2 ′ R_2' R2′?。重要的是, R ′ R' R′中的所有值都在 T ′ T' T′下,且 R 2 ′ R_2' R2′?中的所有值都等于或大于 T ′ T' T′。不等式的意義已被逆轉,但這兩個區域的強度的可分性得到了保持。






【沒寫圖割】










(a) 給定水平方向上 10% 的圖像區域被 2.5 厘米長的子彈占據。由于成像設備是方形的(256 × 256 個像素),因此假設沒有光學畸變,相機會觀察 25 厘米×25 厘米的區域。因此,像素之間的距離為 25 / 256 = 0.098 25/256 =0.098 25/256=0.098 厘米/像素。子彈的最大速度為 1000 1000 1000 米/秒 = 100 , 000 100,000 100,000 厘米/秒。在這個速度下,子彈將行進 100 , 000 / 0.98 = 1.02 × 1 0 6 100,000/0.98 = 1.02× 10^6 100,000/0.98=1.02×106像素/秒。要求子彈在曝光期間的行進不超過一個像素。即 ( 1.02 × 1 0 6 1.02×10^6 1.02×106 像素/秒)× K K K 秒 ≤ 1 ≤1 ≤1 像素。所以, K ≤ 9.8 × 1 0 ? 7 K ≤ 9.8×10^{-7} K≤9.8×10?7 秒。
? 在有反光物體的閃爍情況下,圖像往往會變暗,物體會發光。那么,第 10.8 節中討論的空間技術就足夠了。

第十一章































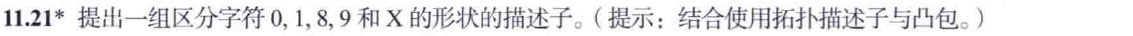























第十二章








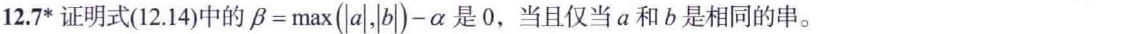




























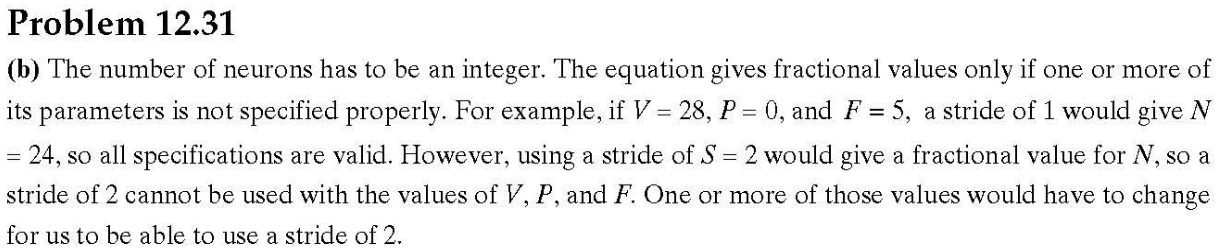

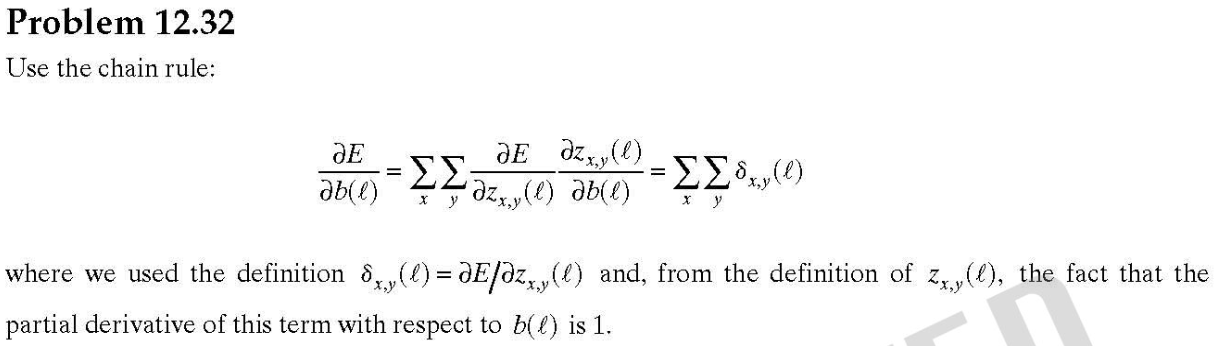

實現)
)
)
)

![[AI Google] 介紹 VideoFX,以及 ImageFX 和 MusicFX 的新功能](http://pic.xiahunao.cn/[AI Google] 介紹 VideoFX,以及 ImageFX 和 MusicFX 的新功能)




)






)
