前言：

? ? ? ? 這篇文章，我們就來了解一些鮮為人知的排序，桶排序和基數排序。

桶排序：

桶排序的思想：

????????桶排序的思想就是把待排序的數盡量均勻地放到各個桶中，再對各個桶進行局部的排序，最后再按序將各個桶中的數輸出，即可得到排好序的數。

????????桶排序（Bucket Sort）又稱箱排序，是一種比較常用的排序算法。其算法原理是將數組分到有限數量的桶里，再對每個桶分別排好序（可以是遞歸使用桶排序，也可以是使用其他排序算法將每個桶分別排好序），最后一次將每個桶中排好序的數輸出。

????????首先確定桶的個數。因為桶排序最好是將數據均勻地分散在各個桶中，那么桶的個數最好是應該根據數據的分散情況來確定。首先找出所有數據中的最大值max和最小值min；

求桶的個數：?

????????根據max和min確定每個桶所裝的數據的范圍 size，有size = (max - min) / n + 1，n為數據的個數，需要保證至少有一個桶，故而需要加個1；

求桶數據范圍差值：

????????求得了size即知道了每個桶所裝數據的范圍，還需要計算出所需的桶的個數count，有
count?= (max - min) / size + 1，需要保證每個桶至少要能裝1個數，故而需要加個1；

桶的數據范圍：

????????求得了size和cnt后，即可知第一個桶裝的數據范圍為 [min, min + size)，第二個桶為 [min + size, min + 2 * size)，…，以此類推。

????????因此步驟2中需要再掃描一遍數組，將待排序的各個數放進對應的桶中。

對桶中的元素進行排序：?

????????對各個桶中的數據進行排序，可以使用其他的排序算法排序，例如快速排序；也可以遞歸使用桶排序進行排序；

統一排序：

? ? ? ? 最后將各個桶中排好序的數據依次輸出，最后得到的數據即為最終有序。

圖解：

接下來舉一個例子：

例如，待排序的數為：3, 6, 9, 1

1）求得 max = 9，min = 1，n = 4
size = （9 - 1) / n + 1 = 3
count = (max - min) / size + 1 = 3

2）由上面的步驟可知，共3個桶，每個桶能放3個數，第一個桶數的范圍為 [1, 4)，第二個[4, 7)，第三個[7, 10)
掃描一遍待排序的數，將各個數放到其對應的桶中，放完后如下圖所示：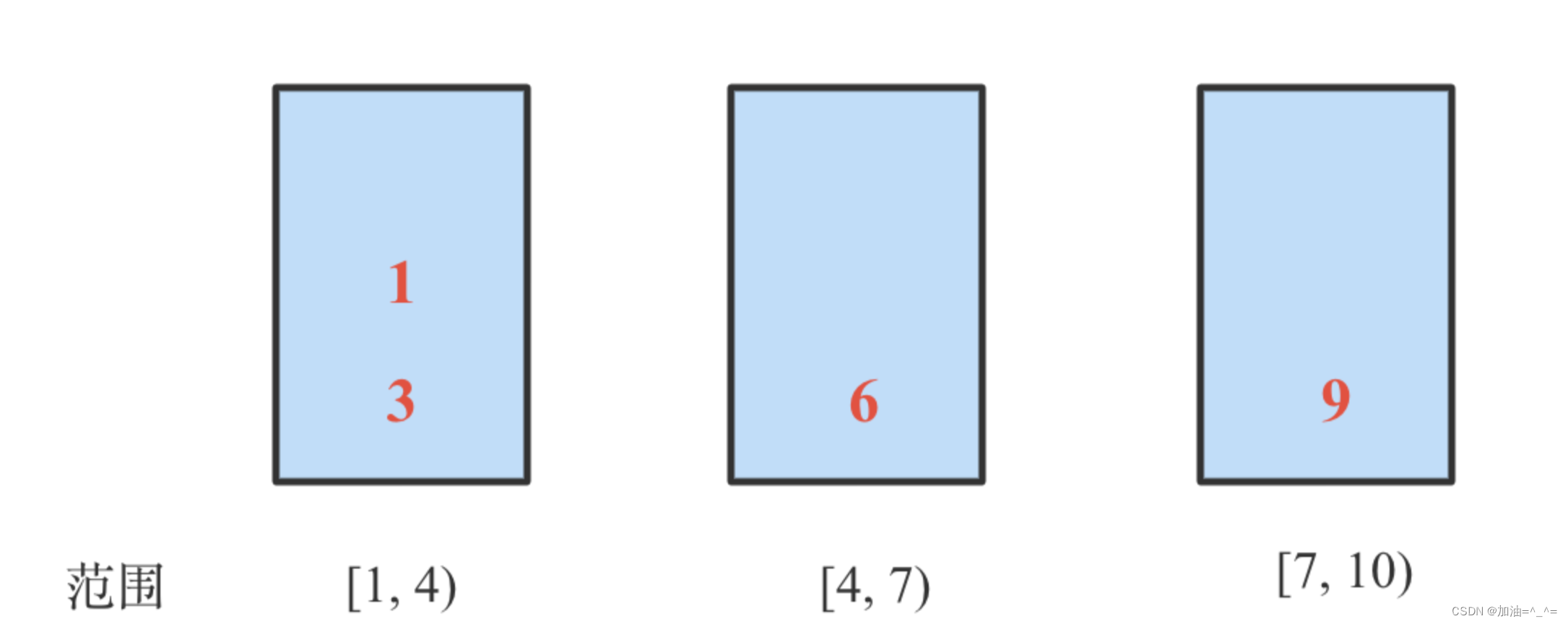

3）對各個桶中的數進行排序，得到如下圖所示：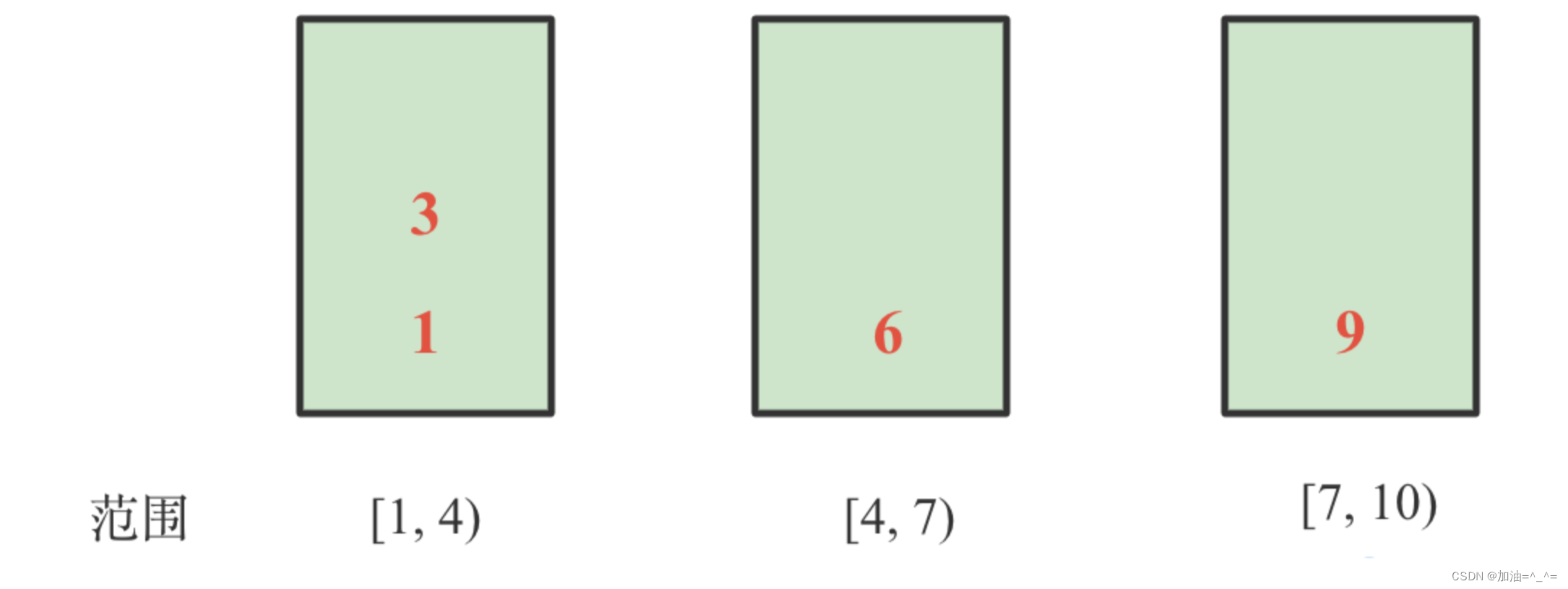

4）依次輸出各個排好序的桶中的數據，即為：1, 3, 6, 9
可見，最終得到了有序的排列。

代碼：?

    public static void barrelSort(int[] nums) {int n = nums.length;int max = 0, min = 0;//找出最大最小值for (int i = 0; i < n; i++) {if (nums[i] > max) {max = nums[i];}if (nums[i] < min) {min = nums[i];}}int size = (max - min) / n + 1;//獲取桶的個數，至少保證有一個int count = (max - min) / size + 1;//得知每個桶中存取數據范圍(相當于差值)List<Integer>[] barrel = new List[size];//初始化每個桶for (int i = 0; i < size; i++) {barrel[i] = new ArrayList<>();}//掃描一遍數組，把數放在對應的桶里面for (int i = 0; i < n; i++) {int index = (nums[i] - min) / size;//定位第幾個桶barrel[index].add(nums[i]);}//對同種每個數據進行排序，這里使用快排for (int i = 0; i < size; i++) {barrel[i].sort(null);//默認就是升序排序，不需要使用比較器}//一次出桶int index = 0;for (int i = 0; i < size; i++) {for (int j = 0; j < barrel[i].size(); j++) {nums[index++] = barrel[i].get(j);}}}public static void main(String[] args) {int[] nums = {19,27,35,43,31,22,54,66,78};barrelSort(nums);for (int i = 0; i < nums.length; i++) {System.out.print(nums[i] + " ");}}
}

時間復雜度分析：?

最好時間復雜度：O（n + k）

????????其中k為桶的個數。即當數據是均勻分散排列的，那么每個桶分到的數據個數都是一樣的，這個步驟需要O(k)的時間復雜度，在對每個桶進行排序的時候，最好情況下是數據都已經是有序的了，那么最好的排序算法的時間復雜度會是O(n)，因此總的時間復雜度是?O(n + k)?。

最壞時間復雜度：O（n^2）

????????當對每個桶中的數據進行排序的時候，所使用的排序算法，最壞情況下是O(n^2).

平均時間復雜度：O（n）

基數排序：

基數排序的思想：