一、二元關系的定義和表示
什么是二元關系?對集合A和B,A\timesB的任意子集R為A到B的一個二元關系。當A=B時,A\timesA的任一子集R稱為A上的一個二元關系。在不引起誤解的情況下,二元關系可簡稱關系。
若|A|=m,|B|=n,則A到B的二元關系共有2^{mn}個,A上的二元關系共有2^{m^{2}}個。
定義域與值域
關系的三種表示法:集合表示法、關系圖表示法、關系矩陣表示法

二、關系的運算
關系是有序對的集合,所以同樣可做集合運算,如并、交、補、差等
關系的復合:
關系的逆:


復合:兩個矩陣做布爾乘法運算
布爾乘法:普通矩陣乘法中加法變析取,乘法變合取
逆:矩陣轉置
三、關系的性質
自反性與反自反性

對稱性與反對稱性

傳遞性

四、關系的閉包
閉包的定義:添加最少的元素,使關系R具備自反性、或對稱性,或傳遞性,分別稱為自反閉包r(R),對稱閉包s(R),傳遞閉包t(R)。


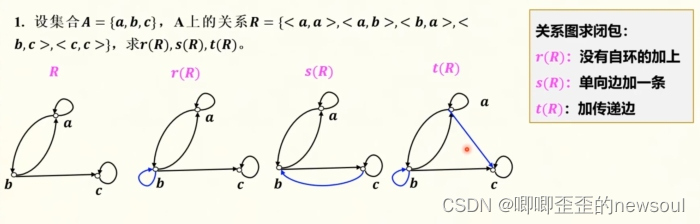 ?
?
?
?
?


: 現代IT管理的革命)


)



java開發工程師-機試題目/頌大技術面試總結/理工數傳 軟件開發一面二面面試總結/武漢智能視覺信息技術有限公司/高級)



維持黑框的思考)





詳解」2023年11月17日)