【機器學習聚類算法實戰-5】機器學習聚類算法之DBSCAN聚類、K均值聚類算法、分層聚類和不同度量的聚集聚類實例分析

🎩 歡迎來到技術探索的奇幻世界👨?💻

📜 個人主頁：@一倫明悅-CSDN博客

?🏻 作者簡介：?C++軟件開發、Python機器學習愛好者

🗣??互動與支持：💬評論?? ? ?👍🏻點贊?? ? ?📂收藏?? ? 👀關注+

如果文章有所幫助，歡迎留下您寶貴的評論，

點贊加收藏支持我，點擊關注，一起進步！

前言 ? ?

正文

01-?DBSCAN聚類算法簡介 ? ?

02-?基于K均值的顏色量化實戰 ? ?

03-?分層聚類：結構化區域與非結構化區域 ? ?

04-?不同度量的聚集聚類實戰 ? ?

總結

前言 ? ?

??????????DBSCAN（Density-Based Spatial Clustering of Applications with Noise）聚類算法是一種基于密度的聚類算法，能夠有效地發現任意形狀的聚類，并能夠處理噪聲數據。該算法通過定義特定半徑內的數據點數量來構建具有足夠密度的聚類，并將稀疏區域或孤立點識別為噪聲。DBSCAN算法的優勢在于無需指定聚類數目，適用于各種數據形狀和大小的數據集。

????????K均值聚類算法是一種基于距離的聚類算法，將數據點分為K個簇以最小化每個簇內數據點到簇中心的距離平方和。該算法需要提前指定簇的數量K，并通過隨機初始化簇中心和迭代更新樣本的簇分配來進行聚類。K均值聚類算法的優勢在于簡單易理解、實現方便，但對初始質心敏感，且對異常值敏感。

????????分層聚類是一種層次化的聚類方法，根據數據間的相似性逐步合并聚類簇，形成一個完整的聚類層次結構。分層聚類方法包括凝聚聚類（agglomerative clustering）和分裂聚類（divisive clustering）兩種主要策略。凝聚聚類從單個樣本開始，逐步合并最相似的聚類，形成一個樹狀結構；分裂聚類則從一個包含所有樣本的聚類開始，逐步分裂為子聚類。分層聚類的優勢在于可以同時得到不同層次的聚類結果，幫助分析數據的聚類結構。

????????不同度量的聚集實例分析包括了選擇不同的距離度量或相似性度量來計算數據點之間的距離，并應用于聚類算法中。常用的距離度量包括歐氏距離、曼哈頓距離、余弦相似度等，不同的度量方式會影響聚類結果的質量和形狀。選擇合適的度量方式對于聚類算法的效果至關重要，需要根據具體數據的特點和問題需求進行選擇。例如，在處理圖像數據時，可以選擇使用像素之間的歐氏距離；在自然語言處理領域，可以選擇余弦相似度度量文本之間的相似性。通過實例分析不同度量方式在聚類任務中的應用，可以更好地理解數據間的相似性和差異性，提高聚類算法的效果和準確性。

正文

01-?DBSCAN聚類算法簡介 ? ?

??????????DBSCAN（Density-Based Spatial Clustering of Applications with Noise）聚類算法是一種基于密度的聚類算法，能夠有效地發現任意形狀的聚類，并可以處理噪聲數據。下面是對DBSCAN聚類算法的詳細分析，包括原理和步驟：

????????原理分析：

????????DBSCAN算法基于以下兩個重要概念來實現聚類：

?????????核心對象（Core Point）：如果一個數據點的鄰域內至少包含指定數量的數據點（MinPts），則該點被認為是核心對象。

?????????直接密度可達（Directly Density Reachable）：如果一個數據點在另一個數據點的鄰域內，且另一個數據點是核心對象，則該數據點通過核心對象直接密度可達。????????

????????基于以上概念，DBSCAN算法將數據點分為三種類型：????????

????????核心對象：在其鄰域內至少包含 MinPts 個數據點的數據點。

????????邊界點：不是核心對象，但位于核心對象的鄰域內。

????????噪聲點（Noise Point）：既不是核心對象，也不是邊界點。

????????步驟分析：

????????參數設置：設定兩個參數，eps?表示鄰域的半徑，MinPts?表示一個核心對象所需的最少數據點個數。

????????核心對象識別：對數據集中的每個數據點進行遍歷，計算其鄰域內的數據點數目，標記核心對象。（核心對象滿足在其鄰域內至少包含 MinPts 個數據點）

????????聚類擴展：從任意未訪問的核心對象開始，探索其直接密度可達的數據點進行連接并形成一個聚類。若邊界點位于多個核心對象的鄰域內，則將其分配給其中一個核心對象的聚類

????????噪聲點處理：將未分配到任何聚類的噪聲點處理為離群點。

????????算法特點：

????????自動確定聚類數目：無需事先指定聚類數目，只需設定鄰域半徑?eps?和最小數據點數?MinPts。

????????適用于任意形狀的簇：DBSCAN能夠有效地捕捉數據中的任意形狀的聚類。

????????對噪聲數據魯棒：能夠將孤立點或噪聲數據識別為離群點，不會干擾聚類過程。

????????高效性：相對于K均值等算法，DBSCAN在處理大規模數據集時更為高效。

????????下面給出具體代碼分析應用過程：?這段代碼演示了如何使用DBSCAN算法對生成的樣本數據進行聚類，并對聚類結果進行評估和可視化。

首先，使用?make_blobs?生成了三個簇的樣本數據，并進行了標準化處理。
然后，通過?DBSCAN?對標準化后的數據進行聚類，設置了?eps=0.3?和?min_samples=10?作為參數。
計算了聚類結果中的核心樣本點，并對每個樣本點進行了標記。
使用不同的評估指標（如均勻性、完整性、V-measure 等）評估了聚類結果的質量。
最后，通過可視化展示了聚類結果。將核心點和邊界點以不同的大小和顏色進行繪制，用黑色表示噪聲點。

import numpy as npfrom sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler# #############################################################################
# Generate sample data
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4,random_state=0)X = StandardScaler().fit_transform(X)# #############################################################################
# Compute DBSCAN
db = DBSCAN(eps=0.3, min_samples=10).fit(X)
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_# Number of clusters in labels, ignoring noise if present.
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
n_noise_ = list(labels).count(-1)print('Estimated number of clusters: %d' % n_clusters_)
print('Estimated number of noise points: %d' % n_noise_)
print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels))
print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels))
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
print("Adjusted Rand Index: %0.3f"% metrics.adjusted_rand_score(labels_true, labels))
print("Adjusted Mutual Information: %0.3f"% metrics.adjusted_mutual_info_score(labels_true, labels))
print("Silhouette Coefficient: %0.3f"% metrics.silhouette_score(X, labels))# #############################################################################
# Plot result
import matplotlib.pyplot as plt# Black removed and is used for noise instead.
unique_labels = set(labels)
colors = [plt.cm.Spectral(each)for each in np.linspace(0, 1, len(unique_labels))]
for k, col in zip(unique_labels, colors):if k == -1:# Black used for noise.col = [0, 0, 0, 1]class_member_mask = (labels == k)xy = X[class_member_mask & core_samples_mask]plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),markeredgecolor='k', markersize=14)xy = X[class_member_mask & ~core_samples_mask]plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),markeredgecolor='k', markersize=6)plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.savefig("../5.png", dpi=500)

????????實例運行結果如下圖所示：

圖中不同顏色的點表示不同的聚類簇，同一簇內的點顏色相同。
大點表示核心樣本點，小點表示邊界點。
黑色的點表示噪聲點，即未分配到任何簇的樣本點。
圖像中心的聚類簇密集程度較高，周圍的樣本點則較為分散，符合DBSCAN對于密度聚類的特點。
通過圖像可以直觀地觀察到聚類結果，評估聚類算法的性能和有效性。

02-?基于K均值的顏色量化實戰 ? ?

?????????基于K均值的顏色量化是一種常用的圖像處理技術，可以將一幅彩色圖像中的顏色數量減少，從而減小圖像的尺寸，降低存儲和處理的復雜度。下面是對基于K均值的顏色量化的詳細分析：

????????原理分析：

數據準備：將彩色圖像中的每個像素看作是一個三維向量，表示紅、綠、藍（RGB）分量的取值。數據準備階段即將圖像中的所有像素點按照RGB值組織成一個數據集。
K均值算法：將數據集中的像素點以RGB向量的形式聚類成K個簇，使得每個像素點被分配到與之最近的簇中心，從而實現顏色壓縮。
迭代優化：迭代地更新簇中心，直至達到收斂條件（如中心點不再變化、迭代次數達到上限等）。
顏色替換：將每個簇的顏色替換為該簇內所有像素點的平均顏色值。

????????實現步驟：

初始化：隨機選擇K個像素點作為初始的簇中心。
簇分配：計算每個像素點與各個簇中心的距離，將其分配到最近的簇中心。
更新中心：更新每個簇中心為該簇內所有像素點的平均值。
迭代：重復步驟2和3直至滿足終止條件。
顏色替代：將每個像素點的顏色替換為其所屬簇的簇中心顏色。

????????算法特點：

簡單高效：K均值算法實現簡單，易于理解和實現。
需預先確定K值：K均值算法需要事先確定聚類的數量K，不同的K值可能導致不同的聚類結果。
對初始化敏感：簇中心的初始化對最終結果有較大影響，可能會陷入局部最優解。
適用性廣泛：K均值算法在顏色量化等應用領域效果較好，但對于異性方差較大的數據不太適用。

????????應用領域：

圖像壓縮：通過減少顏色數量，可以降低圖像的尺寸和存儲空間。
圖像處理：在圖像編輯中，顏色量化可以用于圖像風格遷移、圖像復原等領域。
數據可視化：顏色量化也常用于將圖像的顏色數目減少用于數據可視化等領域。

????????下面給出具體代碼分析應用過程：?這段代碼實現了基于K均值的顏色量化，并使用了scikit-learn庫中的KMeans模型進行顏色壓縮。以下是對代碼的簡要解釋和對生成的圖像的詳細分析：

加載中國宮殿的圖像，并將圖像轉換為浮點數表示，范圍在[0,1]之間。
將圖像轉換為2D的numpy數組，以便用于K均值算法。
隨機選擇1000個像素點的子樣本用于訓練K均值模型，并擬合模型。
使用訓練好的K均值模型對整個圖像進行顏色壓縮，并預測各像素點的顏色類別。
使用隨機選擇的顏色作為參考，對整個圖像進行顏色壓縮并預測顏色類別。
定義recreate_image()函數以重新構建壓縮后的圖像。
顯示原始圖像、K均值顏色壓縮后的圖像和隨機顏色壓縮后的圖像。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import pairwise_distances_argmin
from sklearn.datasets import load_sample_image
from sklearn.utils import shuffle
from time import timen_colors = 64# Load the Summer Palace photo
china = load_sample_image("china.jpg")# Convert to floats instead of the default 8 bits integer coding. Dividing by
# 255 is important so that plt.imshow behaves works well on float data (need to
# be in the range [0-1])
china = np.array(china, dtype=np.float64) / 255# Load Image and transform to a 2D numpy array.
w, h, d = original_shape = tuple(china.shape)
assert d == 3
image_array = np.reshape(china, (w * h, d))print("Fitting model on a small sub-sample of the data")
t0 = time()
image_array_sample = shuffle(image_array, random_state=0)[:1000]
kmeans = KMeans(n_clusters=n_colors, random_state=0).fit(image_array_sample)
print("done in %0.3fs." % (time() - t0))# Get labels for all points
print("Predicting color indices on the full image (k-means)")
t0 = time()
labels = kmeans.predict(image_array)
print("done in %0.3fs." % (time() - t0))codebook_random = shuffle(image_array, random_state=0)[:n_colors]
print("Predicting color indices on the full image (random)")
t0 = time()
labels_random = pairwise_distances_argmin(codebook_random,image_array,axis=0)
print("done in %0.3fs." % (time() - t0))def recreate_image(codebook, labels, w, h):"""Recreate the (compressed) image from the code book & labels"""d = codebook.shape[1]image = np.zeros((w, h, d))label_idx = 0for i in range(w):for j in range(h):image[i][j] = codebook[labels[label_idx]]label_idx += 1return image# Display all results, alongside original image
plt.figure(1)
plt.clf()
plt.axis('off')
plt.title('Original image (96,615 colors)')
plt.imshow(china)
plt.savefig("../3.png", dpi=500)
plt.figure(2)
plt.clf()
plt.axis('off')
plt.title('Quantized image (64 colors, K-Means)')
plt.imshow(recreate_image(kmeans.cluster_centers_, labels, w, h))
plt.savefig("../4.png", dpi=500)
plt.figure(3)
plt.clf()
plt.axis('off')
plt.title('Quantized image (64 colors, Random)')
plt.imshow(recreate_image(codebook_random, labels_random, w, h))
plt.savefig("../5.png", dpi=500)
plt.show()

????????實例運行結果如下圖所示：

原始圖像（96,615種顏色）：展示了原始彩色圖像，顏色細節豐富。
K均值顏色壓縮后的圖像（64種顏色）：經過K均值算法壓縮處理，僅采用64種顏色表達圖像，顏色數量減少，但整體色調保持。
隨機顏色壓縮后的圖像（64種顏色）：使用隨機選取的顏色進行壓縮后的圖像，色調會略有不同于K均值方法，但也達到了顏色量化的目的。

03-?分層聚類：結構化區域與非結構化區域 ? ?

?????????分層聚類是一種聚類分析方法，它通過逐步合并或分裂聚類來構建聚類層次結構。在圖像處理領域中，分層聚類可以針對圖像中的結構化區域（如邊緣、紋理等）和非結構化區域（如背景、平坦區域等）進行分析和處理。下面是對分層聚類在處理結構化區域與非結構化區域的詳細分析：

結構化區域和非結構化區域的特點：

結構化區域：通常指圖像中具有明顯紋理、邊緣、形狀等特征的區域，這些區域具有一定的規律性和重復性。
非結構化區域：指圖像中較為平坦、連續的區域，缺乏明顯的紋理和邊緣特征，整體呈現較為均勻的顏色分布。

分層聚類在處理結構化區域和非結構化區域的應用：

結構化區域：

特征提取：分層聚類可以幫助提取結構化區域的特征，如邊緣檢測、紋理分析等，從而實現對結構化區域的定位和描述。
分割和識別：通過分層聚類，可以將圖像中相似的結構化區域劃分到同一聚類中，并進一步實現目標分割和識別。

非結構化區域：

背景提取：分層聚類可以幫助識別并提取出圖像中的非結構化背景區域，實現對圖像中主體與背景的分離。
顏色量化：將非結構化區域進行聚類處理，可以實現對顏色的量化和壓縮，減少圖像中的細節和噪聲。

實現方法：

分層聚類算法選擇：常用的分層聚類算法包括層次聚類、BIRCH（Balanced Iterative Reducing and Clustering using Hierarchies）等，根據應用場景選擇適合的算法。
特征提取與表示：針對結構化區域和非結構化區域提取合適的特征向量，可以是顏色、紋理、邊緣等特征。
聚類處理：根據提取的特征向量進行分層聚類，構建聚類層次結構，將相似的區域合并或分裂。
結果分析和后處理：對于結構化區域，可以進一步處理提取的特征信息，對于非結構化區域，可以根據聚類結果進行后續處理，如背景提取、顏色量化等操作。

應用場景：

醫學圖像分析：對醫學圖像中的病變結構和正常組織進行區分和分析。
地圖圖像處理：識別地圖中的道路、水域等結構化區域以及其他地物。
圖像分割：將圖像分割為不同的結構和區域，便于進一步處理和分析。

????????通過分層聚類對結構化區域和非結構化區域進行分析和區分，有助于更好地理解圖像內容、實現圖像分割和特征提取，并在各種圖像處理應用中發揮作用。

?????下面給出具體代碼分析應用過程：這段代碼主要是使用了 scikit-learn 庫進行分層聚類（Hierarchical Clustering）的示例代碼，針對生成的瑞士卷數據集（Swiss Roll Dataset）進行了無連接約束和有連接約束兩種情況的聚類分析，并將結果通過 3D 散點圖可視化展示。下面對代碼和生成的圖像進行詳細分析：

首先，使用 make_swiss_roll 生成含有噪音的瑞士卷數據集 X，然后將其變窄處理。
接著，使用 AgglomerativeClustering 進行分層聚類。首先對無連接約束的情況進行聚類（ward 連接方式，將數據分為 6 類），計算耗時并輸出結果。
接著，根據數據結構構建連接度矩陣（這里使用的是最近的 10 個鄰居），再次使用 AgglomerativeClustering 進行有連接約束的聚類，同樣分為 6 類，計算耗時并輸出結果。
最后，根據聚類結果繪制兩幅3D散點圖，分別展示了無連接約束和有連接約束下的聚類效果，并在標題中顯示了計算耗時。

import time as time
import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d.axes3d as p3
from sklearn.cluster import AgglomerativeClustering
from sklearn.datasets import make_swiss_roll# #############################################################################
# Generate data (swiss roll dataset)
n_samples = 1500
noise = 0.05
X, _ = make_swiss_roll(n_samples, noise=noise)
# Make it thinner
X[:, 1] *= .5# #############################################################################
# Compute clustering
print("Compute unstructured hierarchical clustering...")
st = time.time()
ward = AgglomerativeClustering(n_clusters=6, linkage='ward').fit(X)
elapsed_time = time.time() - st
label = ward.labels_
print("Elapsed time: %.2fs" % elapsed_time)
print("Number of points: %i" % label.size)# #############################################################################
# Plot result
fig = plt.figure()
ax = p3.Axes3D(fig)
ax.view_init(7, -80)
for l in np.unique(label):ax.scatter(X[label == l, 0], X[label == l, 1], X[label == l, 2],color=plt.cm.jet(np.float(l) / np.max(label + 1)),s=20, edgecolor='k')
plt.title('Without connectivity constraints (time %.2fs)' % elapsed_time)
plt.savefig("../4.png", dpi=500)# #############################################################################
# Define the structure A of the data. Here a 10 nearest neighbors
from sklearn.neighbors import kneighbors_graph
connectivity = kneighbors_graph(X, n_neighbors=10, include_self=False)# #############################################################################
# Compute clustering
print("Compute structured hierarchical clustering...")
st = time.time()
ward = AgglomerativeClustering(n_clusters=6, connectivity=connectivity,linkage='ward').fit(X)
elapsed_time = time.time() - st
label = ward.labels_
print("Elapsed time: %.2fs" % elapsed_time)
print("Number of points: %i" % label.size)# #############################################################################
# Plot result
fig = plt.figure()
ax = p3.Axes3D(fig)
ax.view_init(7, -80)
for l in np.unique(label):ax.scatter(X[label == l, 0], X[label == l, 1], X[label == l, 2],color=plt.cm.jet(float(l) / np.max(label + 1)),s=20, edgecolor='k')
plt.title('With connectivity constraints (time %.2fs)' % elapsed_time)
plt.savefig("../5.png", dpi=500)
plt.show()

????????實例運行結果如下圖所示：

無連接約束聚類結果：圖像中展示了數據點按照聚類結果著色，并在三維空間中展示其分布情況。不同顏色代表不同的聚類簇，展示了數據點的聚類效果。
有連接約束聚類結果：同樣是根據聚類結果著色展示數據點的分布情況，不同顏色代表不同的聚類簇。由于考慮了數據點之間的連接性，聚類效果可能會有所不同。

04-?不同度量的聚集聚類實戰 ? ?

?????????在數據挖掘和機器學習領域中，聚集聚類（Agglomerative Clustering）是一種常見的聚類算法，它通過不斷地將最相近的數據點或簇進行合并來構建聚類結構。在聚集聚類中，存在多種不同的度量方法用于衡量數據點之間的相似性或距離，從而影響最終的聚類結果。以下是一些常用的度量方法：

歐氏距離（Euclidean Distance）：最常見的距離度量方法之一，計算兩個數據點之間的直線距離。歐氏距離適用于數據特征為連續值的情況。

曼哈頓距離（Manhattan Distance）：也稱為城市街區距離，計算兩個數據點在各個坐標軸上的距離總和。適用于特征為連續值的情況。

切比雪夫距離（Chebyshev Distance）：計算兩個數據點在各個坐標軸上的最大差值。適用于處理數據縮放不一致的情況。

閔可夫斯基距離（Minkowski Distance）：歐氏距離和曼哈頓距離的泛化形式，可以通過參數來控制距離的計算方式。

余弦相似度（Cosine Similarity）：用于衡量兩個向量之間的夾角余弦值，而非距離，適用于處理文本數據或稀疏數據。

????????選擇合適的距離度量方法對聚集聚類的結果影響巨大，不同的數據特點和應用場景可能需要不同的度量方法來獲得最佳的聚類效果。在實際應用中，可以根據數據的特征和領域知識來選擇合適的距離度量方法，以及調整算法參數來優化聚類結果。

?????下面給出具體代碼分析應用過程：這段代碼主要是對生成的波形數據進行聚類分析，并使用不同的距離度量（余弦距離、歐氏距離、曼哈頓距離）來比較聚類結果。代碼中的主要步驟包括：

生成具有三種波形模式的數據集，每種模式有30個樣本。
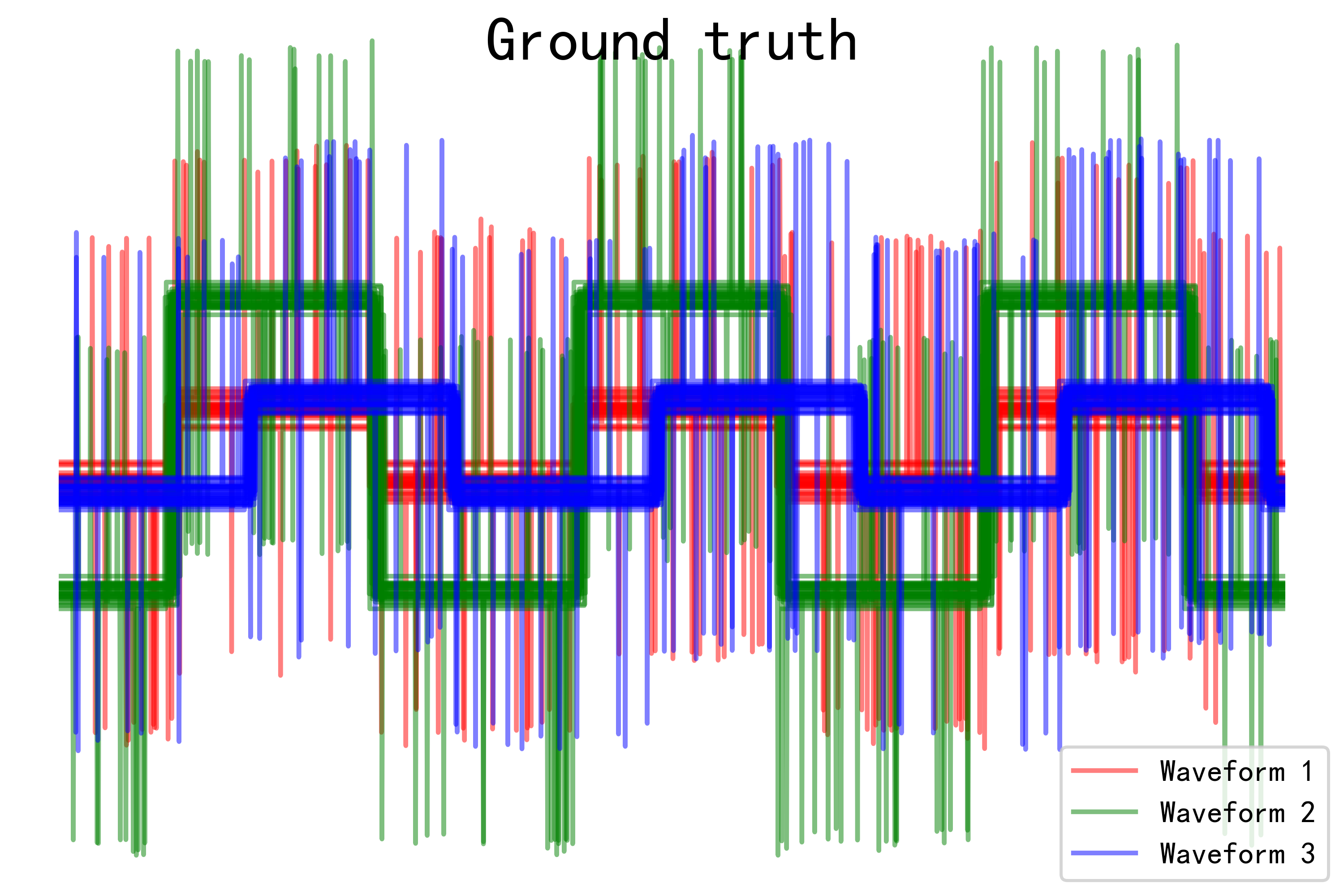
繪制基本波形數據的真實標簽情況，展示每種波形模式的數據分布情況。
計算不同波形類別之間的平均距離，并繪制熱圖展示不同度量方式下的類間距離情況。
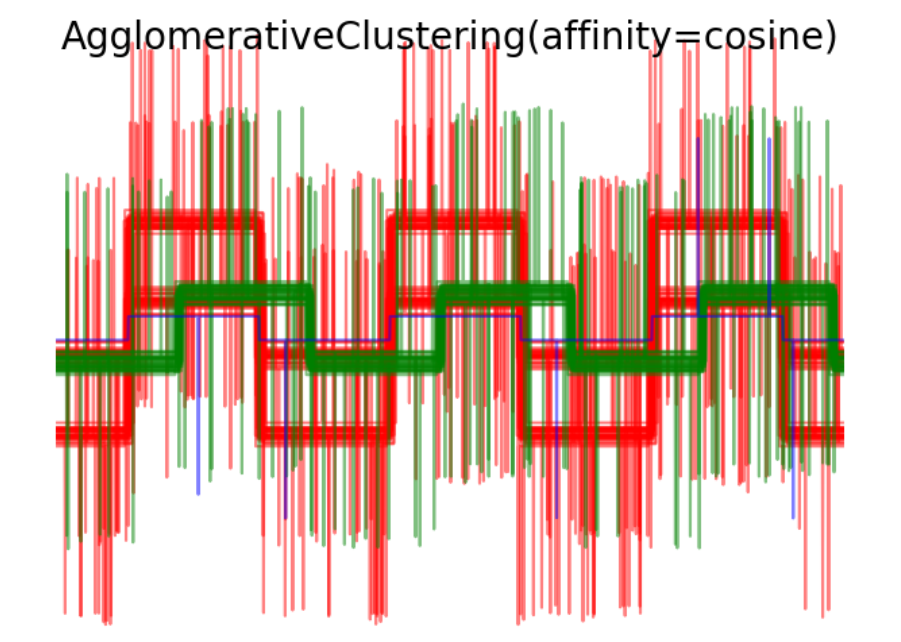
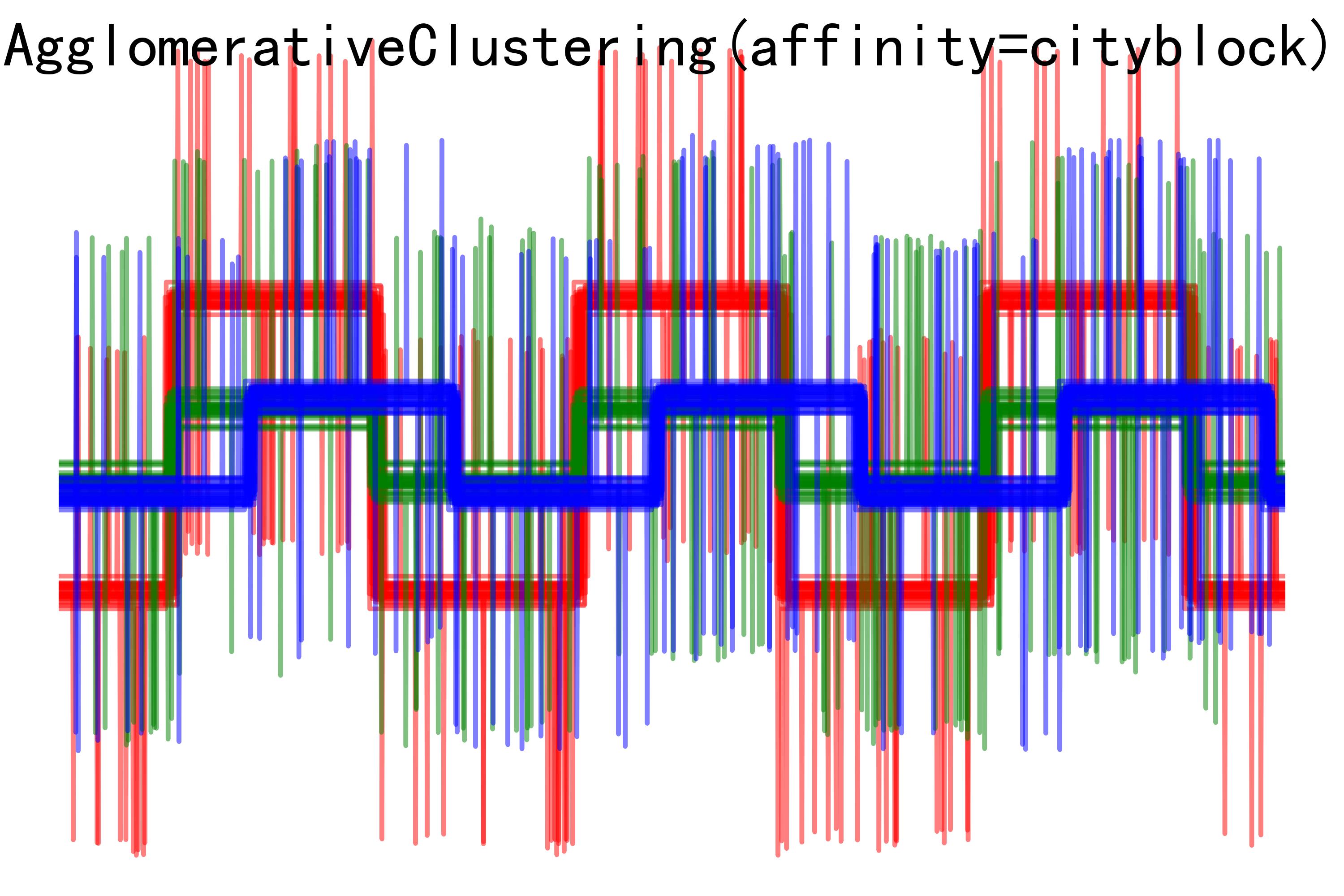
使用層次聚類算法（Agglomerative Clustering）對數據進行聚類，分別使用余弦距離、歐氏距離、曼哈頓距離進行聚類，并繪制聚類結果圖像。

import matplotlib.pyplot as plt
import numpy as npfrom sklearn.cluster import AgglomerativeClustering
from sklearn.metrics import pairwise_distancesnp.random.seed(0)# Generate waveform data
n_features = 2000
t = np.pi * np.linspace(0, 1, n_features)def sqr(x):return np.sign(np.cos(x))X = list()
y = list()
for i, (phi, a) in enumerate([(.5, .15), (.5, .6), (.3, .2)]):for _ in range(30):phase_noise = .01 * np.random.normal()amplitude_noise = .04 * np.random.normal()additional_noise = 1 - 2 * np.random.rand(n_features)# Make the noise sparseadditional_noise[np.abs(additional_noise) < .997] = 0X.append(12 * ((a + amplitude_noise)* (sqr(6 * (t + phi + phase_noise)))+ additional_noise))y.append(i)X = np.array(X)
y = np.array(y)n_clusters = 3labels = ('Waveform 1', 'Waveform 2', 'Waveform 3')# Plot the ground-truth labelling
plt.figure()
plt.axes([0, 0, 1, 1])
for l, c, n in zip(range(n_clusters), 'rgb',labels):lines = plt.plot(X[y == l].T, c=c, alpha=.5)lines[0].set_label(n)plt.legend(loc='best')plt.axis('tight')
plt.axis('off')
plt.suptitle("Ground truth", size=20)
plt.savefig("../5.png", dpi=500)# Plot the distances
for index, metric in enumerate(["cosine", "euclidean", "cityblock"]):avg_dist = np.zeros((n_clusters, n_clusters))plt.figure(figsize=(5, 4.5))for i in range(n_clusters):for j in range(n_clusters):avg_dist[i, j] = pairwise_distances(X[y == i], X[y == j],metric=metric).mean()avg_dist /= avg_dist.max()for i in range(n_clusters):for j in range(n_clusters):plt.text(i, j, '%5.3f' % avg_dist[i, j],verticalalignment='center',horizontalalignment='center')plt.imshow(avg_dist, interpolation='nearest', cmap=plt.cm.gnuplot2,vmin=0)plt.xticks(range(n_clusters), labels, rotation=45)plt.yticks(range(n_clusters), labels)plt.colorbar()plt.suptitle("Interclass %s distances" % metric, size=18)plt.tight_layout()
plt.savefig("../4.png", dpi=500)# Plot clustering results
for index, metric in enumerate(["cosine", "euclidean", "cityblock"]):model = AgglomerativeClustering(n_clusters=n_clusters,linkage="average", affinity=metric)model.fit(X)plt.figure()plt.axes([0, 0, 1, 1])for l, c in zip(np.arange(model.n_clusters), 'rgbk'):plt.plot(X[model.labels_ == l].T, c=c, alpha=.5)plt.axis('tight')plt.axis('off')plt.suptitle("AgglomerativeClustering(affinity=%s)" % metric, size=20)plt.savefig("../3.png", dpi=500)
plt.show()

????????實例運行結果如下圖所示：

Ground truth圖像：展示了真實標簽下每種波形模式的數據分布情況，可以清晰地看到不同波形之間的差異。
Interclass distances熱圖：展示了不同波形類別之間的平均距離，淺色表示距離較遠，深色表示距離較近，有助于比較不同距離度量方式下的類間相似性。
AgglomerativeClustering聚類結果圖像：展示了使用不同距禈度量方式進行聚類后的結果。每種波形模式使用不同顏色表示，可以觀察到不同聚類方法下對數據的聚類效果。

總結

??????????在機器學習領域，常用的聚類算法包括DBSCAN聚類算法、K均值聚類算法、以及分層聚類算法。這些算法在處理不同類型的數據和應用場景中都有各自的優勢和適用性。

DBSCAN聚類算法（Density-Based Spatial Clustering of Applications with Noise）：

優點：能夠發現任意形狀的聚類，對噪聲數據比較魯棒。
工作原理：通過定義鄰域內的數據點密度來確定聚類，從而將高密度區域劃分為一個聚類，并能夠有效處理密度不均勻的數據集。

K均值聚類算法（K-Means Clustering）：

優點：簡單且高效，適用于大規模數據集。
工作原理：將數據點劃分為K個簇，通過不斷迭代更新簇的中心點和重新分配數據點來最小化簇內的方差。

分層聚類算法（Hierarchical Clustering）：

優點：能夠構建聚類簇之間的層次結構，不需要預先指定簇的數量。
工作原理：通過不斷合并或分裂數據點或簇來構建聚類層次結構，可分為凝聚性層次聚類和分裂性層次聚類兩種方法。

不同度量的聚集：

聚集聚類是一種基于簇的層次聚類算法，采用不同的距離或相似度度量方法來決定簇之間的合并順序。
不同度量方法會影響聚類的結果，常用的度量包括歐氏距離、曼哈頓距離、切比雪夫距離、閔可夫斯基距離和余弦相似度等。

????????總的來說，選擇適合數據特點和需求的聚類算法和距離度量方法是十分重要的。DBSCAN適用于發現任意形狀的聚類，K均值適用于均衡分布的數據，分層聚類適用于構建聚類層次結構。同時，根據數據的特點和任務需求選擇合適的距離度量方法也是關鍵的一步。