435.無重疊區間

思路

為了使區間盡可能的重疊所以排序來使區間盡量的重疊，使用左邊界排序來統計重疊區間的個數與452. 用最少數量的箭引爆氣球恰好相反。

代碼

class Solution {public int eraseOverlapIntervals(int[][] intervals) {Arrays.sort(intervals,(a,b)->Integer.compare(a[0],b[0]));int count = 0;for (int i = 1; i < intervals.length; i++) {if(intervals[i-1][1] > intervals[i][0]){count++;intervals[i][1] = Math.min(intervals[i-1][1],intervals[i][1]);}}return  count;}
}

763.劃分字母區間

思路

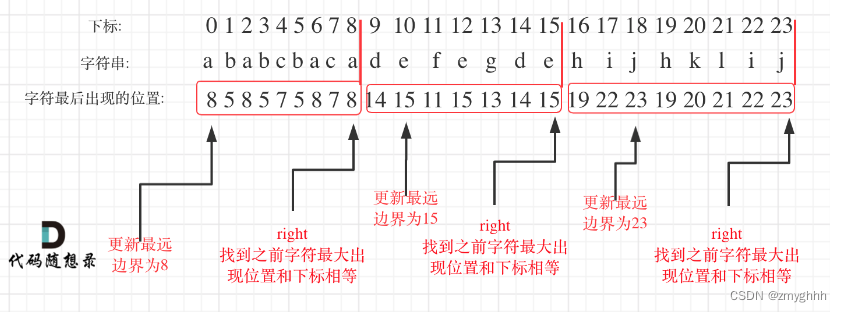
首先想到了回溯但是使用回溯依然沒有思路，在遍歷的過程中相當于是要找每一個字母的邊界，如果找到之前遍歷過的所有字母的最遠邊界，說明這個邊界就是分割點了。此時前面出現過所有字母，最遠也就到這個邊界了。

可以分為如下兩步：

• 統計每一個字符最后出現的位置
• 從頭遍歷字符，并更新字符的最遠出現下標，如果找到字符最遠出現位置下標和當前下標相等了，則找到了分割點

代碼

class Solution {public List<Integer> partitionLabels(String s) {List<Integer> list = new LinkedList<>();int [] hash = new int[27];char [] chars = s.toCharArray();for (int i = 0; i < chars.length; i++) {hash[chars[i] - 'a'] = i;}int left = 0,right = 0 ;for (int i = 0; i < chars.length; i++) {right = Math.max(right , hash[chars[i] - 'a']);if(i == right){list.add(right -left +1);left = i+1;}}return list;}
}

56. 合并區間

思路

本題的本質其實還是判斷重疊區間問題。452. 用最少數量的箭引爆氣球?(opens new window)和?435. 無重疊區間都是判斷區間重疊，區別就是判斷區間重疊后的邏輯，本題是判斷區間重貼后要進行區間合并。

代碼

class Solution {public int[][] merge(int[][] intervals) {LinkedList<int[]> res = new LinkedList<>();Arrays.sort(intervals, (o1, o2) -> Integer.compare(o1[0], o2[0]));res.add(intervals[0]);for (int i = 1; i < intervals.length; i++) {if (intervals[i][0] <= res.getLast()[1]) {int start = res.getLast()[0];int end = Math.max(intervals[i][1], res.getLast()[1]);res.removeLast();res.add(new int[]{start, end});}else {res.add(intervals[i]);}}return res.toArray(new int[res.size()][]);}
}

738.單調遞增的數字

思路

貪心算法

例如98，一旦出現strNum[i - 1] > strNum[i]的情況（非單調遞增），首先想讓strNum[i - 1]--，然后strNum[i]給為9，這樣這個整數就是89，即小于98的最大的單調遞增整數。

此時是從前向后遍歷還是從后向前遍歷呢？

從前向后遍歷的話，遇到strNum[i - 1] > strNum[i]的情況，讓strNum[i - 1]減一，但此時如果strNum[i - 1]減一了，可能又小于strNum[i - 2]。

數字：332，從前向后遍歷的話，那么就把變成了329，此時2又小于了第一位的3了，真正的結果應該是299。

那么從后向前遍歷，就可以重復利用上次比較得出的結果了，從后向前遍歷332的數值變化為：332 -> 329 -> 299

class Solution {public int monotoneIncreasingDigits(int n) {String s = String.valueOf(n);char[] chars = s.toCharArray();int start = s.length();for (int i = s.length() - 2; i >= 0; i--) {if (chars[i] > chars[i + 1]) {chars[i]--;start = i+1;}}for (int i = start; i < s.length(); i++) {chars[i] = '9';}return Integer.parseInt(String.valueOf(chars));}
}

968.監控二叉樹

思路

題目示例中的攝像頭都沒有放在葉子節點上！這是很重要的一個線索，攝像頭可以覆蓋上中下三層，如果把攝像頭放在葉子節點上，就浪費的一層的覆蓋。

所以把攝像頭放在葉子節點的父節點位置，才能充分利用攝像頭的覆蓋面積。

為什么不從頭結點開始看起呢，為啥要從葉子節點看呢？

因為頭結點放不放攝像頭也就省下一個攝像頭， 葉子節點放不放攝像頭省下了的攝像頭數量是指數階別的。（也算是一個貪心）

局部最優：讓葉子節點的父節點安攝像頭，所用攝像頭最少，

整體最優：全部攝像頭數量所用最少！

思路就是從低到上，先給葉子節點父節點放個攝像頭，然后隔兩個節點放一個攝像頭，直至到二叉樹頭結點。

在二叉樹中如何從低向高推導呢？

可以使用后序遍歷也就是左右中的順序，這樣就可以在回溯的過程中從下到上進行推導了。左孩子的返回值，右孩子的返回值，即left 和 right， 以后推導中間節點的狀態

難點

每個節點可能有幾種狀態：

有如下三種：

• 該節點無覆蓋（無攝像頭）
• 本節點有攝像頭
• 本節點有覆蓋（無攝像頭）

空節點的狀態只能是有覆蓋

為了讓攝像頭數量最少，我們要盡量讓葉子節點的父節點安裝攝像頭，這樣才能攝像頭的數量最少。

那么空節點不能是無覆蓋的狀態，這樣葉子節點就要放攝像頭了，空節點也不能是有攝像頭的狀態，這樣葉子節點的父節點就沒有必要放攝像頭了，而是可以把攝像頭放在葉子節點的爺爺節點上。

主要有如下四類情況：

• 情況1：左右節點都有覆蓋

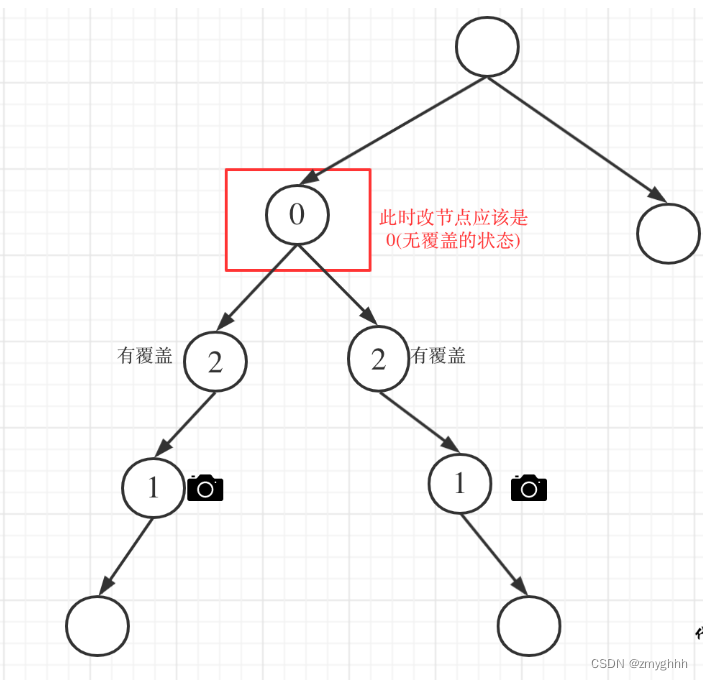
• 情況2：左右節點至少有一個無覆蓋的情況：中間節點（父節點）應該放攝像頭

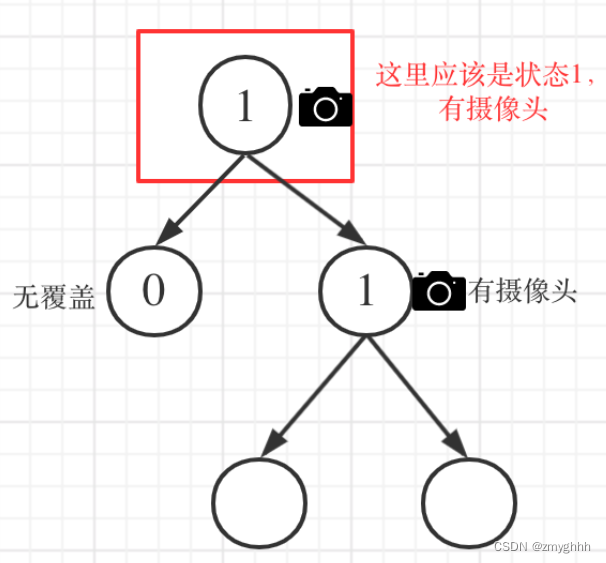
如果left == 1, right == 0 怎么辦？其實這種條件在情況2中已經判斷過了，如圖：

• 情況3：左右節點至少有一個有攝像頭：左右孩子節點有一個有攝像頭了，那么其父節點就應該是2（覆蓋的狀態）
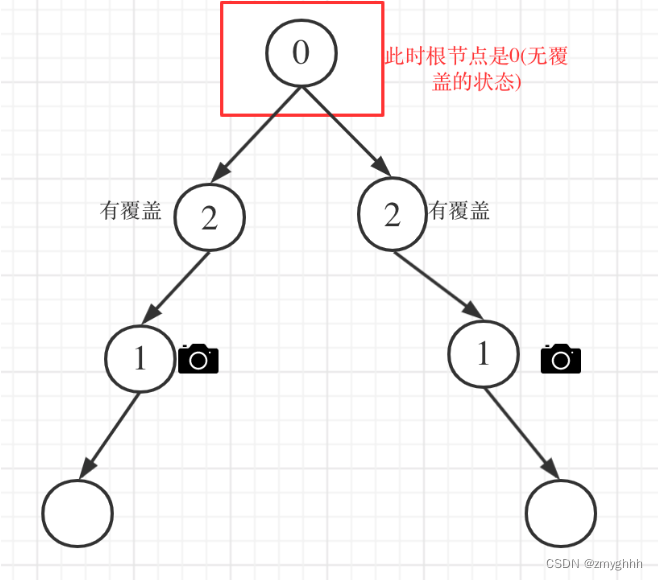
• 情況4：頭結點沒有覆蓋
• 

代碼

class Solution {int result = 0 ;public int minCameraCover(TreeNode root) {if(traversal(root) == 0){result++;}return result;}/**節點的狀態值：0 表示無覆蓋1 表示 有攝像頭2 表示有覆蓋后序遍歷，根據左右節點的情況,來判讀 自己的狀態*/public int traversal(TreeNode root){if(root == null) return 2;int left = traversal(root.left);int right = traversal(root.right);if(left==2 && right==2) return 0;if(left == 0 || right ==0){result++;return 1;}if(left == 1 || right ==1){return 2;}return -1;}
}