摘要

基于模型的識別和運動跟蹤依賴于解決投影和模型參數，使其最佳適應匹配的2D圖像特征的3D模型的能力。本文將當前的參數求解方法擴展到處理具有任意曲面和任意數量的內部參數（表示關節、可變尺寸或表面變形）的對象。開發了數值穩定化方法，考慮了圖像測量中固有的不準確性，并允許在匹配數小于未知參數數時確定有用的解決方案。使用Levenberg-Marquardt方法始終確保解決方案的收斂性。這些技術使基于模型的視覺能夠應用于比以前的方法更廣泛的問題類別。它們的應用被證明可以用于跟蹤曲線、參數化對象的運動。

1 引言

基于模型的視覺允許在視覺解釋過程中利用對特定對象形狀和外觀的先驗知識。通過識別模型和從圖像中提取的特征之間的一致部分匹配，可進行可靠的識別，從而使系統能夠推斷出比圖像中明確可用信息更多的場景信息。通過提供感知和場景組件先驗知識之間的聯系，基于模型的識別是視覺潛在應用的一個重要組成部分。

基于模型的視覺的一個重要組成部分是解決所有視點和模型參數的值，以便將模型最佳擬合到一些匹配的圖像特征中。這一點很重要，因為它允許一些初步的匹配約束模型其他特征的位置，從而生成新的匹配，可以用來驗證或拒絕初始解釋。通過考慮匹配過程中所有可用的定量信息來約束未知參數，可以極大地提高這一過程和最終解釋的可靠性。此外，參數確定對于識別對象子類別、解釋關節或靈活對象的圖像以及機器人與對象的交互是必要的。

在大多數情況下，可以從單個2D圖像的匹配解決3D模型的所有未知參數。然而，在某些情況下，例如當模型的大小和距離都未知時，通過同時將模型擬合到從多個視點拍攝的圖像中，可以大大提高參數確定的準確性。此處介紹的方法可以在任一情況下使用。

圖像中模型特征的投影位置是視點和模型參數的非線性函數。因此，解決方案基于牛頓線性化和迭代的方法執行最小二乘最小化。通過結合一個包含每個參數不確定性范圍的先驗模型和每個圖像測量標準差的估計的穩定化方法，增加了一個穩定化方法。這允許對于在其他情況下會是欠定或病態的問題獲得有用的近似解決方案。此外，Levenberg-Marquardt方法被用來始終強制解決方案收斂到局部最小值。這些技術都已經作為基于模型的運動跟蹤系統的一部分進行了實施和測試，并且它們被發現是可靠和高效的。

2 先前的方法

解決視點和模型參數的嘗試可以追溯到Roberts的工作[30]。盡管他的解決方法是針對特定類別的對象，比如矩形塊，但Roberts清楚地了解到通過定量參數確定來使視覺對缺失和嘈雜數據具有魯棒性的價值。然而，很不幸，在其初始發表之后的許多年里，很少有人試圖在這項工作的基礎上進行進一步研究。

1980年，作者[19]提出了一種使用牛頓方法進行非線性最小二乘最小化解決視點和模型2參數的通用技術。自那時以來，這種方法已經成功地應用于許多應用中，并且它也為本文所介紹的工作提供了起點。該方法在魯棒的基于模型的識別中的應用已經由Lowe [20, 21, 22]、McIvor [26]以及Worrall、Baker和Sullivan [34]進行了描述。Bray [2]將該方法應用于剛性對象的基于模型的運動跟蹤。Ishii等人[14]描述了將此工作應用于從手腕上安裝的LED目標的單視圖跟蹤方向和位置的問題。他們的論文提供了一種詳細的分析，顯示了良好的準確性和穩定性。Goldberg和Lowe [8]描述了應用和測試這個問題的一些更先進的數值方法。

近年來，關于基于模型的視覺參數求解的論文數量大幅增加，大部分工作致力于解決剛性對象的視點參數。Liu等人[18]和Kumar [15]通過將旋轉解決方案與平移解決方案分離，研究了解決視點參數的替代迭代方法。然而，Kumar表明，在存在嘈雜數據的情況下，這種方法導致參數估計明顯更差。因此，他采用了與上述工作中使用的類似的同時最小化方法。基于使用消除方法提供初始問題表述的完全不同的方法由Ponce和Kriegman [29]提出。這也是基于牛頓方法進行最終參數確定的最小二乘最小化。

Haralick等人[11]嘗試了使用迭代重新加權等魯棒方法，以允許由不正確匹配引起的異常值。然而，他們的結果表明，即使在20個正確匹配中存在一個異常值，重新加權后預期誤差也會大幅增加。本文使用的替代方法是提供一個更高級別的搜索過程，當第一組匹配未能產生準確的模型擬合時，考慮其他匹配集合。

2.1 多解決方案的問題

已經發表了大量關于表征解決六個視點參數所需的最小數據量以及解決僅有這些最小數據時可能出現的多個解決方案的工作。Fischler和Bolles [6]表明，對于將3個模型點匹配到3個圖像點的問題，可能會出現最多四個解，并且他們給出了識別每個解的程序。Horaud等人[12]給出了相應的4點問題的解，該問題在某些情況下也可能有多個解。Huttenlocher和Ullman [13]表明，對于正交投影，三點問題有一個簡單的解決方案，這對于一些應用來說是足夠接近透視投影的。他們使用術語“對齊”來指代模型擬合過程中視點參數的解。對于許多實際應用而言，Dhome等人[4]給出了解決匹配3個模型線到3個圖像線的問題的所有解的方法，這對于生成本文中使用的迭代技術的起始位置特別有用，當存在多個解決方案時。

確定所有可能的精確解的這項工作無疑對某些特定的視覺應用非常重要，但對于一般的基于模型的視覺的實際參數確定來說，這可能不是最佳方法。這些方法的一個問題是它們沒有解決病態問題的問題。即使問題只有一個解析解，實踐中也經常具有足夠病態性，以具有大量和范圍廣泛的解。其次，所有這些方法都處理六個視點參數的特定屬性，并且很少可能擴展到處理任意數量的內部模型參數。最后，這些方法未能解決解決方案受到限制時該如何處理的問題。本文描述的穩定方法允許在問題受到限制時獲得近似解決方案，而當模型包含許多參數時，這種情況經常會發生。

或許相信不必確定所有可能解決方案的最具說服力的原因是，人類視覺顯然也無法做到這一點。著名的內克立方體幻覺說明了人類視覺在確定視點參數時很容易陷入局部最小值，并且似乎無法同時考慮多個解。Rock [31]總結了人類感知似乎始終在面對完全不確定的連續變量時采用一種特定的感知方式。感知可以在面對新信息時突然轉變到新的穩定位置，這些信息可能來自于視覺系統的其他組件（注意力）以及外部刺激。這種行為與一種穩定的最小化方法來確定參數值是一致的，在該方法中，當新信息可用時，過程可以從新的起始點開始。盡管人類視覺可能陷入錯誤的局部最小值，但在大多數識別問題中表現非常出色，這表明在確定模型參數時，局部最小值可能并不是一個主要問題。

值得注意的是，當有準確的三維圖像數據可用時（比如來自掃描激光測距儀），參數求解問題就會變得更加簡單，因為這樣可以避免由投影引起的某些非線性。Faugeras & Hebert [5]和Grimson & Lozano-P′erez [10]給出了解決這個問題的例子。然而，在本文中，我們將注意力限制在將三維模型擬合到二維圖像特征上。

3 Object and scene modeling

大多數基于模型的視覺研究都是基于簡單的多面體3D對象模型。雖然它們易于處理，但顯然無法代表許多真實世界的對象。一些研究是基于從某些體積原始構建的模型，其中最值得注意的是廣義圓柱體 [1, 3]和超橢球體 [27]。雖然這些模型吸引人的原因是它們能夠捕捉常見的對稱性并用少量參數表示某些形狀，但它們不適合于建模許多不具有這些原始體內所包含的規則性的自然物體。最徹底研究如何表示任意對象的視覺外觀的領域是計算機圖形學。從該領域的發展中得到的教訓非常明確：復雜的解析表示已經被簡單的局部近似所取代，成為成本效益最高的解決方案。在渲染之前，用于模型表示的最常見的局部近似形式是多邊形表面補丁，以及與顯示相關的各種參數的適當插值。由于任意函數都可以通過使用足夠多的簡單局部近似來近似到任意精度，因此在這個表示水平上唯一重要的問題是效率。計算機圖形學的經驗傾向于表明，用于簡單線性近似所需的近似補丁數量的增加遠遠超過了它們可以被操作的速度。當然，更復雜的樣條曲線和體積原始體仍然可以用于模型輸入或其他更高級別的推理。

與計算機圖形學一樣，視覺是建立在近似藝術之上的。當然，重要的是要近似適當的測量，否則一個量的近似可能會引入其導數或其他依賴于它的函數中不希望的誤差。在基于模型的視覺中，我們關注的是正確地近似那些將與圖像測量匹配的函數。對于基于邊緣的匹配，這將包括邊緣的投影位置、切線、曲率和不連續性。如果匹配的是陰影或表面屬性，那么還必須近似表面曲率。我們已經開發了一個建模系統，允許將這些量建模為視點和內部模型參數的函數，以任意所需的精度使用于高效的參數求解。

盡管基于模型的視覺可以從計算機圖形學中學到很多，但建模要求也存在重要的差異。在基于模型的匹配到二維圖像中，模型是與導出的圖像特征進行匹配，而不是用于生成密集的表面描述。例如，直接計算遮擋輪廓的位置是很重要的，在許多為計算機圖形學開發的建模系統中是不可能的。由于模型在匹配過程的內循環中進行投影和操作，因此必須利用視覺領域特有的所有可能的效率來源。此外，某些數量在圖形應用程序中不存在，例如與模型參數相關的導數，必須以高效的方式表示和計算。因為這些原因，必須開發一個面向視覺的建模系統，而不是采用現有的為圖形學開發的系統。

已經開發了一種簡單的建模語言，可用于描述用于基于模型的視覺的任意模型及其內部參數。該語言用于定義和命名三維點、邊和表面補丁，以及定義旋轉和平移的模型參數。每個模型點都是坐標變換樹中的葉子，該樹代表不同參數指定的先前旋轉和平移的任意組合（見圖1）。

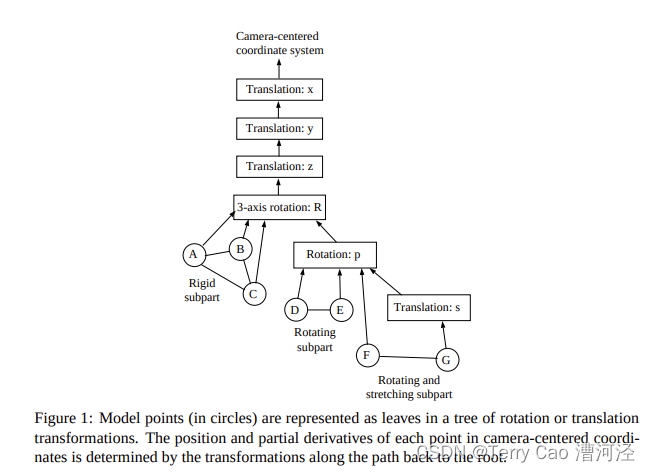
相同的機制用于處理視點參數和內部模型參數，因此該樹的根代表相機坐標系。當從該語言的描述構建內部模型時，會構建一個密集的指針網絡，將每個邊元素鏈接到其相鄰的表面補丁和端點。使用緩存機制，以便只計算每個表面多邊形的可見性和每個點的投影一次，與大多數圖形建模系統不同。由于表面或線上的每個點可以通過連接到不同框架來獨立移動，因此可以指定模型的任意靈活運動。例如，圖1中連接點F和G的線可以在參數s的影響下伸展，并在參數p的影響下與另一個模型子部分一起旋轉（每個平移框架指定一個平移方向，每個旋轉指定一個旋轉軸）。邊緣根據它們是否位于平滑表面上或形成不連續性而進行標記。通過緩存每條邊兩側表面補丁的表面法線記錄，可以在存在大量基礎多邊形時非常高效地生成遮擋邊界和表面不連續性的可見性和位置。圖2展示了具有遮擋邊界的模型的示例。稍后，我們將描述模型表示如何有效地計算與每個參數相關的圖像特征的偏導數。

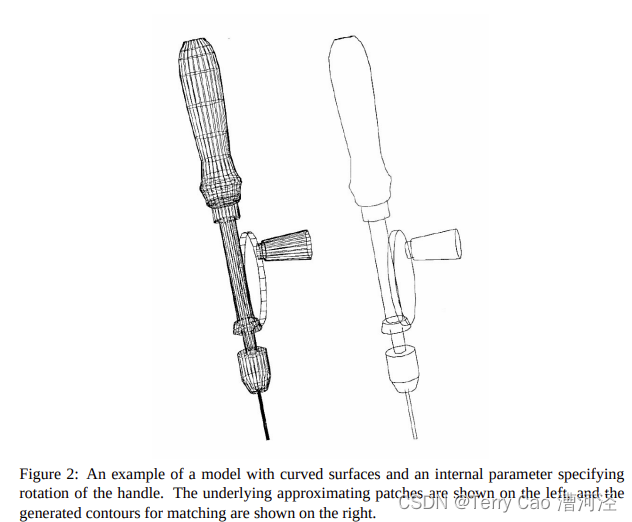
4 求解視點和模型參數

從3D到2D的投影是一種非線性操作。然而，幸運的是，它是一種平滑且行為良好的變換。投影前的深度旋轉將投影點轉換為旋轉角度余弦的函數。向攝像機方向的平移會引入作為距離倒數函數的透視畸變。平行于圖像平面的平移幾乎完全是線性的。與內部模型參數相關的平移和旋轉對模型點的影響與視點參數的效果相同，但僅應用于模型點的一個子集。所有這些變換都是平滑且行為良好的。因此，這個問題是應用牛頓法的有希望的候選者，該方法基于假設函數在局部是線性的。雖然這確實需要從未知參數的適當初始選擇開始，并面臨收斂到錯誤局部最小值的風險，但我們將在下面看到，穩定化方法可以使這種方法在實踐中非常有效。

4.1 牛頓法和最小二乘法優化

略

4.2 偏導數的高效計算

實現這種求解方法中最耗費資源的方面之一是計算偏導數的雅可比矩陣。因此，我們開發了一些方法，通過預計算和共享數據結構來降低這些成本。此外，還使用了一種特殊技術來處理關于完整三維旋轉的導數，以消除奇點并提高收斂速度。

如前述模型表示部分所述，所有模型點都是“框架”數據結構樹中的葉節點。每個框架表示相對于其父節點的旋轉或平移。因此，通過從每個模型點回溯到樹的根，可以確定影響該點的變量變換集。每個框架數據結構還包含當前視圖的預計算結果，所有依賴于該框架的點都可以使用這些結果來計算其相對于該框架參數的偏導數。由于通常有許多點受每個框架的影響，因此對框架結果的任何預計算都遠比為每個點分別計算它們更為高效。

在一條路徑上，同一個參數可能會出現在樹中的多個框架中（例如，人類手指的最后兩個關節不獨立運動，而是依賴于一個腱收縮參數）。這種情況可以通過簡單地對某個特定參數的所有偏導數求和來輕松處理。

每種類型的框架變換需要不同的預計算結果，因此這些將分別描述如下。

平移。每個可變平移框架包含一個三維向量，給出相對于該框架變量的方向導數。在所有依賴于該框架的點上，這個方向導數都是相同的，因此不需要進一步計算。

繞一個軸的旋轉。每個可變旋轉框架包含三維角速度向量和當前視點的旋轉原點。依賴于該框架的每個點的方向導數是通過將角速度向量與從旋轉原點到該點的向量取叉積來計算的。

繞三個軸的旋轉。如果我們通過依次繞各個軸的三次旋轉來計算任意三維旋轉，很容易出現奇點，這些奇點導致三次旋轉的組合未能指定獨立的旋轉方向。因此，我們用一個3x3的旋轉矩陣來表示完整的三自由度旋轉，并計算繞每個坐標軸的校正旋轉與此旋轉組合。這還有一個好處，即導數可以以極其高效的形式計算。例如，相對于繞x軸的增量旋轉，某點的方向導數是向量(0, z, -y)，其中z和y是從旋轉原點到該點的向量坐標。

一旦每個模型點的方向導數被計算出來，只需將這些導數投影到圖像坐標系(u, v)中。模型點(x, y, z)在攝像機坐標系中的透視投影產生圖像點(u, v)，如下所示：

其中，f是與攝像機鏡頭焦距成比例的常數。我們包含另一個常數a，指定原始圖像中每個像素的寬高比，因為大多數當前的視頻標準具有非正方形的寬高比。對上述函數中的每一個相對于參數p求偏導數，我們得到：

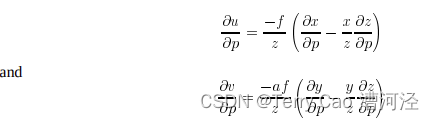
這里，x, y和z相對于p的偏導數就是之前計算的方向導數的分量。

4.3 測量曲線的垂直誤差

上述方法在模型點與圖像點之間存在匹配時是足夠的。然而，在大多數情況下，匹配實際上發生在模型的投影輪廓和圖像中的部分邊緣之間。由于圖像邊緣端點的精確位置未知（可能由于遮擋而移動），因此必須僅最小化圖像邊緣點到投影模型曲線的垂直距離。

可能認為自遮擋曲面的邊緣需要特殊處理，因為形成這種遮擋輪廓的實際模型邊緣會隨著視點的變化而移動。然而，在這種遮擋點處的表面法線正好與觀察方向垂直，因此投影到圖像中的輪廓的瞬時運動為零，因為表面上的鄰近點取代了它。對于較大的旋轉，通過補償其他非線性的相同迭代，可以輕松處理由非線性引入的誤差。

為了測量圖像點到投影二維模型線的垂直距離，將投影模型線表示為以下形式是有用的：

�sin?�?�cos?�=�usinθ?vcosθ=d

其中，�θ 是線相對于u軸的方向，d 是線到原點的有符號垂直距離。如果我們將圖像點 (�0,�0)(u0?,v0?) 代入此方程的左側并計算新的 �′d′，則該點到線的有符號垂直距離為 �′?�d′?d。這個垂直誤差測量的偏導數只是u和v偏導數的線性組合：

?�?�=sin?�?�?�?cos?�?�?�?p?d?=sinθ?p?u??cosθ?p?v?

在實際操作中，我們從線上的兩個點 (�1,�1)(u1?,v1?) 和 (�2,�2)(u2?,v2?) 計算 sin?�sinθ 和 cos?�cosθ。令L為這兩個點之間的線段長度：

�=(�2?�1)2+(�2?�1)2L=(u2??u1?)2+(v2??v1?)2?

則：

cos?�=�2?�1�cosθ=Lu2??u1?? sin?�=�2?�1�sinθ=Lv2??v1??

垂直誤差在圖像曲線上選定的點與此點垂直投影到投影模型曲線最近段之間進行測量。在每次迭代的過程中，這種最近匹配點的確定都會更新。

4.4 確定收斂的起始位置

Worrall、Baker 和 Sullivan [34] 使用蒙特卡洛技術研究了作者早期版本算法的收斂范圍。他們發現，對于旋轉誤差小于 90 度的情況，該算法幾乎在每一種情況下都能收斂到正確的解（平移誤差幾乎沒有影響）。迭代次數隨著誤差的增加而增加，最大在 90 度時平均約為 6 次迭代。結合下一節描述的穩定方法，收斂性能顯著提高。

因此，確定初始起始位置的精度要求相當低。對于作為我們初始重點的運動跟蹤問題，我們簡單地使用前一幀的參數估計，并為每個參數添加從前兩幀獲得的速度估計。對于一般的識別問題，可以使用與圖像匹配的屬性來確定初始參數估計。對于深度旋轉，每個匹配可以投票選擇一個平均方向（很少有模型特征從所有視點都可見），這些方向向量可以進行平均。對于圖像平面內的旋轉，我們可以從估計的深度旋轉投影模型，并取投影模型邊緣與匹配圖像邊緣之間的平均圖像旋轉。平移估計可以通過匹配投影模型特征和圖像特征的重心及重心的標準偏差來進行。有關識別問題初始估計的計算示例，請參見[21]。

如果只有大約與自由度數量相當的匹配點，則可能存在多個局部最小值。可以通過從一些額外匹配點開始（作者應用中采用的解決方案）、嘗試從多個起始位置收斂或使用應用于匹配子集的解析方法（如 Dhome 等人 [4]）計算候選起始位置集合來解決此問題。另一種方法是構建一個逆查找表，將特征測量映射到近似的視點參數估計。Thompson 和 Mundy [32] 對頂點使用了這種方法，Goad [7] 對廣泛的任意模型特征使用了這種方法。

5 穩定解決方案

只要對解的約束明顯多于未知數，前述的牛頓法通常會從廣泛的起始位置穩定收斂。然而，在識別和運動跟蹤問題中，通常希望從僅有的一些最可靠匹配開始，并使用這些匹配來縮小后續匹配的視點范圍。即使匹配點多于自由參數，通常也會出現一些匹配是平行的或具有其他關系，導致解的不適定。這些問題在模型具有許多內部參數時會進一步加劇。

5.1 指定先驗模型

所有這些問題都可以通過引入對期望解的先驗約束來解決，這些約束在沒有進一步數據時指定默認值。在許多情況下，默認解只是求解當前參數估計的零修正。然而，對于某些運動跟蹤問題，可以通過從速度和加速度測量中外推出特定的最終參數估計，這反過來意味著在非線性收斂的后續迭代中對參數值的非零偏好。

這些先驗約束中的任何一個都可以通過簡單地向線性系統添加行來包含，說明我們希望為每個參數分配的值：

[��]�=[��][JI?]x=[ed?]

單位矩陣 I 為每個參數指定一個值，��di? 指定參數 �i 的期望默認值。

這里明顯的問題是沒有指定滿足數據約束與滿足先驗模型約束之間的權衡。適當的解決方案是對矩陣方程的每一行進行加權，以使右側每個元素具有相同的標準偏差。因此，當我們最小化誤差向量時，每個約束將按其期望值的標準差數進行貢獻。

我們將系統的每一行歸一化為單位標準差。如果圖像測量以像素為單位，那么將其標準差保持為 1 是對測量圖像特征位置誤差的一個好的初步估計。在我們的匹配算法中，我們還考慮了匹配中的潛在模糊性，以增加標準差（即降低權重），對于表現出多個相鄰替代的匹配，以便正確匹配鄰近替代的模糊性轉化為適當的定位不確定性。

更重要的歸一化是根據每個參數的先驗估計標準差對先驗模型進行加權。這在運動跟蹤的情況下相對簡單，因為可以將每幀的加速度限制表示為標準差。然而，在從任意視點進行基于模型的識別的情況下，似乎預期值的范圍是無限的。事實上，在收斂期間每個參數都是有限的，因為我們假設從視點的一些初步近似開始。因此，旋轉參數的標準差最多為π/2，平移參數將限制在保持對象在圖像框架內。內部模型參數的標準差將對應于其有效運動范圍的較大部分。這些偏差可能比圖像測量產生的偏差大，但它們在穩定不適定問題的解中仍起著重要作用。事實上，標準差可以小幾倍而不會對最終解適合數據測量的程度產生不利影響，因為非線性迭代解可以將先驗模型的起點重置為每次迭代的結果。

5.2 穩定化的高效計算

參數值的先驗估計將通過對角矩陣 �W 進行加權，其中每個權重與參數 �i 的標準偏差 ��σi? 成反比：

���=1��Wii?=σi?1?

該矩陣用于對方程 (2) 的下部的每一行進行縮放。我們假設方程上部基于圖像測量的約束已經縮放為單位標準差。

[��]�=[���][JW?]x=[eWd?]

我們通過求解相應的正規方程來最小化這個系統：

(����)[��]�=(����)[���](JTWT)[JW?]x=(JTWT)[eWd?]

它展開為：

(���+���)�=���+����(JTJ+WTW)x=JTe+WTWd

由于 �W 是一個對角矩陣，���WTW 也是一個對角矩陣，但對角線上的每個元素是標準偏差的平方的倒數。這意味著穩定化的計算成本是微不足道的，因為我們可以首先形成 ���JTJ，然后簡單地在對角線上添加一些小常數，這些常數是每個參數的標準偏差的平方的倒數。如果 �d 非零，則將這些常數乘以 �d 添加到右側。如果原系統中的行數少于參數數目，我們可以簡單地添加足夠的零行以形成方陣，并將常數添加到對角線上以穩定它。

5.3 強制收斂

即使在基于先驗模型進行這種穩定化之后，系統仍可能由于線性近似于非線性系統而無法收斂到最小值。我們可以通過添加一個標量參數 λ 來強制收斂，該參數可以在發生發散時增加穩定化的權重。該系統的新形式為：

[JλW?]x=[eλWd?]

該系統最小化以下公式：

∥Jx?e∥2+λ2∥W(x?d)∥2

視覺領域的許多人會認識到這是一種使用 Tikhonov [33] 穩定泛函進行正則化的例子，該方法已應用于許多低級視覺領域（Poggio 等 [28]）。在這種情況下，參數 �λ 控制近似新數據 ∥��?�∥2∥Jx?e∥2 與最小化解與其原始起始位置 �d 之間距離 ∥�(�?�)∥2∥W(x?d)∥2 的權衡。

這種強制迭代收斂參數 �λ 的使用最早由 Levenberg [17] 研究，后來由 Marquardt [24] 歸結為具體的數值程序。他們意識到，隨著參數 �λ 的增加，解將越來越對應于步長越來越小的純梯度下降，并具有保證（但緩慢）的收斂性。對于減少的 �λ，問題則轉向牛頓法，它在解附近具有快速的二次收斂，但在起始位置太遠時可能會發散。因此，Marquardt 建議簡單的解決方案是監控每個解的殘差，并將 �λ 增加 10 倍直到殘差減少；否則，在每次迭代時將 �λ 減少 10 倍。這并不能保證任何特定的收斂率，當然也可能收斂到局部而非全局最小值。然而，它在實踐中證明是非常有效的，是非線性最小二乘問題中最廣泛使用的方法之一。

Marquardt 并沒有假設對加權矩陣 �W 的任何先驗知識，而是從 ���JTJ 的相應列的歐幾里德范數估計其每個元素。在我們的情況下，�W 的可用性使得當 ���JTJ 的某列接近零時，算法可以表現得更好。它還使得穩定化具有更可預測的行為。增加 �λ 的值將基本凍結具有最低標準偏差的參數，從而首先求解具有較高標準偏差的參數。對于我們的問題，這意味著對于困難的問題，收斂將首先通過求解平移，然后在后續迭代中求解旋轉，最后求解短程內部模型參數。

6 實現結果

前述所有的物體建模和參數求解方法均已用約4000行的C代碼實現。圖3展示了一個非常簡單的模型擬合示例。該模型是一個具有可變高度的金字塔。模型從一組特定的參數值投影出來，并隨機選擇了一些投影段的間隔進行匹配。改變模型參數以生成圖3(b)所示的起始參數估計。在此圖中，正交誤差以灰色條顯示在投影的模型段和匹配的圖像段之間。圖3(c)和圖3(d)展示了上述穩定算法在前兩次迭代后的輸出。在大范圍的初始參數值內，這種快速的收斂率通常在幾次迭代內即可實現（旋轉參數誤差高達60度）。關于在添加穩定化和Levenberg-Marquardt方法之前在廣泛誤差范圍內的收斂系統探索，可參見Worrall、Baker和Sullivan的研究[34]。事實上，發散的情況相對罕見，因此Levenberg-Marquardt方法很少生效；但其計算成本也較低，因此可能具有實用價值。

6.1 應用于運動跟蹤

這些方法的初始應用之一是基于模型的運動跟蹤問題。使用Datacube圖像處理器在512 x 485像素圖像上實時實現Marr-Hildreth[25]邊緣檢測。包含這些邊緣點的圖像被傳送到Sun 3/260上，在該處基于局部連通性將邊緣鏈接成列表。一個相當簡單的匹配技術用于識別最接近當前3-D模型投影輪廓的圖像邊緣。使用最好的初始匹配執行一次視點解算，然后從新的視點估計中生成進一步的匹配。此過程最多進行5次迭代，逐漸縮小搜索潛在匹配的圖像位置范圍（這有助于消除任何錯誤的外部匹配）。對于具有直邊的簡單模型，所有這些步驟可以在不到1秒的時間內完成，結果是一個可以執行穩健但相當慢的實時運動跟蹤系統。我們已經在視頻攝像機前緩慢移動物體的情況下連續運行了數千幀。通過觀察當前參數估計集上疊加的線框模型，可以實時輕松判斷運動跟蹤的正確性。目前我們正在探索使用并行架構來大大加快該系統的操作速度，以便在復雜物體模型的情況下達到視頻速率。圖4-7展示了該系統在某一幀運動跟蹤中的操作情況。然而，由于模型的復雜性，該版本在Sun 3/260上每幀需要約6秒的處理時間，無法實時運行。圖4展示了一個手電鉆的圖像，其中邊緣是用簡化版的Canny邊緣檢測器提取的。圖5中，模型疊加在這些邊緣上，顯示了先前最佳估計的當前視點。一個簡單的匹配算法用于找到接近投影模型曲線的圖像邊緣，并覆蓋最大可能長度的邊緣。這些匹配根據其長度和平均分離度進行排名，并選擇最好的進行最小化。圖5中用粗線顯示了選擇的匹配，以及標記模型和圖像曲線之間誤差的正交條。模型擬合一次迭代后，圖6顯示了新模型位置及從該位置生成的新圖像匹配集。注意，手柄的旋轉是一個自由參數以及視點參數。第二次收斂迭代后的最終模型擬合結果如圖7所示，疊加在原始圖像上。盡管由于遮擋和低級邊緣檢測中的誤差，最終結果僅基于預測圖像邊緣的一小部分。然而，由于問題的過度約束性質，即可用測量值遠多于未知參數，最終結果可以是可靠且準確的。

7 結論與未來方向

本文提出了將具有任意曲面和任意數量內部參數的模型與匹配的圖像特征擬合的一般方法。對于穩健性和效率問題給予了相當大的關注，這些技術應能作為基于模型的視覺應用中模型擬合的實用基礎。

有多個方向可以進一步改進這些方法。其一是處理具有大量可變參數的物體。由于求解線性系統的復雜性隨變量數量的增加而呈O(n^3)增長，因此將具有大量參數的問題劃分為較小的子集可能更為高效。對于不確定性范圍大的所有參數使用同時求解方法，但剩余參數則基于局部獨立優化求解。如果建模的是通用類別的物體，如Acronym系統[3]中幾乎每個維度都可變的物體，這將變得尤為重要。

雖然本文擴展了視覺系統的建模和參數求解組件，使其能夠處理曲面物體，但在低級別曲線分割和分組方面仍有許多研究工作需要完成。作者已經開發了一些適合初始曲線描述的多尺度曲線平滑方法[23]，但在分組和索引方面仍有大量工作要做，以實現曲面物體識別的完全通用系統。通過利用諸如曲率、平滑性和高級分組等特性，應該可以在匹配的可靠性方面取得重大進展。