2024-5-23,星期四,22:20,天氣:晴,心情:晴。今天沒有什么重要的事情發生,心情一如既往的平靜,距離返校假期還有兩天~~~。
今天觀看了石群老師電路基礎課程的第23/24個視頻,開始了一階、二階電路的學習,主要學習內容為:動態電路、動態電路方程的推導(RC、RL、RLC、高階電路)、電路的初始條件及例題;C語言方面開啟了第六章的學習,并繼續完善總結C語言學習筆記。
1. 動態電路
含有動態元件電容和電感的電路稱動態電路。當動態電路狀態發生改變時(換路)需要經歷一個變化過程才能達到新的穩定狀態。這個變化過程稱為電路的過渡過程。從下面一電阻電路可以看出,在非動態電路中,這一過渡期為零。
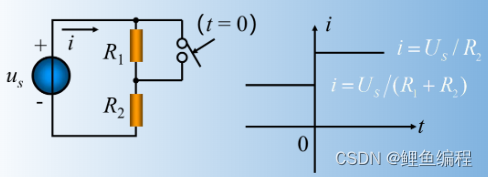
但從下面含電容的電路中可以看出,動態電路存在一明顯過渡期(電感電路類似)。
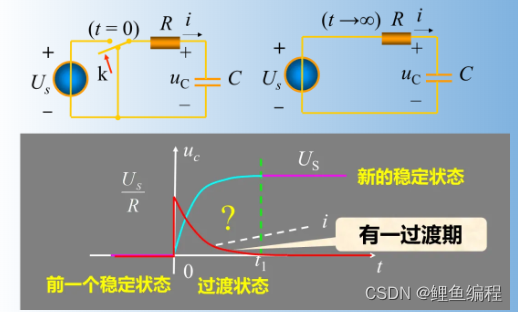
工程實際中在切斷電容或電感電路時會出現過電壓和過電流現象。
換路:
電路結構、狀態發生變化,包括支路的連接和斷開,電路參數的變化。
過渡過程產生的原因:
電路內部含有儲能元件L、C,電路在換路時能量發生變化,而能量的儲存和釋放都需要一定的時間來完成。

2.?動態電路的方程
RC電路方程推導:
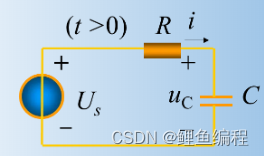

RL電路方程推導:?
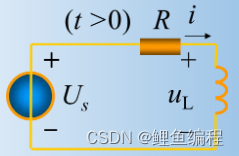

綜上,含有一個動態元件電容或電感的線性電路,其電路方程為一階線性常微分方程,稱一階電路。

RLC電路方程推導:?
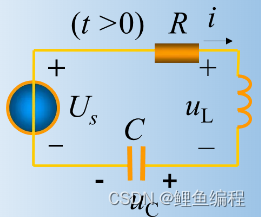
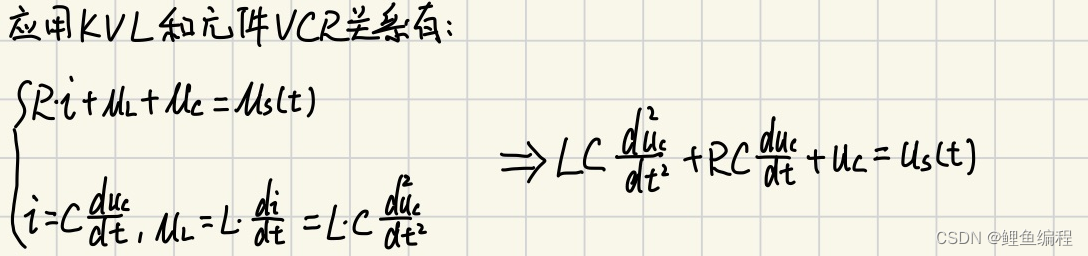
含有二個動態元件的線性電路,其電路方程為二階線性常微分方程,稱二階電路。
綜合上述分析可以看出:描述動態電路的電路方程為微分方程;動態電路方程的階數通常等于電路中動態元件的個數。
(a)一階電路:一階電路中只有一個動態元件,描述電路的方程是一階線性微分方程。
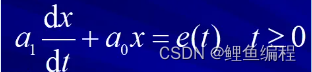
(b)二階電路:二階電路中有二個動態元件,描述電路的方程是二階線性微分方程。
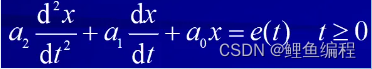
(c)高階電路:電路中有多個動態元件,描述電路的方程是高階微分方程。?
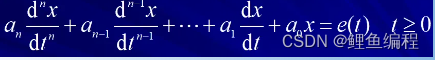
電路的穩態分析與動態分析:
(a)穩態分析包括:恒定或周期性激勵;換路發生很長時間后狀態;微分方程的特解。
(b)動態分析包括:任意激勵;換路發生后的整個過程;微分方程的通解。
3. 電路的初始條件
電容的初始條件推導:
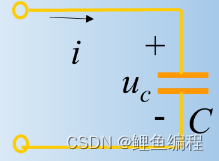
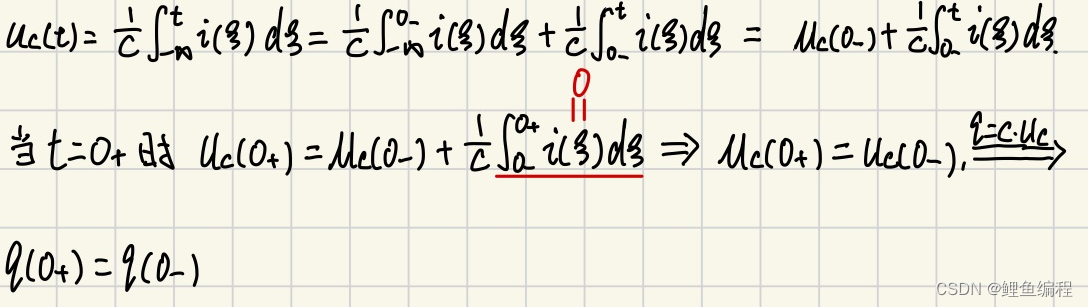
綜上可知,換路瞬間,若電容電流保持為有限值, 則電容電壓(電荷)換路前后保持不變。
電感的初始條件推導:
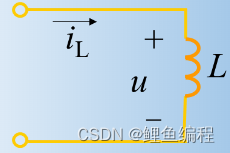
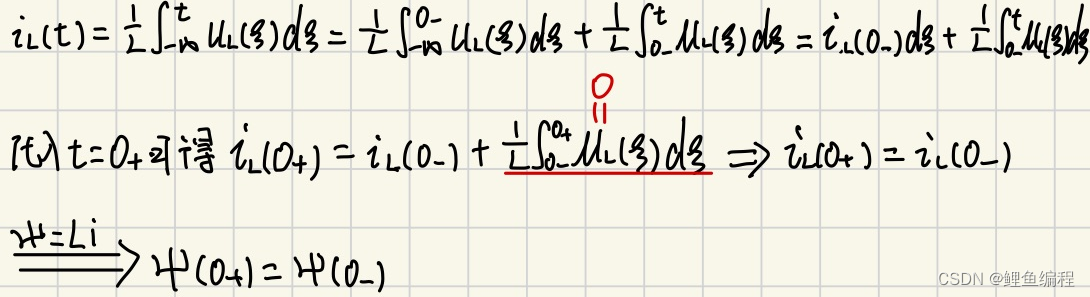
綜上可知,換路瞬間,若電感電壓保持為有限值, 則電感電流(磁鏈)換路前后保持不變。
電路初始值的確認:
(1)由換路前電路(穩定狀態)求uC(0-)和iL(0-)
(2)由換路定律得uC(0+) 和 iL(0+)
(3)畫0+等效電路:電容用電壓源替代(無電壓相當于導線);電感用電流源替代(無電流相當于開路),方向與原假定方向相同
(4)由0+電路求所需各變量的0+值。
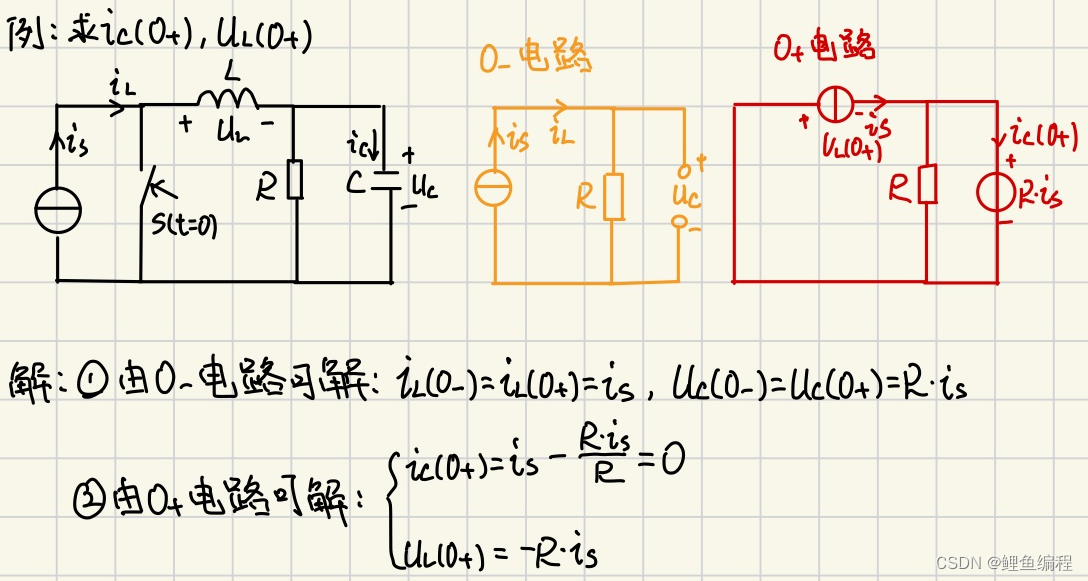
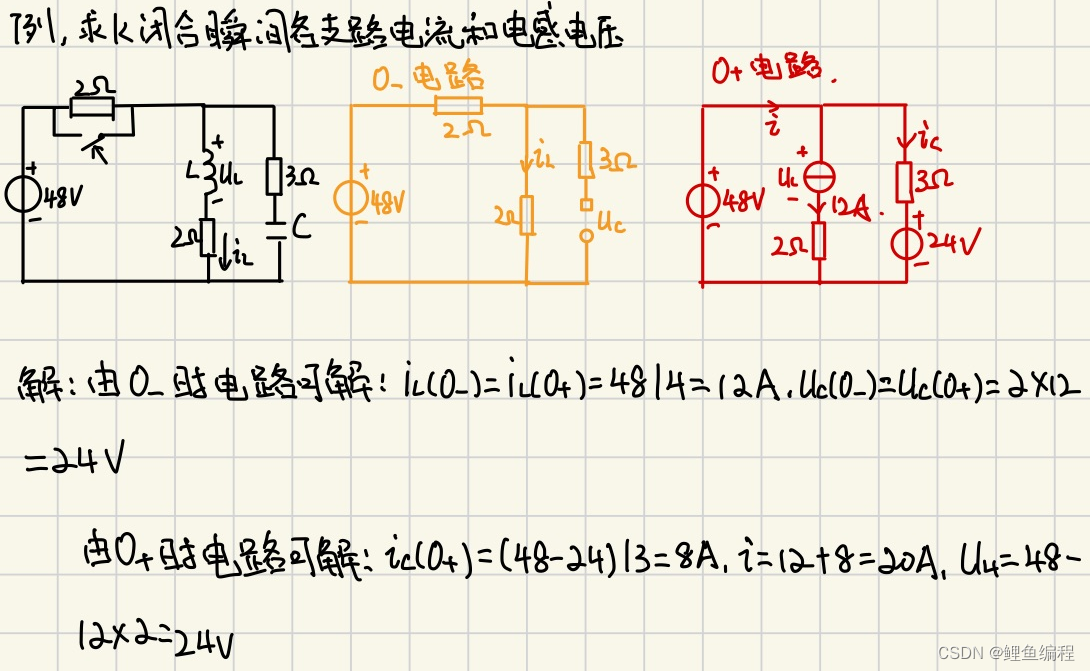
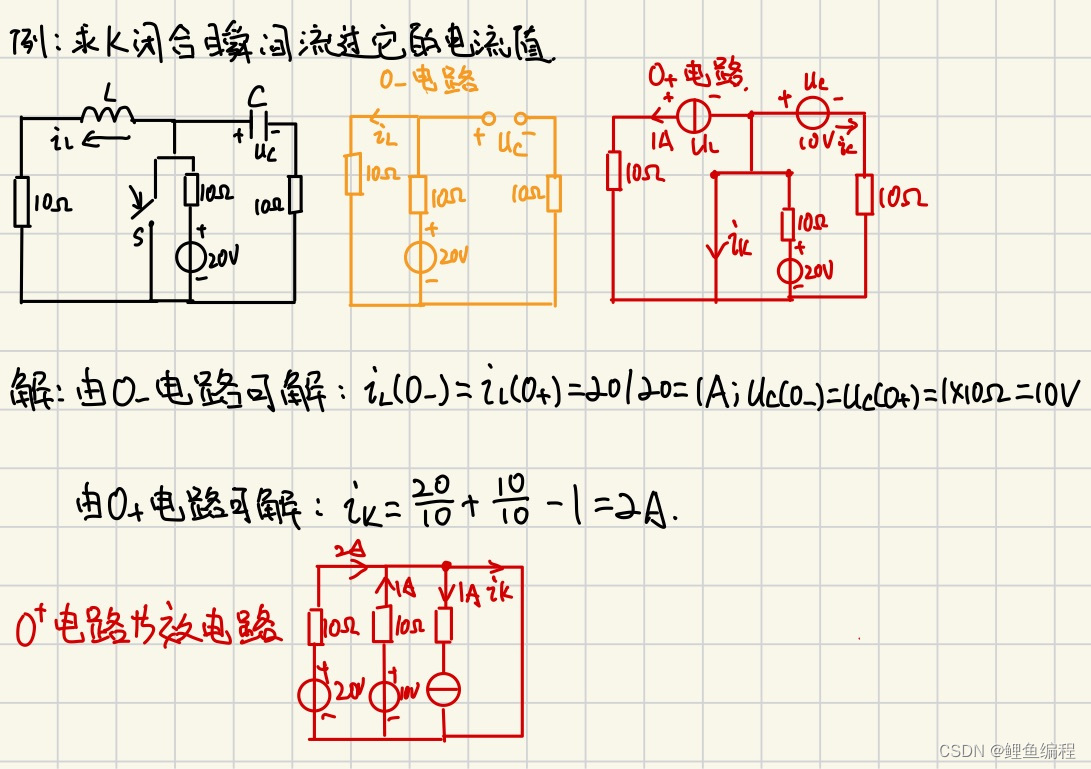
?今日總學習時長約4h30min,明日學習內容為:電路基礎的第25、26個視頻內容;C語言第六章(第七章)內容。


)



】)









函數使用,C中“—>” 和“ . ” 作用與區別)



