目錄

一、求所有結點個數

1.1 遞歸思路

1.2 遞歸分支圖

1.3 遞歸棧幀圖

1.4 C語言實現

二、求葉子結點個數

2.1 遞歸思路

2.2 遞歸分支圖

2.3 遞歸棧幀圖

2.4 C語言實現

三、求第K層的結點個數

3.1 遞歸思路

3.2 遞歸分支圖

3.3 遞歸棧幀圖

3.4 C語言實現

四、求二叉樹高度

4.1 遞歸思路

4.2 遞歸分支圖

4.3 遞歸棧幀圖

4.4 注意事項

4.5?C語言實現

---

一、求所有結點個數

1.1 遞歸思路

考慮特殊情況：

1. 如果是空節點，返回0

考慮一般情況：

1. 總結點的數目就是左右子樹所含結點的和加上自身結點

2. 每個節點都可被看作根節點，去重復遞歸左右子樹

1.2 遞歸分支圖

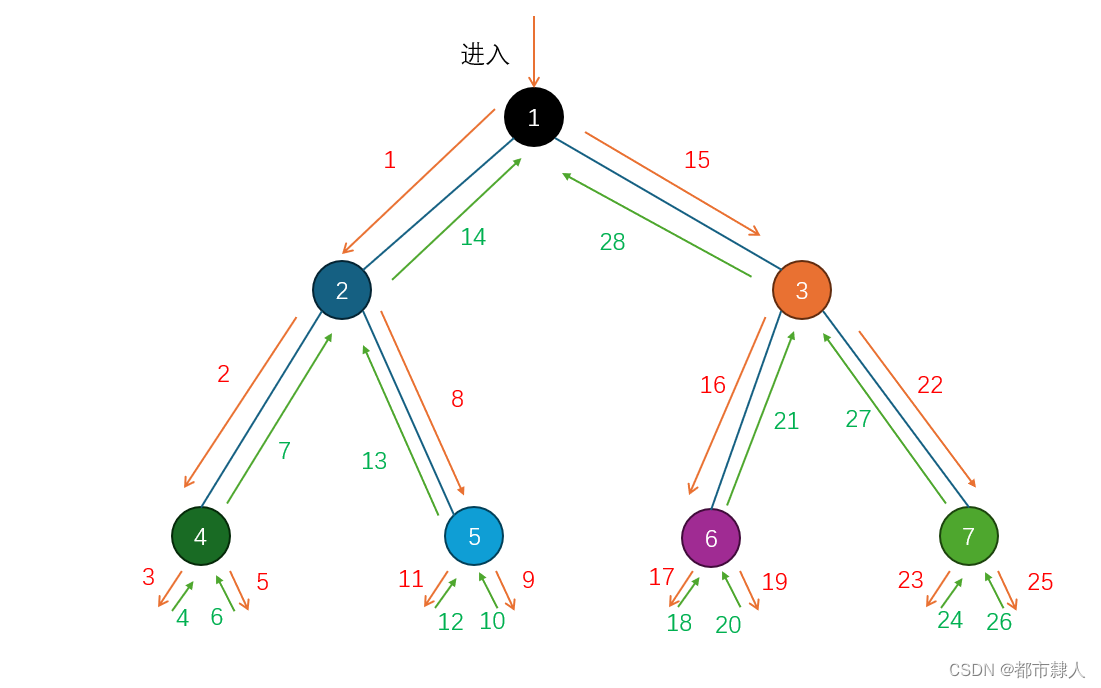
1.3 遞歸棧幀圖

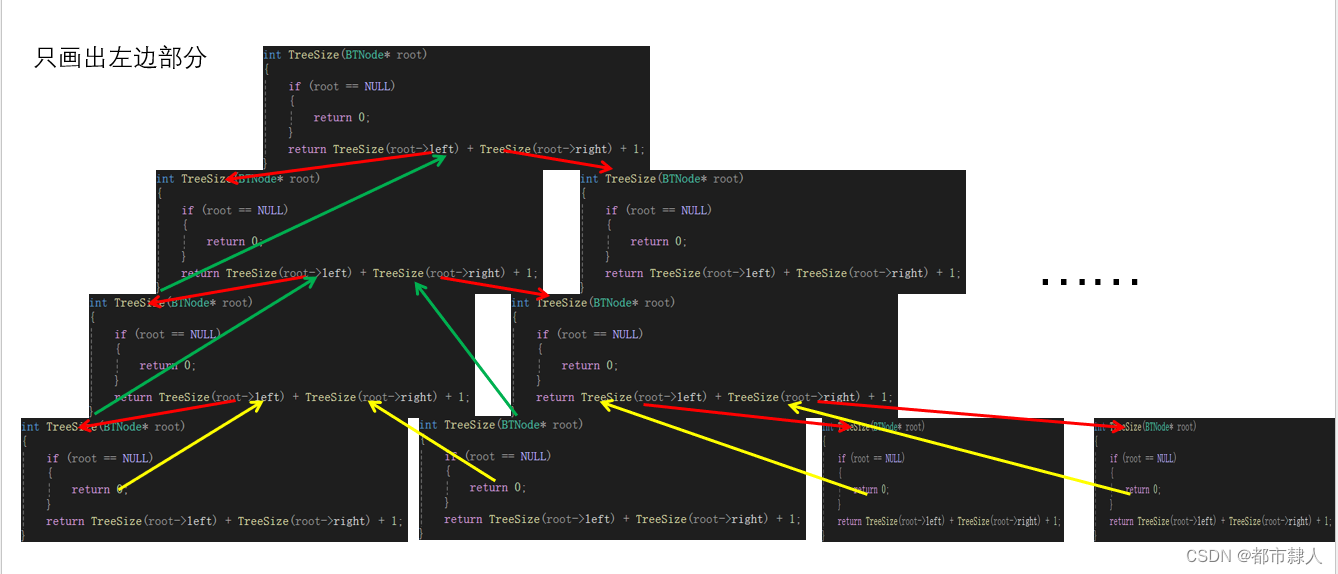
1.4 C語言實現

int TreeSize(BTNode* root)
{if (root == NULL){return 0;}return TreeSize(root->left) + TreeSize(root->right) + 1;
}

二、求葉子結點個數

2.1 遞歸思路

考慮特殊情況：

1. 如果是空節點，則返回0
2. 如果是葉子結點，則返回1

考慮一般情況：

1. 總結點的數目就是左右子樹所含結點的和

2. 每個節點都可被看作根節點，去重復遞歸左右子樹

2.2 遞歸分支圖

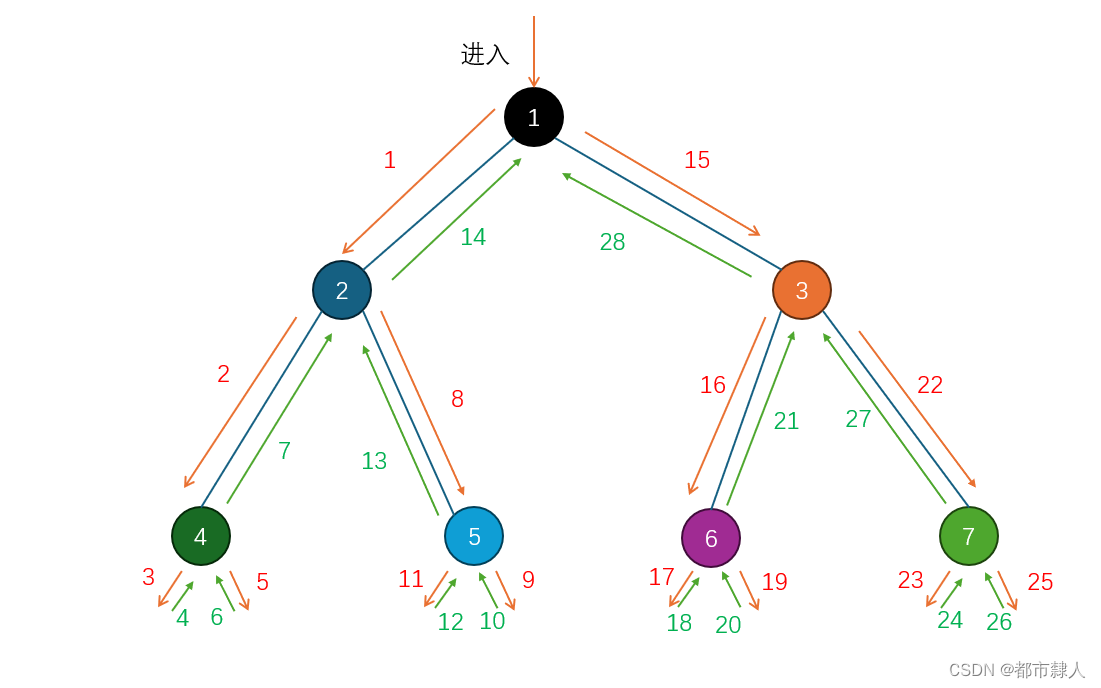
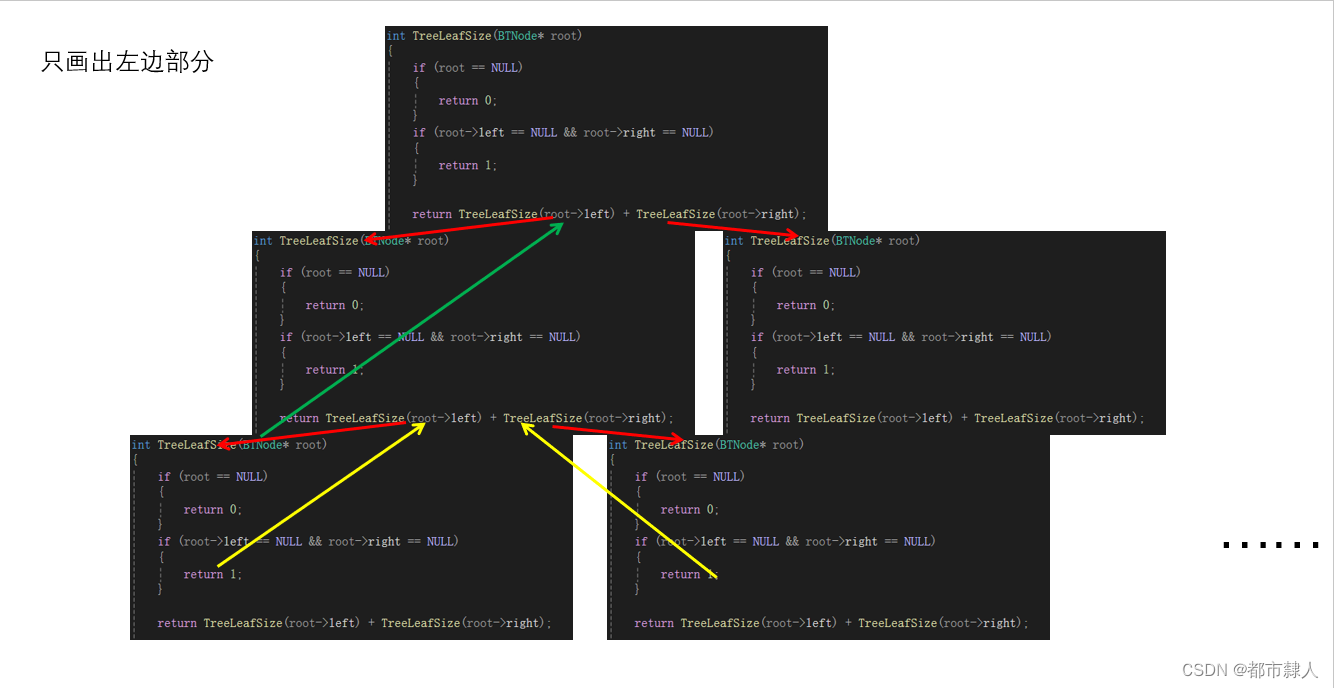
2.3 遞歸棧幀圖

?

2.4 C語言實現

int TreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);}

三、求第K層的結點個數

3.1 遞歸思路

考慮特殊情況：

1. 如果結點為空，返回0
2. 如果層數為1，返回1

考慮一般情況：

每個節點都可被看作根節點，去重復遞歸左右子樹。那么此時層數要減去1

3.2 遞歸分支圖

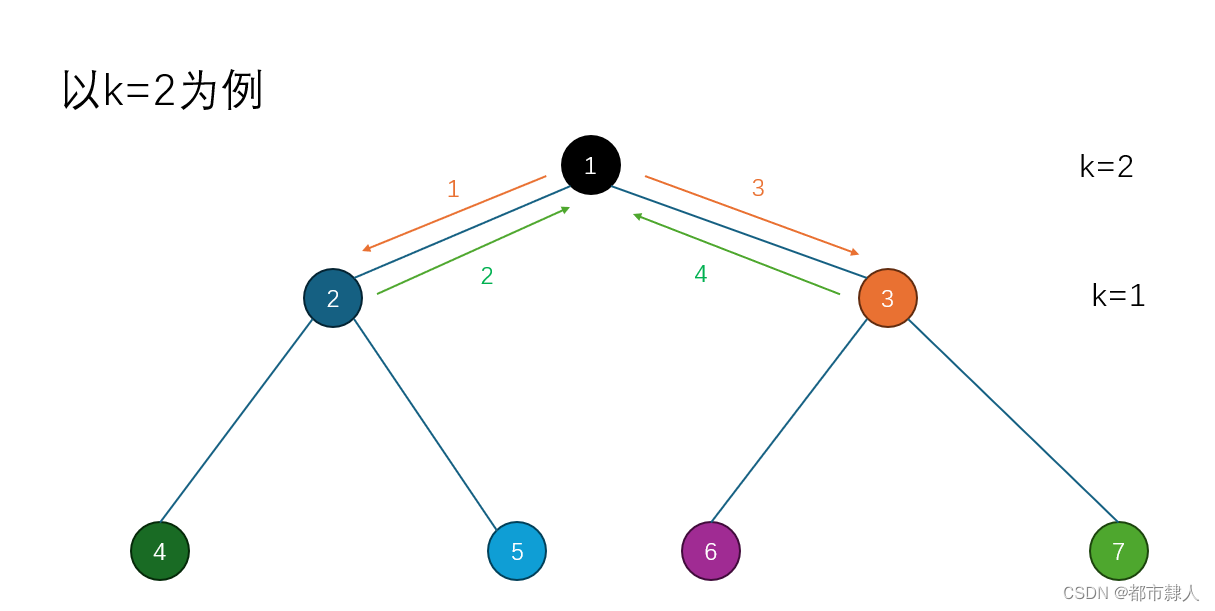
3.3 遞歸棧幀圖

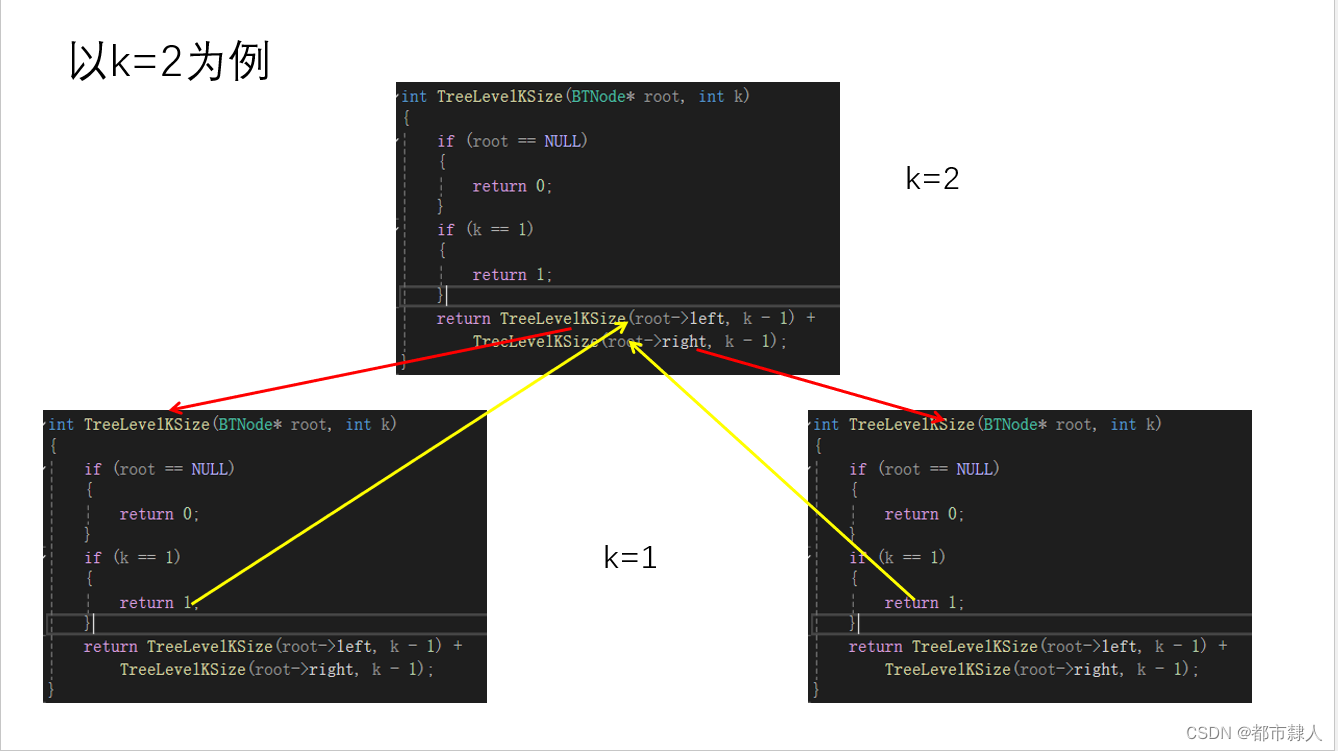
3.4 C語言實現

int TreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return TreeLevelKSize(root->left, k - 1) + TreeLevelKSize(root->right, k - 1);
}

四、求二叉樹高度

4.1 遞歸思路

考慮特殊情況：

1. 如果結點為空，返回0

考慮一般情況：

1. 高度就等于子樹的高度加上自身的高度
2. 返回的是左右子樹中更大的值

4.2 遞歸分支圖

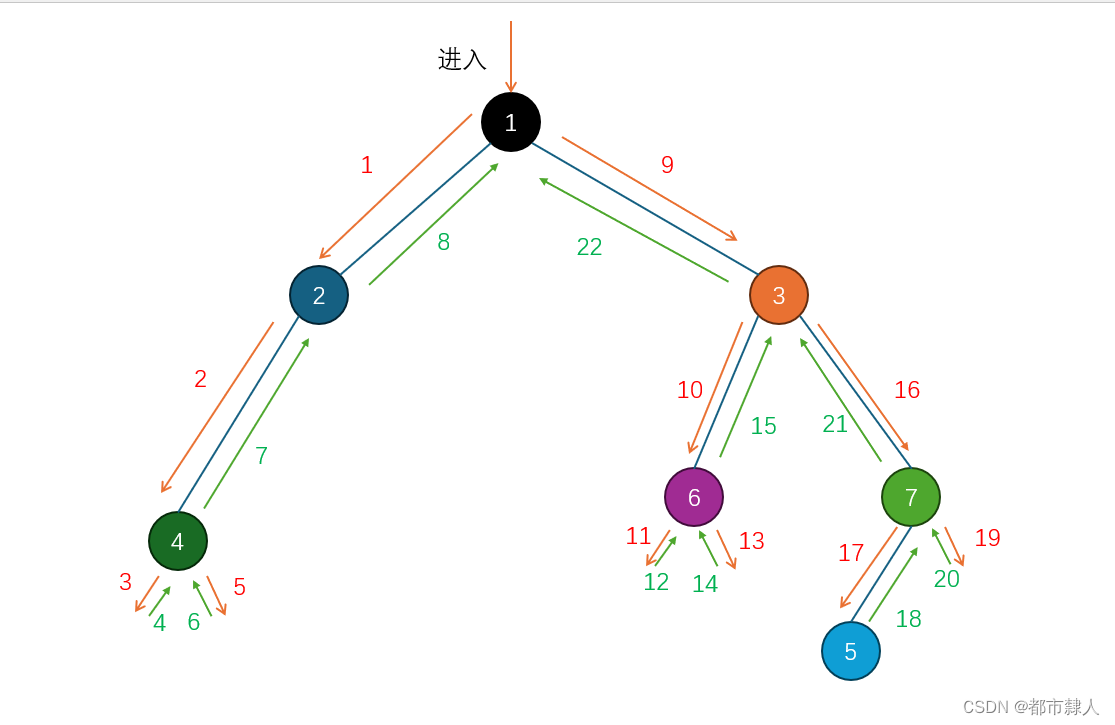
4.3 遞歸棧幀圖

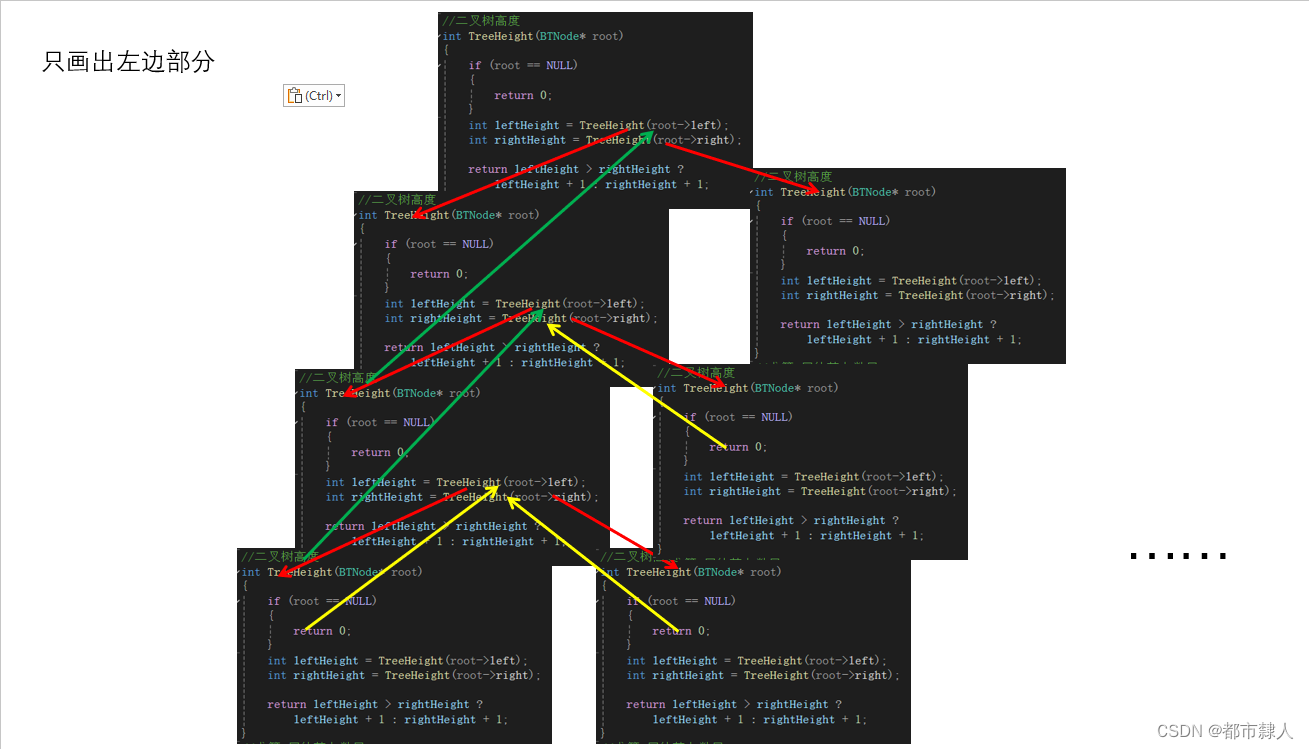
4.4 注意事項

由遞歸的知識可知，函數每次調用都會建立棧幀，各個棧幀間互不影響，所以需要把每次得到的值存起來，不然每次調用都會去再次遞歸尋找。大大浪費時間，降低程序執行的效率。

4.5?C語言實現

int TreeHeight(BTNode* root)
{if (root == NULL){return 0;}int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ?leftHeight + 1 : rightHeight + 1;
}