概述
本案例是基于之前的嶺回歸的案例的。之前案例的完整代碼如下:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge, LinearRegression
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_diabetes
from sklearn.model_selection import learning_curve, KFolddef plot_learning_curve(est, X, y):# 將數據拆分20次用來對模型進行評分training_set_size, train_scores, test_scores = learning_curve(est,X,y,train_sizes=np.linspace(.1, 1, 20),cv=KFold(20, shuffle=True, random_state=1))# 獲取模型名稱estimator_name = est.__class__.__name__# 繪制模型評分line = plt.plot(training_set_size, train_scores.mean(axis=1), "--", label="training " + estimator_name)plt.plot(training_set_size, test_scores.mean(axis=1), "-", label="test " + estimator_name, c=line[0].get_color())plt.xlabel("Training set size")plt.ylabel("Score")plt.ylim(0, 1.1)# 加載數據
data = load_diabetes()
X, y = data.data, data.target# 繪制圖形
plot_learning_curve(Ridge(alpha=1), X, y)
plot_learning_curve(LinearRegression(), X, y)
plt.legend(loc=(0, 1.05), ncol=2, fontsize=11)
plt.show()
輸出結果如下:

套索回歸的基本用法
引入套索回歸,還是基于糖尿病數據,進行模型的訓練。
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_diabetes
import numpy as np# 加載數據
data = load_diabetes()
X, y = data.data, data.target# 切割數據
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=8)# 使用套索回歸擬合數據
reg = Lasso().fit(X_train, y_train)# 查看結果
print(reg.score(X_train, y_train))
print(reg.score(X_test, y_test))
print(np.sum(reg.coef_ != 0))
輸出結果如下:
0.3624222204154225
0.36561940472905163
3
調整套索回歸的參數
上面的案例中,評分只有0.3,很低,我們可以試試調低alpha的值試試。
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_diabetes
import numpy as np# 加載數據
data = load_diabetes()
X, y = data.data, data.target# 切割數據
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=8)# 使用套索回歸擬合數據
reg = Lasso(alpha=0.1, max_iter=100000).fit(X_train, y_train)# 查看結果
print(reg.score(X_train, y_train))
print(reg.score(X_test, y_test))
print(np.sum(reg.coef_ != 0))
輸出如下:
0.5194790915052719
0.4799480078849704
7
可以發現,評分有所增長,10個特征中,這里用到了7個特征。
過擬合問題
如果我們把alpha的值設置得太低,就相當于把正則化的效果去除了,模型就會出現過擬合問題。
比如,我們將alpha設置為0.0001:
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_diabetes
import numpy as np# 加載數據
data = load_diabetes()
X, y = data.data, data.target# 切割數據
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=8)# 使用套索回歸擬合數據
reg = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train)# 查看結果
print(reg.score(X_train, y_train))
print(reg.score(X_test, y_test))
print(np.sum(reg.coef_ != 0))
輸出如下:
0.5303797950529495
0.4594491492143349
10
從結果來看,我們用到了全部特征,而且模型在測試集上的分數要稍微低于alpha等于0.1的時候的得分,說明降低alpha的數值會讓模型傾向于出現過擬合的現象。
套索回歸和嶺回歸的對比
我們采用圖像的形式,來對比不同alpha的值的時候,套索回歸和嶺回歸的系數。
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_diabetes
import numpy as np# 加載數據
data = load_diabetes()
X, y = data.data, data.target# 切割數據
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=8)# 使用套索回歸擬合數據并繪圖
reg = Lasso(alpha=1, max_iter=100000).fit(X_train, y_train)
plt.plot(reg.coef_, "s", label="Lasso alphat=1")reg = Lasso(alpha=0.11, max_iter=100000).fit(X_train, y_train)
plt.plot(reg.coef_, "^", label="Lasso alphat=0.11")reg = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train)
plt.plot(reg.coef_, "v", label="Lasso alphat=0.0001")reg = Lasso(alpha=0.1, max_iter=100000).fit(X_train, y_train)
plt.plot(reg.coef_, "o", label="Lasso alphat=0.1")plt.legend(ncol=2,loc=(0,1.05))
plt.ylim(-25,25)
plt.xlabel("Coefficient index")
plt.show()
輸出:
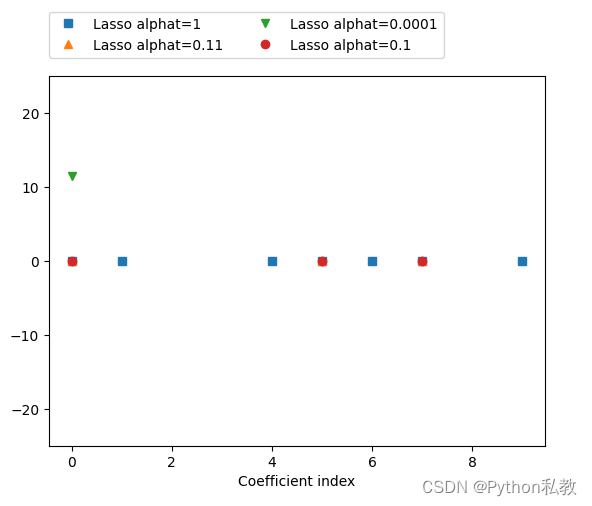






)



)





)


![[Linux] 常用服務器命令(持續更新)](http://pic.xiahunao.cn/[Linux] 常用服務器命令(持續更新))