論文地址：https://arxiv.org/abs/1709.04875

Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting

一、摘要

準時準確的交通預測對城市交通控制和引導至關重要。由于交通流的高非線性和復雜性，傳統方法無法滿足中長期預測任務的要求，并且通常忽視空間和時間依賴關系。本文提出了一種新穎的深度學習框架，即時空圖卷積網絡（STGCN），用于解決交通領域的時間序列預測問題。我們不是應用常規的卷積和循環單元，而是在圖上制定問題，并利用完整的卷積結構構建模型，這使得訓練速度更快，參數更少。實驗證明，我們的模型STGCN通過建模多尺度交通網絡有效地捕獲了全面的時空相關性，并在各種真實世界的交通數據集上始終優于最先進的基線模型。

二、數據集介紹

美國洛杉磯交通數據集 METR-LA 介紹

T-GCN文章選取了該數據集2012年3月1日至3月7日期間的207個傳感器及其交通速度。每5分鐘匯總一次交通速度。**相似性，數據總結出一個鄰接矩陣和一個特征矩陣。鄰接矩陣是由交通網絡中傳感器之間的距離計算出來的。**由于Los-loop數據集包含一些缺失的數據，使用線性插值法來填補缺失值.

SOTA算法：

https://paperswithcode.com/sota/traffic-prediction-on-metr-la

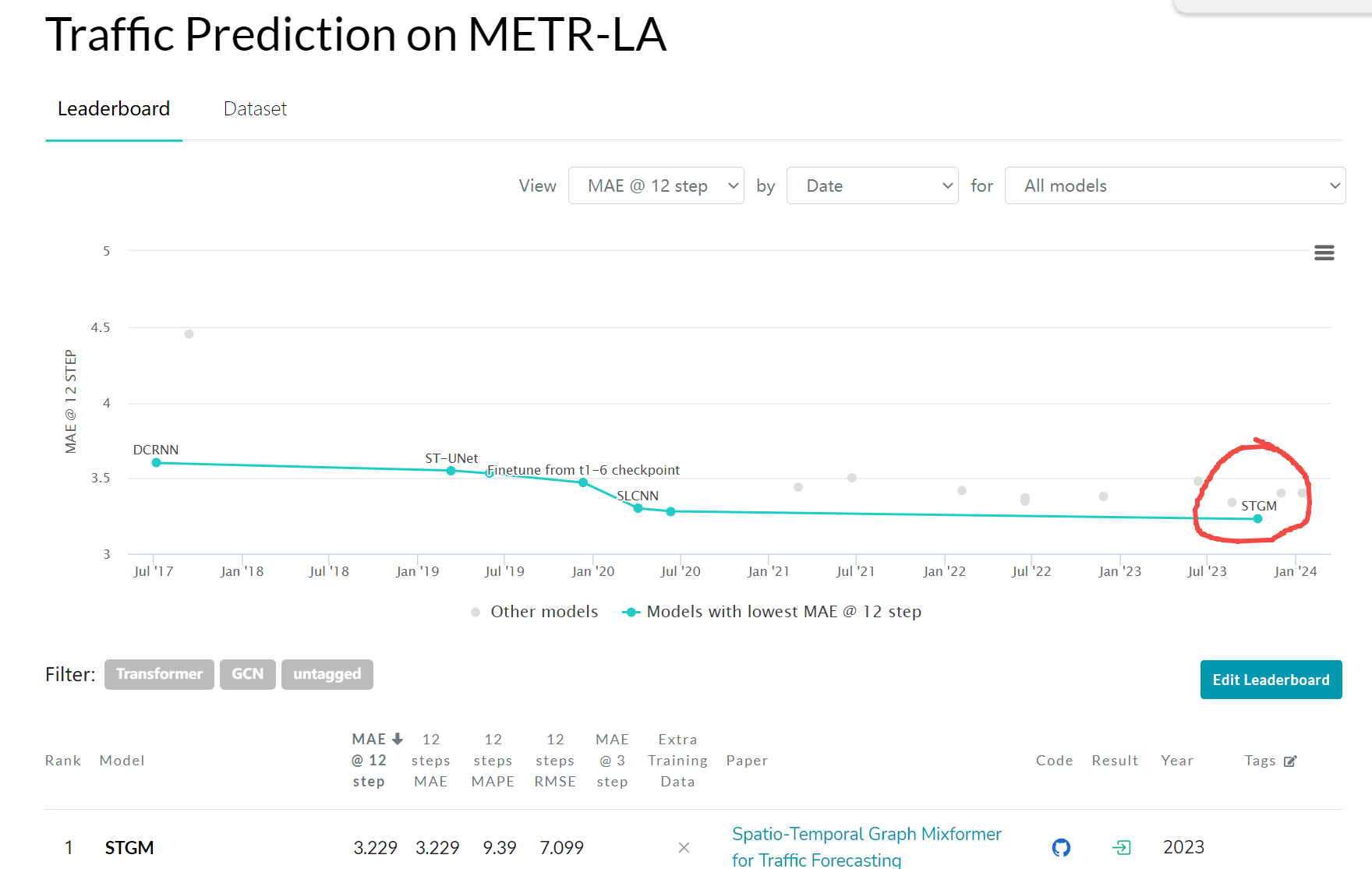
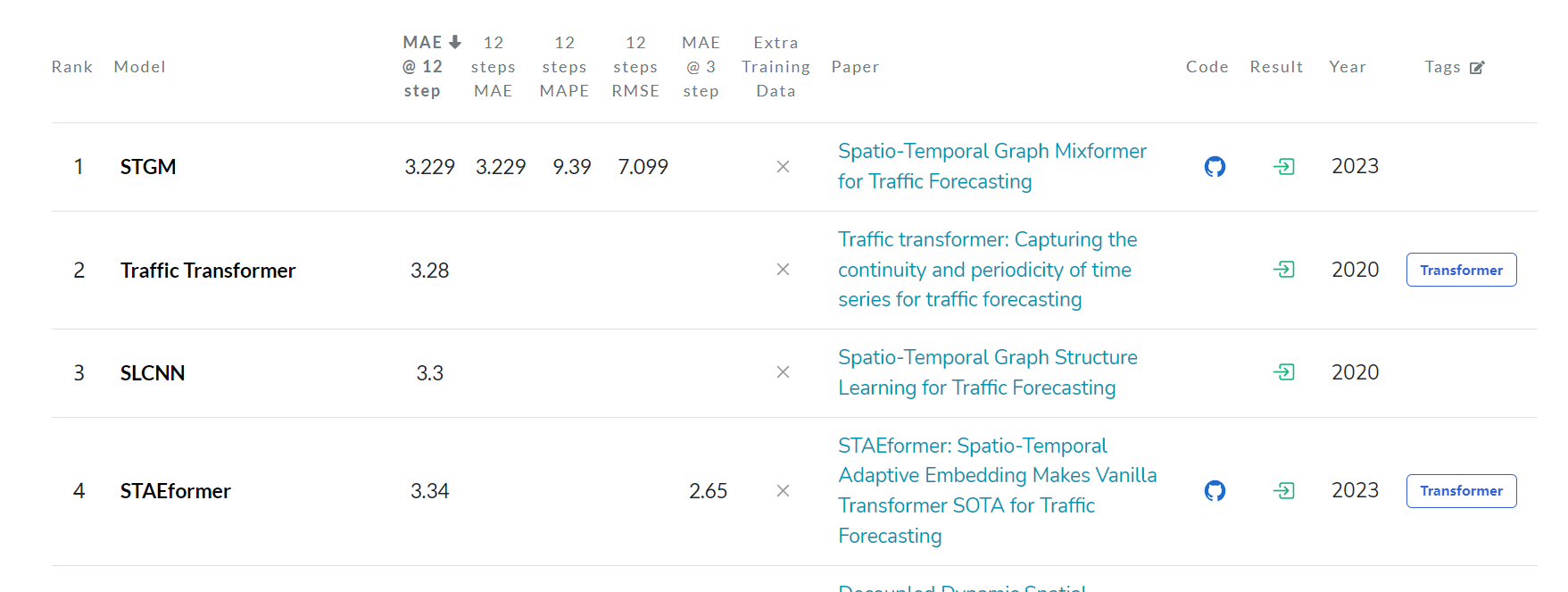
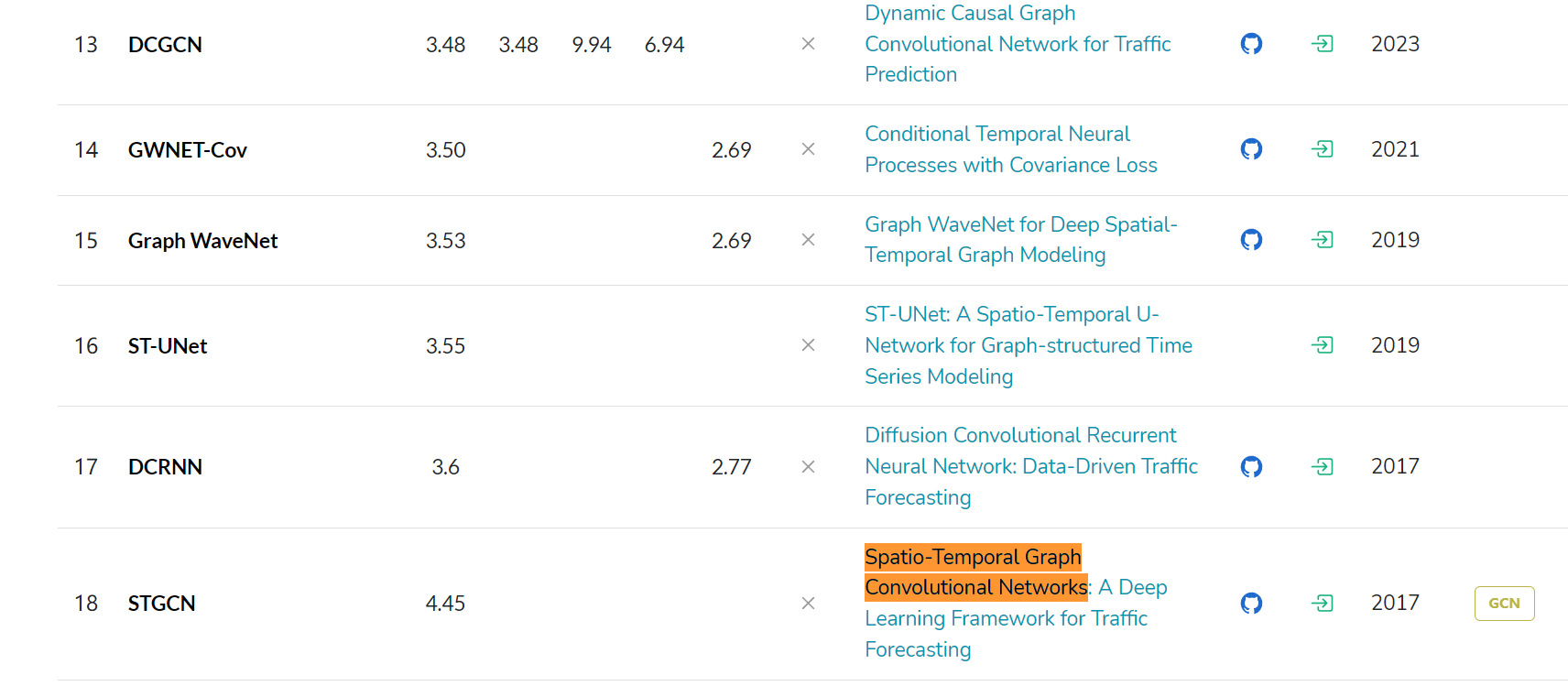
目前第一名是Spatio-Temporal Graph Mixformer for Traffic Forecasting，而本文的STGCN只能排18。

美國加利福尼亞交通數據集 PEMS-BAY 介紹

PEMS-BAY 數據集由加利福尼亞大學伯克利分校的交通實驗室發布。該數據集包含了舊金山灣區高速公路網絡上 325 個傳感器的實時交通流量數據。這個數據幫助對基于多源數據的交通預測算法進行評估和比較，并被廣泛用于交通預測、擁堵控制、出行決策等領域的研究中。

SOTA:

https://paperswithcode.com/sota/traffic-prediction-on-pems-bay

美國加利福尼亞交通數據集 PEMSD7-M 介紹

SOTA:
https://paperswithcode.com/sota/traffic-prediction-on-pemsd7-m

PEMSD7-M 數據集由美國加州大學洛杉磯分校的智能交通系統實驗室發布。該數據集收集了洛杉磯城市高速公路上的交通流量數據，包含了 228 個傳感器（探頭）每 5 分鐘采樣一次的方式收集數據。這個數據集旨在幫助進行基于不同時間尺度的交通預測研究，以提高道路網絡可持續性和安全性。

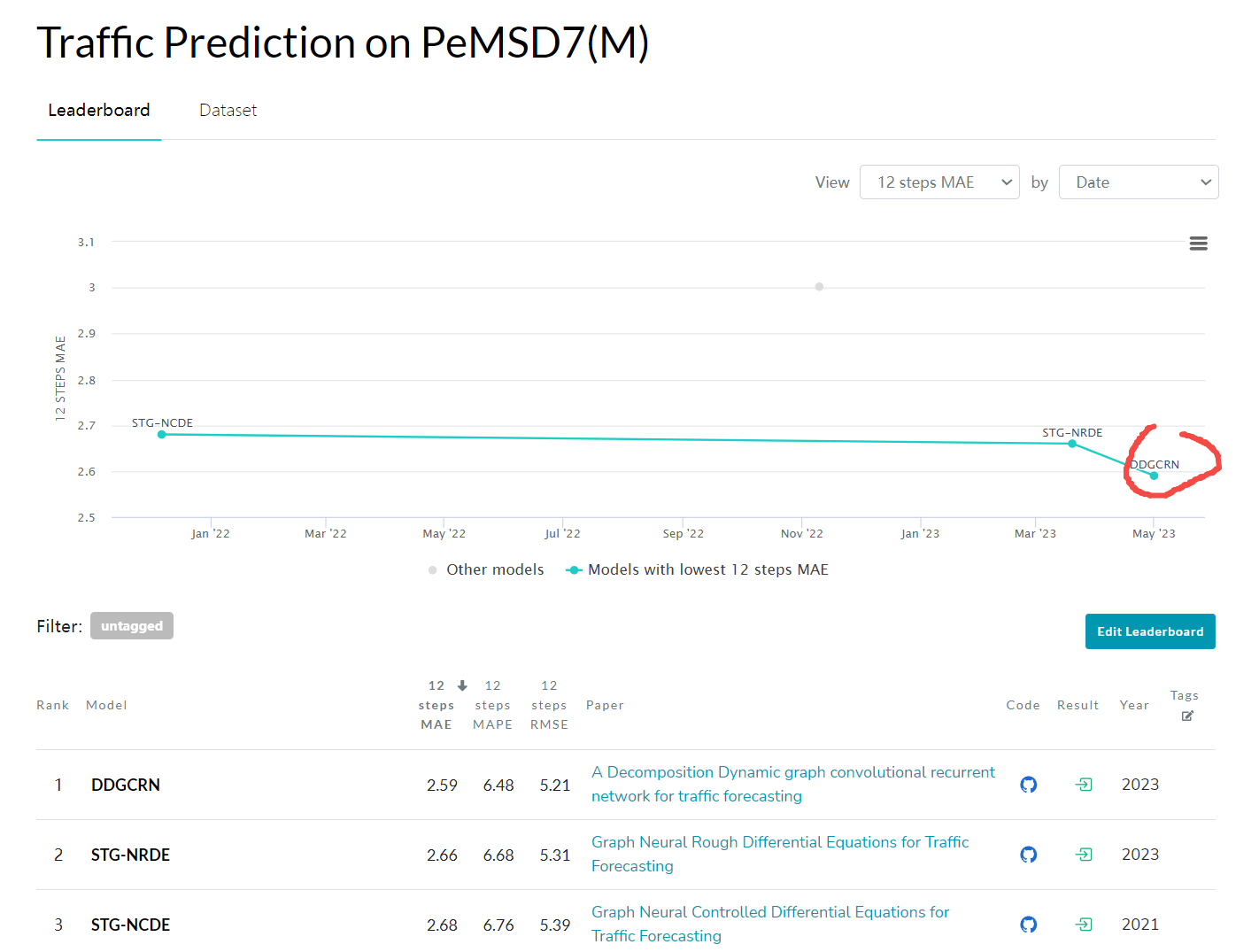
數據集含義

以pems-bay為例，兩個csv文件就是2個矩陣。

vel.csv的形狀是(16384, 325)，代表了16384次觀測數據，每次數據都是325個傳感器的數據（可能是車流量或者車速的一種綜合表達的數據）：

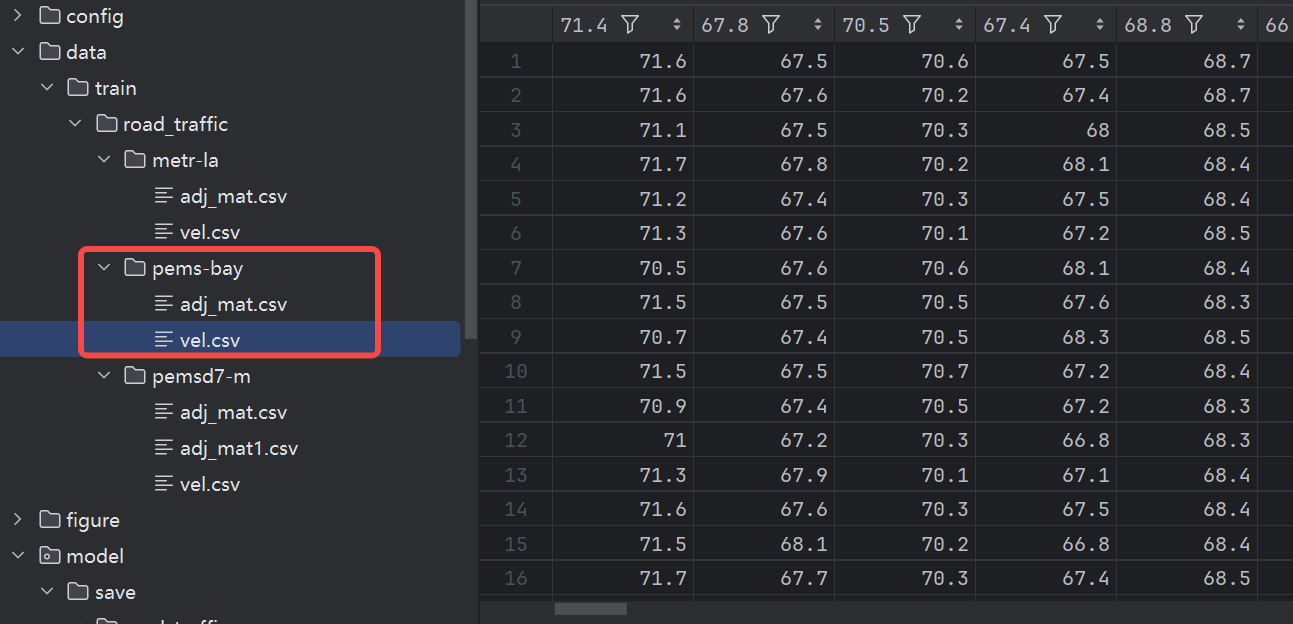
adj.mat.csv的形狀是(325, 325)，表示了傳感器之間的關系，比如距離關系，是鄰接矩陣，鄰接矩陣是對角陣：

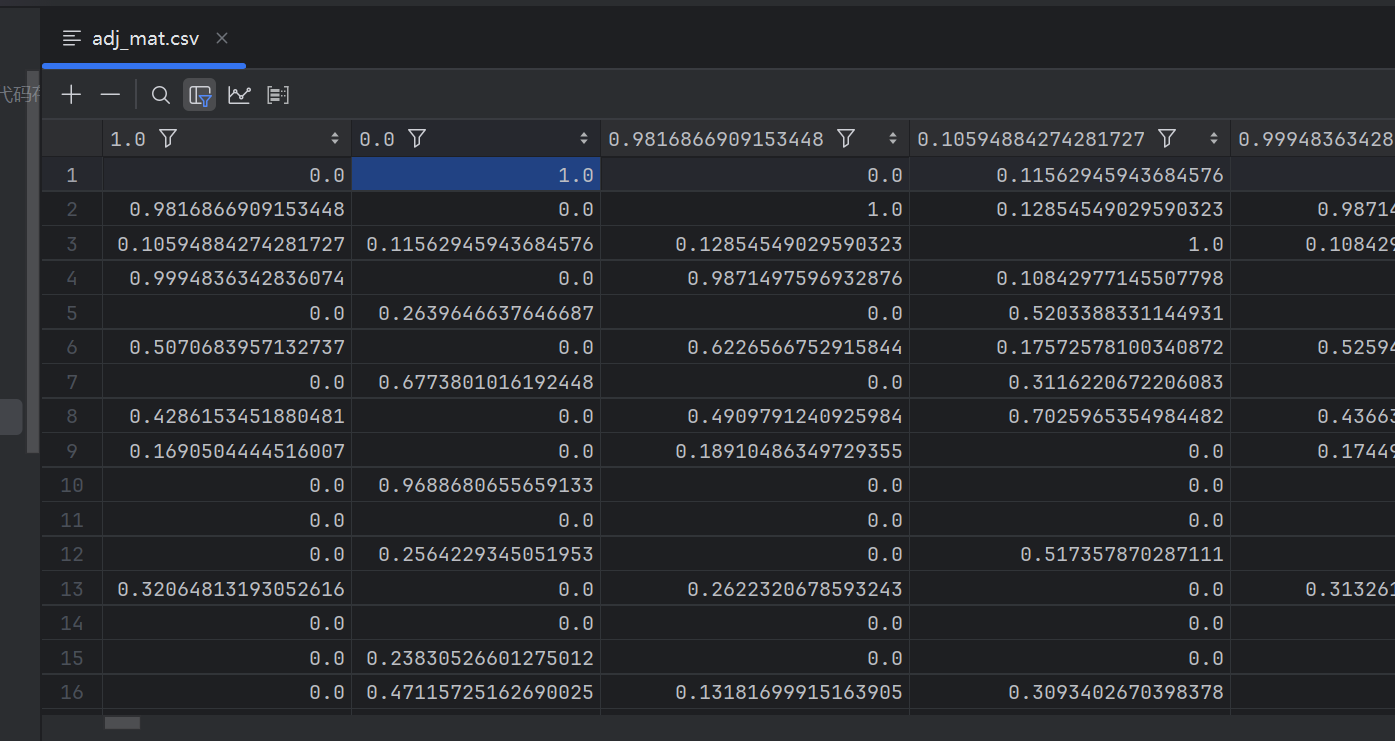
三、任務目標

還是以pems-bay數據集為例子，我們有16384次時序的觀測數據，任務的目標就是預測這325個傳感器的后續數據走向，看看哪個模型預測得準。

交通流量是一個很實際的問題，325個傳感器分布在地區的各個要點中，鄰接矩陣表達了各個傳感器之間的關聯性，而16384次時序觀測數據也表達了傳感器隨時間變化采集到的數據。如果有一個模型可以很好預測傳感器的后續數據，說明模型能很好預測出交通流量走勢，這可以應用到交通疏通中或者預測擁堵的應用里去。

四、訓練過程

基礎推理過程

輸入模型的x大小是，32是batchsize，12是時序步數，325是傳感器維度。

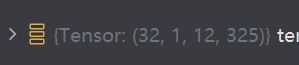
輸出的是下一次時序里的數據：

而訓練數據條數一共有13108條：

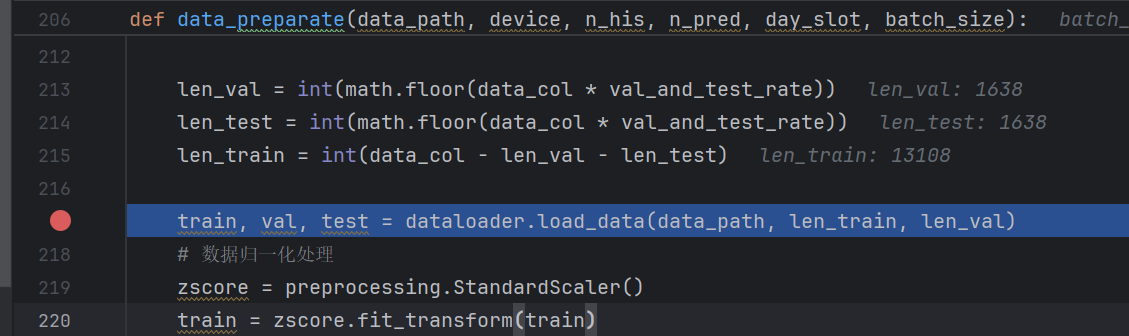
13090/32
409.0625

所以每次訓練是410個iter迭代步數。

x進去后，由self.st_blocks（一系列小波圖運算）運算得到了x_stbs ,

而后 self.output 得到了預測結果。

    def forward(self, x):x_stbs = self.st_blocks(x)# [2, 1, 12, 207]->[2, 64, 4, 207]if self.Ko > 1:x_out = self.output(x_stbs)

鄰接矩陣

在上述推理過程中，在哪里使用到鄰接矩陣了？

在最開始用wavelet_basis來確定了小波基矩陣。

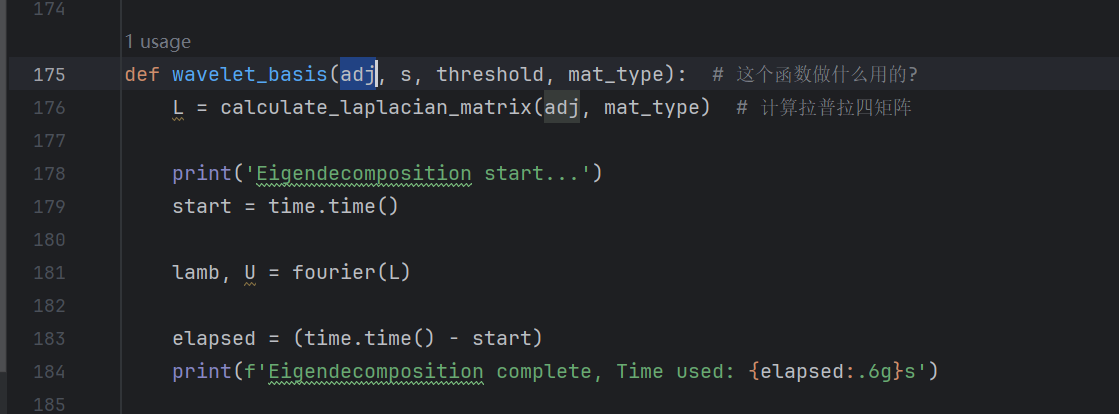
這個函數wavelet_basis的主要作用是根據輸入的交通流量傳感器的鄰接矩陣adj（表示傳感器之間的連接關系），以及參數s（小波尺度參數）和threshold（閾值），來計算并返回一組小波基矩陣，用于后續在圖卷積過程中對信號進行多尺度分析。這個過程涉及圖信號處理的核心步驟，包括拉普拉斯矩陣的計算、特征分解、小波變換的構建、閾值化處理和L1范數歸一化。下面是各部分的詳細解析：

1. 計算拉普拉斯矩陣:

   • 函數首先調用calculate_laplacian_matrix來計算圖的拉普拉斯矩陣L。拉普拉斯矩陣是圖論中的重要概念，廣泛用于圖信號處理和圖的譜分析，能體現圖的拓撲結構。

2. 特征分解:

   • 接著，使用fourier函數對拉普拉斯矩陣L進行特征分解，得到特征值lamb和特征向量矩陣U。這一步是圖傅里葉變換的基礎，用于將信號映射到頻域進行分析。

3. 構建圖小波:

   • 利用weight_wavelet函數基于小波尺度s、特征值lamb和特征向量U計算小波權重矩陣Weight，以及通過weight_wavelet_inverse計算逆小波權重矩陣inverse_Weight。這兩個矩陣是構建小波基的關鍵，用于對信號進行多尺度分解和重構。

4. 閾值化處理:

   • 根據給定的threshold，將Weight和inverse_Weight中小于該閾值的元素設為0，這是一種常見的去噪操作，可以減少噪聲影響，提升模型的穩健性。

5. L1范數歸一化:

   • 對Weight和inverse_Weight進行L1范數歸一化，確保每個行的絕對值之和為1，這有助于保持能量守恒，并使后續的操作（如圖卷積）更加穩定。

6. 轉換格式:

   • 最后，將矩陣轉換為稀疏矩陣格式coo_matrix，以節省存儲空間和加速后續的矩陣運算。

整個函數的輸出t_k = (Weight, inverse_Weight)是一對小波基矩陣，它們在基于小波變換的圖卷積神經網絡（如之前提到的Graph_WaveletsConv）中扮演核心角色，用于捕捉不同尺度的圖信號特征，增強模型對復雜時空數據的理解能力。

注意力機制

小波變換真是復雜的作用機制，大體來說，是將有用信息用小波變換方式給入到了模型前向傳導。

為了引入自注意力機制，就得找一些層引入，小波卷積層是一個不錯的層。

定義一個AttentionModule，它接受節點特征作為輸入，通過兩層全連接層和ReLU激活函數計算每個節點的注意力分數，然后通過softmax函數標準化這些分數，確保所有節點的注意力權重之和為1。在Graph_WaveletsConvWithAttention中，首先使用原有的小波圖卷積操作處理輸入，然后將得到的特征傳遞給注意力模塊，實現特征的自適應加權。

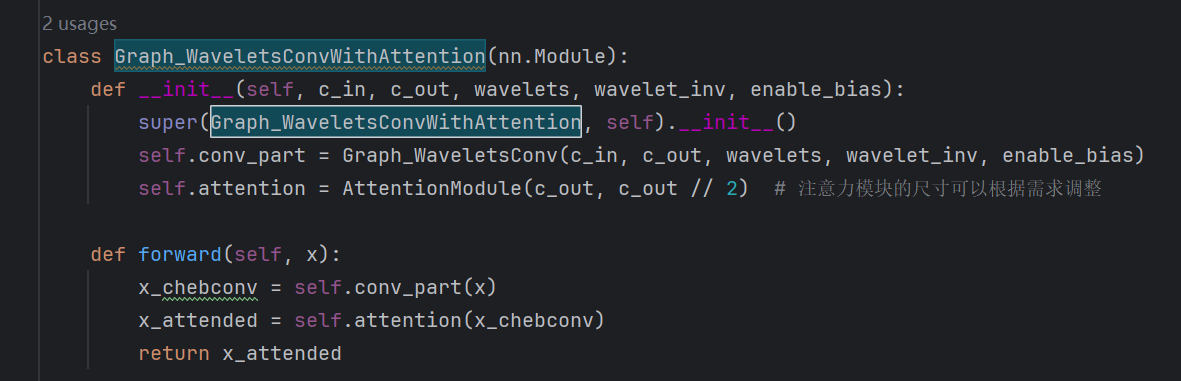
整體結構在多個尺度會調用上注意力塊Graph_WaveletsConvWithAttention：

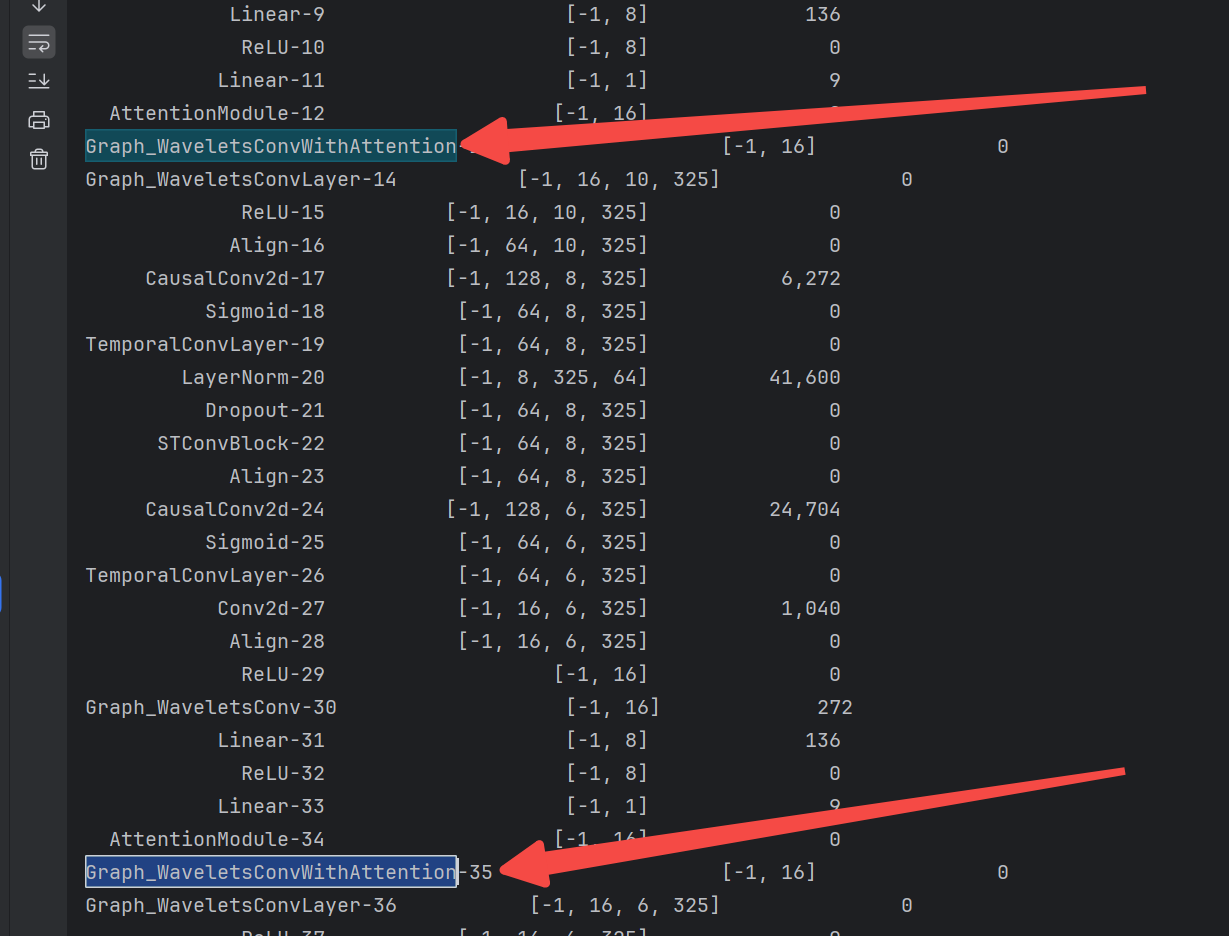
效果是沒有提升，沒提升是正常的，如果一個簡單的改進就能得到提升，那大家都好發論文了：

又試了一下沒加注意力之前的模型，如論文所寫，的確小波加進去，MAE為1.81：

五、 總結

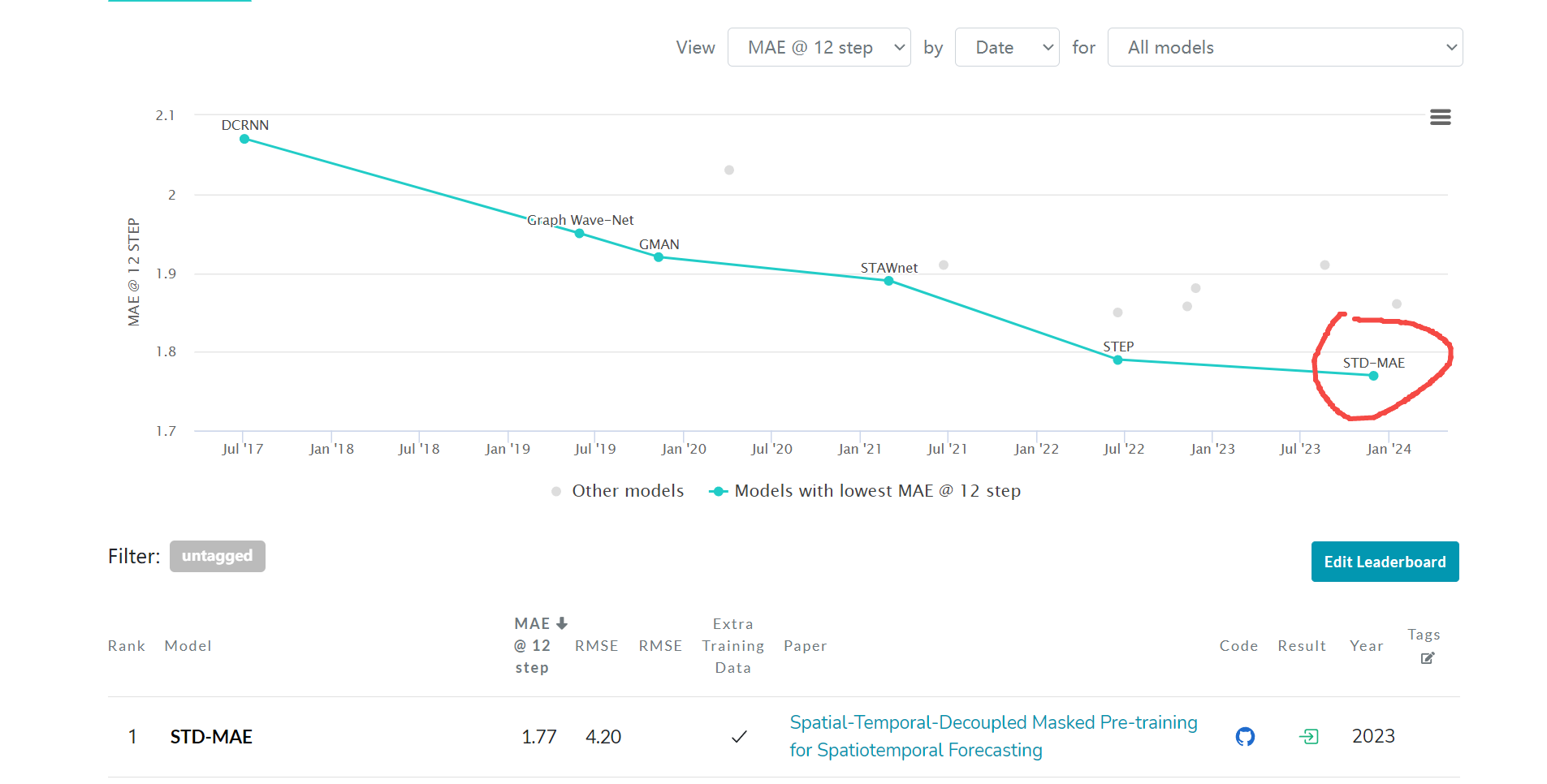
綜合來看，以普通方式改進STGCN是很難有提升的，而目前的SOTA算法非常厲害，比如
STD-MAE算法（Spatial-Temporal-Decoupled Masked Pre-training for Spatiotemporal Forecasting）在PEMS-BAY的指標MAE為 1.77， 或許要嘗試一些別的改進方式才行，我這里就不再進行額外嘗試了。