總結自：【算法設計與分析】期末考試突擊課_嗶哩嗶哩_bilibili

1.遞歸，遞歸方程

1.1遞歸條件:

1.一個問題的解可以分解為幾個子問題的解；

2.這個問題與分解之后的子問題，除了數據規模不同，求解思路完全一樣;

3.存在遞歸終止條件。

1.2遞歸方程的建立，求解

1.2.1建立

當算法包含調用自身的過程時，其運行時間可用遞歸方程描述，

下面是遞歸方程建立的具體過程:假設問題規模為"，T(m)為解決該問題的時間開銷。

1.2.2求解

常用的求解遞歸方程的方法有兩種:替換方法和主定理

1.2.2.1替換方法

用替換方法解某個遞歸方程時，分為兩步。
首先是猜測問題解的某個界限，然后用數學歸納法證明所猜測解的正確性。猜測問題的界限可以根據經驗猜，也可以把遞歸方程逐項展開，再對項進行合并根據合并結果猜測問題的界限。

1.2.2.2主定理（較簡單，套公式即可）

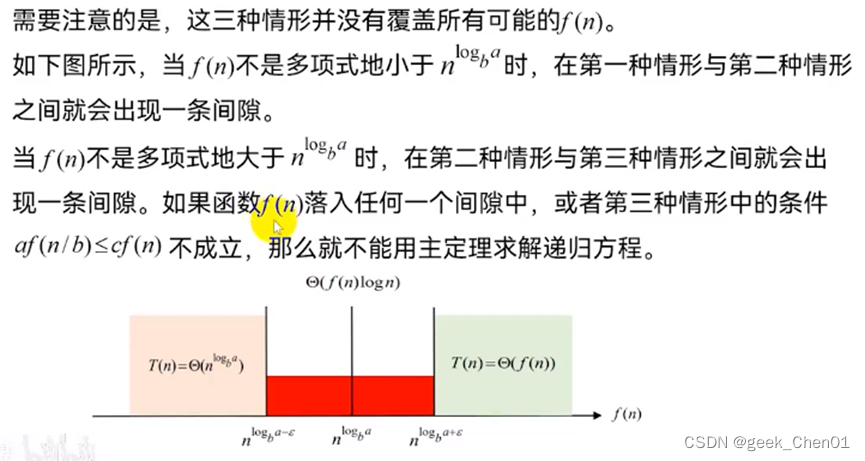
1.2.2.3主定理不能解決的部分：

1.2.3例題

斐波那契序列，歐幾里得算法，漢諾塔，階乘；

1.2.3.1替換方法例題:

1.2.3.2主定理例題:

1.2.3.3 參考答案

T1:

T2:

T3:

T4:

T5:

T6:

T7:

1.3 分治法

分治法的思想：