其它高階數據結構②_圖（概念+存儲+遍歷+最小生成樹）

1. 圖的概念

2. 圖的存儲結構

2.1 鄰接矩陣（后面算法所用）

2.2 鄰接表

3. 圖的遍歷

3.1?BFS廣度優先遍歷

3.2?DFS深度優先遍歷

4.?最小生成樹

4.1 Kruskal算法

4.2 Prim算法

本篇完。

1. 圖的概念

圖是由頂點集合及頂點間的關系組成的一種數據結構：G = (V， E)，其中：

頂點集合V = {x|x屬于某個數據對象集}是有窮非空集合；
E = {(x,y)|x,y屬于V}或者E = {<x, y>|x,y屬于V && Path(x, y)}是頂點間關系的有窮集合，也叫做邊的集合。
(x, y)表示x到y的一條雙向通路，即(x, y)是無方向的；Path(x, y)表示從x到y的一條單向通路，即Path(x, y)是有方向的。
頂點和邊：圖中結點稱為頂點，第i個頂點記作vi。兩個頂點vi和vj相關聯稱作頂點vi和頂點vj之間有一條邊，圖中的第k條邊記作ek，ek = (vi，vj)或<vi，vj>。
有向圖和無向圖：在有向圖中，頂點對<x, y>是有序的，頂點對<x，y>稱為頂點x到頂點y的一條邊(弧)，<x, y>和<y, x>是兩條不同的邊，比如下圖G3和G4為有向圖。在無向圖中，頂點對(x, y)是無序的，頂點對(x,y)稱為頂點x和頂點y相關聯的一條邊，這條邊沒有特定方向，(x, y)和(y，x)是同一條邊，比如下圖G1和G2為無向圖。注意：無向邊(x, y)等于有向邊<x, y>和<y, x>。

完全圖：在有n個頂點的無向圖中，若有n * (n-1)/2條邊，即任意兩個頂點之間有且僅有一條邊，則稱此圖為無向完全圖，比如上圖G1；在n個頂點的有向圖中，若有n * (n-1)條邊，即任意兩個頂點之間有且僅有方向相反的邊，則稱此圖為有向完全圖，比如下圖G4。

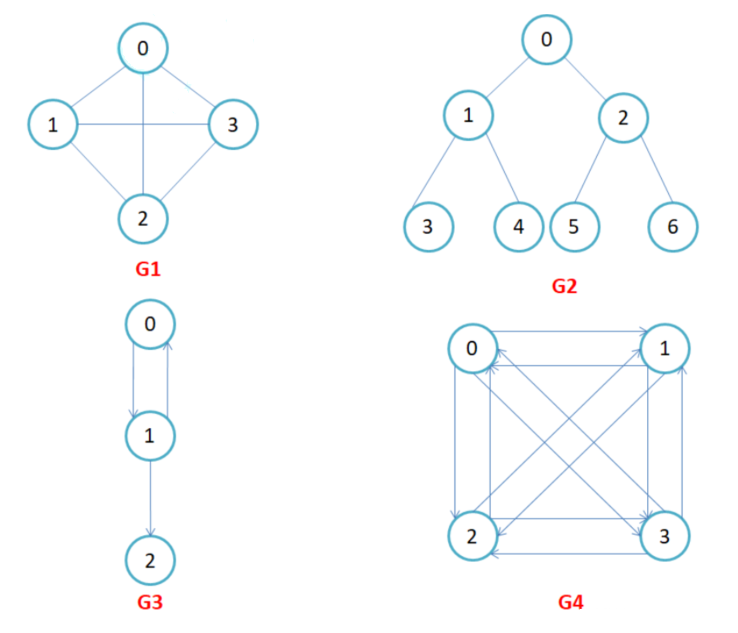
鄰接頂點：在無向圖中G中，若(u, v)是E(G)中的一條邊，則稱u和v互為鄰接頂點，并稱邊(u,v)依附于頂點u和v；在有向圖G中，若<u, v>是E(G)中的一條邊，則稱頂點u鄰接到v，頂點v鄰接自頂點u，并稱邊<u, v>與頂點u和頂點v相關聯。
頂點的度：頂點v的度是指與它相關聯的邊的條數，記作deg(v)。在有向圖中，頂點的度等于該頂點的入度與出度之和，其中頂點v的入度是以v為終點的有向邊的條數，記作indev(v);頂點v的出度是以v為起始點的有向邊的條數，記作outdev(v)。因此：dev(v) = indev(v) + outdev(v)。注意：對于無向圖，頂點的度等于該頂點的入度和出度，即dev(v) = indev(v) = outdev(v)。
路徑：在圖G = (V， E)中，若從頂點vi出發有一組邊使其可到達頂點vj，則稱頂點vi到頂點vj的頂點序列為從頂點vi到頂點vj的路徑。
路徑長度：對于不帶權的圖，一條路徑的路徑長度是指該路徑上的邊的條數；對于帶權的圖，一條路徑的路徑長度是指該路徑上各個邊權值的總和。

帶權圖示例：

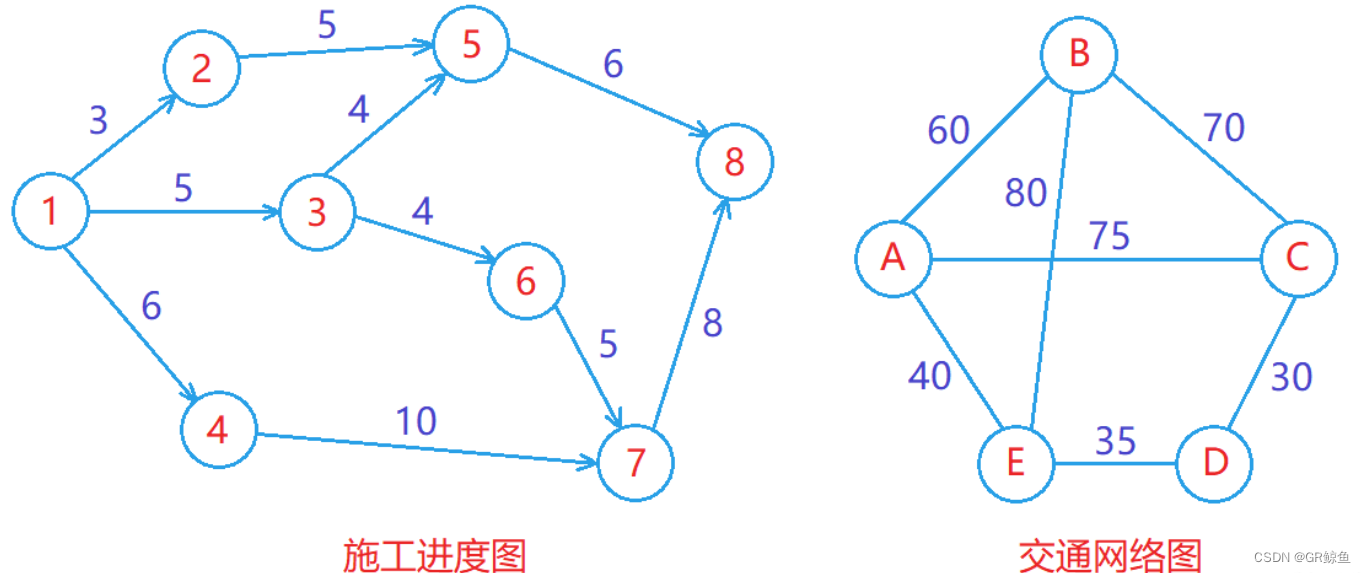
簡單路徑與回路：

若路徑上的各個頂點均不相同，則稱這樣的路徑為簡單路徑。
若路徑上第一個頂點與最后一個頂點相同，則稱這樣的路徑為回路或環。

如下圖：

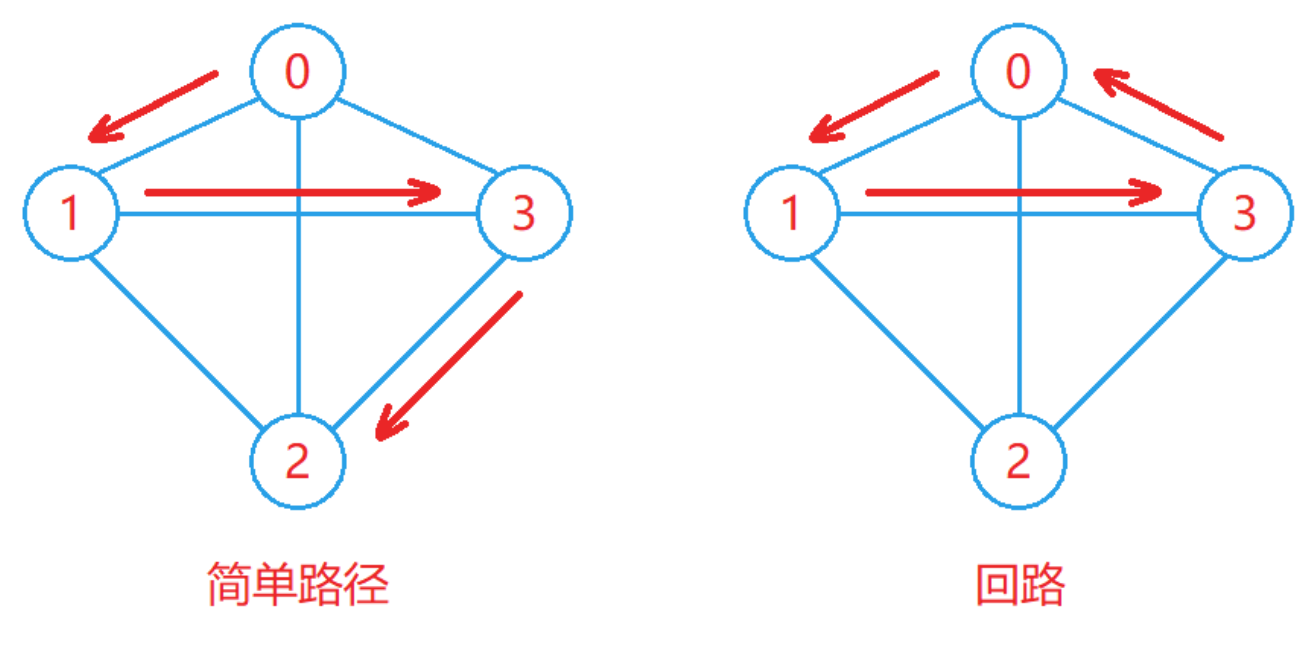
子圖：設圖G = {V, E}和圖G1 = {V1，E1}，若V1屬于V且E1屬于E，則稱G1是G的子圖。

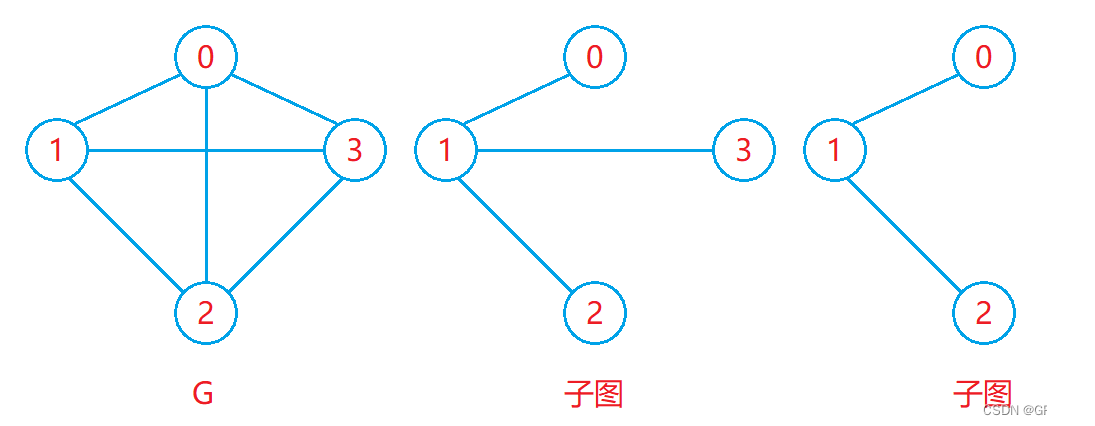
連通圖：在無向圖中，若從頂點v1到頂點v2有路徑，則稱頂點v1與頂點v2是連通的。如果圖中任意一對頂點都是連通的，則稱此圖為連通圖。
強連通圖：在有向圖中，若在每一對頂點vi和vj之間都存在一條從vi到vj的路徑，也存在一條從vj 到 vi的路徑，則稱此圖是強連通圖。
生成樹：一個連通圖的最小連通子圖稱作該圖的生成樹。有n個頂點的連通圖的生成樹有n個頂點和n - 1條邊。
最小生成樹：一個圖的生成樹中，總權值最小的生成樹。

圖常見的表示場景如下：

交通網絡：圖中的每個頂點表示一個地點，圖中的邊表示這兩個地點之間是否有直接相連的公路，邊的權值可以是這兩個地點之間的距離、高鐵時間等。
網絡設備拓撲：圖中的每個頂點表示網絡中的一個設備，圖中的邊表示這兩個設備之間是否可以互傳數據，邊的權值可以是這兩個設備之間傳輸數據所需的時間、丟包的概率等。
社交網絡：圖中的每個頂點表示一個人，圖中的邊表示這兩個人是否互相認識，邊的權值可以是這兩個人之間的親密度、共同好友個數等。

關于有向圖和無向圖：

交通網絡對應的圖可以是有向圖，也可以是無向圖，無向圖對應就是雙向車道，有向圖對應就是單向車道。
網絡設備拓撲對應的圖通常是無向圖，兩個設備之間有邊表示這兩個設備之間可以互相收發數據。
社交網絡對應的圖可以是有向圖，也可以是無向圖，無向圖通常表示一些強社交關系，比如QQ、微信等（一定互為好友），有向圖通常表示一些弱社交關系，比如微博、抖音（不一定互相關注）。

圖的其他相關作用：

在交通網絡中，根據最短路徑算法計算兩個地點之間的最短路徑，根據最小生成樹算法得到將各個地點連通起來所需的最小成本。
在社交網絡中，根據廣度優先搜索得到兩個人之間的共同好友進行好友推薦，根據入邊表和出邊表得知有哪些粉絲以及關注了哪些博主。

圖與樹的聯系與區別：

樹是一種有向無環且連通的圖（空樹除外），但圖并不一定是樹。
有 n 個結點的樹必須有 n ? 1條邊，而圖中邊的數量不取決于頂點的數量。
樹通常用于存儲數據，并快速查找目標數據，而圖通常用于表示某種場景。

2. 圖的存儲結構

圖由頂點和邊組成，存儲圖本質就是將圖中的頂點和邊存儲起來。

本篇博客的各種關于圖的算法都用圖的領接矩陣實現。

2.1 鄰接矩陣（后面算法所用）

鄰接矩陣存儲圖的方式如下：

用一個數組存儲頂點集合，頂點所在位置的下標作為該頂點的編號（所給頂點可能不是整型）。
用一個二維數組 matrix 存儲邊的集合，其中 matrix[i][j]表示編號為 i 和 j?的兩個頂點之間的關系。

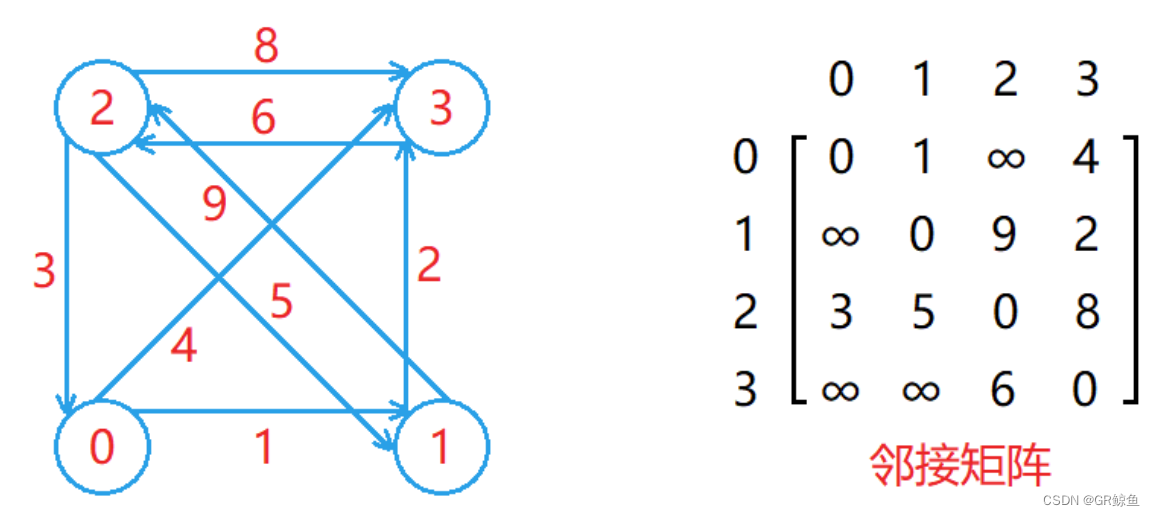
注意事項：

對于不帶權的圖，兩個頂點之間要么相連，要么不相連，可以用0和1表示，matrix [ i ] [ j ]?為1表示編號為 i 和 j 的兩個頂點相連，為0表示不相連。
對于帶權的圖，連接兩個頂點的邊會帶有一個權值，可以用這個權值來設置對應matrix [ i ] [ j ]的值，如果兩個頂點不相連，則使用不會出現的權值進行設置即可（圖中為無窮大）。
對于無向圖來說，頂點 i 和頂點 j 相連，那么頂點 j 就和頂點 i 相連，因此無向圖對應的鄰接矩陣是一個對稱矩陣，即matrix [ i ] [ j ] 的值等于matrix [ i ] [ j ]的值。
在鄰接矩陣中，第 i 行元素中有效權值的個數就是編號為 i 的頂點的出度，第 i 列元素中有效元素的個數就是編號為 i 的頂點的入度。

鄰接矩陣的優點：

鄰接矩陣適合存儲稠密圖，因為存儲稠密圖和稀疏圖時所開辟的二維數組大小是相同的，因此圖中的邊越多，鄰接矩陣的優勢就越明顯。
鄰接矩陣能夠O（1）地判斷兩個頂點是否相連，并獲得相連邊的權值。

鄰接矩陣的缺點：

鄰接矩陣不適合查找一個頂點連接出去的所有邊，需要遍歷矩陣中對應的一行，該過程的時間復雜度是O ( N )? ，其中 N?表示的是頂點的個數。

鄰接矩陣的實現：

#pragma once#include <vector>
#include <iostream>
#include <string>
#include <queue>
#include <map>
#include <set>
#include <functional>
using namespace std;namespace Matrix // 臨接矩陣
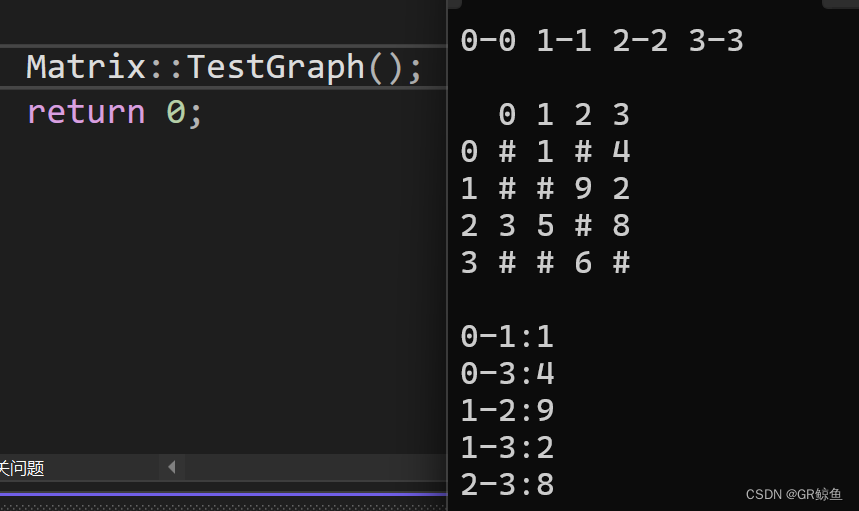
{template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>class Graph //Vertex頂點，Weight權值，MAX_W不存在邊的標識值 ，Direction有向無向{private:vector<V> _vertexs; // 頂點集合map<V, size_t> _vIndexMap; // 頂點映射下標vector<vector<W>> _matrix; // 存儲邊集合的矩陣（領接矩陣）public:struct Edge{V _srci;V _dsti;W _w;Edge(const V& srci, const V& dsti, const W& w):_srci(srci), _dsti(dsti), _w(w){}bool operator<(const Edge& eg) const{return _w < eg._w;}bool operator>(const Edge& eg) const{return _w > eg._w;}};typedef Graph<V, W, MAX_W, Direction> Self;Graph() = default;Graph(const V* vertexs, int n): _vertexs(vertexs, vertexs + n) // 設置頂點集合, _matrix(n, vector<int>(n, MAX_W)) // 開辟二維數組空間，MAX_W作為不存在邊的標識值{for (int i = 0; i < n; i++) // 建立頂點與下標的映射關系{_vIndexMap[vertexs[i]] = i;}}size_t GetVertexIndex(const V& v) // 獲取頂點對應的下標{auto ret = _vIndexMap.find(v);if (ret != _vIndexMap.end()) // 頂點存在{return ret->second;}else{throw invalid_argument("不存在的頂點");return -1;}}void _AddEdge(int srci, int dsti, const W& weight){_matrix[srci][dsti] = weight; // 設置鄰接矩陣中對應的值if (Direction == false) // 無向圖{_matrix[dsti][srci] = weight; // 添加從目標頂點到源頂點的邊}}void AddEdge(const V& src, const V& dst, const W& w) // 添加邊{size_t srci = GetVertexIndex(src); // 獲取源頂點和目標頂點的下標size_t dsti = GetVertexIndex(dst);_AddEdge(srci, dsti, w);}void Print(){for (size_t i = 0; i < _vertexs.size(); ++i) // 打印頂點和下標映射關系{cout << _vertexs[i] << "-" << i << " ";}cout << endl << endl;cout << "  ";for (size_t i = 0; i < _vertexs.size(); ++i){cout << i << " ";}cout << endl;for (size_t i = 0; i < _matrix.size(); ++i) // 打印矩陣{cout << i << " ";for (size_t j = 0; j < _matrix[i].size(); ++j){if (_matrix[i][j] != MAX_W)cout << _matrix[i][j] << " ";elsecout << "#" << " ";}cout << endl;}cout << endl;for (size_t i = 0; i < _matrix.size(); ++i) // 打印所有的邊{for (size_t j = 0; j < _matrix[i].size(); ++j){if (i < j && _matrix[i][j] != MAX_W){cout << _vertexs[i] << "-" << _vertexs[j] << ":" << _matrix[i][j] << endl;}}}}};void TestGraph(){Graph<char, int, INT_MAX, true> g("0123", 4);g.AddEdge('0', '1', 1);g.AddEdge('0', '3', 4);g.AddEdge('1', '3', 2);g.AddEdge('1', '2', 9);g.AddEdge('2', '3', 8);g.AddEdge('2', '1', 5);g.AddEdge('2', '0', 3);g.AddEdge('3', '2', 6);g.Print();}
}

2.2 鄰接表

鄰接表（類似哈希桶）：使用數組存儲頂點的集合，使用鏈表存儲頂點的關系（邊）。

鄰接表存儲圖的方式如下：

用一個數組存儲頂點集合，頂點所在的位置的下標作為該頂點的編號（所給頂點可能不是整型）。
用一個出邊表存儲從各個頂點連接出去的邊，出邊表中下標為 i 的位置存儲的是從編號為 i 的頂點連接出去的邊。
用一個入邊表存儲連接到各個頂點的邊，入邊表中下標為 i 的位置存儲的是連接到編號為 i?的頂點的邊。

如下圖：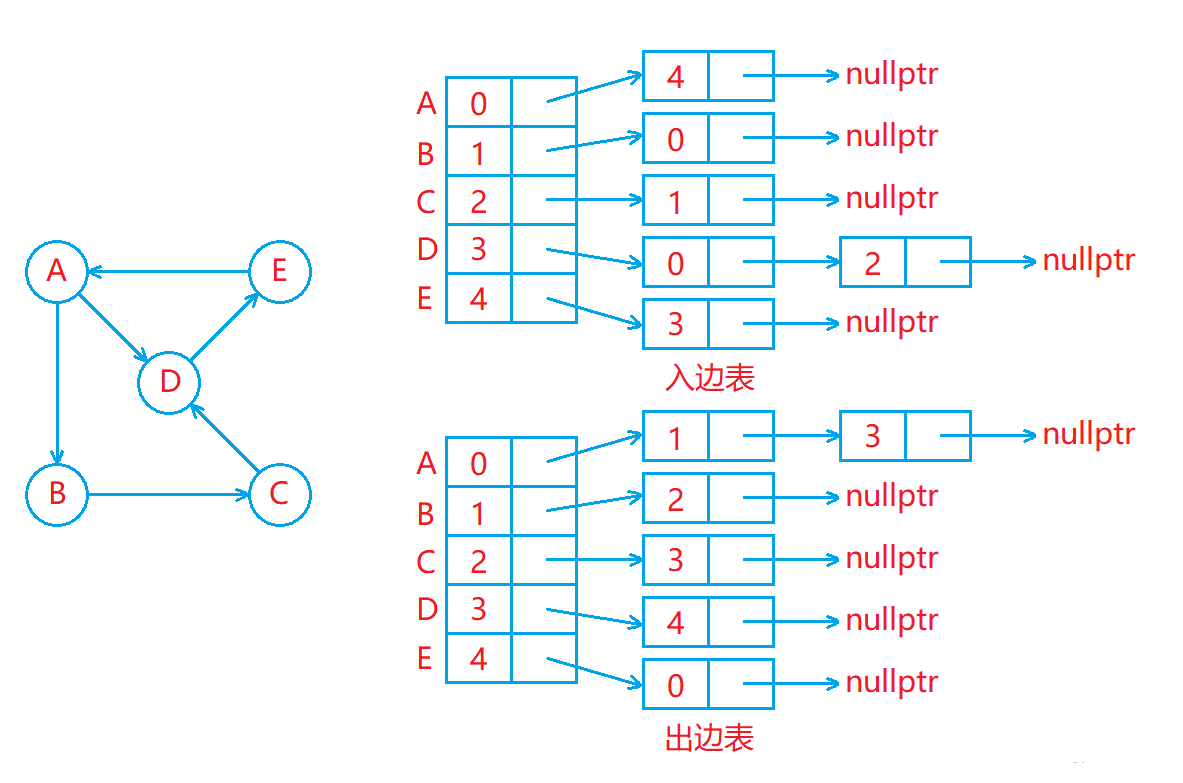

出邊表和入邊表類似于哈希桶，其中每個位置存儲的都是一個鏈表，出邊表中下標為 i 的位置的鏈表中存儲的都是從編號為 i 的頂點連接出去的邊，入邊表中下標為 i 的位置的鏈表中存儲的都是連接到編號為 i 的頂點的邊。
在鄰接表中，出邊表中下標為 i 的位置的鏈表中元素的個數就是編號為 i 的頂點的出度，入邊表中下標為 i 的的位置的鏈表中元素的個數就是編號為 i 的頂點的入度。
在實現鄰接表時，一般只需要用一個出邊表來存儲從各個頂點連接出去的邊即可，因為大多數情況下都是需要從一個頂點出發找與其相連的其他頂點，所以一般不需要存儲入邊表。

鄰接表的優點：

鄰接表適合存儲稀疏圖，因為鄰接表存儲圖時開辟的空間大小取決于邊的數量，圖中邊的數量越少，鄰接表存儲邊時所需的內存空間就越少。
鄰接表適合查找一個頂點連接出去的所有邊，出邊表中下標為 i 的位置的鏈表中存儲的就是從頂點 i 連接出去的所有邊。

鄰接表的缺點：

鄰接表不適合確定兩個頂點是否相連，需要遍歷出邊表中源頂點對應位置的鏈表，該過程的時間復雜度是O（E），其中 E 表示從源頂點連接出去的邊的數量。

鄰接表的實現：

#pragma once#include <vector>
#include <iostream>
#include <string>
#include <queue>
#include <map>
#include <set>
#include <functional>
using namespace std;namespace LinkTable // 臨接表
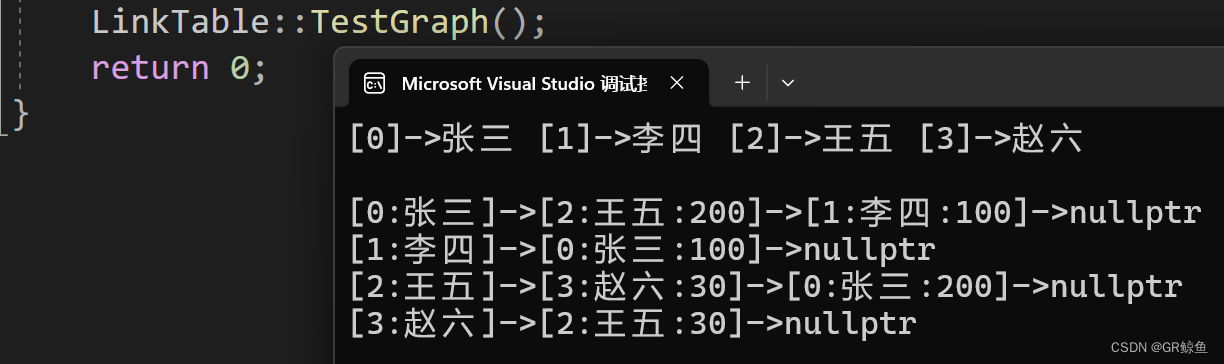
{template<class W>struct LinkEdge{int _srcIndex;int _dstIndex;W _w;LinkEdge<W>* _next;LinkEdge(const W& w): _srcIndex(-1), _dstIndex(-1), _w(w), _next(nullptr){}};template<class V, class W, bool Direction = false>class Graph // 構造函數{typedef LinkEdge<W> Edge;private:map<string, int> _vIndexMap;vector<V> _vertexs;			 // 頂點集合vector<Edge*> _linkTable;    // 邊的集合的臨接表public:Graph(const V* vertexs, size_t n) // 構造函數{_vertexs.reserve(n); // 設置頂點集合for (size_t i = 0; i < n; ++i){_vertexs.push_back(vertexs[i]);_vIndexMap[vertexs[i]] = i; // 建立頂點與下標的映射關系}_linkTable.resize(n, nullptr); // 開辟鄰接表的空間}size_t GetVertexIndex(const V& v) // 獲取頂點對應的下標{auto ret = _vIndexMap.find(v);if (ret != _vIndexMap.end()) // 頂點存在{return ret->second;}else{throw invalid_argument("不存在的頂點");return -1;}}void AddEdge(const V& src, const V& dst, const W& w) // 添加邊{size_t srcindex = GetVertexIndex(src);size_t dstindex = GetVertexIndex(dst);Edge* sd_edge = new Edge(w); // 添加從源頂點到目標頂點的邊sd_edge->_srcIndex = srcindex;sd_edge->_dstIndex = dstindex;sd_edge->_next = _linkTable[srcindex];_linkTable[srcindex] = sd_edge;if (Direction == false) // 1 0 無向圖{Edge* ds_edge = new Edge(w); // 添加從目標頂點到源頂點的邊ds_edge->_srcIndex = dstindex;ds_edge->_dstIndex = srcindex;ds_edge->_next = _linkTable[dstindex];_linkTable[dstindex] = ds_edge;}}void print() // 打印頂點集合和鄰接表{int n = _vertexs.size();for (int i = 0; i < n; i++) // 打印頂點集合{cout << "[" << i << "]->" << _vertexs[i] << " ";}cout << endl << endl;for (int i = 0; i < n; i++) // 打印鄰接表{Edge* cur = _linkTable[i];cout << "[" << i << ":" << _vertexs[i] << "]->";while (cur){cout << "[" << cur->_dstIndex << ":" << _vertexs[cur->_dstIndex] << ":" << cur->_w << "]->";cur = cur->_next;}cout << "nullptr" << endl;}}};void TestGraph(){string a[] = { "張三", "李四", "王五", "趙六" };Graph<string, int> g1(a, 4);g1.AddEdge("張三", "李四", 100);g1.AddEdge("張三", "王五", 200);g1.AddEdge("王五", "趙六", 30);g1.print();}
}

3. 圖的遍歷

圖的遍歷指的是遍歷圖中的頂點，主要有BFS廣度優先遍歷和DFS深度優先遍歷兩種方式。

3.1?BFS廣度優先遍歷

????????廣度優先遍歷又稱BFS，其遍歷過程類似于二叉樹的層序遍歷，從起始頂點開始一層一層向外進行遍歷。

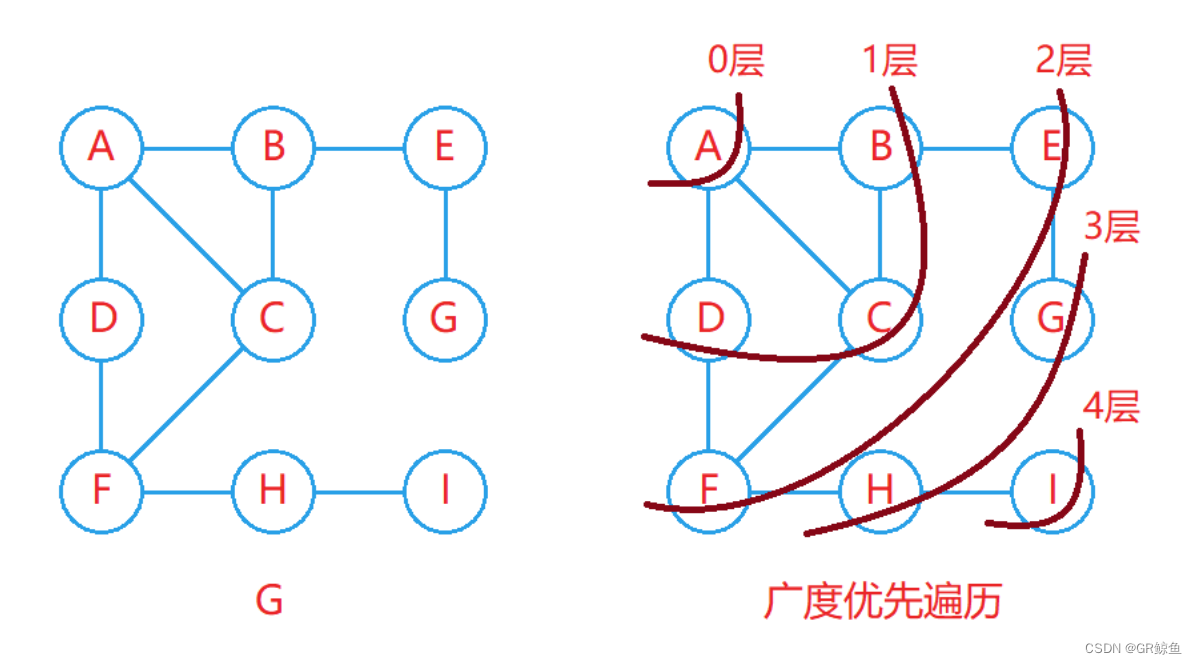
廣度優先遍歷的實現：

廣度優先遍歷需要借助一個隊列和一個標記數組，利用隊列先進先出的特點實現一層一層向外遍歷，利用標記數組來記錄各個頂點是否被訪問過。
剛開始時將起始頂點入隊列，并將起始頂點標記為訪問過，然后不斷從隊列中取出頂點進行訪問，并判斷該頂點是否有鄰接頂點，如果有鄰接頂點并且該鄰接頂點沒有被訪問過，則將該鄰接頂點入隊列，并在入隊列后立即將該鄰接頂點標記為訪問過。

代碼如下：

namespace Matrix // 臨接矩陣
{template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>class Graph //Vertex頂點，Weight權值，MAX_W不存在邊的標識值 ，Direction有向無向{private:vector<V> _vertexs; // 頂點集合map<V, size_t> _vIndexMap; // 頂點映射下標vector<vector<W>> _matrix; // 存儲邊集合的矩陣（領接矩陣）public:void BFS(const V& src){size_t srci = GetVertexIndex(src);queue<int> q; // 隊列和標記數組vector<bool> visited(_vertexs.size(), false);q.push(srci);visited[srci] = true;int levelSize = 1;size_t n = _vertexs.size();while (!q.empty()){for (int i = 0; i < levelSize; ++i) // 一層一層出{int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << " ";for (size_t i = 0; i < n; ++i) // 把front頂點的鄰接頂點入隊列{if (_matrix[front][i] != MAX_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}cout << endl;levelSize = q.size();}cout << endl;}}void TestGraphBFS(){string a[] = { "張三", "李四", "王五", "趙六", "周七" };Graph<string, int> g1(a, sizeof(a) / sizeof(string));g1.AddEdge("張三", "李四", 100);g1.AddEdge("張三", "王五", 200);g1.AddEdge("王五", "趙六", 30);g1.AddEdge("王五", "周七", 30);g1.BFS("張三");}
}

為了防止頂點被重復加入隊列導致死循環，因此需要一個標記數組，當一個頂點被訪問過后就不應該再將其加入隊列了。
如果當一個頂點從隊列中取出訪問時才再將其標記為訪問過，也可能會存在頂點被重復加入隊列的情況，比如當圖中的頂點B出隊列時，頂點C作為頂點B的鄰接頂點并且還沒有被訪問過（頂點C還在隊列中），此時頂點C就會再次被加入隊列，因此最好在一個頂點被入隊列時就將其標記為訪問過。
如果所給圖不是一個連通圖，那么從一個頂點開始進行廣度優先遍歷，無法遍歷完圖中的所有頂點，這時可以遍歷標記數組，查看哪些頂點還沒有被訪問過，對于沒有被訪問過的頂點，則從該頂點處繼續進行廣度優先遍歷，直到圖中所有的頂點都被訪問過。

3.2?DFS深度優先遍歷

???????深度優先遍歷又稱DFS，其遍歷過程類似于二叉樹的先序遍歷，從起始頂點開始不斷對頂點進行深入遍歷。?????

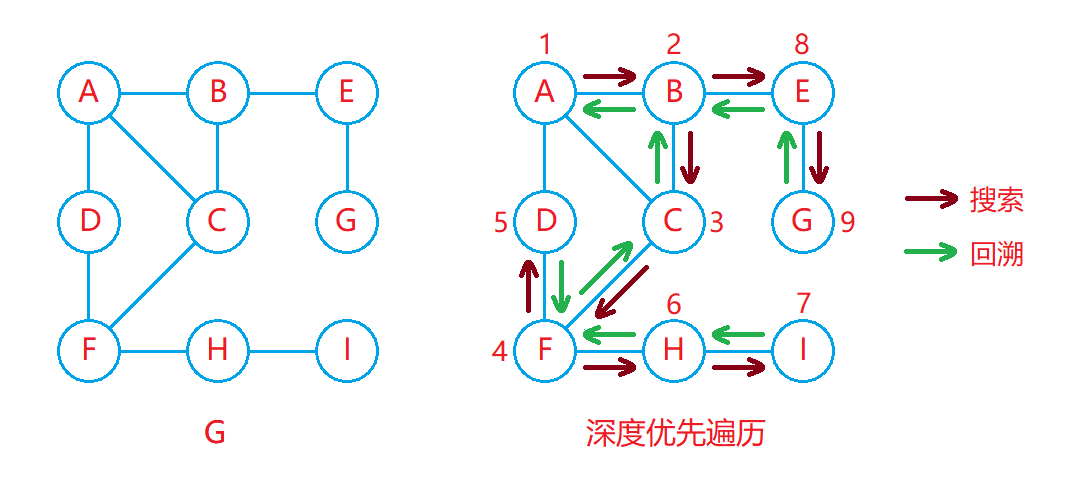
深度優先遍歷的實現：

深度優先遍歷可以通過遞歸實現，同時也需要借助一個標記數組來記錄各個頂點是否被訪問過。
從起始頂點處開始進行遞歸遍歷，在遍歷過程中先對當前頂點進行訪問，并將其標記為訪問過，然后判斷該頂點是否有鄰接頂點，如果有鄰接頂點并且該鄰接頂點沒有被訪問過，則遞歸遍歷該鄰接頂點。

代碼如下：

namespace Matrix // 臨接矩陣
{template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>class Graph //Vertex頂點，Weight權值，MAX_W不存在邊的標識值 ，Direction有向無向{private:vector<V> _vertexs; // 頂點集合map<V, size_t> _vIndexMap; // 頂點映射下標vector<vector<W>> _matrix; // 存儲邊集合的矩陣（領接矩陣）public:void _DFS(size_t srci, vector<bool>& visited){cout << srci << ":" << _vertexs[srci] << endl;  // 訪問visited[srci] = true; for (size_t i = 0; i < _vertexs.size(); ++i) // 找一個srci相鄰的沒有訪問過的點，深度遍歷{if (_matrix[srci][i] != MAX_W && visited[i] == false) // 鄰接頂點，且沒有被訪問過{_DFS(i, visited);}}}void DFS(const V& src){size_t srci = GetVertexIndex(src); // 起始頂點的下標vector<bool> visited(_vertexs.size(), false);_DFS(srci, visited);}}void TestGraphDFS(){string a[] = { "張三", "李四", "王五", "趙六", "周七" };Graph<string, int> g1(a, sizeof(a) / sizeof(string));g1.AddEdge("張三", "李四", 100);g1.AddEdge("張三", "王五", 200);g1.AddEdge("王五", "趙六", 30);g1.AddEdge("王五", "周七", 30);g1.DFS("張三");}
}

如果所給圖不是一個連通圖，那么從一個頂點開始進行深度優先遍歷，無法遍歷完圖中的所有頂點，這時可以遍歷標記數組，查看哪些頂點還沒有被訪問過，對于沒有被訪問過的頂點，則從該頂點處繼續進行深度優先遍歷，直到圖中所有的頂點都被訪問過。

4.?最小生成樹

最小生成樹的概念：

一個連通圖的最小連通子圖稱為該圖的生成樹，若連通圖由 n 個頂點組成，則其生成樹必含 n 個頂點和 n ? 1 條邊，最小生成樹指的是一個圖的生成樹中，總權值最小的生成樹。
連通圖中的每一棵生成樹都是原圖的一個極大無環子圖，從其中刪去任何一條邊，生成樹就不再連通，在其中引入任何一條新邊，都會形成一條回路。

注意事項：

對于各個頂點來說，除了第一個頂點之外，其他每個頂點想要連接到圖中，至少需要一條邊使其連接進來，所以由 n 個頂點的連通圖的生成樹有 n 個頂點和 n ? 1 條邊。
對于生成樹來說，圖中的每個頂點已經連通了，如果再引入一條新邊，那么必然會使得被新邊相連的兩個頂點之間存在一條直接路徑和一條間接路徑，即形成回路。
最小生成樹是圖的生成樹中總權值最小的生成樹，生成樹是圖的最小連通子圖，而連通圖是無向圖的概念，有向圖對應的是強連通圖，所以最小生成樹算法的處理對象都是無向圖。

構成最小生成樹的準則：

只能使用圖中的邊來構造最小生成樹。
只能使用恰好 n ? 1 條邊來連接圖中的 n 個頂點。
選用的 n ? 1 條邊不能構成回路。

構造最小生成樹的算法有Kruskal算法和Prim算法，這兩個算法都采用了逐步求解的貪心策略。

Kruskal算法是全局最優的策略，而Prim算法是局部最優的策略。

4.1 Kruskal算法

Kruskal算法（克魯斯卡爾算法）的基本思想如下：

構造一個含 n 個頂點、不含任何邊的圖作為最小生成樹，對原圖中的各個邊按權值進行排序。
每次從原圖中選出一條最小權值的邊，將其加入到最小生成樹中，如果加入這條邊會使得最小生成樹中構成回路，則重新選擇一條邊。
按照上述規則不斷選邊，當選出 n ? 1 條合法的邊時，則說明最小生成樹構造完畢，如果無法選出 n ? 1 條合法的邊，則說明原圖不存在最小生成樹。

動圖演示：（注意到選7，不選6，就是不能構成環）

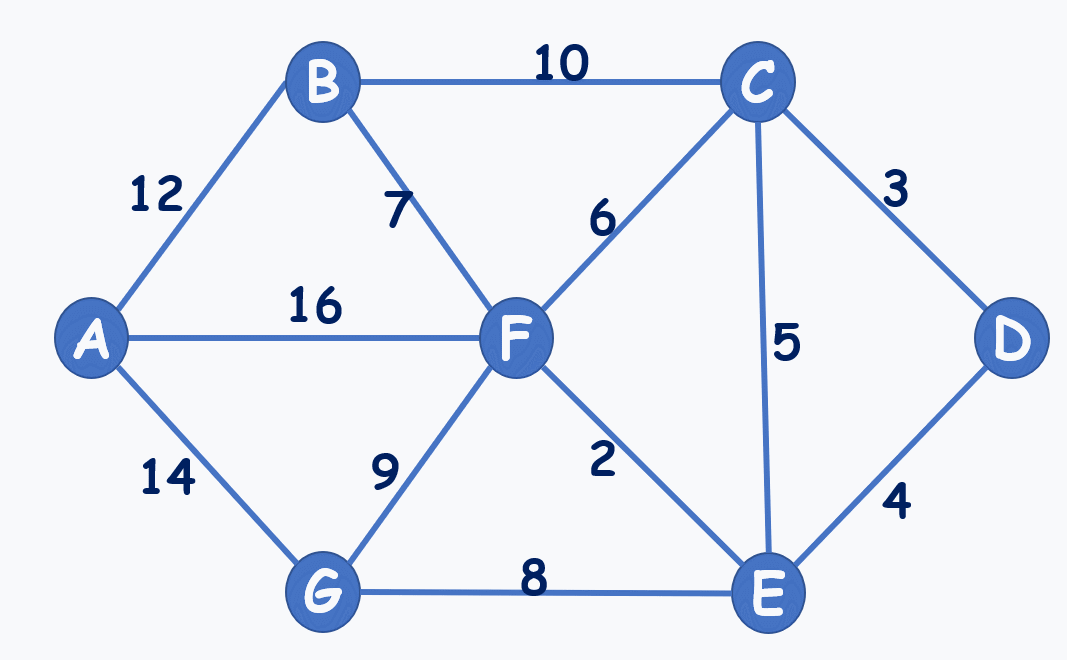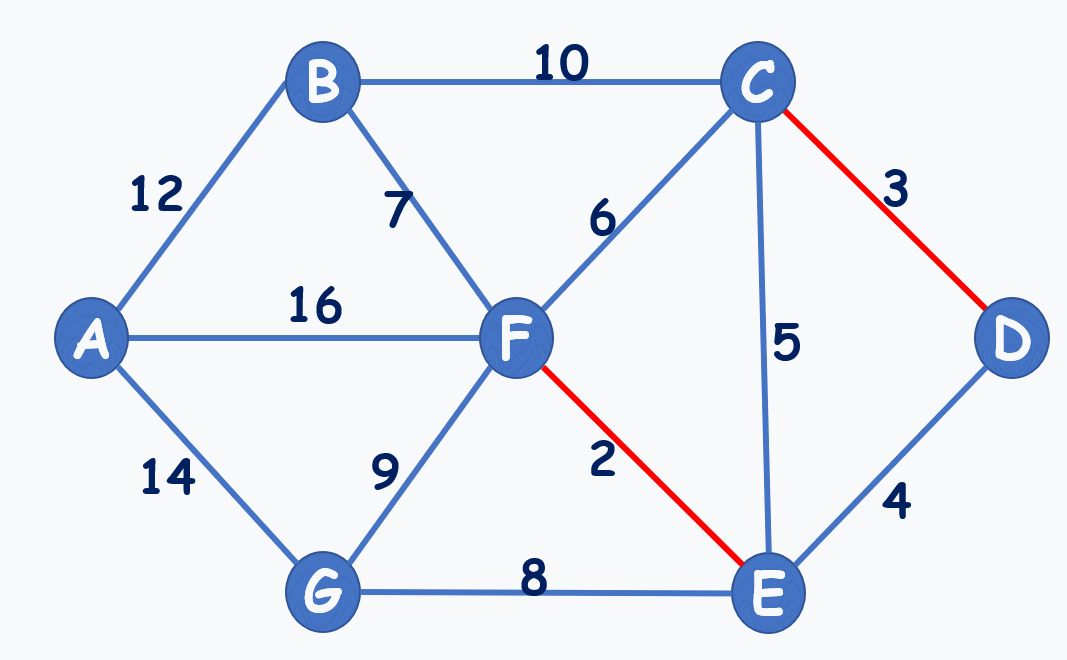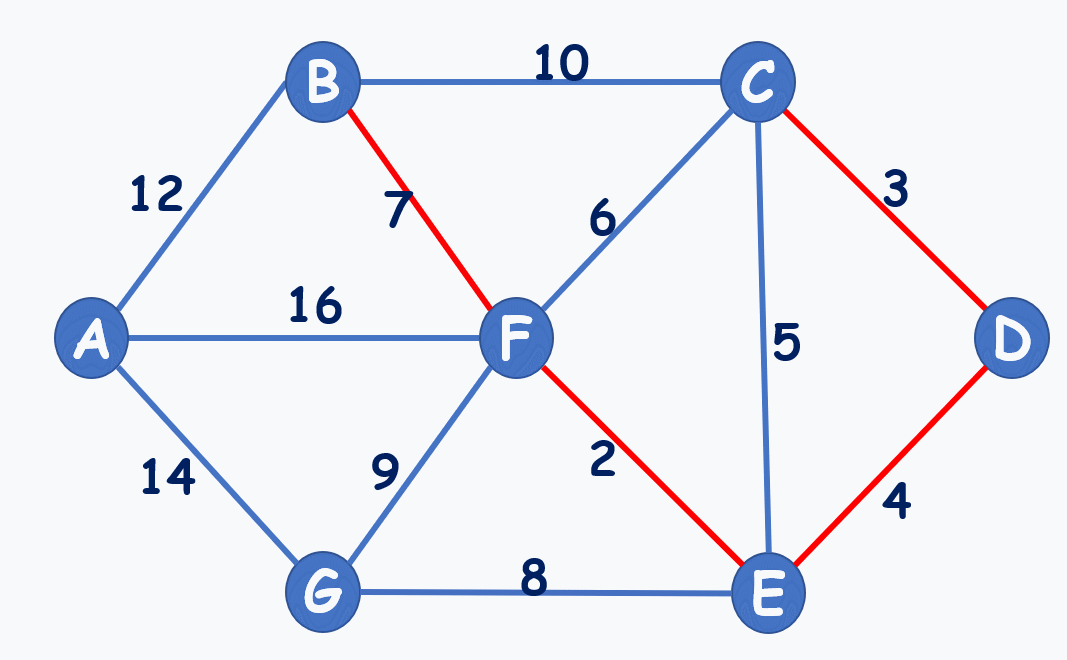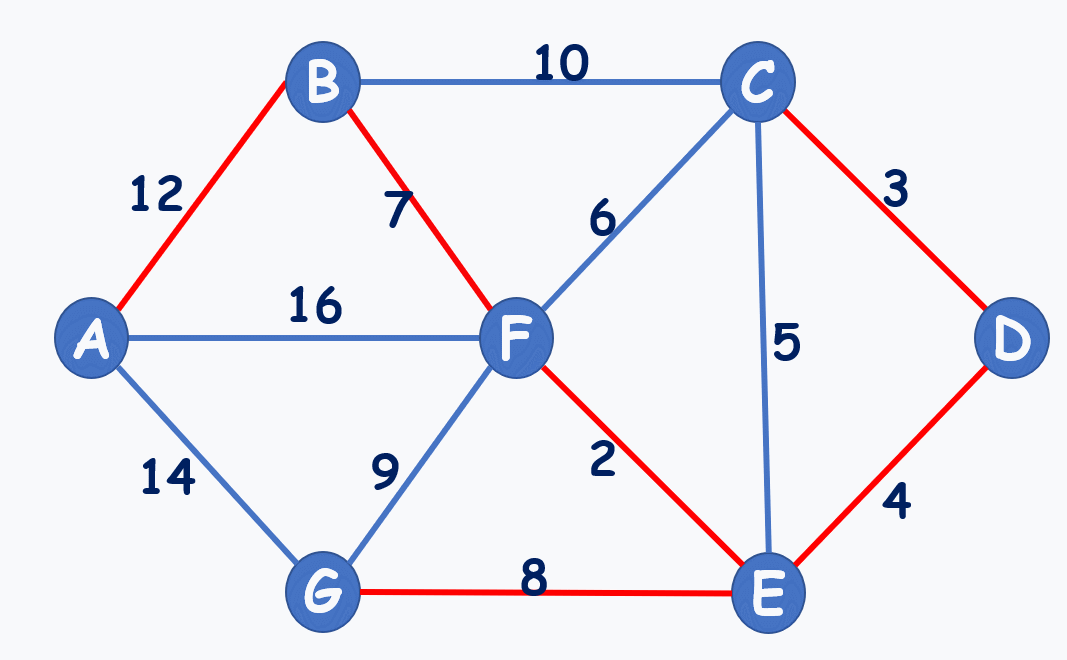
再貼個動圖：

以下是《算法導論》里對Kruskal算法的步驟圖解：

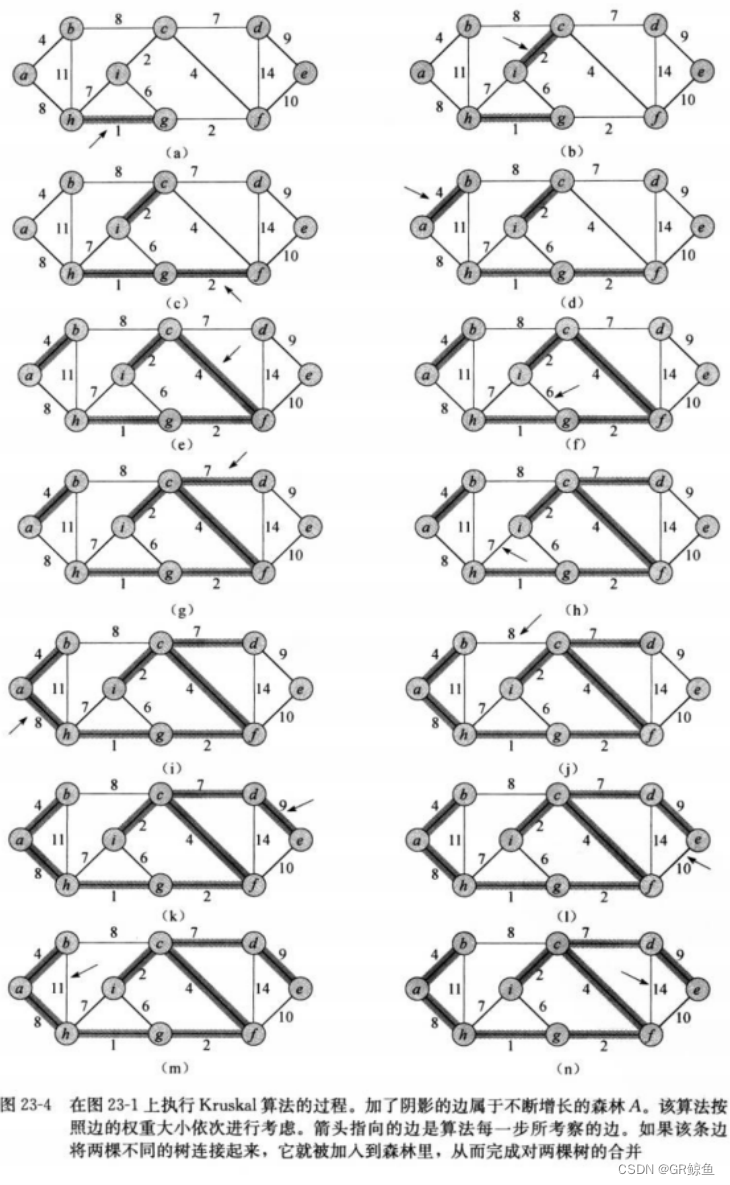
代碼實現：

namespace Matrix // 臨接矩陣
{template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>class Graph //Vertex頂點，Weight權值，MAX_W不存在邊的標識值 ，Direction有向無向{private:vector<V> _vertexs; // 頂點集合，頂點所在位置的下標作為該頂點的編號map<V, size_t> _vIndexMap; // 頂點映射下標vector<vector<W>> _matrix; // 存儲邊集合的矩陣，_matrix[i][j]表示編號為i和j的兩個頂點之間的關系public:struct Edge{V _srci;V _dsti;W _w;Edge(const V& srci, const V& dsti, const W& w):_srci(srci), _dsti(dsti), _w(w){}bool operator<(const Edge& eg) const{return _w < eg._w;}bool operator>(const Edge& eg) const{return _w > eg._w;}};void _AddEdge(int srci, int dsti, const W& weight){_matrix[srci][dsti] = weight; // 設置鄰接矩陣中對應的值if (Direction == false) // 無向圖{_matrix[dsti][srci] = weight; // 添加從目標頂點到源頂點的邊}}void AddEdge(const V& src, const V& dst, const W& w) // 添加邊{size_t srci = GetVertexIndex(src); // 獲取源頂點和目標頂點的下標size_t dsti = GetVertexIndex(dst);_AddEdge(srci, dsti, weight);}typedef Graph<V, W, MAX_W, Direction> Self;W Kruskal(Self& minTree) // 克魯斯卡爾算法{int n = _vertexs.size(); // 二維數組空間minTree._vertexs = _vertexs; // 設置最小生成樹的頂點集合minTree._vIndexMap = _vIndexMap; // 設置最小生成樹頂點與下標的映射minTree._matrix.resize(n, vector<W>(n, MAX_W)); // 開辟最小生成樹的二維數組空間priority_queue<Edge, vector<Edge>, greater<Edge>> pq; // 優先級隊列（小堆）for (size_t i = 0; i < n; ++i) // 將所有邊添加到優先級隊列{								// 最小生成樹算法的處理對象都是無向圖for (size_t j = 0; j < i; ++j) // 只遍歷矩陣的一半，避免重復添加相同的邊{if (_matrix[i][j] != MAX_W){pq.push(Edge(i, j, _matrix[i][j]));}}}UnionFindSet ufs(n); // n個頂點的并查集size_t i = 1; // 已選邊的數量，貪心策略，從最小的邊開始選W total = W(); // 總權值while (!pq.empty() && i < n){Edge min = pq.top(); // 從優先級隊列中獲取一個權值最小的邊pq.pop();// 邊不在一個集合，說明不會構成環，則添加到最小生成樹if (ufs.InSet(min._srci, min._dsti)){// cout << _vertexs[min._srci] << "-" << _vertexs[min._dsti] << ":"// << _matrix[min._srci][min._dsti] << endl;minTree._AddEdge(min._srci, min._dsti, min._w); // 在最小生成樹中添加邊total += min._w;ufs.Union(min._srci, min._dsti);++i;cout << "選邊: " << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;}else // 邊的源頂點和目標頂點在同一個集合，加入這條邊會構成環{cout << "成環: " << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;}}if (i == n){cout << "構建最小生成樹成功" << endl;return total;}else{cout << "無法構成最小生成樹" << endl;return W();}}}
}

在獲取圖的最小生成樹時，會以無參的方式定義一個最小生成樹對象，然后用原圖對象調用上述Kruskal函數，通過輸出型參數的方式獲取原圖的最小生成樹，由于我們定義了一個帶參的構造函數，使得編譯器不再生成默認構造函數，因此需要通過default關鍵字強制生成Graph類的默認構造函數。
一條邊包含兩個頂點和邊的權值，可以定義一個Edge結構體來描述一條邊，結構體內包含邊的源頂點和目標頂點的下標以及邊的權值，在使用優先級隊列構造小堆結構時，需要存儲的對象之間能夠支持 > 運算符操作，因此需要對Edge結構體的 > 運算符進行重載，將其重載為邊的權值的比較。
當選出的邊不會構成回路時，需要將這條邊插入到最小生成樹對應的圖中，此時已經知道了這條邊的源頂點和目標頂點對應的下標，可以在Graph類中新增一個_AddEdge子函數，該函數支持通過源頂點和目標頂點的下標向圖中插入邊，而Graph類中原有的AddEdge函數可以復用這個_AddEdge子函數。
最小生成樹不一定是唯一的，特別是當原圖中存在很多權值相等的邊的時候，比如對于動圖中的圖來說，將最小生成樹中的 b c 邊換成 a h 邊也是一棵最小生成樹。
上述代碼中通過優先級隊列構造小堆來依次獲取權值最小的邊，也可以通過其他排序算法按權值對邊進行排序，然后按權值從小到大依次遍歷各個邊進行選邊操作。
上述代碼中使用的并查集UnionFindSet類，在本專欄上一篇博客中已經講解過了。

4.2 Prim算法

????????Prim算法是一種解決連通圖最小生成樹問題的貪心算法。最小生成樹是原圖的一個子圖，包含了圖中所有的頂點，并且是一棵樹，使得所有邊的權重之和最小。Prim算法通過逐步選擇頂點來構建最小生成樹。

????????Prim算法的核心思想是從一個初始頂點開始，每次選擇一個與當前最小生成樹相鄰的頂點，將權重最小的邊加入最小生成樹，直到所有頂點都被包含在最小生成樹中。在整個過程中，保持當前最小生成樹的所有頂點都是連通的。Prim算法的每一步都選擇當前最小生成樹與其余頂點之間的最小權重邊，逐步構建最小生成樹。這個過程保證了每一步都是局部最優的，最終得到的最小生成樹是全局最優的。

Prim算法動圖：

Prim算法中的邊選擇：

在Prim算法的執行過程中，每一步都是從已經選擇的頂點集合到未選擇的頂點中選擇一條最小權重的邊。這條邊將一個未選擇的頂點連接到已經選擇的頂點集合中。
由于每一步都是通過選擇連接已有樹和未選擇頂點的最小權重邊，新加入的邊不會形成環。這是因為Prim算法每次都是選擇最小權重的邊，而非隨機選擇。

?無需專門考慮成環問題：

由于Prim算法每一步的選擇都確保了不會形成環，所以無需在算法實現中專門考慮成環問題。
成環問題通常涉及到判斷當前考慮的邊是否會形成環，需要使用一些額外的數據結構（例如并查集）來判斷。Kruskal算法就需要在每一步中判斷加入的邊是否形成環，因此需要處理成環問題。

簡化實現：

由于Prim算法在每一步的選擇中已經考慮了不形成環這一點，實現上更加簡單。Prim算法通常可以通過優先隊列（最小堆）等數據結構來高效地選擇最小權重的邊。
相對而言，Kruskal算法需要額外的成環判斷，通常涉及更復雜的數據結構和算法。

以下是《算法導論》里對Prim算法的介紹：

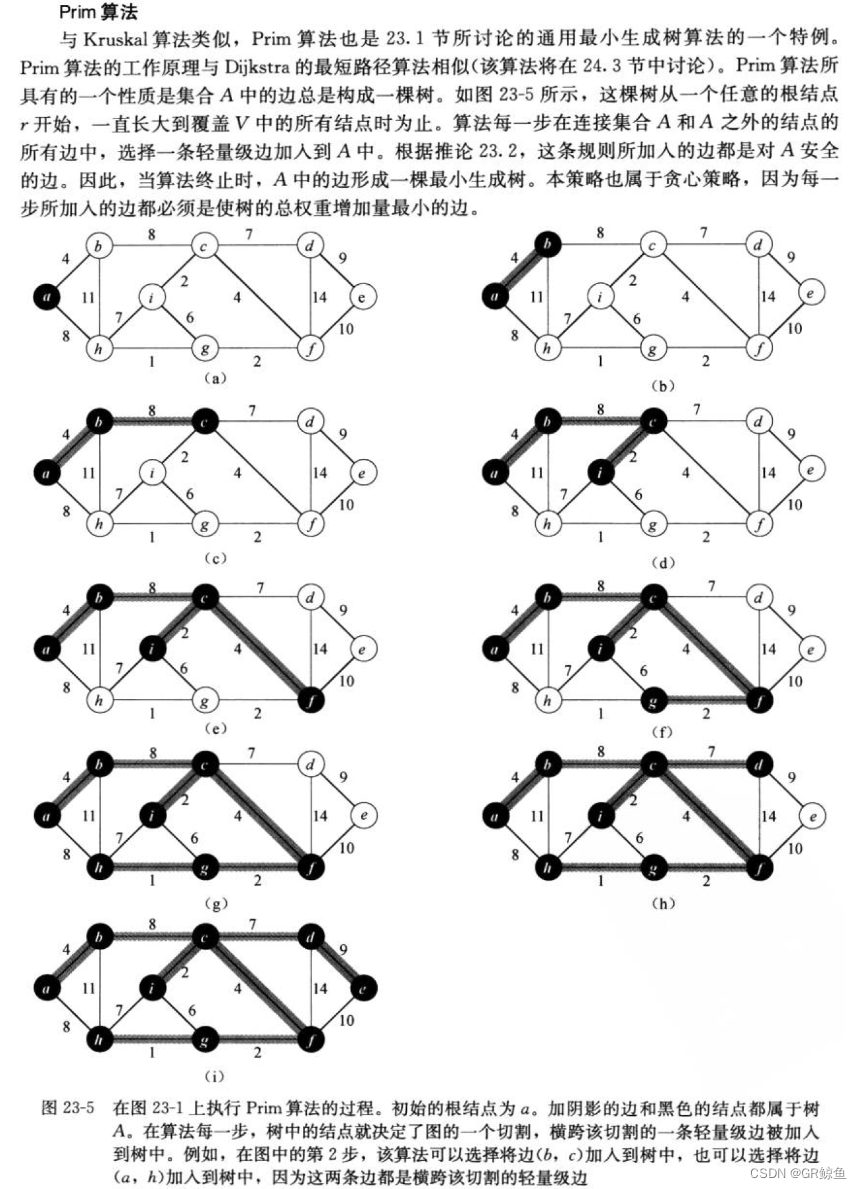
代碼：

namespace Matrix // 臨接矩陣
{template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>class Graph //Vertex頂點，Weight權值，MAX_W不存在邊的標識值 ，Direction有向無向{private:vector<V> _vertexs; // 頂點集合，頂點所在位置的下標作為該頂點的編號map<V, size_t> _vIndexMap; // 頂點映射下標vector<vector<W>> _matrix; // 存儲邊集合的矩陣，_matrix[i][j]表示編號為i和j的兩個頂點之間的關系public:struct Edge{V _srci;V _dsti;W _w;Edge(const V& srci, const V& dsti, const W& w):_srci(srci), _dsti(dsti), _w(w){}bool operator<(const Edge& eg) const{return _w < eg._w;}bool operator>(const Edge& eg) const{return _w > eg._w;}};void _AddEdge(int srci, int dsti, const W& weight){_matrix[srci][dsti] = weight; // 設置鄰接矩陣中對應的值if (Direction == false) // 無向圖{_matrix[dsti][srci] = weight; // 添加從目標頂點到源頂點的邊}}void AddEdge(const V& src, const V& dst, const W& w) // 添加邊{size_t srci = GetVertexIndex(src); // 獲取源頂點和目標頂點的下標size_t dsti = GetVertexIndex(dst);_AddEdge(srci, dsti, weight);}typedef Graph<V, W, MAX_W, Direction> Self;W Prim(Self& minTree, const W& src) // 普里姆算法{size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();minTree._vertexs = _vertexs; // 設置最小生成樹的頂點集合minTree._vIndexMap = _vIndexMap; // 設置最小生成樹頂點與下標的映射minTree._matrix.resize(n, vector<W>(n, MAX_W)); // 開辟最小生成樹的二維數組空間vector<bool> X(n, false); // 已選邊vector<bool> Y(n, true); // 未選邊X[srci] = true;Y[srci] = false;// 從X->Y集合中連接的邊里面選出最小的邊priority_queue<Edge, vector<Edge>, greater<Edge>> minq;for (size_t i = 0; i < n; ++i) // 先把srci連接的邊添加到隊列中{if (_matrix[srci][i] != MAX_W){minq.push(Edge(srci, i, _matrix[srci][i]));}}cout << "Prim開始選邊" << endl;size_t size = 0; // 已選邊數量W totalW = W(); // 最小生成樹的總權值while (!minq.empty()){Edge min = minq.top();minq.pop();if (X[min._dsti]) // 最小邊的目標點也在X集合，則構成環{//cout << "構成環:";//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;}else{minTree._AddEdge(min._srci, min._dsti, min._w);//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;X[min._dsti] = true;Y[min._dsti] = false;++size;totalW += min._w;if (size == n - 1)break;for (size_t i = 0; i < n; ++i){if (_matrix[min._dsti][i] != MAX_W && Y[i]){minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));}}}}if (size == n - 1){cout << "構建最小生成樹成功" << endl;return totalW;}else{cout << "無法構成最小生成樹" << endl;return W();}}}void TestGraphMinTree(){const char str[] = "abcdefghi";Graph<char, int> g(str, strlen(str));g.AddEdge('a', 'b', 4);g.AddEdge('a', 'h', 8);//g.AddEdge('a', 'h', 9);g.AddEdge('b', 'c', 8);g.AddEdge('b', 'h', 11);g.AddEdge('c', 'i', 2);g.AddEdge('c', 'f', 4);g.AddEdge('c', 'd', 7);g.AddEdge('d', 'f', 14);g.AddEdge('d', 'e', 9);g.AddEdge('e', 'f', 10);g.AddEdge('f', 'g', 2);g.AddEdge('g', 'h', 1);g.AddEdge('g', 'i', 6);g.AddEdge('h', 'i', 7);Graph<char, int> kminTree;cout << "Kruskal:" << g.Kruskal(kminTree) << endl;kminTree.Print();cout << endl << endl;Graph<char, int> pminTree;cout << "Prim:" << g.Prim(pminTree, 'a') << endl;pminTree.Print();cout << endl;for (size_t i = 0; i < strlen(str); ++i){cout << "Prim:" << g.Prim(pminTree, str[i]) << endl;}}
}