前言

??1. 添加逗號
??2. 跳臺階
??3. 撲克牌順子

1. 添加逗號

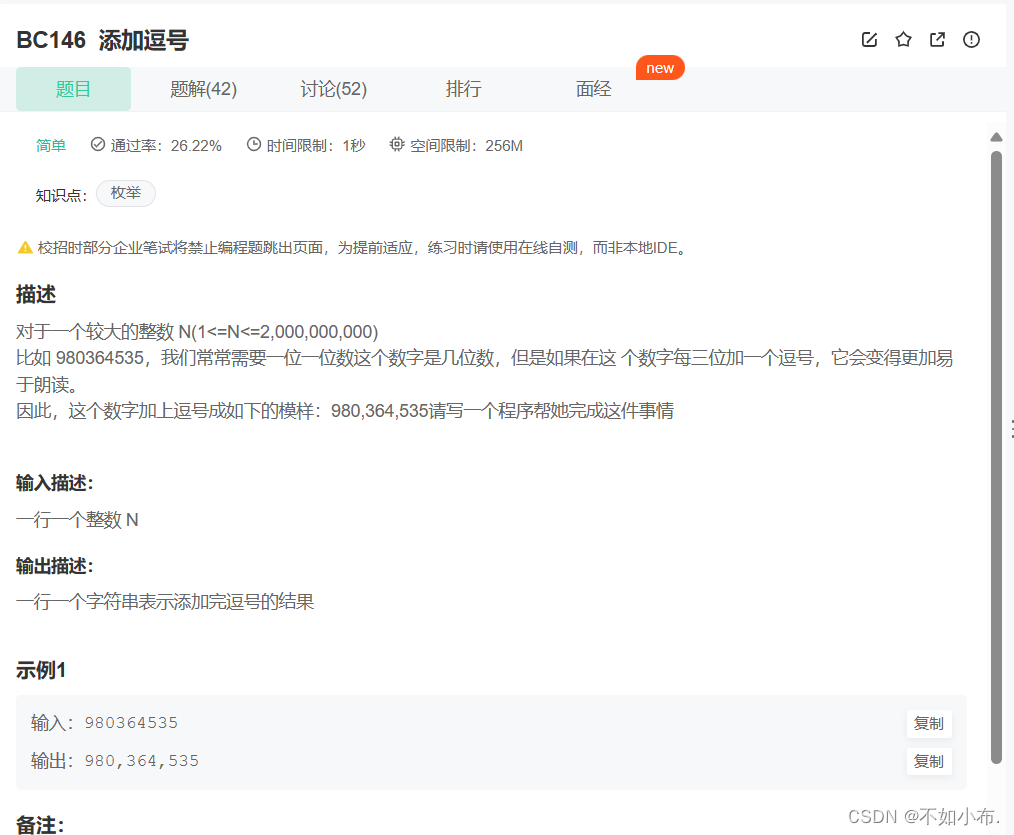
1.1 題目描述

2.2 解題思路

??我的寫法是先進行逆置，然后再創建一個字符串，然后一個一個添加上去，每添加三個字符，就加上一個逗號，結束之后再進行逆置就可以了。（當然也可以直接逆序遍歷，這樣就不需要逆置了）

2.3 代碼實現

#include <iostream>
using namespace std;
#include <string>
#include <algorithm>
int main() 
{string ret, num;cin >> num;reverse(num.begin(), num.end());int n = num.size();int k = 0;while (k < n) {if (k != 0 && k % 3 == 0)ret += ",";ret += num[k++];}reverse(ret.begin(), ret.end());cout << ret;return 0;
}

2. 跳臺階

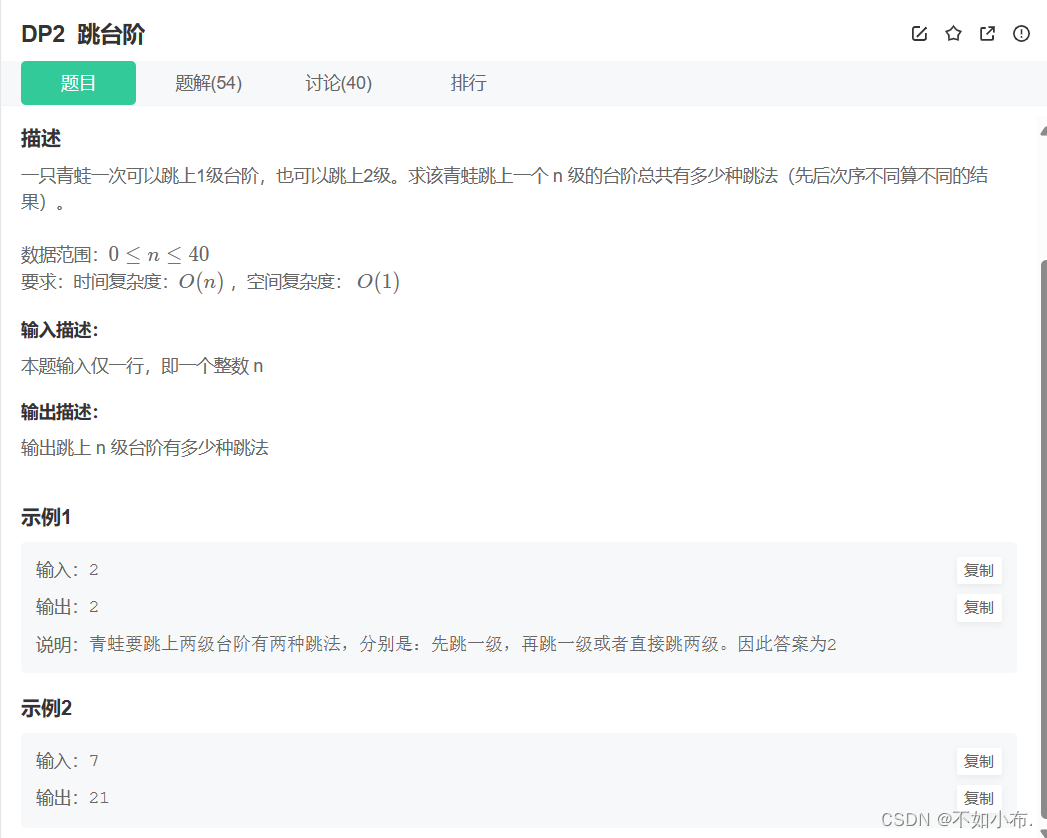
2.1 題目描述

2.2 解題思路

??還是一道簡單的dp問題，大概思路與之前寫的最小花費爬樓梯相差無幾。
??狀態表示：dp[i] -> 到達 i 位置一共有多少跳法。每一個位置的跳法都來源于它前兩個臺階，所以狀態轉移方程就是：dp[i] = dp[i-1] + dp[i-2]。
??還可以進行優化，那就是只用兩個變量來保存一個臺階前兩個臺階的各自的跳法，就像滾動數組一樣，不斷向前就可以了。如果不理解就寫成上面的狀態轉移方程就行了。

2.3 代碼實現

#include <iostream>
using namespace std;
int main() {int n = 0;cin >> n;int dp1 = 1, dp2 = 2;int ret = 0;if (n == 1) ret = 1;else if (n == 2) ret = 2;else {for (int i = 3; i <= n; i++) {ret = dp1 + dp2;dp1 = dp2;dp2 = ret;}}cout << ret;return 0;
}

3. 撲克牌順子

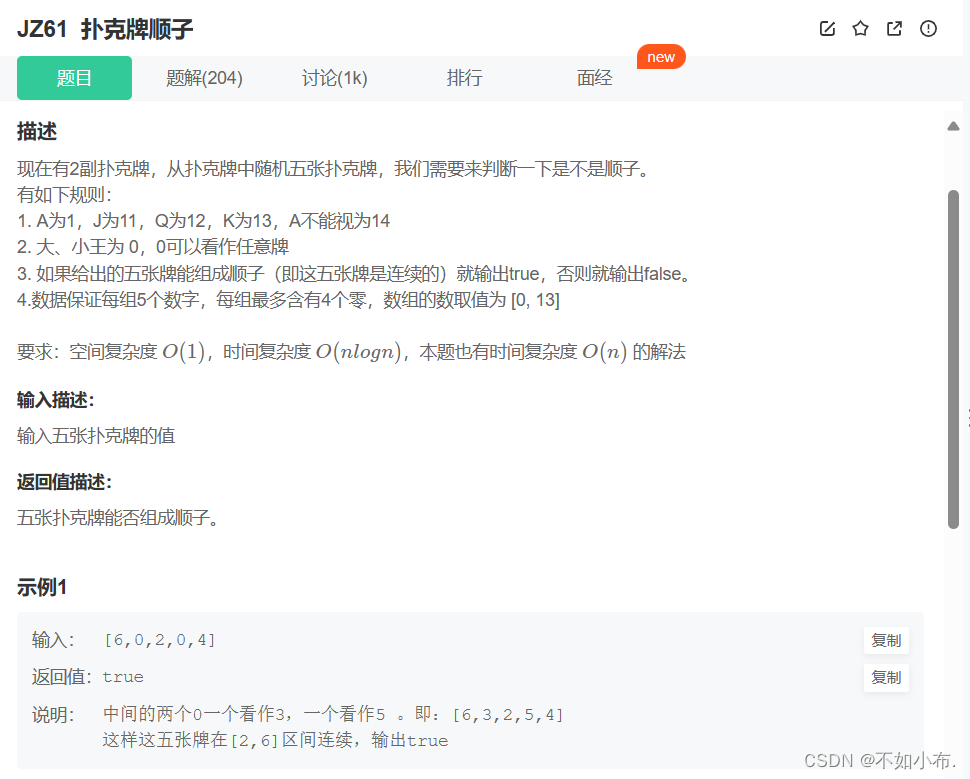
3.1 題目描述

3.2 解題思路

??一開始我想了很多，寫了半天寫不出來，最后一看題解……
??其實這道題很簡單，我們只要發現其中的規則，一下就出來了，那就是：最大的牌數和最小的牌數只差應該是等于4的（1，2，3，4，5），但是還有可能出現0的情況（3，4，5，0，0），因此所得的五張牌的最大與最小只差應該是小于等于4。 但是其中不能有重復的牌（0可以重復噢），所以還需要判斷（哈希）。
??我們只需要遍歷一遍數組，找出最大與最小，看看它們的差值是否小于等于4就可以了，同時如果出現重復數字之間返回false即可。

3.3 代碼實現

class Solution {
public:bool hash[14];bool IsContinuous(vector<int>& nums) {memset(hash, 0, sizeof hash);int maxVal = 0, minVal = 14;for(auto x : nums){if(x){if(hash[x]) return false;else{hash[x] = true;maxVal = max(maxVal, x);                minVal = min(minVal, x);                }}}return maxVal - minVal <= 4;}
};

總結

??今天的整體難度都比較簡單，沒什么可說的，大家多多練習吧。
??那么第九天的內容就到此結束了，如果大家發現有什么錯誤的地方，可以私信或者評論區指出喔。我會繼續堅持訓練的，希望能與大家共同進步！！！那么本期就到此結束，讓我們下期再見！！覺得不錯可以點個贊以示鼓勵！