以下內容來自b站up主忠厚老實的老王，視頻鏈接：自動駕駛決策規劃算法序章 總綱與大致目錄_嗶哩嗶哩_bilibili
https://www.bilibili.com/video/BV1hP4y1p7es/?spm_id_from=333.999.0.0&vd_source=d36e625f376908cfa88ef5ecf2fb0ed8侵刪。
決策規劃算法概述
數學基礎
五次多項式
?其中隱含的限制就是f(t)的定義域和值域都應該是實數，因為s和t都是真實空間中的軌跡和時間坐標，不能有虛數。
要想使得上面的那個jark最小，積分號中是平方項，也就是當其為0時最小，也就是f(t)的三階導數為0，也就是f(t)是二次或者二次以下的函數時，三階導數才為0。
?
?
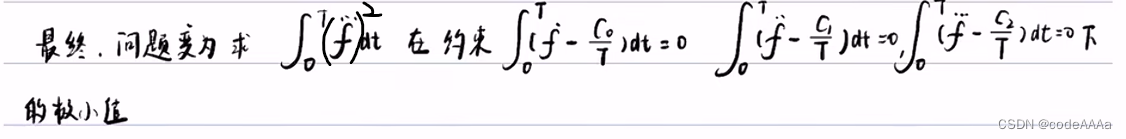
也就是求泛函
?在后面的那三個約束條件下極小值對應的f(t)。
上面把一個帶約束的泛函化成了一個無約束的泛函，但是L和f點、f兩點、f三點都有關，不能直接使用上面只能處理一階導數的歐拉——拉格朗日方程。要使用廣義的歐拉——拉格朗日方程：
?凸優化
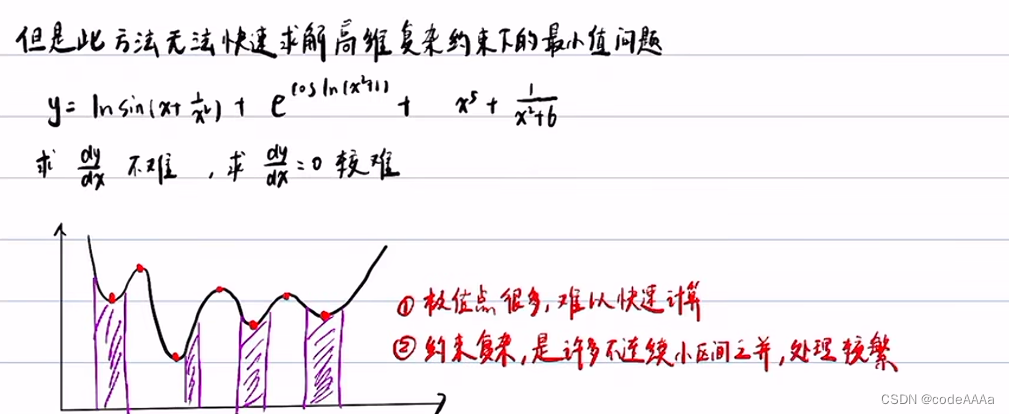
?所以一般求復雜函數在復雜約束條件下的最小值問題都采用迭代法。迭代法的求解速度要比求導法快很多。
以梯度下降法為例說明大概原理：
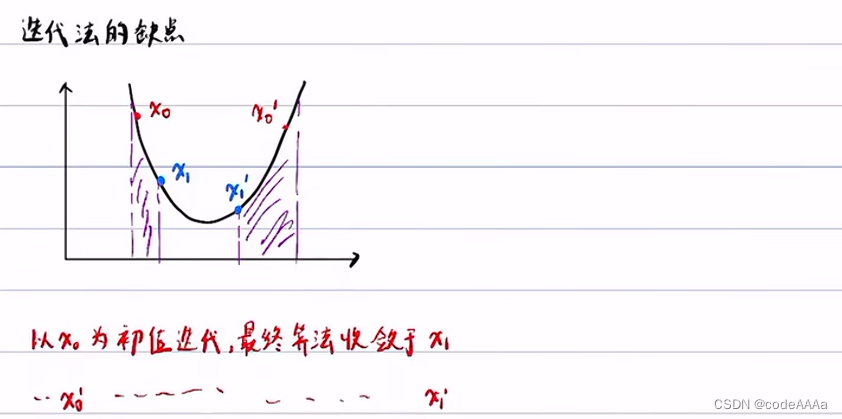
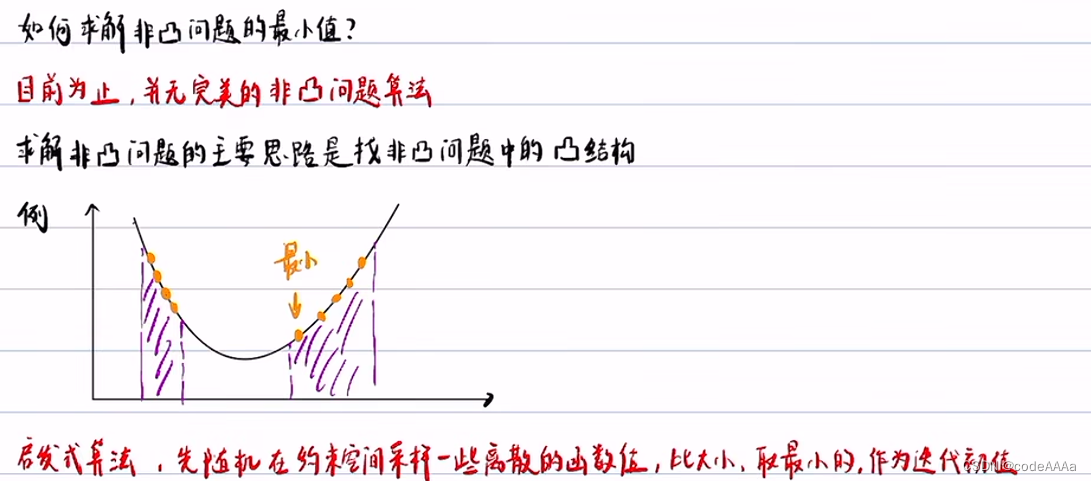
紫色區域是約束，所以迭代法對初值比較敏感，有可能收斂到局部最小值。
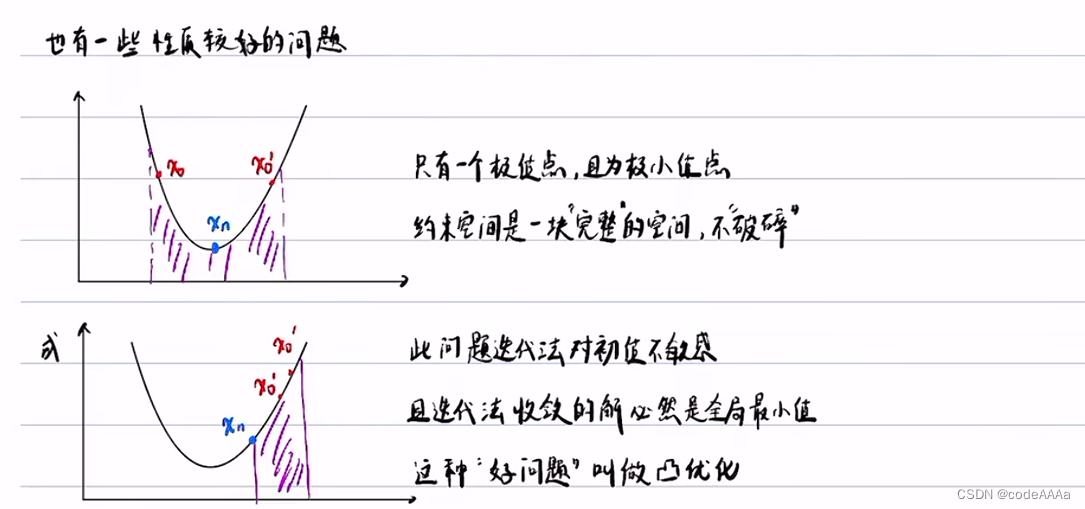
?凸優化是最簡單的非線性規劃方法。自動駕駛的規劃求解不是一個凸優化問題，凸優化必須滿cost function是一個凸函數，約束空間是一個凸空間，以避障工況為例：
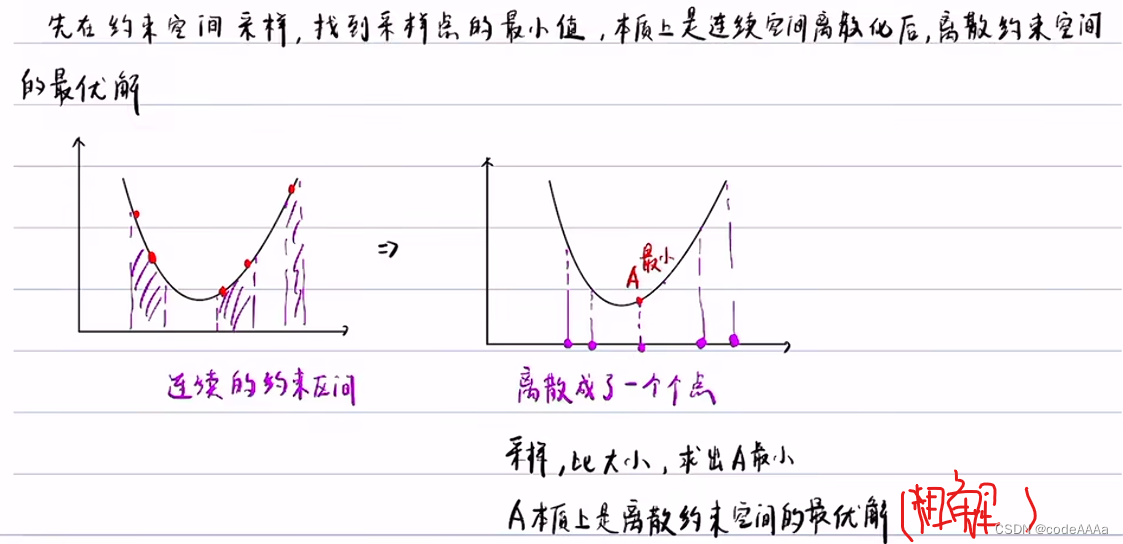
?整個過程就是：
上述方法也有一定的缺點：
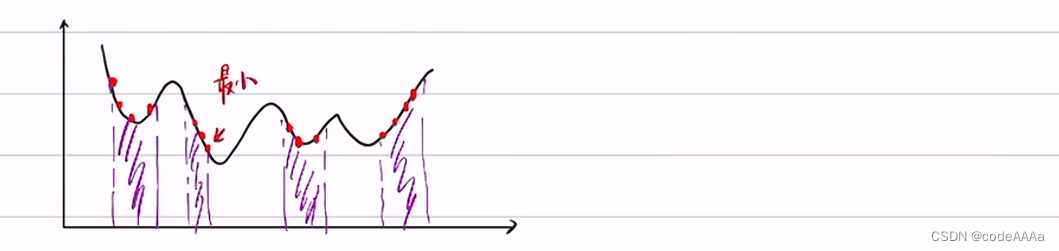
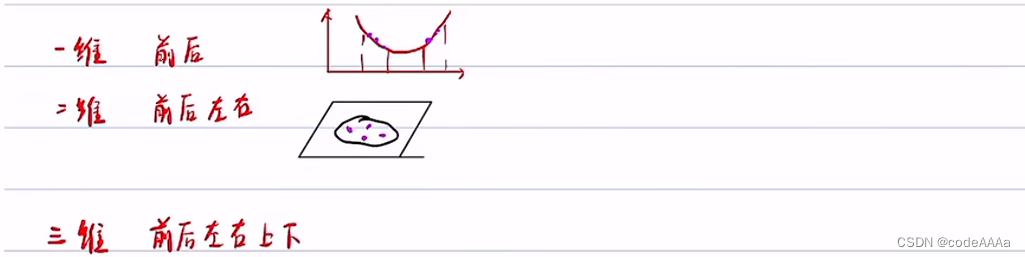
采樣點少的話會比較容易收斂到局部最優，采樣點多的話會發生維度災難，如下：
frenet坐標系和Cartesian坐標系坐標轉換
概述和基本量
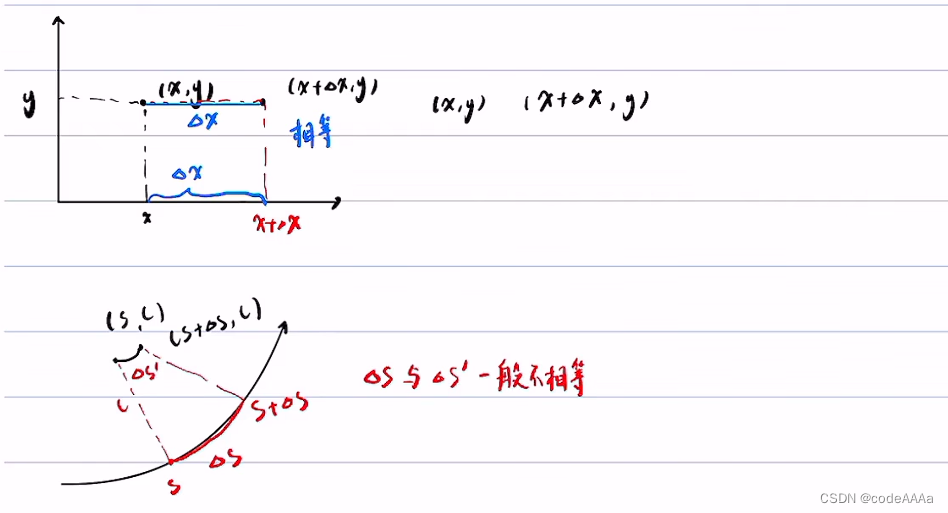
也就是在直角坐標系下想對一個函數求導，那它只有一個dx，這個dx是不區分點在x坐標上的位移還是點的實際位移在x坐標上的分量，因為這兩者一樣；但是在frenet坐標系中，它們是一樣的所以在frenet坐標系中會有d/ds和d/dsx之分。在直角坐標系中可能只有一個dx，但是在frenet坐標系中，可能會有多個ds，舉例說明如下：
這里使用dsx和ds來區分不同的s，在很多推導教程中可能中只用ds，會造成理解困難。
預備知識1
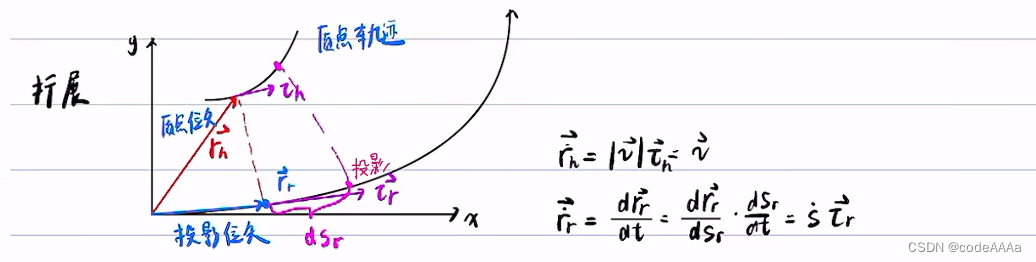
證明這個質點位矢r的導數等于v的模乘以τ，τ是質點在切線方向的單位向量。
當dt趨近于0時，ds和dr無限的接近，比值為1，方向會無限的趨近于在位矢r處的切線方向，也就是τ。
?預備知識2：frenet坐標系
其中ds是黑色曲線的弧微分，證明如下：
其中τ+dτ和τ以及dτ形成的三角形是一個等腰三角形，可以求出dτ的大小（也即使dτ的模），方向趨近于τ的法線方向。
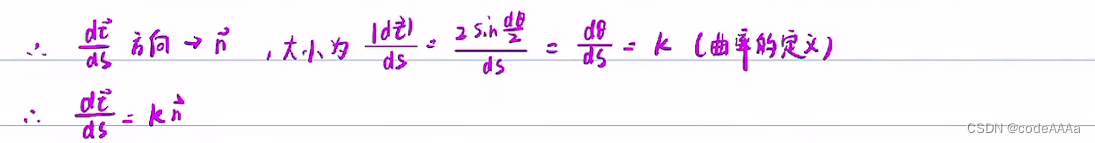其中當dτ無限趨近于0時，sin(dθ/2)等價無窮小于(dθ/2)。
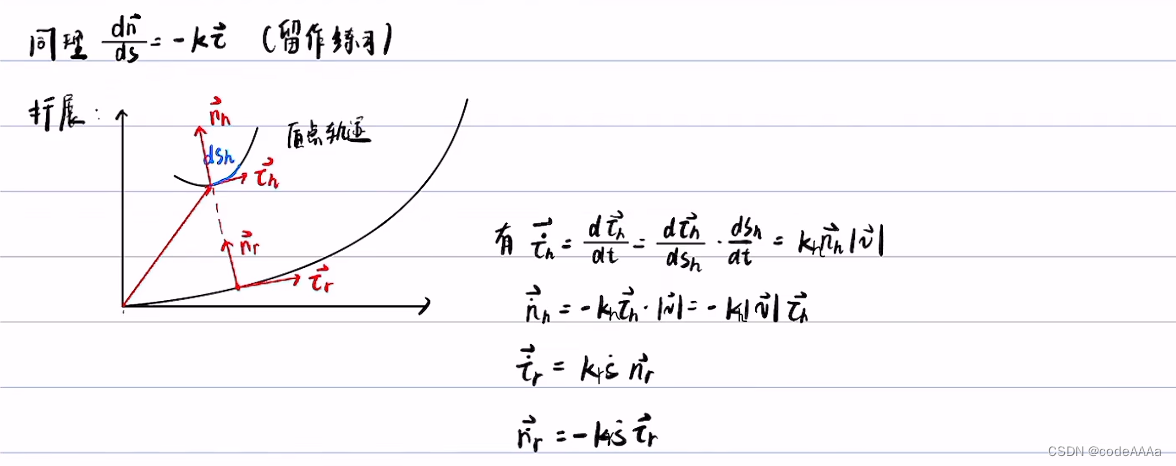
其中 kh是質點軌跡的曲率，kr是道路中心線的曲率，這里的曲率都是在直角坐標系下的曲率。
?這里的ds指的是frenet坐標軸下的弧微分。??
其中ρ是曲率半徑，法向加速度是向心加速度。
預備知識總結
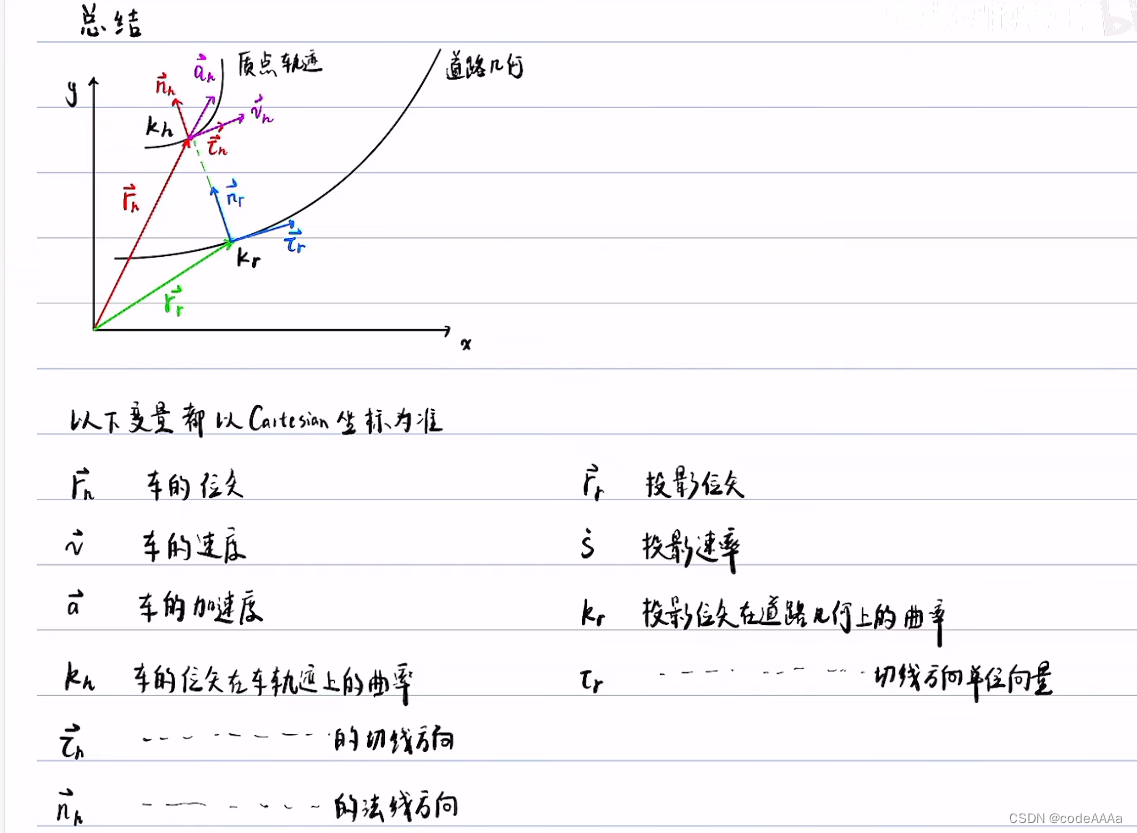
?坐標轉換(從直角坐標轉為frenet坐標）
下面的問題就是已知在笛卡爾坐標系下的
，以及frenet坐標系下的坐標起點
，算這個點在frenet坐標系下的
，其中
。
其中向量三角形是黃色區域，由向量三角形可以得到核心的公式：
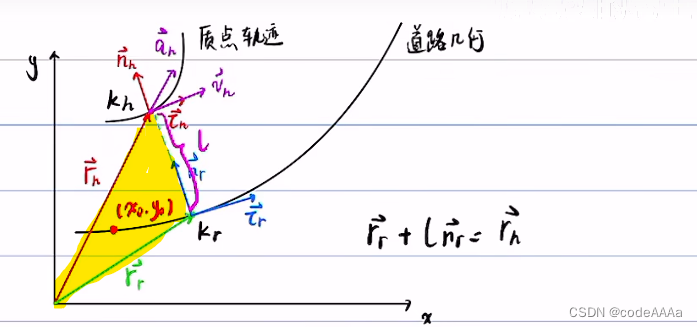
得到上面的核心公式，可以該公式和微積分依次求出，但是這個公式還不能直接使用，因為只知道rh，rr和nr未知，此時要找到投影點的相關信息。
投影點及其相關的信息的確定方法如下：
最后計算得到rr的原理如下：
為什么可以
原理如下：
?至此投影點的信息已經基本求值完畢。
?下面可以使用上面的核心公式來計算相關量。
s的計算方法是從離散規劃點起點開始把各個點的長度累加起來一直累加到投影點(xr,yr)為止。也就是以直線長度近似代替弧長：
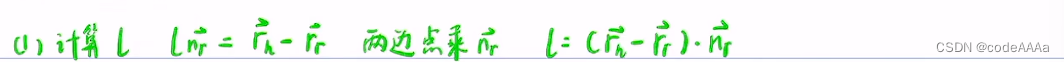
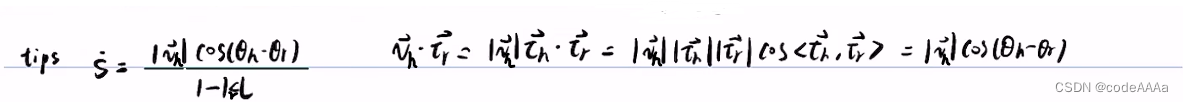
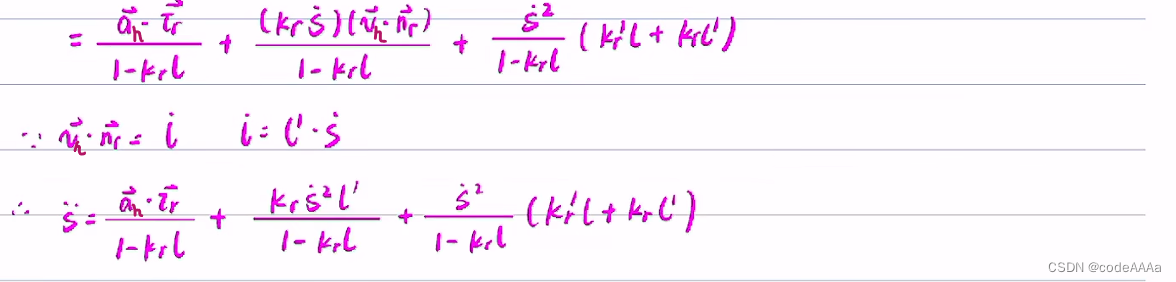
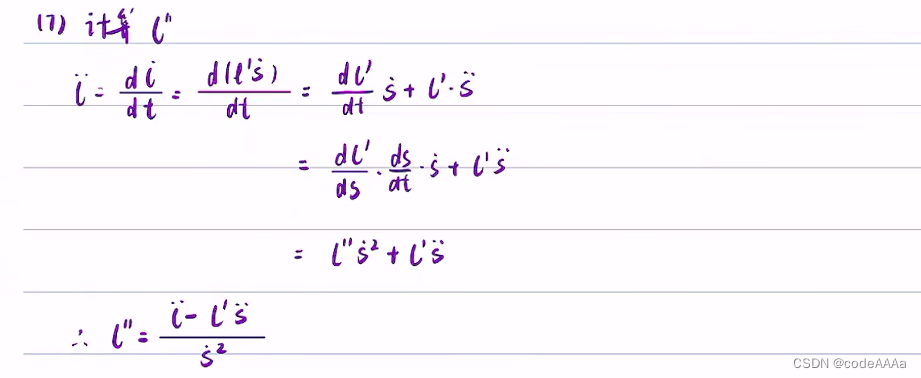
?小結
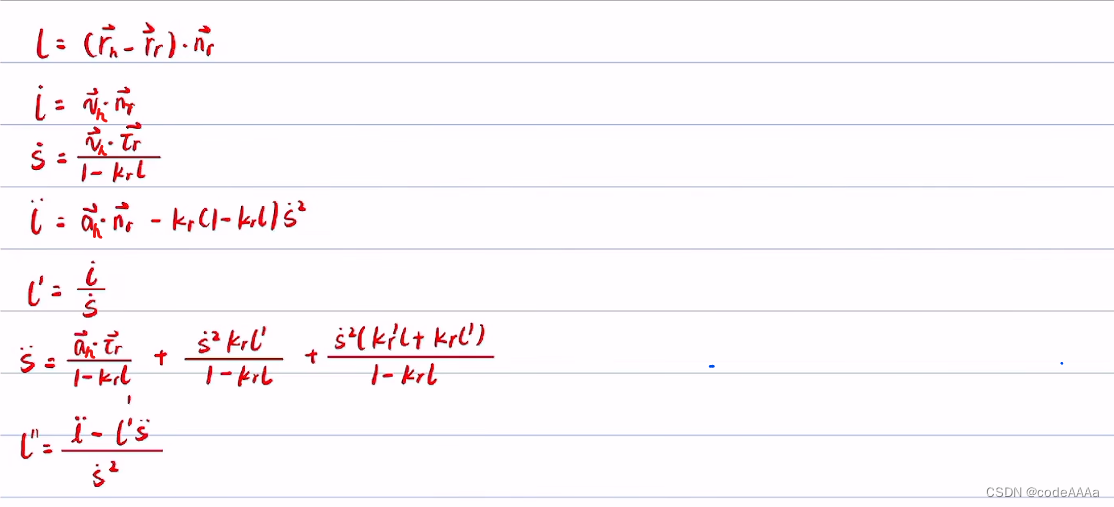
坐標變換(從frenet轉換到直角坐標)
???????
?
)
)
)
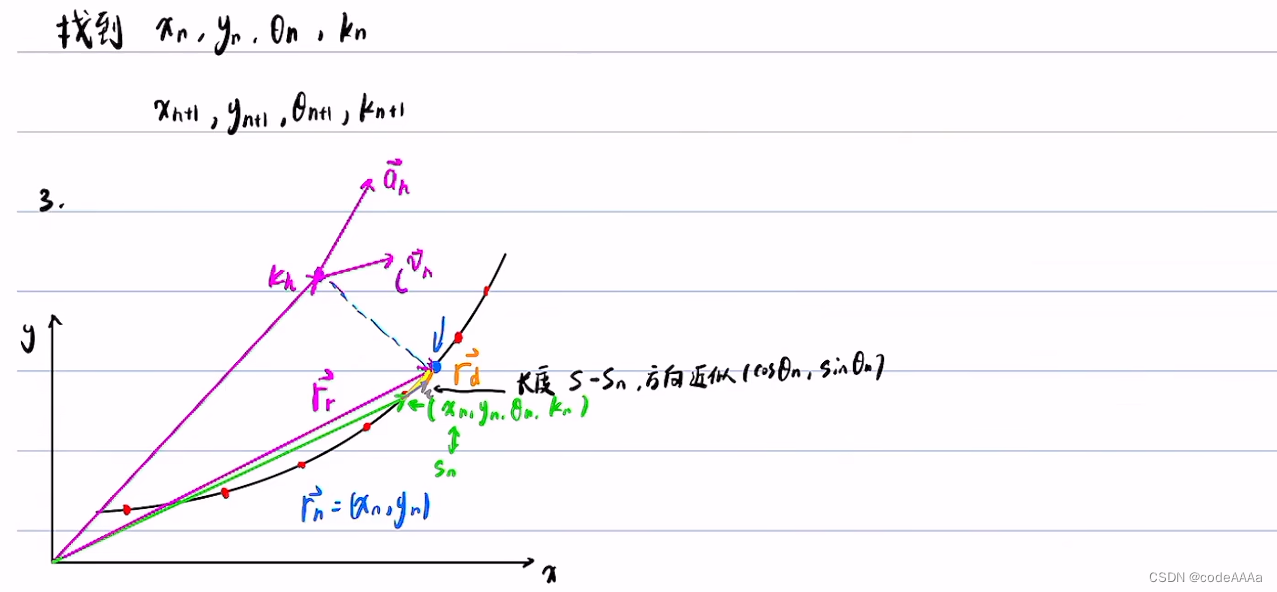
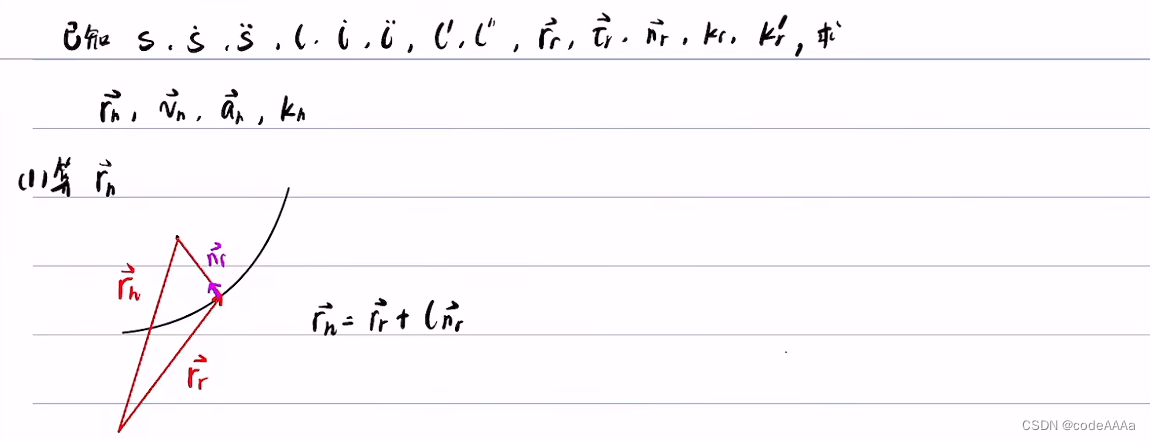
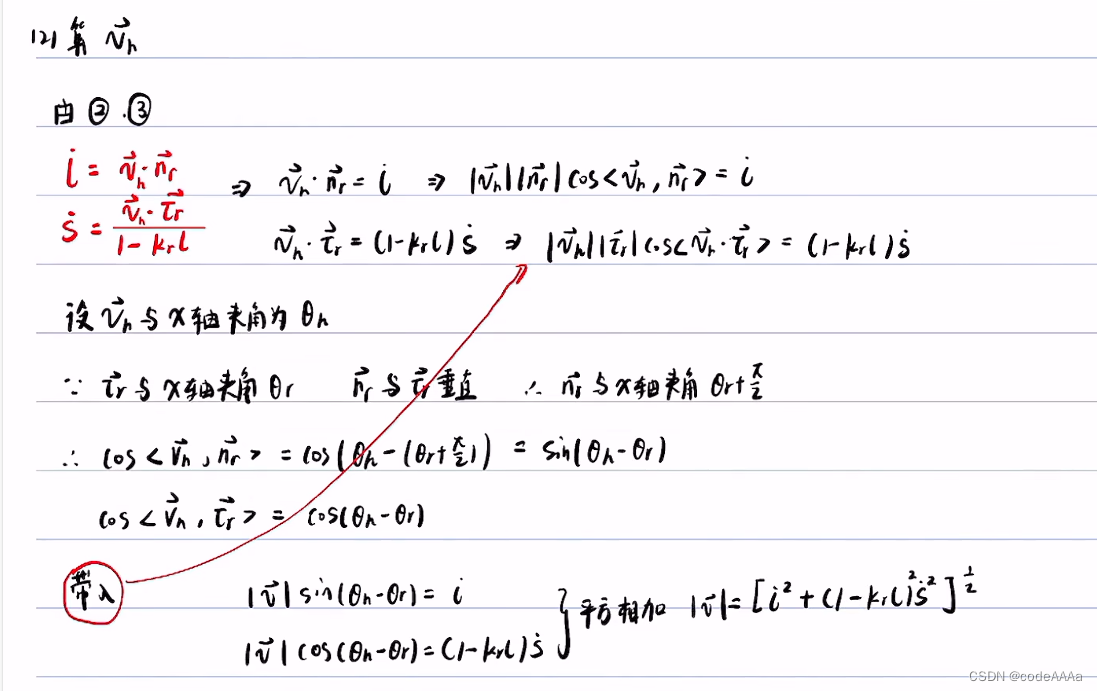
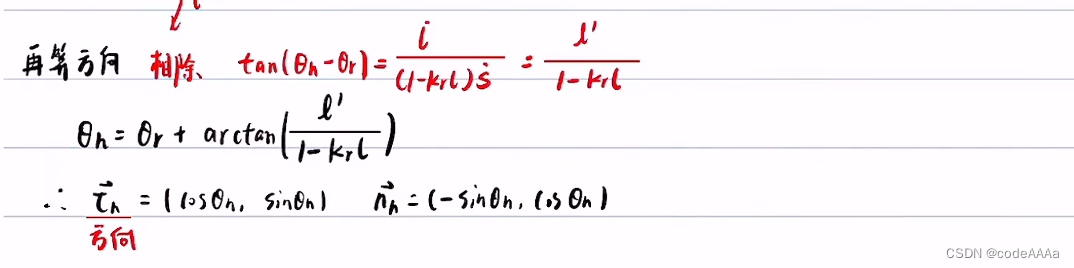
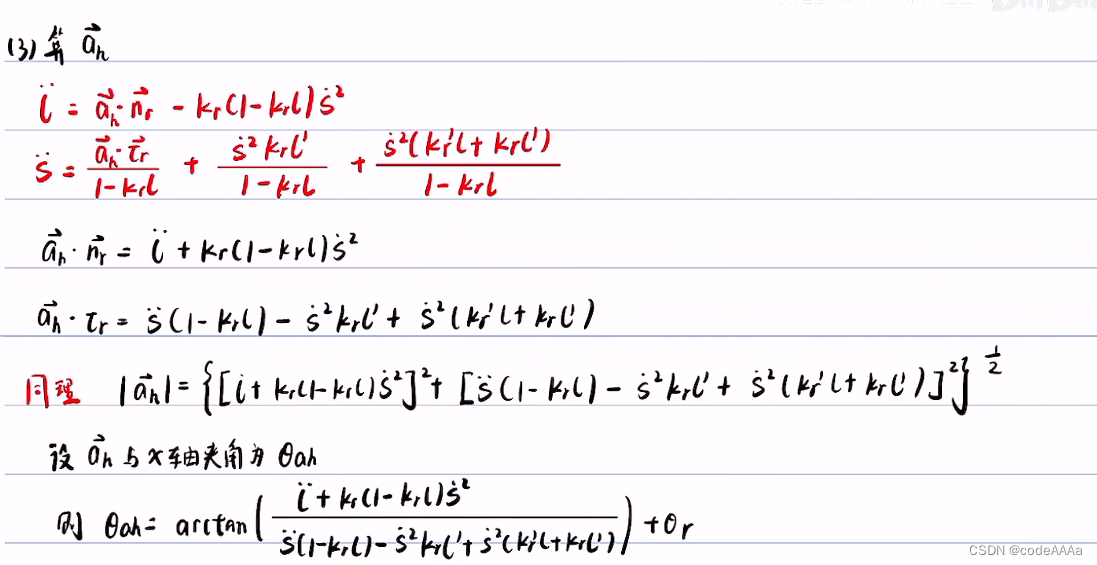
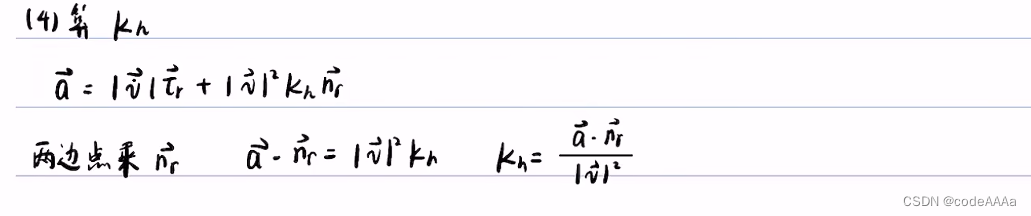
