Java數據結構—

一、樹型結構

1.1 概念

我們之前提到的數組，單鏈表，棧和隊列都是一種線性結構，每個元素都有最多一個后繼節點。而樹型結構是一種非線性結構，它是由n（n>=0）節點組成的一個具有層次關系的集合。它之所以叫做樹型結構是因為它看起來像是一棵倒掛的樹，根向上，葉子朝下。

1.2 特點

有一個特殊的結點，稱為根結點，根結點沒有前驅結點
除根結點外，其余結點被分成M(M > 0)個互不相交的集合T1、T2、……、Tm，其中每一個集合Ti (1 <= i <=m) 又是一棵與樹類似的子樹。每棵子樹的根結點有且只有一個前驅，可以有0個或多個后繼
樹是遞歸定義的，樹的子樹也滿足樹的定義

☆ 樹形結構中，子樹之間不能有交集，否則就不是樹型結構

二、樹

2.1 樹的相關概念

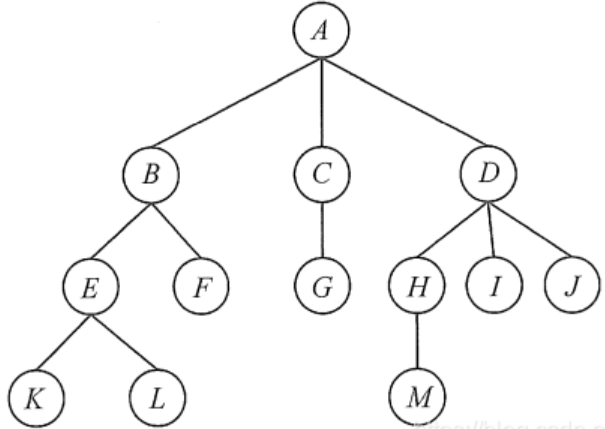
結點的度：一個結點含有子樹的個數稱為該結點的度；如上圖：A的度為3
樹的度：一棵樹中，所有結點度的最大值稱為樹的度；如上圖：樹的度為3
葉子結點或終端結點：度為0的結點稱為葉結點；如上圖：K,L,F,G,M,I,J節點為葉結點
雙親結點或父結點：若一個結點含有子結點，則這個結點稱為其子結點的父結點；如上圖：A是B的父結點,C是G的父節點
孩子結點或子結點：一個結點含有的子樹的根結點稱為該結點的子結點；如上圖：B是A的孩子結點，H是D的孩子節點
根結點：一棵樹中，沒有雙親結點的結點；如上圖：A
結點的層次：從根開始定義起，根為第1層，根的子結點為第2層，以此類推；如上圖：B節點在第二層，L節點在第四層
樹的高度或深度：樹中結點的最大層次；如上圖：樹的高度為4

樹的以下概念只需了解，在看書時只要知道是什么意思即可：

非終端結點或分支結點：度不為0的結點；如上圖：B、C、D、E...等節點為分支結點
兄弟結點：具有相同父結點的結點互稱為兄弟結點；如上圖：B、C、D是兄弟結點
堂兄弟結點：雙親在同一層的結點互為堂兄弟；如上圖：E、G互為兄弟結點
結點的祖先：從根到該結點所經分支上的所有結點；如上圖：A是所有結點的祖先
子孫：以某結點為根的子樹中任一結點都稱為該結點的子孫。如上圖：所有結點都是A的子孫
森林：由m（m>=0）棵互不相交的樹組成的集合稱為森林

2.2 樹的應用

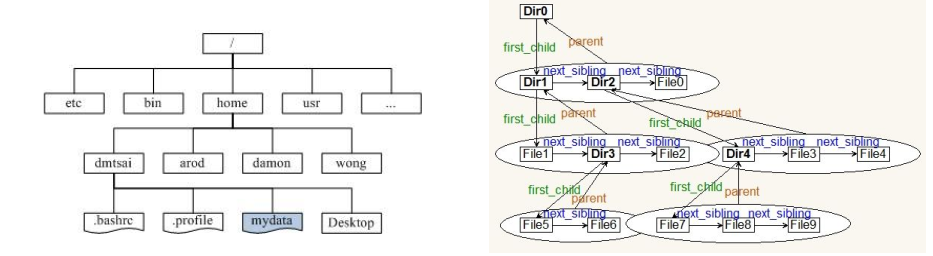
文件系統管理

三、二叉樹

3.1 二叉樹的概念

我們在樹型結構中提到，一個父節點可以有多個孩子節點，但是在二叉樹中，一個父節點最多只能有兩個孩子節點，稱為左樹和右樹

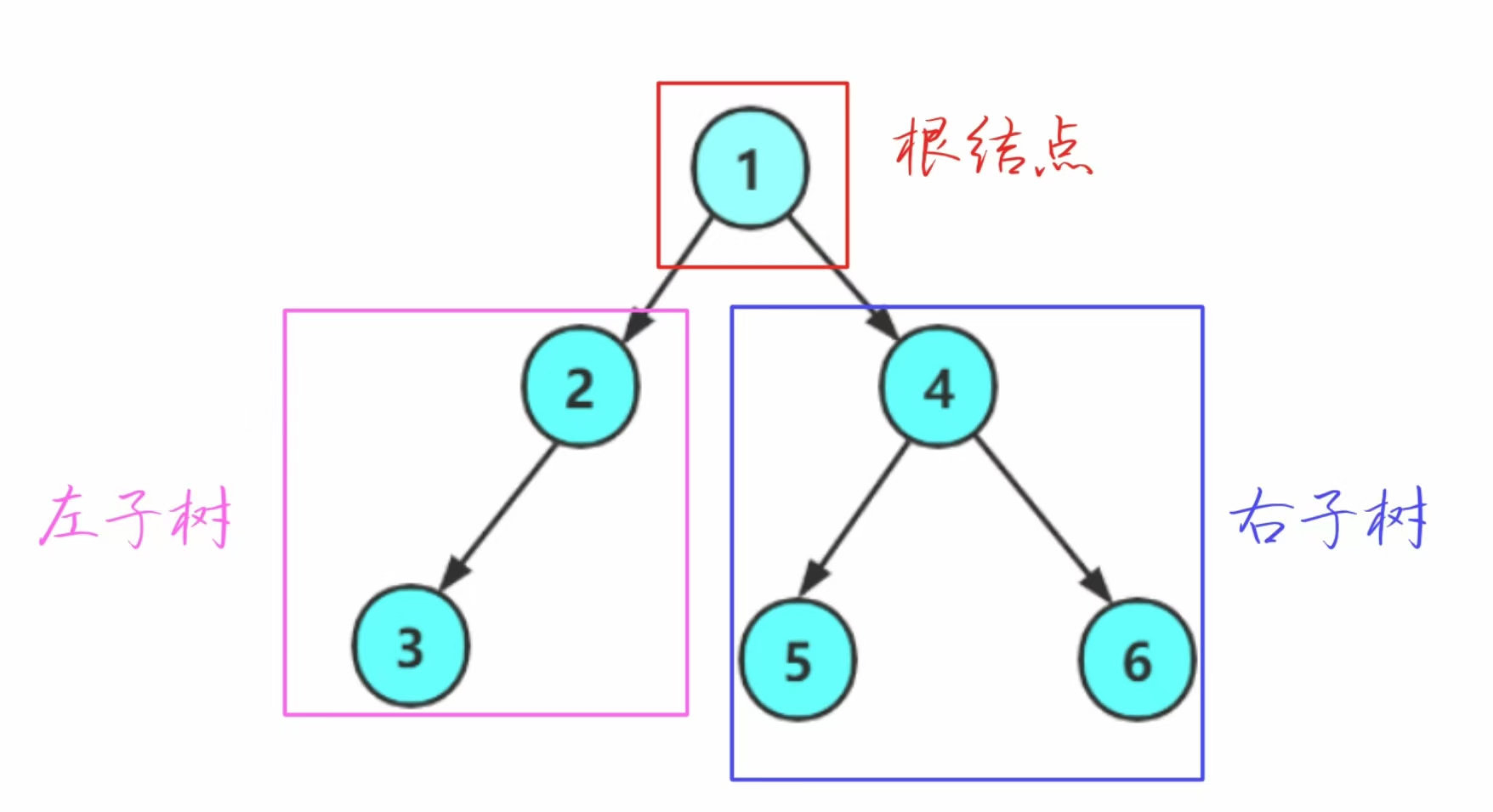
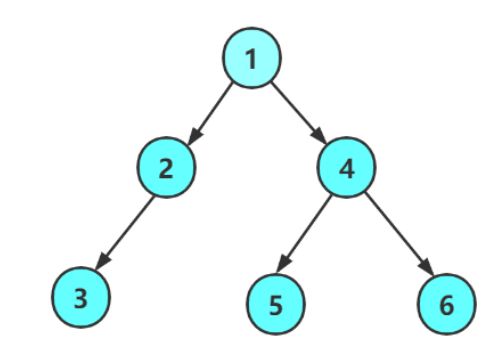
我們可以看到

二叉樹不存在度大于2的節點

二叉樹的子樹有左右之分，次序不能顛倒，因此二叉樹是有序樹

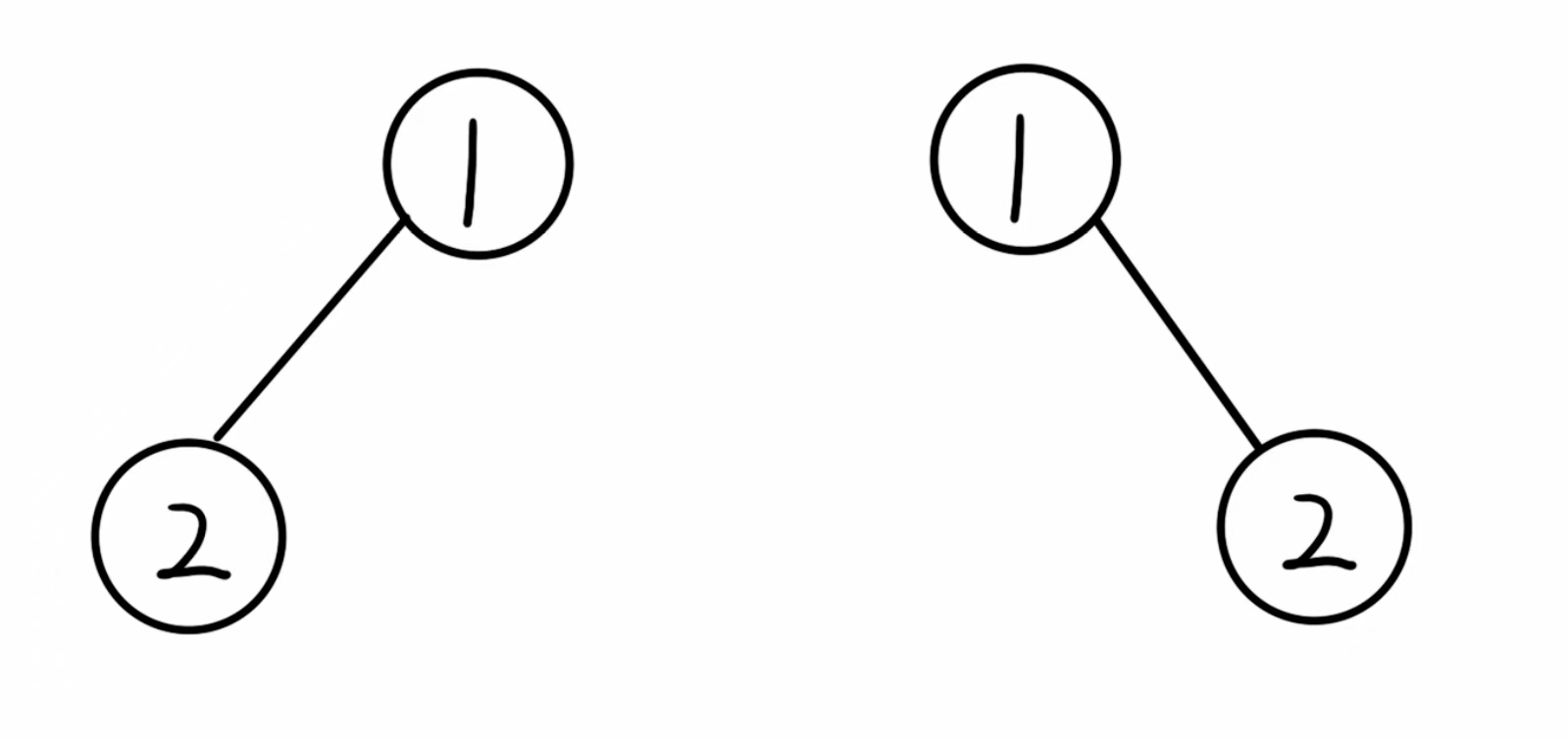
這是兩個不同的二叉樹，因為二叉樹是有序樹，所以不可以把他們看成是同一個樹

3.2 兩種特殊的二叉樹

在二叉樹根據節點不同的位置有兩種特殊的二叉樹

1.滿二叉樹：一棵二叉樹，如果每層的節點數都達到了最大值，把每個位置都填滿了，則這棵二叉樹就是滿二叉樹。在數學層面上來說，如果一棵二叉樹的層數為k，節點數為 $2^{k}$ -1，那么這棵二叉樹就是滿二叉樹

2.完全二叉樹：完全二叉樹是效率很高的數據結構，完全二叉樹是由滿二叉樹而引出來的。對于深度為k的，有n個節點的二叉樹，當且僅當每個節點斗魚深度為K的滿二叉樹中編號從0至n-1的節點一一對應時稱之為完全二叉樹

用更通俗的話去解釋完全二叉樹就是，最后一層所有的節點都要靠左，不可以有空位，最后一層上面的節點要和滿二叉樹一樣鋪滿

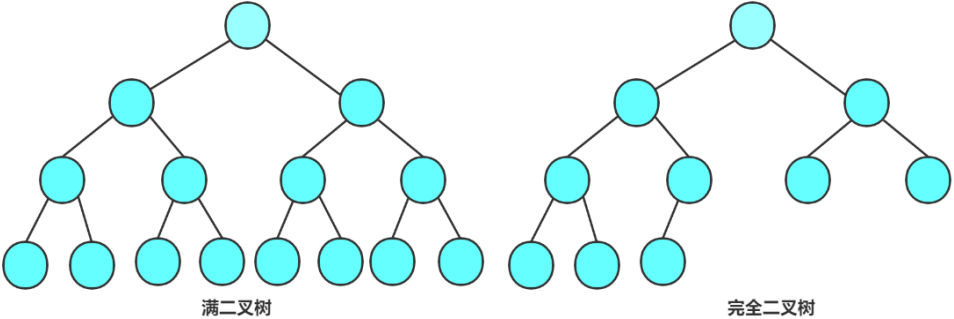
3.3 二叉樹的性質

若規定根結點的層數為1，則一棵非空二叉樹的第i層上最多有 $2^{i-1}$ (i>0)個結點
若規定只有根結點的二叉樹的深度為1，則深度為K的二叉樹的最大結點數是 $2^{k}$ -1 (k>=0)
對任何一棵二叉樹, 如果其葉結點個數為 n0, 度為2的非葉結點個數為 n2,則有n0＝n2＋1
具有n個結點的完全二叉樹的深度k為 log2(n+1)上取整
對于具有n個結點的完全二叉樹，如果按照從上至下從左至右的順序對所有節點從0開始編號，則對于序號為i的結點有：

?若i>0，雙親序號：(i-1)/2；i=0，i為根結點編號，無雙親結點
?若2i+1<n，左孩子序號：2i+1，否則無左孩子
?若2i+2<n，右孩子序號：2i+2，否則無右孩子

3.4 二叉樹的儲存

二叉樹的儲存結構分為：順序儲存和鏈式儲存

我們這里將鏈式儲存，順序儲存我們在之后的堆中會接觸到

二叉樹的鏈式儲存是通過一個一個的節點引用起來的，常見的表示方法有二叉和三叉表示方法

// 孩子表示法
class Node {int val; // 數據域Node left; // 左孩子的引用，常常代表左孩子為根的整棵左子樹Node right; // 右孩子的引用，常常代表右孩子為根的整棵右子樹
} 
// 孩子父親表示法
class Node {int val; // 數據域Node left; // 左孩子的引用，常常代表左孩子為根的整棵左子樹Node right; // 右孩子的引用，常常代表右孩子為根的整棵右子樹Node parent; // 當前節點的根節點
}

二叉表示法就是孩子表示法，節點儲存該節點的值和左孩子的地址和右孩子的地址

三叉表示法就是孩子父親表示法，節點除了儲存值和孩子的地址，還會儲存父親節點的地址

3.5 二叉樹的基本操作

3.5.1 二叉樹的前中序遍歷

前序遍歷就是先訪問根節點，再訪問根節點的左孩子，最后是根節點的右孩子。在訪問左孩子的時候依然是先訪問根節點，也就是剛剛我們提到的左孩子，再是左孩子的左孩子，最后是左孩子的右孩子。顯而易見，訪問每個節點的方法都是一樣的根左右，所以我們采用遞歸的方式進行遍歷

中序遍歷則是先訪問左孩子，再訪問根節點，最后是右孩子

后序遍歷則是先訪問左孩子，再訪問右孩子，最后是根節點

前中后序遍歷的代碼都是異曲同工，很好掌握

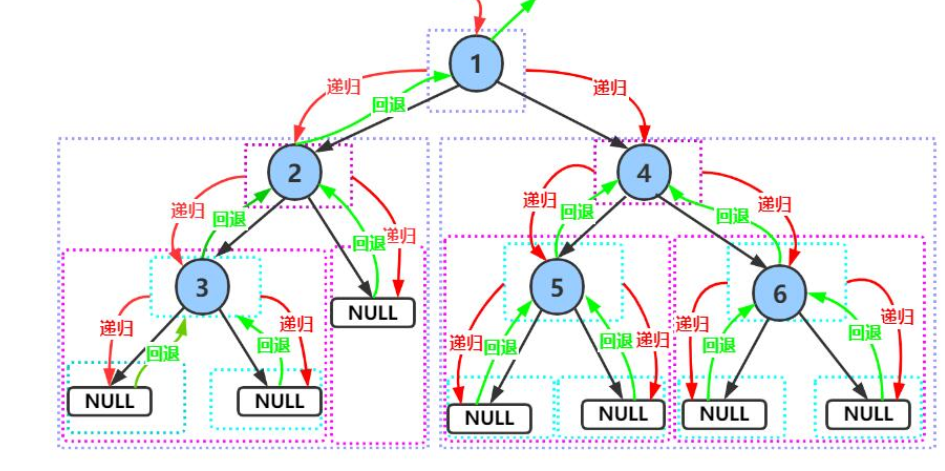
前序遍歷結構是：1 2 3 4 5 6

中序遍歷結構是：3 2 1 5 4 6

后序遍歷結構是：3 1 5 6 4 1

class Node{int val;Node left;Node right;
}
public class Test {// 前序遍歷void preOrder(Node root){if(root==null) return;System.out.println(root.val);preOrder(root.left);preOrder(root.right);}// 中序遍歷void inOrder(Node root){if(root==null) return;inOrder(root.left);System.out.println(root.val);inOrder(root.right);}// 后序遍歷void postOrder(Node root){if(root==null) return;postOrder(root.left);postOrder(root.right);System.out.println(root.val);}}

3.5.2 二叉樹的層序遍歷

層序遍歷就是從第一層開始，從左到右，從上到下依次訪問節點，我們采用隊列來實現層序遍歷。先在隊列中加入根節點，然后進入循環，只要隊列不為空就先刪除隊頭節點并保存，再打印隊頭節點的值，之后加入該節點的左孩子和右孩子

   public void levelOrder(TreeNode root) {if(root == null) {return;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode cur = queue.poll();System.out.print(cur.val+" ");if(cur.left != null) {queue.offer(cur.left);}if(cur.right != null) {queue.offer(cur.right);}}}

3.5.3 二叉樹的常用操作

    //獲取當前二叉樹的節點個數public int getNodeSize2(TreeNode root) {if(root == null) return 0;return getNodeSize2(root.left) +getNodeSize2(root.right) + 1;}//獲取葉子節點的個數public int getLeafNodeCount2(TreeNode root) {if(root == null) {return 0;}if(root.left == null && root.right == null) {return 1;}return getLeafNodeCount2(root.left) +getLeafNodeCount2(root.right);}//第K層節點的個數public int getKLevelNodeCount(TreeNode root,int k) {if(root == null) {return 0;}if(k == 1) {return 1;}return getKLevelNodeCount(root.left,k-1) +getKLevelNodeCount(root.right,k-1);}//二叉樹的高度public int getHeight(TreeNode root) {if(root == null) return 0;int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);return Math.max(leftHeight,rightHeight) + 1;}//查找是否有key值的節點public TreeNode find(TreeNode root,char key) {if(root == null) {return null;}if(root.val == key) {return root;}TreeNode leftResult = find(root.left,key);if(leftResult != null) {return leftResult;}TreeNode rightResult = find(root.right,key);if(rightResult != null) {return rightResult;}return null;}//判斷樹是否為完全二叉樹public boolean isCompleteTree(TreeNode root) {if(root == null) return true;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode cur = queue.poll();if(cur != null) {queue.offer(cur.left);queue.offer(cur.right);}else {break;}}while (!queue.isEmpty()) {TreeNode cur = queue.peek();if(cur == null) {queue.poll();}else {return false;}}return true;}