本文給大家帶來的百面算法工程師是正則優化函數，文章內總結了常見的提問問題，旨在為廣大學子模擬出更貼合實際的面試問答場景。在這篇文章中，我們將總結一些BN、LN、Dropout的相關知識，并提供參考的回答及其理論基礎，以幫助求職者更好地準備面試。通過對這些問題的理解和回答，求職者可以展現出自己的算法領域的專業知識、解決問題的能力以及對實際應用場景的理解。同時，這也是為了幫助求職者更好地應對深度學習目標檢測崗位的面試挑戰，提升面試的成功率和競爭力。

目錄

17.1 什么是過擬合和欠擬合

17.2 解決過擬合和欠擬合的方法有哪些

17.3 什么是正則化？

17.4 L1與L2為什么對于特征選擇有著不同方式

17.5 正則化有什么作用

17.6 介紹一下BN

17.7 BN訓練與測試有什么不同

17.8 BN/LN/IN/GN區別

---

?歡迎大家訂閱我的專欄一起學習共同進步

祝大家早日拿到offer！ let's go

百面算法工程師專欄：🚀🚀🚀http://t.csdnimg.cn/dfcH3🚀🚀🚀點擊即可跳轉

17.1 什么是過擬合和欠擬合

過擬合和欠擬合是指機器學習模型在訓練過程中的兩種常見問題。

1. 過擬合（Overfitting）：過擬合指的是模型在訓練數據上表現得太好，以至于無法很好地泛化到新的、未見過的數據上。這種情況下，模型可能過度地記住了訓練數據的細節和噪聲，而沒有學到數據背后的真正規律。過擬合的模型通常在訓練集上表現很好，但在測試集或實際應用中表現不佳。
2. 欠擬合（Underfitting）：欠擬合指的是模型在訓練數據上表現得不夠好，無法捕捉到數據中的真實關系。這種情況下，模型可能過于簡單，沒有足夠的能力來擬合數據的復雜性和變化。欠擬合的模型通常在訓練集和測試集上表現都不太好。

17.2 解決過擬合和欠擬合的方法有哪些

解決過擬合和欠擬合的方法包括：

• 過擬合：減少模型復雜度（如減少參數數量、增加正則化項）、增加訓練數據、使用更簡單的模型、數據增強、擴充數據集等。
• 欠擬合：增加模型復雜度（如增加參數數量、增加層級）、優化模型架構、增加特征數量或改進特征工程等。

通過調整模型的復雜度、增加數據量、優化超參數等方法，可以有效地解決過擬合和欠擬合問題，使模型在訓練集和測試集上都表現良好，并能夠泛化到新的數據上。

17.3 什么是正則化？

正則化是一種用于減少模型過擬合的技術，通過向模型的損失函數中添加額外的懲罰項來控制模型的復雜度。正則化的目標是限制模型的參數大小，防止模型過度擬合訓練數據，從而提高模型在未見過的數據上的泛化能力。

在機器學習中，常見的正則化方法包括：

1. L1 正則化（Lasso 正則化）：向損失函數添加 L1 范數懲罰項，即模型參數的絕對值之和。這使得一些不重要的特征的系數趨向于零，從而實現特征選擇的效果，使模型更加稀疏。
2. L2 正則化（Ridge 正則化）：向損失函數添加 L2 范數懲罰項，即模型參數的平方和。L2 正則化傾向于使所有參數都很小但非零，對模型的影響是均衡的。
3. ElasticNet 正則化：同時結合了 L1 和 L2 正則化，通過兩種懲罰項來控制模型的復雜度。

正則化的選擇通常基于實際問題的復雜度和數據集的特點。適當的正則化可以幫助防止過擬合，提高模型的泛化能力，但需要在正則化項的權衡下進行調整，以避免欠擬合。

17.4 L1與L2為什么對于特征選擇有著不同方式

L1范數和L2范數在正則化過程中對特征選擇產生不同方式的影響，這是因為它們在懲罰項的計算方式上有所不同。

1. L1 正則化（Lasso 正則化）：

1. 正則化的懲罰項是模型參數的絕對值之和。由于 范數具有稀疏性，即很多參數的取值會被壓縮到零，因此 正則化有助于進行特征選擇。當使用 正則化時，模型傾向于使一些不重要的特征的系數趨向于零，從而實現了自動特征選擇的效果。這樣可以減少模型的維度，提高了模型的解釋性和計算效率。

1. L2 正則化（Ridge 正則化）：

1. 正則化的懲罰項是模型參數的平方和。相比于 L1 正則化， 正則化對所有參數的影響是均衡的，不會將參數完全壓縮到零。雖然 正則化也可以幫助減少過擬合，但它不像 L1 正則化那樣能夠直接實現特征選擇。在 正則化下，模型會傾向于使所有特征都有一定的影響，而不會將某些特征的系數壓縮到零。

因此，L1 正則化在特征選擇方面更為強大，而 L2 正則化更適用于減少過擬合并提高模型的泛化能力。在實際應用中，選擇合適的正則化方法需要根據具體問題的特點以及模型的需求來進行權衡。

17.5 正則化有什么作用

正則化在機器學習中有幾個重要的作用：

1. 防止過擬合：過擬合是指模型在訓練數據上表現得過好，但在未見過的新數據上表現不佳的問題。正則化通過向模型的損失函數中添加額外的懲罰項，限制了模型的復雜度，從而減少了模型對訓練數據中噪聲和細節的過度擬合，提高了模型在未見過的數據上的泛化能力。
2. 特征選擇：在 L1 正則化中，由于懲罰項會將一些不重要的特征的系數推向零，因此可以實現自動特征選擇的效果。這樣可以減少模型的維度，提高了模型的解釋性和計算效率。
3. 降低模型復雜度：正則化通過控制模型參數的大小，有效地降低了模型的復雜度。這對于防止模型過度擬合和提高模型的穩定性非常重要，尤其是在數據量較少或者特征維度較高的情況下。
4. 提高泛化能力：正則化可以幫助模型更好地泛化到未見過的數據上。通過控制模型的復雜度，使其更加平滑和穩定，從而提高了模型的泛化能力，使其能夠更好地適應新的、未見過的數據。

17.6 介紹一下BN

批量歸一化（Batch Normalization，簡稱BN）是一種用于加速深度神經網絡訓練并提高模型性能的技術。它在神經網絡的每一層中對輸入數據進行歸一化處理，使得每一層的輸入保持在一個相對穩定的分布上。

批量歸一化的主要思想是將每一層的輸入數據進行歸一化處理，使其均值接近于0，標準差接近于1。這有助于緩解了深度神經網絡中的內部協變量偏移問題，即每一層輸入數據的分布隨著網絡參數的更新而發生變化，導致訓練過程變得不穩定。通過批量歸一化，可以使得每一層的輸入數據都保持在一個穩定的分布上，有利于網絡的訓練和收斂。

批量歸一化的操作通常包括以下幾個步驟：

1. 對每一個mini-batch中的數據進行歸一化處理，即將每個特征的值減去該特征在該mini-batch中的均值，然后除以該特征在該mini-batch中的標準差。
2. 對歸一化后的數據進行線性變換，即將每個特征乘以一個學習參數（縮放參數），然后再加上另一個學習參數（平移參數）。
3. 可選地，可以引入一個激活函數對變換后的數據進行非線性處理。

批量歸一化的優點包括：

• 加速模型訓練：通過緩解深度神經網絡中的內部協變量偏移問題，加速了模型的訓練過程，使得網絡更容易收斂。
• 提高模型性能：批量歸一化使得網絡更加穩定，能夠更快地收斂到更好的局部最優解，從而提高了模型的性能和泛化能力。
• 減少對參數初始化的依賴：批量歸一化可以緩解對參數初始化的依賴，使得網絡對參數初始化的選擇更加魯棒。

然而，批量歸一化也有一些缺點，包括：

• 計算代價：批量歸一化需要在每一個mini-batch中對數據進行歸一化處理，增加了一定的計算代價。
• 不適用于小批量訓練：在小批量訓練的情況下，由于每個mini-batch中的樣本數量較少，計算得到的均值和標準差可能不夠準確，導致歸一化效果不佳。

綜上所述，批量歸一化是一種有效的深度神經網絡正則化方法，能夠加速模型訓練并提高模型性能，但在實際應用中需要根據具體情況權衡其優缺點。

17.7 BN訓練與測試有什么不同

在批量歸一化（Batch Normalization，簡稱BN）的訓練和測試階段，存在一些不同之處：

1. 訓練階段：
   • 在訓練階段，批量歸一化會根據每個mini-batch的數據計算均值和標準差，并使用這些統計量對當前的mini-batch進行歸一化處理。
   • 在訓練過程中，批量歸一化會利用mini-batch中的數據來計算均值和標準差，因此每個mini-batch的均值和標準差都可能會有所不同。
   • 訓練時，批量歸一化會記錄每一層的歸一化所需的均值和標準差，這些均值和標準差會在測試階段用于歸一化測試數據。
2. 測試階段：
   • 在測試階段，由于測試數據不再分為mini-batch，因此無法計算mini-batch的均值和標準差。
   • 因此，測試階段會使用在訓練階段計算得到的每一層的均值和標準差來進行歸一化處理。
   • 在測試過程中，批量歸一化使用訓練階段保存的均值和標準差對整個測試集進行歸一化處理，而不是使用每個mini-batch的均值和標準差。

總結起來，批量歸一化在訓練階段和測試階段的主要區別在于歸一化所使用的統計量不同。在訓練階段，根據每個mini-batch的數據計算均值和標準差進行歸一化，而在測試階段則使用訓練階段計算得到的每一層的均值和標準差對整個測試集進行歸一化。

更詳細的內容可以參考李宏毅老師的講解?

17.8 BN/LN/IN/GN區別

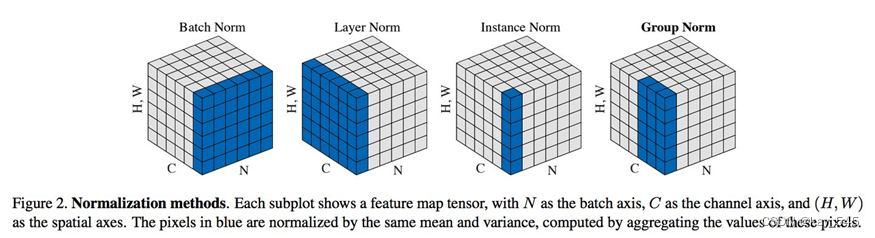
下面是關于批量歸一化（BN）、層歸一化（LN）、實例歸一化（IN）和組歸一化（GN）的區別：

歸一化方法	訓練階段統計量	歸一化對象	適用范圍	實現方式
BN	每個mini-batch	每一層的輸入數據	批量數據（mini-batch）	參數化
LN	整個樣本集	每一層的輸入數據	每一層的所有樣本	參數化
IN	每個樣本	每一層的輸入數據	每一層的每一個樣本	參數化
GN	每個組	每一層的輸入數據	每一層的特定分組	非參數化

• 訓練階段統計量：在訓練階段用于歸一化的統計量。BN使用每個mini-batch的均值和標準差，LN使用整個樣本集的均值和標準差，IN使用每個樣本的均值和標準差，而GN則使用每個組（group）的均值和標準差。
• 歸一化對象：每一層的輸入數據進行歸一化的對象。BN、LN、IN和GN都是對每一層的輸入數據進行歸一化處理，但歸一化的對象不同。
• 適用范圍：歸一化方法適用的數據范圍。BN適用于批量數據（mini-batch），LN適用于每一層的所有樣本，IN適用于每一層的每一個樣本，而GN適用于每一層的特定分組。
• 實現方式：歸一化方法的實現方式。BN、LN和IN都是參數化的，即歸一化操作會受到訓練過程中學習到的參數的影響，而GN則是非參數化的，不會學習到額外的參數。