貝葉斯分類器詳解

?1 概率論知識

1.1 先驗概率

先驗概率是基于背景常識或者歷史數據的統計得出的預判概率，一般只包含一個變量，例如P(A)，P(B)。

1.2 聯合概率

聯合概率指的是事件同時發生的概率，例如現在A,B兩個事件同時發生的概率，記為P(A,B)、P(A∩B)、P(AB)。

若事件A和事件B相互獨立，則有：

$P(A,B)=P(A)P(B)$

例子：假設事件A為明天上班，事件B為明天中彩票，其中P(A)=0.5，P(B)=0.5，則明天既上班又中彩票的概率為P(A)P(B)=0.25

1.3 條件概率

其中一般條件概率中的A事件表示結果，B事件表示原因，即由因求果

其中，P (AB) 就是聯合概率。在A與B相互獨立的情況下，易得:

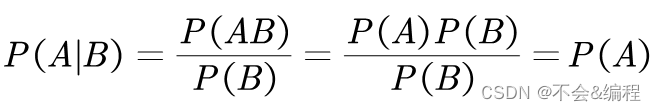
即B事件對A事件沒有影響

1.4 后驗概率

后驗概率和條件概率的區別是：后驗概率是由果求因：，例如，事件A是由事件B引起的，則P(A|B)是條件概率，P(B|A)是后驗概率

舉個通俗易懂的例子：

條件概率：新聞說今天路上出現了交通事故，若想推算一下因此而堵車的概率，也就是 P(堵車|交通事故)，這是由因推果。
后驗概率：出門后路上遇到了堵車，若想推算一下這次堵車是由發生了交通事故而引起的概率，也就是后驗概率 P(交通事故|堵車)，這是由果求因。

1.5 全概率公式

（1）樣本空間

（2）全概率公式

1.6 貝葉斯公式

設樣本空間為Ω，B為Ω中的事件， $A_{1},A_{2},\cdots ,A_{n}$ 為Ω的一個劃分，且 $P(B) > 0, P(A_{i})>0,i = 1,2,\cdots,n$ ，則有：

$P(A_{i}|B)=\frac{P(B|A_{i})P(A_{i})}{\sum_{j=1}^{n} P(B|A_{j})P(A_{j})}, i=1,2,\cdots,n$

稱上式為貝葉斯公式，也稱為逆概率公式

2 貝葉斯分類器理論知識

2.1 樸素貝葉斯發的學習與分類

2.1.1?基本方法

設

輸入空間： $\chi$ ? $\subseteq$ ? $\mathbb{R}^{n}$ 為n維集合的向量
輸出空間：類標記集合 $\Upsilon =$ ? $\begin{Bmatrix} c_{1},c_{2},\cdots,c_{k} \end{Bmatrix}$
輸入為特征向量： $x \in$ ? $\chi$
輸出為類標記（class label）： $y \in$ ? $\Upsilon$

X是定義在輸入空間 $\chi$ 上的隨機向量，Y是定義在輸出空間 $\Upsilon$ 上的隨機變量。 $P(X,Y)$ 是X和Y的聯合概率分布。訓練數據集

? $T=\begin{Bmatrix} \begin{pmatrix} x_{1},y_{1} \end{pmatrix}, \begin{pmatrix} x_{2},y_{2} \end{pmatrix},\cdots,\begin{pmatrix} x_{N},y_{N} \end{pmatrix} \end{Bmatrix}$

是 $P(X,Y)$ 獨立同分布產生

樸素貝葉斯法通過訓練數據集學習聯合概率分布 $P(X,Y)$ ,學習過程如下：

（1）學習先驗概率分布及條件概率分布

先驗概率分布： $P(Y=c_{k}),k=1,2,\cdots,K$
條件概率分布： $\mbox{$P(X=x|Y=c_{k})=P(X^{(1)}=x^{(1)},\cdots,X^{(n)}=x^{(n)}|Y=c_{k}), k=1,2,\cdots,K$}$

假設 $x^{(j)}$ 可取值有 $S_{j}$ 個， $j=1,2,\cdots,n$ ,Y的可能取值有K個，那么參數的個數有 $K\prod_{j=1}^{n}S_{j}$ ，因此條件概率分布 $P(X=x|Y=c_{k})$ 有指數級別數量的參數，其估計實際是不可行的

樸素貝葉斯法對條件概率分布作了條件獨立性的假設。由于這是一個較強的假設，樸素貝葉斯法也由此得名。樸素貝葉斯法的條件獨立性假設為：

$\mbox{$P(X=x|Y=c_{k})=P(X^{(1)}=x^{(1)},\cdots,X^{(n)}=x^{(n)}|Y=c_{k})=\prod_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_{k}) ~~~(1)$}$

樸素貝葉斯法實際上學習到生成數據的機制，所以屬于生成模型。條件獨立假設等于是說用于分類的特征在類確定的條件下都是條件獨立的。這一假設使樸素貝葉斯法變得簡單，但有時會犧牲一定的分類準確率。

樸素貝葉斯分類時，對給定的輸入x，通過學習到的模型計算后驗概率分布 $P(X=x|Y=c_{k})$ ，將后驗概率最大的類作為x的類輸出，后驗概率計算根據貝葉斯定理進行：

$\mbox{$P(Y=c_{k}|X=x) = \frac{P(X=x|Y=c_{k})P(Y=c_{k})}{\sum_{k}P(X=x|Y=c_{k})P(Y=c_{k})}~~~(2)$}$

將公式（1）代入到公式（2）可得：

$\mbox{$P(Y=c_{k}|X=x) = \frac{P(Y=c_{k})\prod_{j}P(X^{(j)}=x^{(j)}|Y=c_{k})}{\sum_{k}P(Y=c_{k})\prod_{j}P(X^{(j)}=x^{(j)}|Y=c_{k})}~k=1,2,\cdots,K~~~(3)$}$

于是，樸素貝葉斯分類器可表示為：

$\mbox{$y=f(x)=argmax_{c_{k}}P(Y=c_{k}|X=x) = \frac{P(Y=c_{k})\prod_{j}P(X^{(j)}=x^{(j)}|Y=c_{k})}{\sum_{k}P(Y=c_{k})\prod_{j}P(X^{(j)}=x^{(j)}|Y=c_{k})}~~~(4)$}$

由于分母是一樣的，所以可以簡化為：

$\mbox{$y=f(x)=argmax_{c_{k}}P(Y=c_{k})\prod_{j}P(X^{(j)}=x^{(j)}|Y=c_{k})~~~(5)$}$

2.1.2 后驗概率最大化含義

樸素貝葉斯會將實例分到后驗概率最大的類中，即等價于期望風險最小化，假設選擇0-1損失函數：

$L(Y,f(X))=\left\{\begin{matrix} 1,Y \neq f(X)& \\ 0,Y=f(X)& \end{matrix}\right.$

其中 $f(X)$ 是分類決策函數。這時，期望風險函數為

$R_{exp}(f)=E[L(Y,f(X))]$

期望是對聯合分布 $P(X,Y)$ 取的。所以取條件期望

$R_{exp}(f)=E_{X}\sum_{k=1}^{K}[L(c_{k},f(X))]P(c_{k}|X)$

為了使期望風險最小化，只需對 $X=x$ 逐個最小化，因此有

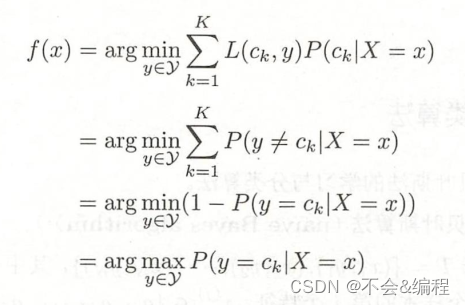
最終可知后驗概率最大的類=期望風險最小的類，即樸素貝葉斯采用的原理：

$f(x)=argmax_{c_{k}}P(c_{k}|X=x)$

2.2?樸素貝葉斯法的參數估計

2.2.1 極大似然估計

2.2.2 學習與分類算法

1 算法流程

2 例子

2.2.3 貝葉斯估計

1 理論

2 例子

取λ=1，之后如下所示：

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/11037.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/11037.shtml
英文地址，請注明出處：http://en.pswp.cn/web/11037.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！