機器學習作業4——樸素貝葉斯分類器

一、理論

一個例子：

二、代碼

對于代碼的解釋：

1.fit函數：

2.predict函數:

三、實驗結果

原因分析：

一、理論

樸素貝葉斯分類器基于貝葉斯定理進行分類，通過后驗概率來判斷將新數據歸為哪一類。通過利用貝葉斯定理計算后驗概率，并選擇具有最高后驗概率的類別作為預測結果，樸素貝葉斯分類器能夠在考慮了先驗概率和觀察到的數據特征后，做出基于統計推斷的分類決策，從而實現有效的分類。

步驟：

1.計算先驗概率：先驗概率表示了在沒有任何其他信息的情況下，一個數據點屬于每個類別的概率。

2.計算條件概率：條件概率表示了在給定某一類別的情況下，某個特征取某個值的概率。

3.計算后驗概率：當有一個新的數據點需要分類時，樸素貝葉斯根據該數據點的特征值，利用貝葉斯定理計算每個類別的后驗概率。后驗概率表示了在考慮了新的觀察結果后，每個類別的概率。

4.做出分類：根據計算得到的后驗概率，選擇具有最高后驗概率的類別作為預測結果。

先驗概率：

$P(Y=c_k) = \frac{|D_{c_k}|}{|D|}$

其中：ck是類別，D是數據數量，Dck是類別為ck的數據數量。

條件概率：

$P(X^{(i)}=a_{i,j}|Y=c_k) = \frac{|D_{c_k}^{(i)}(a_{i,j})|}{|D_{c_k}|}$

其中：Xi代表第i個特征，ai,j代表第i個特征中第j個類型， $D_{c_k}^{(i)}(a_{i,j})$ 代表在類別為ck時，在第i個特征中的第j個類型的數量。

后驗概率：

$P(Y=c_k|X=x) = \frac{P(Y=c_k) \cdot \prod_{j=1}^{n} P(X^{(j)}=x^{(j)}|Y=c_k)}{\sum_{i=1}^{K} P(Y=c_i) \cdot \prod_{j=1}^{n} P(X^{(j)}=x^{(j)}|Y=c_i)}$

因為我們只需要分類，因為不同后驗概率分母都相同，所以可以把分母去掉，只需要比較分子的大小即可，即：

$P(Y=c_k|X=x) = {P(Y=c_k) \cdot \prod_{i=1}^{n} P(X^{(i)}=x^{(i)}|Y=c_k)}$

其中： $\prod_{i=1}^{n} P(X^{(i)}=x^{(i)}|Y=c_k)$ 代表當前測試數據的每個類型為xi，在ck類別下的條件概率的連乘積。

可以看到公式簡潔了不少。

一個例子：

假設數據集：

特征1	特征2	類別
1	1	A
1	0	A
0	1	B
0	1	A
1	0	B

現在預測一個特征1為1，特證2為1的測試元組是什么類別。

首先計算類別的先驗概率和所有條件概率：

P(A)=?3/5，P(B)=?2/5

對于特征1：
P1(1∣A)=?2/3，P1(1 | B)= 1/2，

對于特征2：

P2(1?| A) = 2/3，P2(1?| B) = 1/2

然后計算預測為A和B的后驗概率，并比較大小，得出結果

P(A|X) = P(A)*P1(1∣A)*P2(1?| A) = 4/15
P(B|X) = P(B)*P1(1 | B)*P2(1 | B) = 1/10

可以看到P(A|X)比較大，所以是A類?

?

二、代碼

import numpy as np  
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score class NaiveBayesClassifier:def __init__(self):self.class_prior = {}  # 存儲類別的先驗概率self.feature_prob = {}  # 存儲特征在各個類別下的條件概率def fit(self, X, y):n_samples, n_features = X.shape  # 獲取樣本數和特征數self.classes = np.unique(y)  # 獲取目標標簽中的唯一類別值print("計算先驗概率:")for c in self.classes:# 統計每個類別在目標標簽中的出現次數，并除以樣本總數，得到先驗概率self.class_prior[c] = np.sum(y == c) / n_samplesprint("先驗概率: 類別， 概率 "+repr(c)+" "+repr(self.class_prior[c]))# 外層循壞遍歷類別，內層循環遍歷每個特征，內層循環每次要計算出每個特征下不同取值的在當前類別下的條件概率，存放到[c][feature_index]下print("計算條件概率：")for c in self.classes:self.feature_prob[c] = {}  # 初始化存儲特征條件概率的字典for feature_index in range(n_features):# 對于每個特征，統計在當前類別下的取值及其出現次數，并除以總次數，得到條件概率# values是feature_index列中不同的取值，counts是這些不同取值的個數（在類別為C下的）values, counts = np.unique(X[y == c, feature_index], return_counts=True)self.feature_prob[c][feature_index] = dict(zip(values, counts / np.sum(counts)))#dict是變為以values和counts/np.sum的字典，zip就是一個方便的操作for i in range(len(counts)):print("條件概率：P(" + repr(values[i]) + "|" + repr(c) + ") = " + repr(self.feature_prob[c][feature_index][values[i]]))def predict(self, X):predictions = []  # 存儲預測結果的列表#對于測試集中的每個元素cnt = 0for x in X:print("\n對于第" + repr(cnt) + "個測試集：")cnt+=1max_posterior_prob = -1  # 最大后驗概率初始化為-1predicted_class = None  # 預測類別初始化為空#對于每個類別for c in self.classes:# 計算后驗概率，先驗概率乘以各個特征的條件概率posterior_prob = self.class_prior[c]print("對于類別"+repr(c)+" = "+"[先驗"+repr(self.class_prior[c])+"]", end = '')#對于每個特征for feature_index, feature_value in enumerate(x):if feature_value in self.feature_prob[c][feature_index]:print(" * [P("+ repr(feature_value) + "|" + repr(c) + ") = " + repr(self.feature_prob[c][feature_index][feature_value]) + "]", end = '')posterior_prob *= self.feature_prob[c][feature_index][feature_value]else:print(" * 1")# 更新預測值print(" = " + repr(posterior_prob))if posterior_prob > max_posterior_prob:max_posterior_prob = posterior_probpredicted_class = cpredictions.append(predicted_class)  # 將預測結果添加到列表中return predictions  # 返回預測結果列表data = {'outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast', 'sunny', 'sunny', 'rain', 'rain', 'overcast', 'overcast', 'rain'],'temperature': ['hot', 'hot', 'hot', 'mild', 'cool', 'cool', 'cool', 'mild', 'cool', 'mild', 'mild', 'mild', 'hot', 'mid'],'humidity': ['high', 'high', 'high', 'high', 'normal', 'normal', 'normal', 'high', 'normal', 'normal', 'normal', 'high', 'normal', 'high'],'wind': ['weak', 'strong', 'weak', 'weak', 'weak', 'strong', 'strong', 'weak', 'weak', 'weak', 'strong', 'strong', 'weak', 'strong'],'playtennis': ['no', 'no', 'yes', 'yes', 'yes', 'no', 'yes', 'no', 'yes', 'yes', 'yes', 'yes', 'yes', 'no']
}
#創建DataFrame
df = pd.DataFrame(data)
X = df.drop('playtennis', axis=1)#axis=1刪除列，=0刪除行
y = df['playtennis']# 將數據集分為訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=3)
X_train = X_train.values#化為二維數組，便于遍歷
X_test = X_test.values
y_train = y_train.values
y_test = y_test.valuesprint("訓練集：")
for i in range(len(y_train)):print(repr(i)+": "+repr(X_train[i])+"  "+repr(y_train[i]))
print("測試集：")
for i in range(len(y_test)):print(repr(i)+": "+repr(X_test[i])+"  "+repr(y_test[i]))nb_classifier = NaiveBayesClassifier()
nb_classifier.fit(X_train, y_train)y_pred = nb_classifier.predict(X_test)
print("預測結果：")
for i in range(len(y_pred)):print(repr(i)+"正確,預測: "+repr(y_test[i])+", "+repr(y_pred[i]))accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred, pos_label='yes')
recall = recall_score(y_test, y_pred, pos_label='yes')
f1 = f1_score(y_test, y_pred, pos_label='yes')
print("準確率:", accuracy)  
print("精確率:", precision)  
print("召回率:", recall)  
print("f1:", f1)

對于重要代碼的解釋：

1.fit函數：

? ? ? 訓練測試集的主要代碼，先把訓練集中所有的條件概率和先驗概率算出來，在后面的預測中會使用到。

先驗概率：

print("計算先驗概率:")for c in self.classes:# 統計每個類別在目標標簽中的出現次數，并除以樣本總數，得到先驗概率self.class_prior[c] = np.sum(y == c) / n_samplesprint("先驗概率: 類別， 概率 "+repr(c)+" "+repr(self.class_prior[c]))

所有條件概率：

print("計算條件概率：")for c in self.classes:self.feature_prob[c] = {}  # 初始化存儲特征條件概率的字典for feature_index in range(n_features):# 對于每個特征，統計在當前類別下的取值及其出現次數，并除以總次數，得到條件概率# values是feature_index列中不同的取值，counts是這些不同取值的個數（在類別為C下的）values, counts = np.unique(X[y == c, feature_index], return_counts=True)self.feature_prob[c][feature_index] = dict(zip(values, counts / np.sum(counts)))for i in range(len(counts)):print("條件概率：P(" + repr(values[i]) + "|" + repr(c) + ") = " + repr(self.feature_prob[c][feature_index][values[i]]))

?結果：

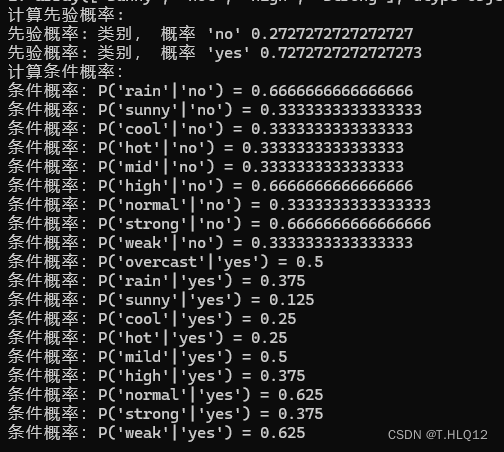
2.predict函數:

這個函數用于測試集的預測，對于測試集中的每個元組，都要對于所有類別，計算一次該類別下的后驗概率，然后選擇所有類別中后驗概率最大的，作為預測結果，而每個后驗概率，通過該元組下的每個特征下的類型對應的條件概率的累乘和該類別的先驗概率的乘積來確定。

對于每個元組：

for x in X:print("\n對于第" + repr(cnt) + "個測試集：")cnt+=1max_posterior_prob = -1  # 最大后驗概率初始化為-1predicted_class = None  # 預測類別初始化為空

對于每個類別：

for c in self.classes:posterior_prob = self.class_prior[c]

對于每個特征：

for feature_index, feature_value in enumerate(x):if feature_value in self.feature_prob[c][feature_index]:print(" * [P("+ repr(feature_value) + "|" + repr(c) + ") = " + repr(self.feature_prob[c][feature_index][feature_value]) + "]", end = '')posterior_prob *= self.feature_prob[c][feature_index][feature_value]else:print(" * 1")

每次計算完后，維護最大值以及類型：

if posterior_prob > max_posterior_prob:max_posterior_prob = posterior_probpredicted_class = c

每個元組計算完后，添加到預測數組中，最后返回預測數組即可。

三、實驗結果

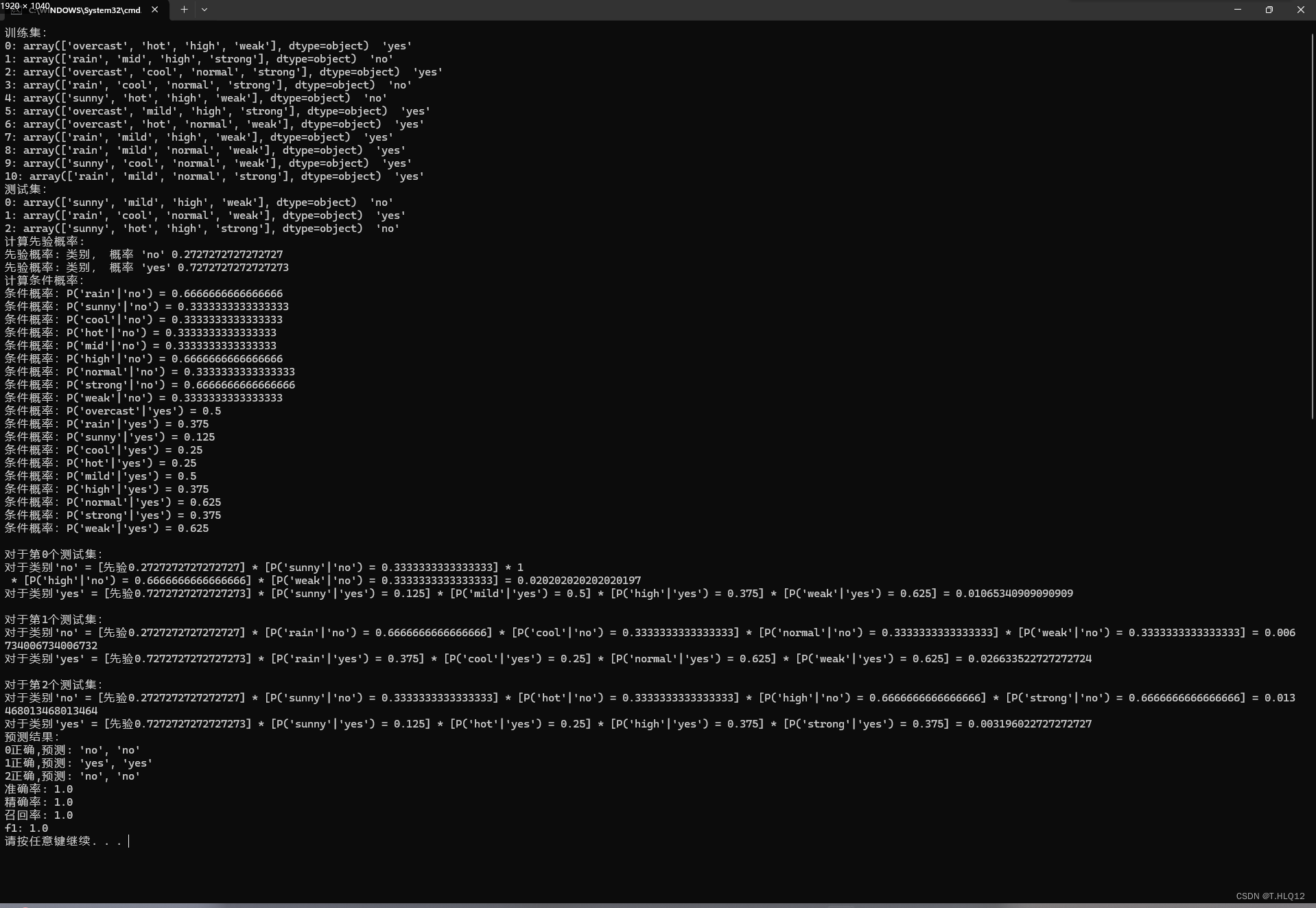
上圖是最好的一個實驗結果，所有指標為1，其他的實驗結果準確率較低

原因分析：

? ? ? ? 這個訓練集數據過小，但是特征和每個特征中的類型又比較多，再加上測試集一共就13條，數據使用不同的隨機種子會使得一些測試集中的特征在不同類別下的條件概率沒有出現過，因為沒有出現過，直接就不處理這個特征了，就容易出現誤差。

例如：

當隨機種子為1時：

當隨機種子為4時：

樸素貝葉斯分類器優缺點分析：

優點：

適用廣：樸素貝葉斯算法在處理大規模數據時表現良好，適用于許多實際問題。
對小規模數據表現良好：即使在小規模數據集上，樸素貝葉斯分類器也能有好的結果。
對缺失數據不敏感：樸素貝葉斯算法對缺失數據不敏感，即使有部分特征缺失或者未出現，仍然可以有效地進行分類。

缺點：

假設過于簡化：樸素貝葉斯假設特征之間相互獨立，在現實中，數據一般難以是真正獨立的，因此會導致結果不準確。
處理連續性特征較差：樸素貝葉斯算法通常假設特征是離散的，對于連續性特征的處理不夠靈活，可能會影響分類性能。