1. N叉樹的層序遍歷

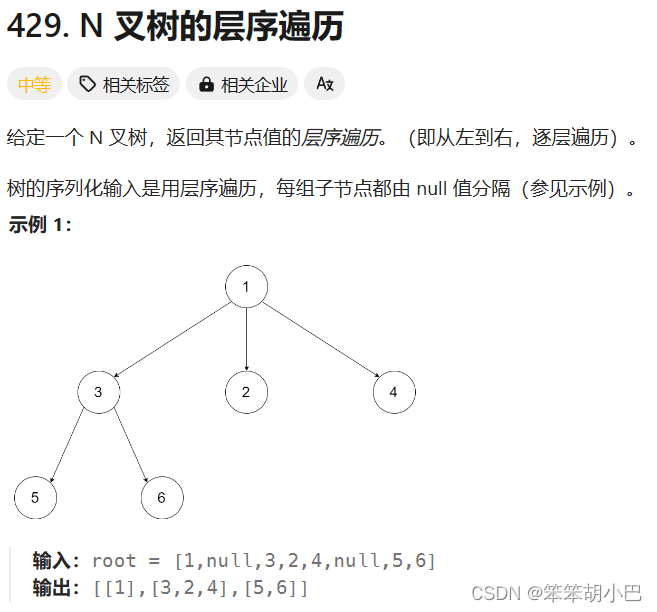
首先我們遇到這個題目，沒有任何思路，我們就可以來模擬一下層序的流程，首先我們肯定是訪問根節點1，訪問之后呢就是訪問下一層的最左節點3，此時第一層的節點1已經訪問過了就可以不要了，然后訪問第二層的中間節點2，最后訪問最右邊的節點4，然后就訪問第三層，此時第二層最做節點就不要了，此時我們會發現此時就滿足隊列的先進先出的特點，知道用什么數據結構了我們就直接上思路：

直接上代碼：

class Solution {
public:vector<vector<int>> levelOrder(Node* root) {vector<vector<int>> ret; //記錄最終結果queue<Node*> q;  // 層序遍歷需要的隊列if(root == nullptr)return ret;q.push(root); // 隊頭元素入隊while(!q.empty()){vector<int> tmp; //統計本層的節點int size = q.size(); //求出本層元素的個數while(size--){Node* n = q.front();q.pop();tmp.push_back(n->val);for(auto child : n->children) // 讓孩子入隊列{if(child != nullptr)q.push(child);}}ret.push_back(tmp);}return ret;}
};

2. 二叉樹的鋸齒形層序遍歷

這個題目上給我們說了層序遍歷，那么我們還是要用到隊列，我們會發現，這道題和我們上道題目是一樣的都是層序遍歷，唯一的區別就是偶數層的遍歷方式是我們之前的逆序，所以這道題目也很簡單，直接上思路：

直接來寫代碼：

class Solution {
public:vector<vector<int>> zigzagLevelOrder(TreeNode* root) {vector<vector<int>> ret;queue<TreeNode*> q;int flag = 1;//增加一個標記位,讓偶數行的信息逆序即可if(root == nullptr) return ret;q.push(root);while(!q.empty()){vector<int> tmp;int size = q.size(); while(size--){TreeNode* front = q.front();q.pop();tmp.push_back(front->val);if(front->left != nullptr)q.push(front->left);if(front->right != nullptr)q.push(front->right);}if(flag == 1)ret.push_back(tmp);else{reverse(tmp.begin(),tmp.end());ret.push_back(tmp);}  flag *= -1;}return ret;}
};

3. 在每個樹行中找最大值

我們這道題和之前的題目思路是一樣的，只不過這個題目我們不需要統計每層的節點，只需要統計最大的哪一個節點即可，所以在層序遍歷過程中，在執?讓下?層節點?隊的時候，我們可以在循環中統計出當前層結點的最大值的，直接上思路：

直接來寫代碼：

class Solution {
public:vector<int> largestValues(TreeNode* root) {vector<int> ret;if(root == nullptr) return ret;queue<TreeNode*> q;q.push(root);while(q.size()) // 如果隊列不為空{int maxnum = INT_MIN;int size = q.size();while(size--){TreeNode* t = q.front();q.pop();maxnum = max(maxnum, t->val); // 記錄每層的最大值if(t->left) q.push(t->left);if(t->right) q.push(t->right);}ret.push_back(maxnum);}return ret;}
};

4.二叉樹的最大寬度

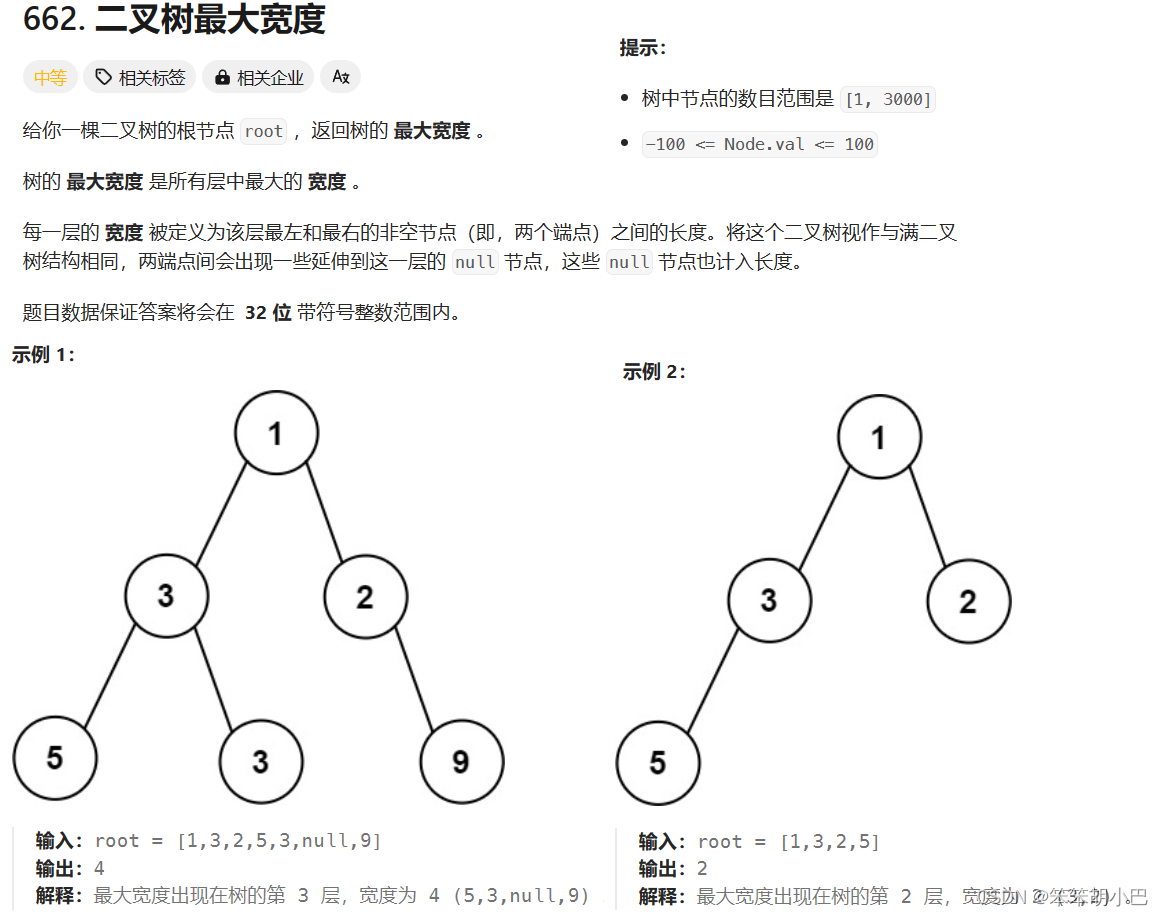
題目解析：

這道題相較于上面三道題就有點難度了，這個題目男難就難在處理空節點，既然統計每一層的最大寬度，我們優先想到的就是利用層序遍歷，把當前層的結點全部存在隊列?面，利用隊列的常度來計算每一層的寬度，統計出最大的寬度。但是，由于空節點也是需要計算在內的。因此，我們可以選擇將空節點也存在隊列??。

?解法一：

這個思路是我們正常會想到的思路，但是極端境況下，最左邊?條長鏈，最右邊?條長鏈，我們需要存幾億個空節點，會超過最?內存限制。

?解法二：利用數組存儲二叉樹的方式，給節點編號

依舊是利?層序遍歷，但是這?次隊列??不單單存結點信息，并且還存儲當前結點如果在數組中存儲所對應的下標（在我們學習數據結構堆的時候，計算左右孩子的方式）。

這樣我們計算每?層寬度的時候，?需考慮空節點，只需將當層結點的左右結點的下標相減再加 1即可，我們直接上思路：?

魔鬼細節：

極端境況下，最左邊?條長鏈，最右邊?條長鏈，我們需要存幾億個空節點，會超過最?內存限制，那么此時我們的編號是2的1500次方，那么肯定會越界，此時無論什么數據類型我們都存不下，但是這個題最后我們是會進行減法的，但是我們數據的存儲是?個環形的結構，并且題?說明，數據的范圍在 int 這個類型的最大值的范圍之內，因此不會超出?圈； 因此，如果是求差值的話，我們?需考慮溢出的情況，由于c++溢出使用int會報錯，因此我們使用unsigned int來存儲這個數據。直接上代碼：

class Solution {
public:int widthOfBinaryTree(TreeNode* root) {queue<pair<TreeNode*, unsigned int>> q;q.push({root,1}); // 根節點和編號入隊unsigned int ret = 0; // 最大寬度while(q.size()){// 先更新這?層的寬度auto& [x1, y1] = q.front();auto& [x2, y2] = q.back();ret = max(ret, y2 - y1 + 1);int size = q.size();// 讓下?層進隊while(size--){auto [a,b] = q.front(); q.pop();if(a->left) q.push({a->left, 2*b});if(a->right) q.push({a->right,2*b+1});}}return ret;}
};

其實這道題我們也可以用數組來實現，但是這時候有人說了此時我們會經常進行刪除節點，而刪除節點都是頭刪，而數組的頭刪效率較低，你咋還使用我們的數組呢？確實是這樣，但是我們進行刪除節點不一定要頭刪，我們可以把本層的節點用tmp統計出來，然后拷貝給q即可。

class Solution {
public:int widthOfBinaryTree(TreeNode* root) {vector<pair<TreeNode*,unsigned int>> q; // 用數組模擬隊列 q.push_back(make_pair(root,1));unsigned int ret = 0;while(!q.empty()){// 先更新這?層的寬度auto& [x1, y1] = q[0];auto& [x2, y2] = q.back();ret = max(ret, y2 - y1 + 1);// 讓下?層進隊vector<pair<TreeNode*, unsigned int>> tmp; // 讓下?層進?這個隊列for(auto [x, y] : q){if(x->left) tmp.push_back({x->left, y * 2});if(x->right) tmp.push_back({x->right, y * 2 + 1});}q = tmp; // 避免了頭刪效率低的問題}return ret;}
};