前言

在這篇文章中，我們一起來看看我們生活中都會用到，但卻不那么熟悉的數據結構——圖（英語：graph）。我們看下百科定義：

在計算機科學中，圖（英語：graph）是一種抽象數據類型，用于實現數學中圖論的無向圖和有向圖的概念。

圖的數據結構包含一個有限（可能是可變的）的集合作為節點集合，以及一個無序對（對應無向圖）或有序對（對應有向圖）的集合作為邊（有向圖中也稱作弧）的集合。節點可以是圖結構的一部分，也可以是用整數下標或引用表示的外部實體。

圖的數據結構還可能包含和每條邊相關聯的數值（edge value），例如一個標號或一個數值（即權重，weight；表示花費、容量、長度等）。

從上面定義，我們知道圖分為有向圖和無向圖，圖是由頂點和邊，還有可能權重。我們看看圖在哪些方面有應用：交通運輸規劃，每個地方就是圖的頂點，而每條路就是圖的邊；社交網絡分析，每個用戶就是頂點，而用戶之間是否為好友就是邊；互聯網，每個網頁就是頂點，而網頁上跳轉到其他網頁就是邊，我們每天使用的百度，谷歌搜索引擎實現其中用到很重要技術就是圖。還有像電路設計，通信網絡，計劃與排程問題都用到了圖數據結構來表示他們的關系。

起源（歐拉與柯尼斯堡的七橋問題）

十八世紀，在今天俄羅斯加里寧格勒市還被稱為柯尼斯堡的年代。像其他許多大城市一樣，一條大河(普列戈利亞河)穿城而過。柯尼斯堡除了被一分為二以外，還包含河中的兩個島嶼，人們建有七座橋梁連接著不同的陸地。當時有一個著名的游戲謎題，就是在所有橋都只能走一遍的前提下，怎樣才能把這片區域所有的橋都走遍?這個謎題成為當地人一項熱衷的消遭運動，許多人聲稱已經找到了這樣一條路徑，但當被要求按照規則再走一遍時，卻發現還是沒有人能夠做到。直到 1736 年，瑞士數學家萊昂哈德·歐拉給出了答案，他在論文《柯尼斯堡的七橋》中解釋了其中的原因，證明這樣的步行方式并不存在，并在文中提出和解決了一筆畫問題。

萊昂哈德·歐拉（Leonhard Euler，1707年4月15日–1783年9月18日）是18世紀最杰出的數學家之一，同時也是物理學、天文學和工程學領域的重要貢獻者。大家感興趣可以看下號稱數學最美公式之一的歐拉公式。

圖論基礎知識

圖由節點（Vertex）和連接節點的邊（Edge）組成。

節點（Vertex）：圖中的基本元素，也稱為頂點。節點可以代表各種事物，如城市、人物、物體等。邊（Edge）：連接圖中兩個節點的線，表示節點之間的關系。邊可以是有向的（箭頭指向特定的方向）或無向的（沒有箭頭，表示雙向關系）。度（Degree）：節點的度是與其相連的邊的數量。對于有向圖，節點的度分為入度（In-Degree）和出度（Out-Degree），分別表示指向該節點的邊的數量和從該節點出發的邊的數量。路徑（Path）：圖中連接節點的一系列邊構成的序列。路徑的長度是指路徑上的邊的數量。如果路徑中的所有節點都是不同的，則稱該路徑是簡單路徑。環（Cycle）：由圖中一系列邊構成的閉合路徑，起點和終點相同，并且路徑中的節點都是不同的。連通性（Connectivity）：一個圖被稱為連通的，如果從圖中的任意一個節點到另一個節點都存在至少一條路徑。如果一個圖不是連通的，則可以分為多個連通分量。圖的類型：根據圖中邊的性質，圖可以分為有向圖（Directed Graph）和無向圖（Undirected Graph）。此外，圖還可以是加權的，即邊上帶有權重（Weight）。鄰接矩陣（Adjacency Matrix）和鄰接表（Adjacency List）：這兩種數據結構用于表示圖的連接關系。鄰接矩陣是一個二維數組，其中的元素表示節點之間是否相連。鄰接表是由一組鏈表或數組構成的數據結構，用于表示每個節點的鄰居節點。

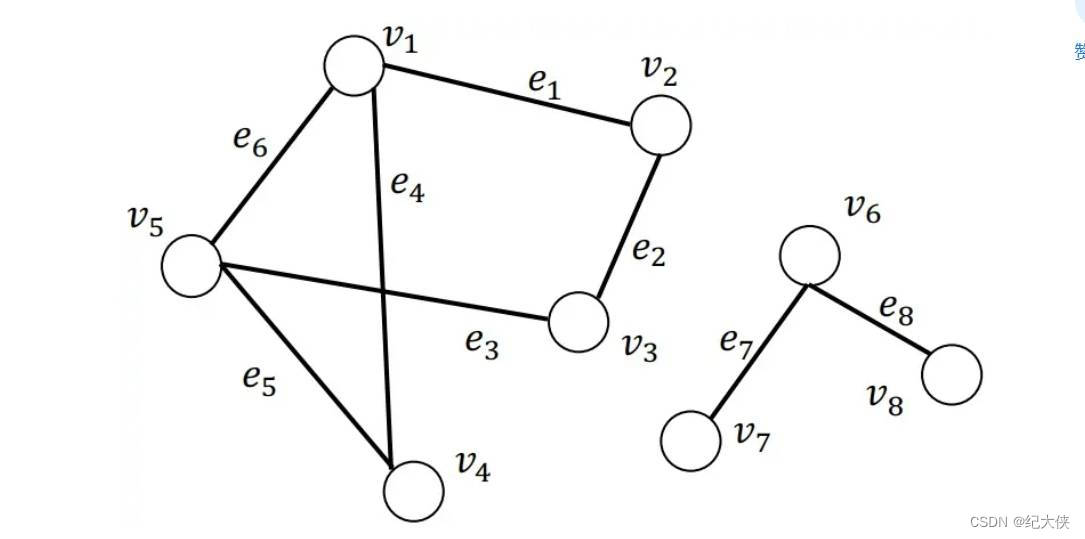
上圖我們發現，右邊就是我們熟悉的圖。那么圖在什么情況下能叫做樹。
樹是一種特殊的無向圖。

無向圖：樹是一種無向圖，其中任意兩個節點之間都有唯一的簡單路徑。
連通圖：樹是連通圖，即從任意一個節點出發，都可以到達圖中的所有其他節點。換句話說，樹是一個連通且無環的圖。
無回路：樹不包含回路，即沒有形成環的路徑。每個節點都只能通過一條路徑到達另一個節點，因此樹不會出現閉合的環路。
N個節點的樹有N-1條邊：如果一個無向圖含有N個節點，并且是樹的話，那么它必然有N-1條邊。這個特性被稱為樹的性質之一。

圖表示方式

**鄰接矩陣（Adjacency Matrix）和鄰接表（Adjacency List）**是兩種常用的圖表示方法，它們各自有自己的優缺點：

鄰接矩陣的優缺點：

優點：
直觀易懂：鄰接矩陣直觀地展示了圖中節點之間的連接關系，易于理解和實現。
快速查找：可以在O(1)的時間內查找兩個節點之間是否有邊相連。
適用于稠密圖：對于邊的數量較多的稠密圖，鄰接矩陣的空間復雜度較低，使用更為高效。
缺點：

空間復雜度高：鄰接矩陣需要使用N^2的空間來存儲N個節點的連接關系，對于稀疏圖來說，會浪費大量空間。
不適用于大規模圖：當圖規模很大時，鄰接矩陣的空間開銷會變得非常巨大，導致內存不足或效率低下。
無法存儲邊的權重：如果圖中的邊有權重，鄰接矩陣需要額外的空間來存儲這些權重信息，增加了復雜度。

下面是用Java實現鄰接矩陣表示圖

import java.util.Arrays;public class AdjacencyMatrix {private int[][] matrix;private int numVertices;public AdjacencyMatrix(int numVertices) {this.numVertices = numVertices;matrix = new int[numVertices][numVertices];}// 添加邊public void addEdge(int src, int dest) {matrix[src][dest] = 1;matrix[dest][src] = 1; // 無向圖，所以需要反向也設置為1}// 刪除邊public void removeEdge(int src, int dest) {matrix[src][dest] = 0;matrix[dest][src] = 0; // 無向圖，所以需要反向也設置為0}// 打印鄰接矩陣public void printMatrix() {for (int i = 0; i < numVertices; i++) {System.out.println(Arrays.toString(matrix[i]));}}public static void main(String[] args) {int numVertices = 5;AdjacencyMatrix graph = new AdjacencyMatrix(numVertices);// 添加邊graph.addEdge(0, 1);graph.addEdge(0, 4);graph.addEdge(1, 2);graph.addEdge(1, 3);graph.addEdge(1, 4);graph.addEdge(2, 3);graph.addEdge(3, 4);// 打印鄰接矩陣graph.printMatrix();}
}

鄰接表的優缺點：

優點：

空間利用率高：鄰接表只存儲有連接關系的節點，對于稀疏圖來說，空間利用率更高。
易于插入和刪除邊：在鄰接表中，插入或刪除邊的操作更為高效，時間復雜度為O(1)。
適用于稀疏圖：對于邊的數量較少的稀疏圖，鄰接表的空間復雜度更低，更加節省內存空間。
缺點：

查找邊的時間復雜度高：在鄰接表中查找兩個節點之間是否有邊相連，時間復雜度為O(n)，其中n為節點的度數。
不適用于密集圖：對于邊的數量較多的密集圖，鄰接表的空間復雜度會增加，效率較低。
不適合快速查找：如果需要頻繁進行兩個節點之間是否相連的查找操作，鄰接表的效率可能不如鄰接矩陣。

下面是用Java實現表示鄰接表

import java.util.*;public class AdjacencyList {private Map<Integer, List<Integer>> adjList;public AdjacencyList() {adjList = new HashMap<>();}// 添加節點public void addNode(int node) {adjList.put(node, new LinkedList<>());}// 添加邊public void addEdge(int src, int dest) {adjList.get(src).add(dest);adjList.get(dest).add(src); // 無向圖，所以需要反向也添加}// 刪除邊public void removeEdge(int src, int dest) {adjList.get(src).remove((Integer) dest);adjList.get(dest).remove((Integer) src); // 無向圖，所以需要反向也刪除}// 打印鄰接表public void printList() {for (Map.Entry<Integer, List<Integer>> entry : adjList.entrySet()) {System.out.print(entry.getKey() + " -> ");for (Integer neighbor : entry.getValue()) {System.out.print(neighbor + " ");}System.out.println();}}public static void main(String[] args) {AdjacencyList graph = new AdjacencyList();// 添加節點for (int i = 0; i < 5; i++) {graph.addNode(i);}// 添加邊graph.addEdge(0, 1);graph.addEdge(0, 4);graph.addEdge(1, 2);graph.addEdge(1, 3);graph.addEdge(1, 4);graph.addEdge(2, 3);graph.addEdge(3, 4);// 打印鄰接表graph.printList();}
}

最短路徑算法

圖的最短路徑算法用于找到兩個節點之間的最短路徑。

迪杰斯特拉算法（Dijkstra Algorithm）

package demo.algorithm.algorithm;import java.util.*;
/***最短路徑算法-迪杰斯特拉(Dijkstra)算法（1956年發表）* 迪杰斯特拉(Dijkstra)算法是典型最短路徑算法，用于計算一個節點到其他節點的最短路徑。* Dijkstra 算法是一個基于「貪心」、「廣度優先搜索」、「動態規劃」求一個圖中一個點到其他所有點的最短路徑的算法，時間復雜度 O(n2)* 每次從 「未求出最短路徑的點」中 取出 距離距離起點 最小路徑的點，以這個點為橋梁 刷新「未求出最短路徑的點」的距離* 迪杰斯特拉(Dijkstra)算法，能處理有環圖，不能處理含有負權邊的圖.** 如果存在負權重，則可能在之后的計算中得到總權重更小的路徑，從而影響之前的結果（譯注：即可能出現多繞路反而路線更短的情況，不合實際）。* @author jishenglong on 2023/1/24 9:14**/
public class DijkstraAlgorithm {private static final int INF = Integer.MAX_VALUE; // 無窮大表示不可達public static void dijkstra(int[][] graph, int start, int end) {int n = graph.length; // 圖的頂點數int[] dist = new int[n]; // 存儲起始點到各個頂點的最短距離boolean[] visited = new boolean[n]; // 標記頂點是否已訪問int[] prev = new int[n]; // 記錄最短路徑中的前驅頂點// 初始化距離數組和前驅數組Arrays.fill(dist, INF);Arrays.fill(prev, -1);dist[start] = 0;// 開始算法for (int i = 0; i < n - 1; i++) {int minDist = INF;int minIndex = -1;// 找到當前未訪問頂點中距離起始點最近的頂點for (int j = 0; j < n; j++) {if (!visited[j] && dist[j] < minDist) {minDist = dist[j];minIndex = j;}}System.out.println(String.format("minIndex:%s,minDist:%s",minIndex,minDist ));// 標記該頂點為已訪問visited[minIndex] = true;// 更新與該頂點相鄰頂點的最短距離和前驅頂點for (int j = 0; j < n; j++) {if (!visited[j] && graph[minIndex][j] != INF) {int newDist = dist[minIndex] + graph[minIndex][j];if (newDist < dist[j]) {dist[j] = newDist;prev[j] = minIndex;}}}}System.out.println("cost: " + dist[end]);// 打印最短路徑printShortestPath(prev, start, end);}// 遞歸打印最短路徑private static void printShortestPath(int[] prev, int start, int end) {if (end == start) {System.out.print(start);} else if (prev[end] == -1) {System.out.println("No path exists from " + start + " to " + end);} else {printShortestPath(prev, start, prev[end]);System.out.print(" -> " + end);}}public static void main(String[] args) {int[][] graph = {{0, 4, 2, INF, INF},{4, 0, 1, 5, INF},{2, 1, 0, 8, 10},{INF, 5, 8, 0, 2},{INF, INF, 10, 2, 0}};int start = 0; // 起始點int end = 3; // 終點dijkstra(graph, start, end);}
}

Floyd算法

package demo.algorithm.algorithm;/*** 最短路徑算法* Floyd算法是一個經典的動態規劃算法，它又被稱為插點法。該算法名稱以創始人之一、1978年圖靈獎獲得者、斯坦福大學計算機科學系教授羅伯特·弗洛伊德命名。* Floyd算法是一種利用動態規劃的思想尋找給定的加權圖中多源點之間最短路徑的算法,算法目標是尋找從點i到點j的最短路徑。* 時間復雜度:O(n^3)；空間復雜度:O(n^2)* 弗洛伊德算法是解決任意兩點間的最短路徑的一種算法，可以正確處理有向圖或有向圖或負權（但不可存在負權回路)的最短路徑問題，同時也被用于計算有向圖的傳遞閉包** @author jishenglong on 2023/1/24 9:51**/
public class FloydAlgorithm {private int numVertices;private int[][] distance;public FloydAlgorithm(int numVertices) {this.numVertices = numVertices;this.distance = new int[numVertices][numVertices];// 初始化距離矩陣，表示頂點之間的初始距離for (int i = 0; i < numVertices; i++) {for (int j = 0; j < numVertices; j++) {if (i == j) {distance[i][j] = 0; // 頂點到自身的距離為0} else {distance[i][j] = Integer.MAX_VALUE; // 初始化為無窮大}}}}// 添加邊和權重public void addEdge(int source, int destination, int weight) {distance[source][destination] = weight;// 如果是有向圖，注釋掉下一行distance[destination][source] = weight;}/*** 佛洛伊德算法的核心方法* 在三重循環的每一次迭代中，我們檢查通過中間頂點 k 是否能夠獲得更短的路徑。* 具體操作是檢查從頂點 i 到頂點 k 的路徑與從頂點 k 到頂點 j 的路徑之和是否小于從頂點 i 到頂點 j 的當前已知路徑。如果是，則更新最短路徑* <p>* 外層循環 (k): 該循環遍歷所有可能的中間頂點。在每次迭代中，k 表示中間頂點，我們嘗試看看通過中間頂點是否能夠找到更短的路徑。* 第一層內層循環 (i): 該循環遍歷所有可能的起始頂點。* 第二層內層循環 (j): 該循環遍歷所有可能的目標頂點*/public void floydWarshall() {// 三重循環，依次考慮每個頂點作為中間點的情況for (int k = 0; k < numVertices; k++) {for (int i = 0; i < numVertices; i++) {for (int j = 0; j < numVertices; j++) {if (distance[i][k] != Integer.MAX_VALUE && distance[k][j] != Integer.MAX_VALUE &&distance[i][k] + distance[k][j] < distance[i][j]) {distance[i][j] = distance[i][k] + distance[k][j];}}}}// 打印最短路徑矩陣printShortestPaths();}private void printShortestPaths() {System.out.println("Shortest paths between all pairs of vertices:");for (int i = 0; i < numVertices; i++) {for (int j = 0; j < numVertices; j++) {if (distance[i][j] == Integer.MAX_VALUE) {System.out.print("INF\t");} else {System.out.print(distance[i][j] + "\t");}}System.out.println();}}public static void main(String[] args) {int numVertices = 4;FloydAlgorithm floydGraph = new FloydAlgorithm(numVertices);floydGraph.addEdge(0, 1, 3);floydGraph.addEdge(0, 2, 5);floydGraph.addEdge(1, 2, 1);floydGraph.addEdge(2, 3, 7);floydGraph.floydWarshall();}
}

當我們只要求一個節點到其他節點的最短路徑那么迪杰斯特拉(Dijkstra)算法比較適合；如果要求任意兩點間的最短路徑那么Floyd算法比較適合。

K短路

有時候需求是需要展示從A點到B點，3條最短路徑，也就是k短路。k短路問題，可以參考以下文章k 短路

package demo.algorithm.algorithm;import java.util.ArrayList;
import java.util.List;
import java.util.PriorityQueue;/*** AStar K短路* https://oi-wiki.org/graph/kth-path/** @author jisl on 2023/12/20 15:54**/
public class AStarKPaths {// 定義常量：表示無窮大的邊權值final int inf = Integer.MAX_VALUE / 2;// 聲明變量：節點數量int n;// 聲明數組：存儲節點的啟發式值int[] H;// 聲明數組：記錄節點在搜索過程中被訪問的次數int[] cnt;// 聲明變量：記錄當前處理的正向邊和逆向邊的數量int cur, cur1;// 正向圖的鄰接表int[] h;  // 頭結點int[] nxt;  // 下一條邊的索引int[] p;    // 相鄰節點的編號int[] w;    // 邊的權重// 逆向圖的鄰接表int[] h1;  // 頭結點int[] nxt1;  // 下一條邊的索引int[] p1;    // 相鄰節點的編號int[] w1;    // 邊的權重// 聲明數組：記錄節點是否被訪問過boolean[] tf;// 構造函數public AStarKPaths(int vertexCnt, int edgeCnt) {n = vertexCnt;//數組從0開始，要定義訪問到vertexCnt，那么數組長度需要+1int vertexLen = vertexCnt + 1;int edgeLen = edgeCnt + 1;// 初始化數組H = new int[vertexLen];cnt = new int[vertexLen];h = new int[vertexLen];nxt = new int[edgeLen];p = new int[edgeLen];w = new int[edgeLen];h1 = new int[vertexLen];nxt1 = new int[edgeLen];p1 = new int[edgeLen];w1 = new int[edgeLen];tf = new boolean[vertexLen];}/*** 添加正向圖的邊** @param x 起點* @param y 終點* @param z 邊的權重*/void addEdge(int x, int y, int z) {// 當前邊的索引cur++;// 將當前邊的下一條邊指向原來的頭結點nxt[cur] = h[x];// 更新頭結點為當前邊的索引h[x] = cur;// 記錄相鄰節點和邊的權重p[cur] = y;w[cur] = z;}/*** 添加逆向圖的邊** @param x 起點* @param y 終點* @param z 邊的權重*/void addEdge1(int x, int y, int z) {// 當前逆向邊的索引cur1++;// 將當前逆向邊的下一條邊指向原來的逆向頭結點nxt1[cur1] = h1[x];// 更新逆向頭結點為當前逆向邊的索引h1[x] = cur1;// 記錄逆向相鄰節點和邊的權重p1[cur1] = y;w1[cur1] = z;}/*** 節點類，用于A*算法中表示搜索過程中的節點*/class Node implements Comparable<Node> {int x, v; // 節點編號和從起點到該節點的累計代價List<Integer> path; // 存儲路徑/*** 構造方法，初始化節點** @param x    節點編號* @param v    從起點到該節點的累計代價* @param path 從起點到該節點的路徑*/Node(int x, int v, List<Integer> path) {this.x = x;this.v = v;this.path = new ArrayList<>(path);this.path.add(x); // 將當前節點加入路徑}/*** 優先隊列比較方法，根據節點的估值（v + H[x]）升序排序** @param a 另一個節點* @return 比較結果，1表示大于，-1表示小于*/@Overridepublic int compareTo(Node a) {return v + H[x] > a.v + H[a.x] ? 1 : -1;}}PriorityQueue<Node> q = new PriorityQueue<>();/*** 節點類，用于Dijkstra算法中表示搜索過程中的節點*/class Node2 implements Comparable<Node2> {int x, v; // 節點編號和從起點到該節點的累計代價/*** 構造方法，初始化節點** @param x 節點編號* @param v 從起點到該節點的累計代價*/Node2(int x, int v) {this.x = x;this.v = v;}/*** 優先隊列比較方法，根據節點的累計代價（v）升序排序** @param a 另一個節點* @return 比較結果，1表示大于，-1表示小于*/@Overridepublic int compareTo(Node2 a) {return v > a.v ? 1 : -1;}}PriorityQueue<Node2> Q = new PriorityQueue<>();/*** 構建圖并執行 A* K 短路算法** @param graph 圖的鄰接矩陣，表示節點間的邊權值* @param s     起點(source)* @param t     目標節點(target)* @param k     要求的最短路徑數量*/public void build(int[][] graph, int s, int t, int k) {// 起點s、目標節點t、路徑數量k等// 讀取圖的邊信息并構建正向圖和逆向圖for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (graph[i][j] != Integer.MAX_VALUE / 2) {addEdge(i, j, graph[i][j]);addEdge1(j, i, graph[i][j]);}}}// 初始化啟發式數組H，使用逆向邊進行估值for (int i = 1; i <= n; i++) {H[i] = inf;}// 使用 Dijkstra 算法計算從目標節點 t 到其他節點的估值 HQ.add(new Node2(t, 0));while (!Q.isEmpty()) {Node2 x = Q.poll();if (tf[x.x]) {continue;}tf[x.x] = true;
//            啟發式數組H 在Node節點比較的時候使用H[x.x] = x.v;for (int j = h1[x.x]; j != 0; j = nxt1[j]) {Q.add(new Node2(p1[j], x.v + w1[j]));}}// 使用 A* 算法計算從起點 s 到目標節點 t 的 k 條最短路徑q.add(new Node(s, 0, new ArrayList<>())); // 將起點 s 加入優先隊列 q，初始累計代價為 0，路徑為空列表while (!q.isEmpty()) {Node x = q.poll(); // 彈出當前累計代價最小的節點cnt[x.x]++; // 增加當前節點的訪問次數if (x.x == t) {// 如果當前節點是目標節點，輸出 A* K 短路算法的相關信息，包括路徑System.out.println(String.format("AStarKPaths對應值:x.v=%s,cnt[x.x]=%s,path=%s", x.v, cnt[x.x], getPath(x.path, s, t)));}if (x.x == t && cnt[x.x] == k) {System.out.println(x.v); // 如果找到第 k 條最短路徑，輸出累計代價并結束return;}if (cnt[x.x] > k) {continue; // 如果當前節點訪問次數超過 k，跳過后續處理}for (int j = h[x.x]; j != 0; j = nxt[j]) {q.add(new Node(p[j], x.v + w[j], new ArrayList<>(x.path))); // 將該節點的鄰接節點加入優先隊列，并更新累計代價和路徑}}System.out.println("-1");}private String getPath(List<Integer> path, int a, int b) {StringBuilder result = new StringBuilder();result.append("Shortest distance from ").append(a).append(" to ").append(b).append(": ");for (int i = 0; i < path.size(); i++) {result.append(" -> ").append(path.get(i));}result.append("\n==================================");return result.toString();}public static void main(String[] args) {int INF = Integer.MAX_VALUE / 2;int[][] graph = {{INF, 4, 2, INF, INF},{4, INF, 6, 5, INF},{2, 1, INF, 8, 10},{INF, 5, 8, INF, 2},{INF, INF, 10, 2, INF}};final AStarKPaths aStarKPaths = new AStarKPaths(graph.length, graph.length * graph.length);aStarKPaths.build(graph, 0, 3, 3);}
}

總結

以上簡單介紹了，圖論知識。對于圖論中用的比較多最短路和k短路用Java實現了。實際圖論是比較難的問題，這邊只是做了簡單的介紹，拋磚引玉。