1. 定義與作用
什么是激活函數?激活函數有什么用?
答:激活函數(Activation Function)是一種添加到人工神經網絡中的函數,
旨在幫助網絡學習數據中的復雜模式。類似于人類大腦中基于神經元的模型,激活函數最終決定了要發射給下一個神經元的內容。
核心作用:
- 引入非線性能力
在人工神經網絡中,其主要作用是對所有的隱藏層和輸出層添加一個非線性的操作,使得神經網絡的輸出更為復雜、表達能力更強。若神經網絡中不使用激活函數,無論網絡有多少層,其整體仍等價于一個線性模型。激活函數通過引入非線性變換,使網絡能夠學習和逼近復雜的非線性關系,從而具備強大的表達能力(representation power),這是深度學習能夠處理圖像、語音、自然語言等復雜任務的基礎。
- 控制神經元的激活狀態
激活函數對加權輸入進行變換,決定當前神經元的輸出強度或是否“激活”。例如,ReLU 在輸入為負時輸出為0,實現了稀疏激活,有助于提升模型效率和泛化能力。
- 影響梯度傳播與訓練穩定性
絕大多數神經網絡采用基于梯度下降的優化方法(如SGD、Adam),因此激活函數通常需要是可微分(或幾乎處處可微)的,以便通過反向傳播算法計算梯度。然而,某些激活函數(如
Sigmoid 或 Tanh)在輸入值過大或過小時會出現梯度飽和現象,導致梯度消失(vanishing gradient),嚴重影響深層網絡的訓練效率。
- 促進特征選擇與模型表達多樣性
不同的激活函數具有不同的數學特性(如輸出范圍、稀疏性、零中心性、是否可導等),合理選擇可提升模型性能。例如:
- Sigmoid:輸出范圍為 (0,1),適合二分類任務的輸出層,用于表示概率;
- Softmax:常用于多分類任務的輸出層,將輸出轉化為類別概率分布;
- ReLU 及其變體(如 Leaky ReLU、ELU、GELU):廣泛用于隱藏層,具備良好梯度傳播特性,緩解梯度消失問題;
- 線性激活函數(Identity):輸出等于輸入,常用于回歸任務的輸出層,不限制輸出范圍。
激活函數分類:
激活函數能分成兩類——飽和激活函數和非飽和激活函數。

- 右飽和:
當x趨向于正無窮時,函數的導數趨近于0,此時稱為右飽和
- 左飽和:
當x趨向于負無窮時,函數的導數趨近于0,此時稱為左飽和
- 飽和函數和非飽和函數:
一個函數既滿足右飽和,又滿足左飽和,則稱為飽和函數否則稱為非飽和函數。
2. 常用激活函數解析
2.1 Sigmoid函數
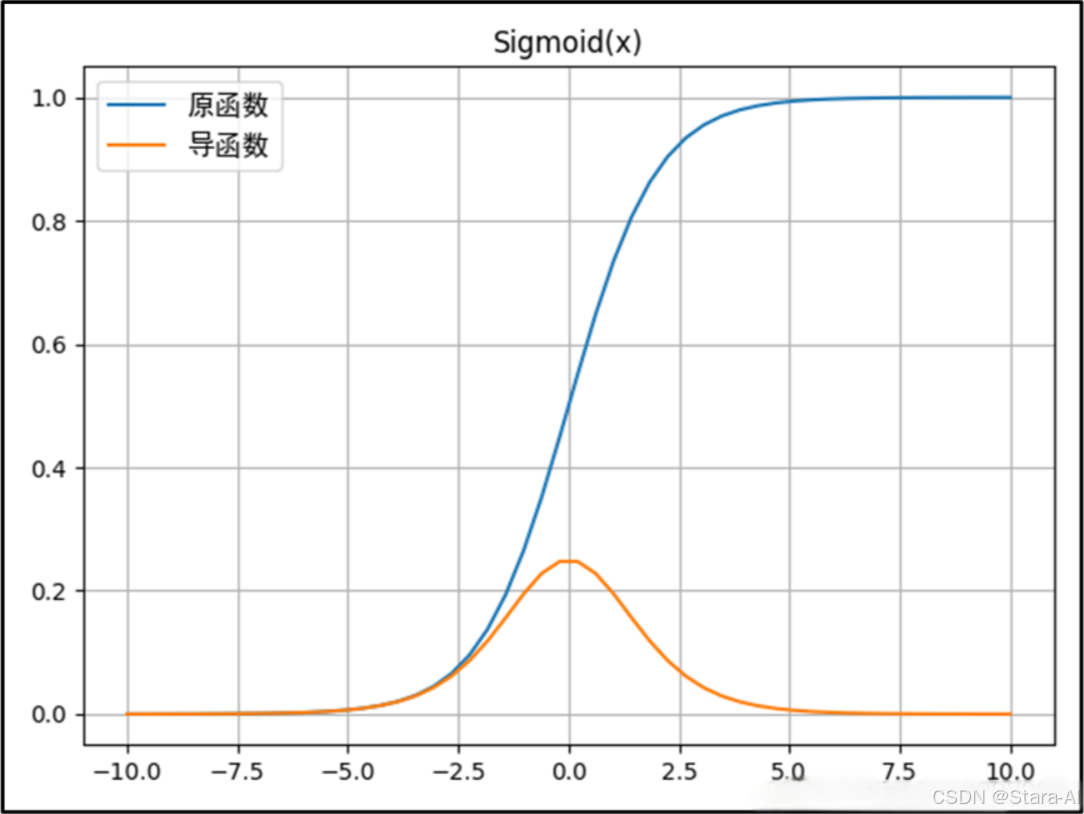
Sigmoid函數的定義:f(x)=11+e?xf(x) = \frac{1}{1 + e^{-x}}f(x)=1+e?x1?Sigmoid函數的導數:f′(x)=e?x(1+e?x)2=f(x)(1?f(x))f'(x) = \frac{e^{-x}}{(1 + e^{-x})^2} = f(x)(1 - f(x))f′(x)=(1+e?x)2e?x?=f(x)(1?f(x))
優點:
- 其值域為
[0,1],非常適合作為模型的輸出函數用于輸出一個(0,1)范圍內的概率值,可用于將預測概率作為輸出的模型,比如用于表示二分類的類別或者用于表示置信度。 Sigmoid函數的輸出范圍是0到1。由于輸出值限定在0到1,因此它對每個神經元的輸出進行了歸一化。- 該函數是連續可導的(即可微),可以提供非常平滑的梯度值,防止模型訓練過程中出現突變的梯度(即避免跳躍的輸出值)。
不足:
- 從其導數的函數圖像上可以看到,其導數的最大值只有0.25,而且當x在
[-5,5]的范圍外時其導數值就已經幾乎接近于0了。這種情況會導致訓練過程中神經元處于一種飽和狀態,反向傳播時其權重幾乎得不到更新,從而使得模型變得難以訓練,這種現象被稱為梯度消失問題。 - 其輸出不是以0為中心而是都大于0的(這會降低權重更新的效率),這樣下一層的神經元會得到上一層輸出的全正信號作為輸入,所以
Sigmoid激活函數不適合放在神經網絡的前面層而一般是放在最后的輸出層中使用。 - 需要進行指數運算(計算機運行得較慢),計算量大及計算復雜度高,訓練耗時;指數的越大其倒數就越小,容易產生梯度消失。
Pytorch代碼:
import torch
import torch.nn as nn# Sigmoid函數
print('*' * 25 + "Sigmoid函數" + "*" * 25)
m = nn.Sigmoid()
input = torch.randn(2)
print("原:", input)
print("結果:", m(input))
print('*' * 50)2.2 Tanh函數
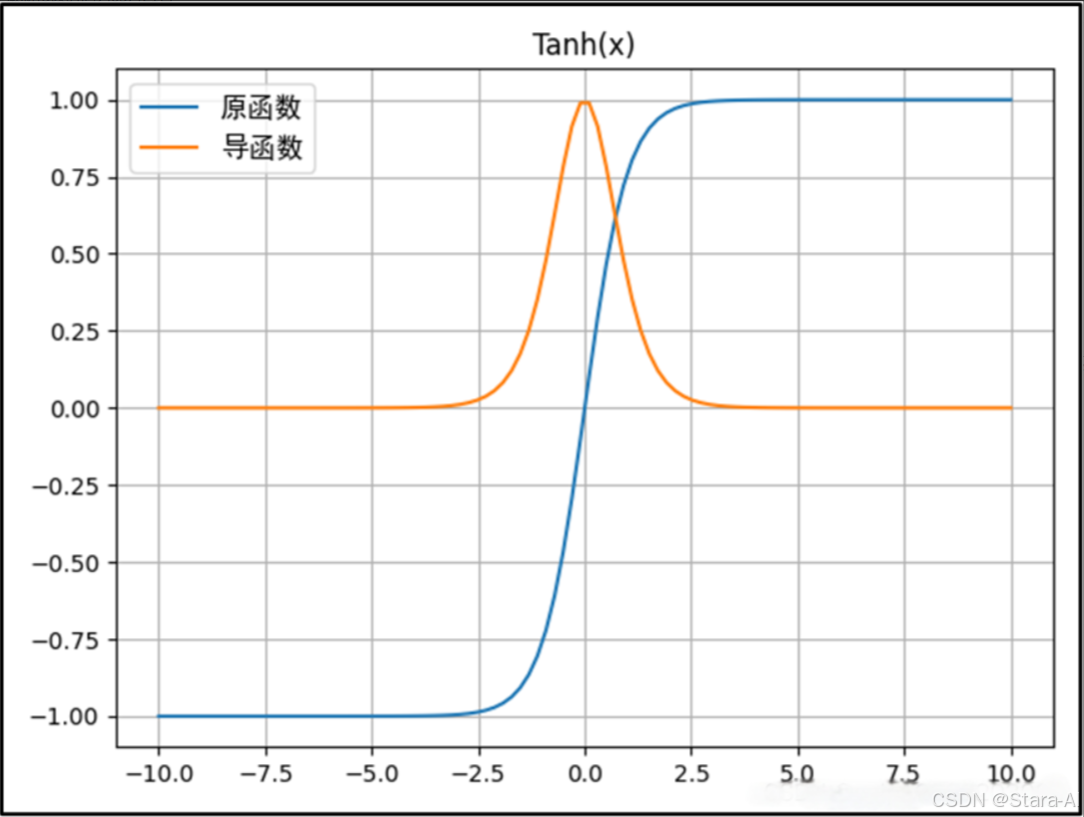
Tanh函數的公式: f(x)=ex?e?xex+e?xf(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}f(x)=ex+e?xex?e?x?Tanh函數的導函數: f′(x)=4(ex+e?x)2=1?[f(x)]2f'(x) = \frac{4}{(e^x + e^{-x})^2} = 1 - [f(x)]^2f′(x)=(ex+e?x)24?=1?[f(x)]2
優點:
- 在分類任務中,雙曲正切函數(Tanh)逐漸取代 Sigmoid 函數作為標準的激活函數,其具有很多神經網絡所鐘愛的特征。它是完全可微分的,反對稱,對稱中心在原點。
- 輸出是S型曲線,具備打破網絡層與網絡層之間的線性關系。負輸入將被強映射為負,而零輸入被映射為接近零;
tanh的輸出間隔為1且值域是以0為中心的[-1,1]。 - 在一般的二元分類問題中,tanh 函數用于隱藏層,而 sigmoid 函數用于輸出層,但這并不是固定的,需要根據特定問題進行調整。
不足:
- 當輸入較大或較小時,輸出幾乎是平滑的并且梯度較小,這不利于權重更新。
- Tanh函數也需要進行指數運算,所以其也會存在計算復雜度高且計算量大的問題。
- 當神經網絡的層數增多的時候,由于在進行反向傳播的時候,鏈式求導,多項相乘,函數進入飽和區(導數接近于零的地方)就會逐層傳遞,這種現象被稱為梯度消失。
Pytorch代碼:
import torch
import torch.nn as nn# Tanh函數
print('*' * 25 + "Tanh函數" + "*" * 25)
m = nn.Tanh()
input = torch.randn(2)
print("原:", input)
print("結果:", m(input))
print('*' * 50)2.3 ReLU 函數
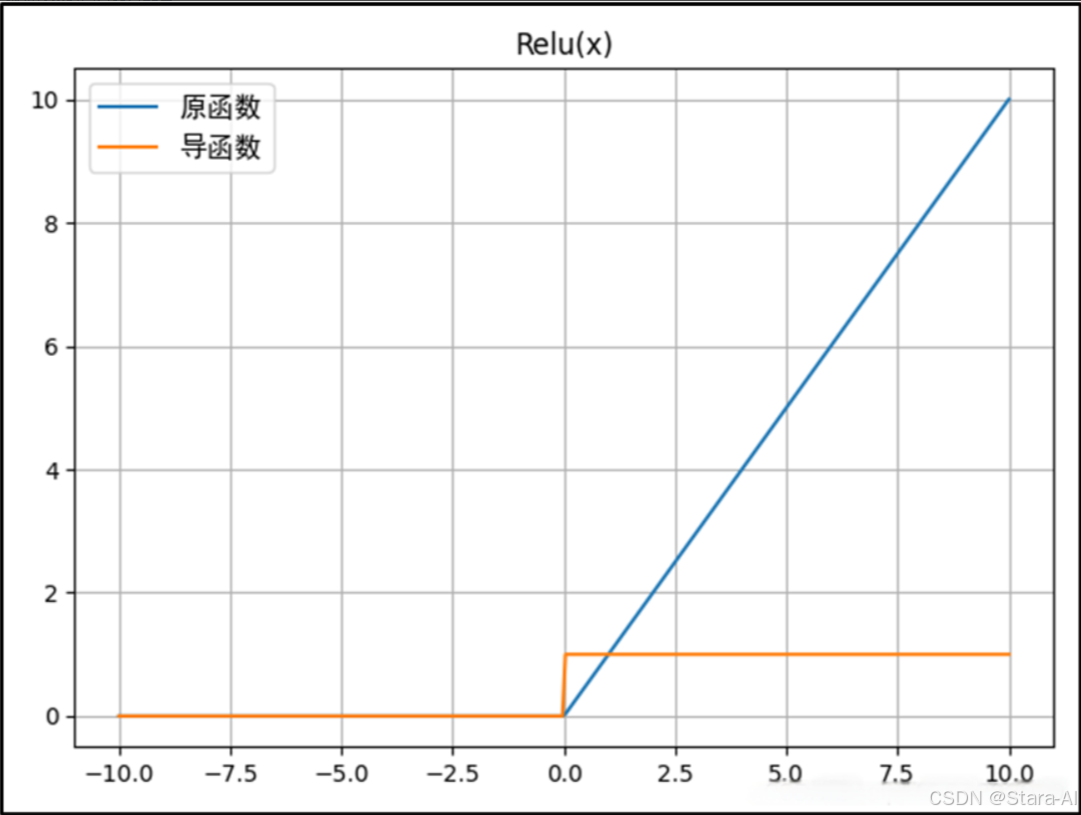
ReLU函數的公式: f(x)={x,x≥00,x<0f(x) = \begin{cases} x, & x \geq 0 \\ 0, & x < 0 \end{cases}f(x)={x,0,?x≥0x<0?ReLU函數的導函數: f′(x)={1,x≥00,x<0f'(x) = \begin{cases} 1, & x \geq 0 \\ 0, & x < 0 \end{cases}f′(x)={1,0,?x≥0x<0?
優點:
ReLU函數在正輸入時是線性的,收斂速度快,計算速度快,同時符合恒等性的特點。當輸入為正時,由于導數是1,能夠完整傳遞梯度,不存在梯度消失的問題(梯度飽和問題)。- 計算速度快。
ReLU函數中只存在線性關系且無論是函數還是其導數都不包含復雜的數學運算,因此它的計算速度比sigmoid和tanh更快。 - 當輸入大于0時,梯度為1,能夠有效避免鏈式求導法則梯度相乘引起的梯度消失和梯度爆炸;計算成本低。
- 當輸入為正的時候,導數不為零,從而允許基于梯度的學習(盡管在
x=0的時候,導數是未定義的)。當輸入為負值的時候,ReLU 的學習速度可能會變得很慢,甚至使神經元直接無效,因為此時輸入小于零而梯度為零。
不足:
ReLU的輸入值為負的時候,輸出始終為0,其一階導數也始終為0,這樣會導致神經元不能更新參數,也就是神經元不學習了,這種現象叫做“Dead Neuron”。為了解決ReLU函數這個缺點,在ReLU函數的負半區間引入一個泄露(Leaky)值,所以稱為Leaky ReLU函數。- 與
Sigmoid一樣,其輸出不是以0為中心的(ReLU的輸出為0或正數)。 ReLU在小于0的時候梯度為零,導致了某些神經元永遠被抑制,最終造成特征的學習不充分;這是典型的Dead ReLU問題,所以需要改進隨機初始化,避免將過多的負數特征送入ReLU。
Pytorch代碼:
import torch
import torch.nn as nn# Relu函數
print('*' * 25 + "Relu函數" + "*" * 25)
m = nn.ReLU()
input = torch.randn(2)
print("原:", input)
print("結果:", m(input))
print('*' * 50)2.4 Leaky ReLU函數
Leaky ReLU函數的公式: f(x)={x,x≥0λx,x<0,?λ∈(0,1)f(x) = \begin{cases} x, & x \geq 0 \\ \lambda x, & x < 0 \end{cases},\ \lambda \in (0,1)f(x)={x,λx,?x≥0x<0?,?λ∈(0,1)Leaky ReLU函數的導函數: f′(x)={1,x≥0λ,x<0,?λ∈(0,1)f'(x) = \begin{cases} 1, & x \geq 0 \\ \lambda, & x < 0 \end{cases},\ \lambda \in (0,1)f′(x)={1,λ,?x≥0x<0?,?λ∈(0,1)
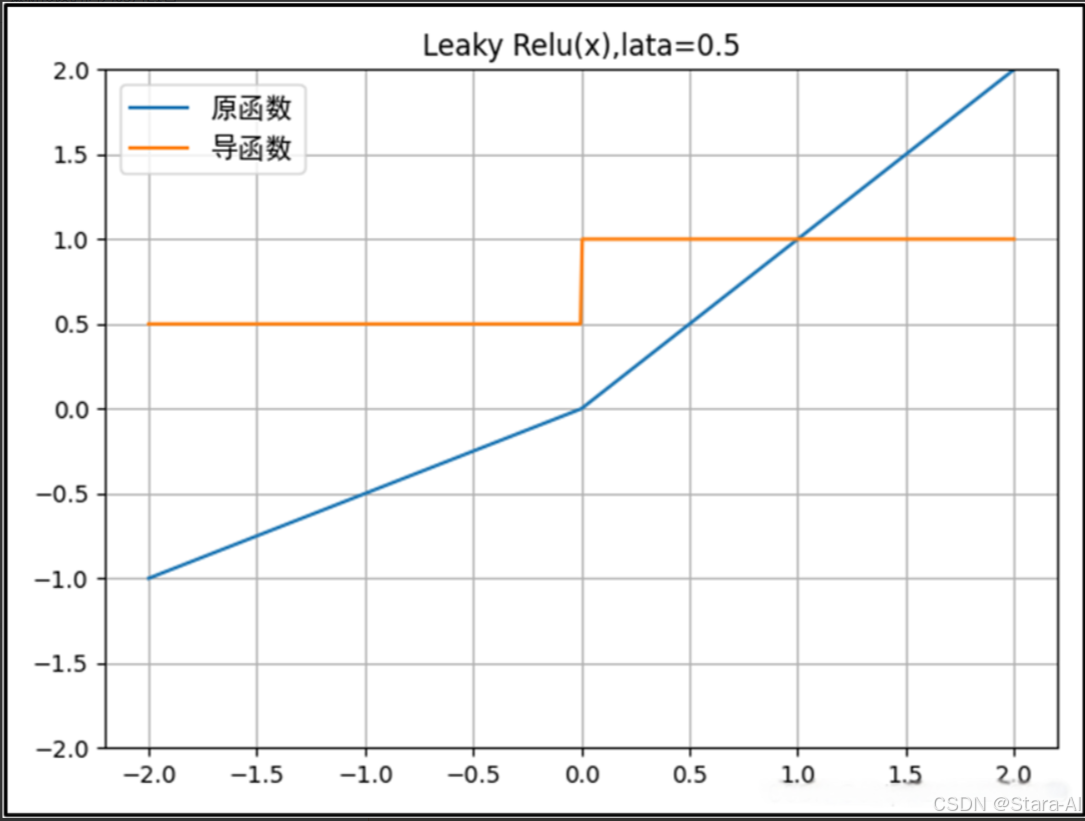
Leaky ReLU函數(ReLU的改進):
-
與ReLU函數相比,Leaky ReLU給負輸入添加了一個非常小的線性分量(如0.01x),以緩解負值區域梯度為零的問題;這有助于擴展ReLU函數的適用范圍,通常超參數𝜆的值設為0.01左右;其輸出范圍為負無窮到正無窮。
-
Leaky ReLU激活函數通過在負半軸引入一個較小的正斜率(例如𝜆=0.01),使得負輸入時仍有一定梯度,避免信息完全丟失,從而解決ReLU的“神經元死亡”(Dead ReLU)問題。該斜率𝜆為人為設定的超參數,一般取0.01。這樣可確保在模型訓練過程中,即使輸入小于0,神經元的權重仍能被更新。
-
Leaky ReLU不會出現Dead ReLU問題,但在深層網絡中仍可能面臨梯度爆炸的風險,尤其是在網絡較深或初始化不當的情況下。因此,必要時可結合使用具有飽和特性的激活函數(如
Sigmoid或Tanh)進行輸出層設計,或配合梯度裁剪、權重初始化等技術來提升訓練穩定性。
Leaky ReLU不足:
-
Leaky ReLU 是經典且廣泛使用的 ReLU 激活函數的一種變體,其特點是對負值輸入引入一個很小的非零斜率(例如 0.01)。由于其導數在負半軸不為零,能夠有效緩解“神經元靜默”(即 Dead ReLU)問題,從而允許梯度在反向傳播中持續流動,支持基于梯度的學習,盡管在負區域的學習速度較慢。
-
從理論上講,Leaky ReLU 保留了 ReLU 的計算高效性和非線性特性,同時避免了神經元因梯度為零而永久失效的問題,因此不會出現 Dead ReLU 現象。然而,在實際應用中,Leaky ReLU 并未被一致證明在所有任務和網絡結構中都優于標準 ReLU,其性能提升依賴于具體場景、超參數選擇和模型結構,因此是否使用仍需根據實驗效果權衡。
Pytorch代碼:
import torch
import torch.nn as nn# Leaky Relu函數
print('*' * 25 + "Leaky Relu函數" + "*" * 25)
m = nn.LeakyReLU(negative_slope=0.1) # negative_slope是個常數
input = torch.randn(2)
print("原:", input)
print("結果:", m(input))
print('*' * 50)
2.5 PReLU 函數
PReLU函數的公式: f(x)={x,x≥0αx,x<0,?(α是可訓練參數)f(x) = \begin{cases} x, & x \geq 0 \\ \alpha x, & x < 0 \end{cases},\ (\alpha\text{是可訓練參數})f(x)={x,αx,?x≥0x<0?,?(α是可訓練參數)PReLU函數的導函數: f′(x)={1,x≥0α,x<0,?(α是可訓練參數)f'(x) = \begin{cases} 1, & x \geq 0 \\ \alpha, & x < 0 \end{cases},\ (\alpha\text{是可訓練參數})f′(x)={1,α,?x≥0x<0?,?(α是可訓練參數)
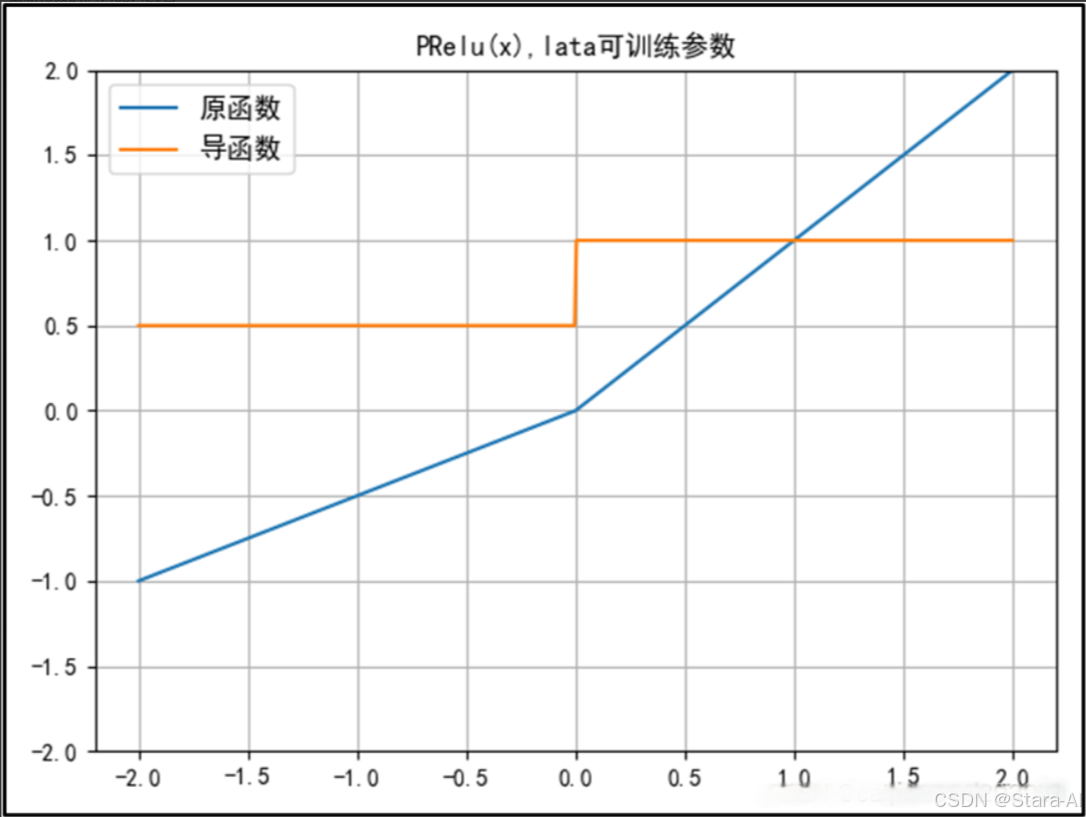
PReLU 函數( ReLU 的改進):
- 在負值域,
PReLU的斜率較小,這也可以避免Dead ReLU問題。與ELU相比,PReLU在負值域是線性運算。盡管斜率很小,但不會趨于0。 - 公式與Leaky ReLu相似,但并不完全一樣。
𝛼可以是常數,或自適應調整的參數。也就是說,如果讓 a 自適應,那么 PReLu 會在反向傳播時更新參數a。 參數α通常為0到1之間的數字,并且通常相對較小。- (1)如果
𝛼 = 0,則f(x)變為ReLU。?
(2)如果𝛼 > 0,則f(x)變為leaky ReLU。?
(3)如果𝛼是可學習的參數,則f(x)變為PReLU。
Pytorch代碼:
import torch
import torch.nn as nn# PRelu函數
print('*' * 25 + "PRelu函數" + "*" * 25)
m = nn.PReLU(num_parameters=1) # num_parameters是個可訓練參數
input = torch.randn(2)
print("原:", input)
print("結果:", m(input))
print('*' * 50)
2.6 RReLU 函數
-
RReLU函數的公式: f(x)={x,x≥0αx,x<0f(x) = \begin{cases} x, & x \geq 0 \\ \alpha x, & x < 0 \end{cases}f(x)={x,αx,?x≥0x<0? -
RReLU函數的導函數: f′(x)={1,x≥0α,x<0f'(x) = \begin{cases} 1, & x \geq 0 \\ \alpha, & x < 0 \end{cases}f′(x)={1,α,?x≥0x<0?
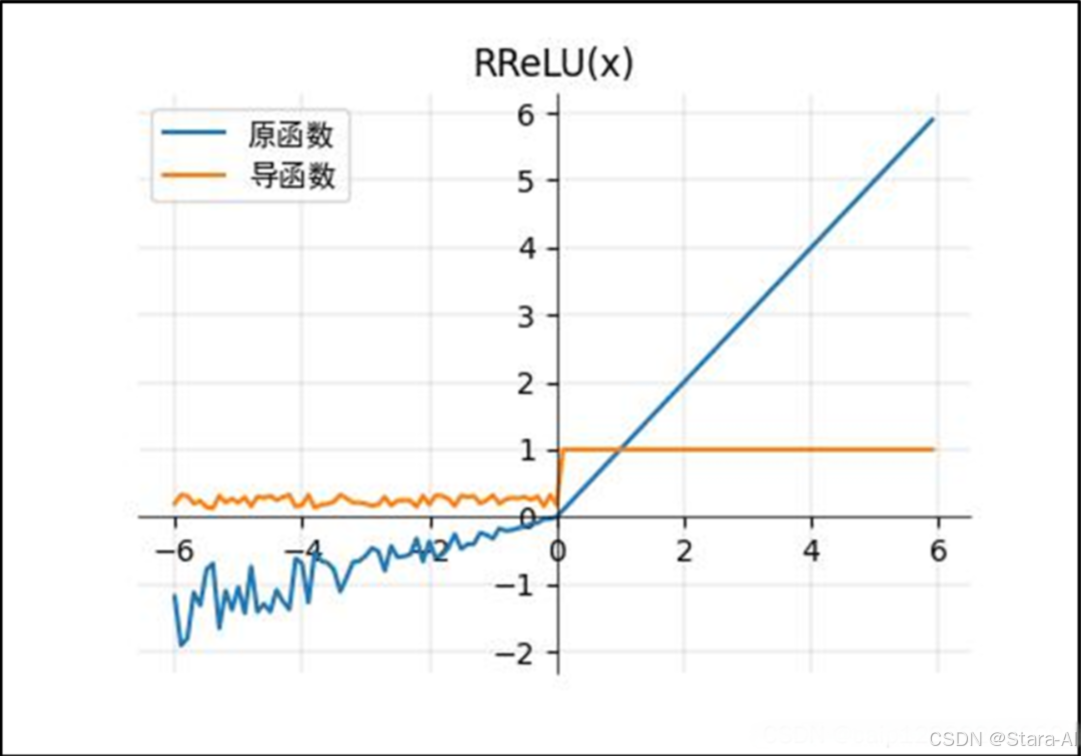
RReLU 函數( ReLU 的改進):
- RReLU 和 PReLU 的表達式一樣,但 𝛼 參數不一樣,這里的
𝛼是個隨機震蕩的數,范圍(pytorch):1/8~1/3。(對應圖的參數為lower =1/8,upper =1/3) - RReLU(隨機校正線性單元)。在 RReLU 中,
負部分的斜率在訓練中被隨機化到給定的范圍內,然后再測試中被固定。
Pytorch代碼:
import torch
import torch.nn as nn# RRelu函數
print('*' * 25 + "RRelu函數" + "*" * 25)
m = nn.RReLU(lower=0.1, upper=0.3) # 這里的參數屬于(lower,upper)之間的震蕩隨機數
input = torch.randn(2)
print("原:", input)
print("結果:", m(input))
print('*' * 50)
2.7 ELU函數
ELU函數的公式: f(x)={x,x≥0a(ex?1),x<0f(x) = \begin{cases} x, & x \geq 0 \\ a(e^x - 1), & x < 0 \end{cases}f(x)={x,a(ex?1),?x≥0x<0?ELU函數的導函數: f′(x)={1,x≥0aex,x<0f'(x) = \begin{cases} 1, & x \geq 0 \\ a e^x, & x < 0 \end{cases}f′(x)={1,aex,?x≥0x<0?
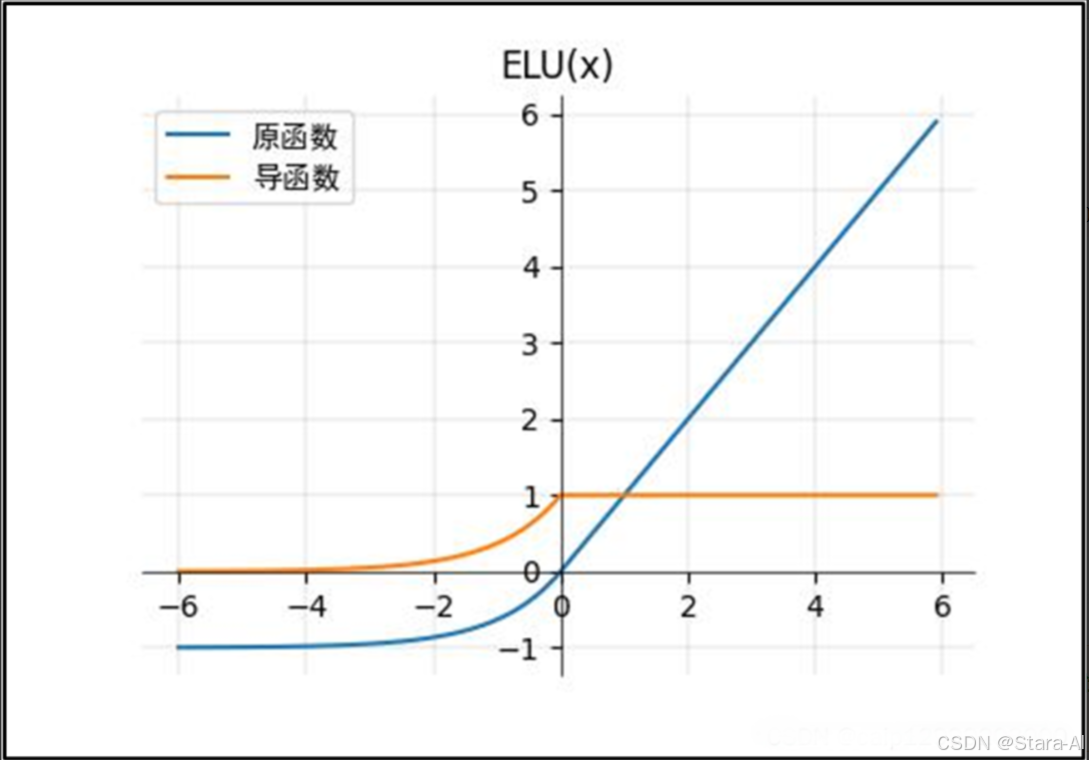
ELU 函數( ReLU 的改進):(上圖的 α 值為1.0):?
- ELU 在負值時是一個指數函數(使激活的平均值接近零),
具有軟飽和特性,對噪聲更魯棒,抗干擾能力強;在較小的輸入下會飽和至負值,從而減少前向傳播的變異和信息。 - 均值向零加速學習。
通過減少偏置偏移的影響,使正常梯度接近于單位自然梯度,可以使學習更快。 - 輸出有負值,
使得其輸出的平均值為0;右側的正值特性,可以像relu一樣緩解梯度消失的問題。
ELU 不足:?
ELu 也是為了解決 Dead ReLu 而提出的改進型。計算上稍微比 Leaky ReLu 復雜一點,但從精度看似乎并未提高多少。- 盡管理論上比 ReLU 要好,但目前在實踐中
沒有充分的證據表明 ELU 總是比 ReLU 好。
Pytorch代碼:
import torch
import torch.nn as nn# ELU函數
print('*' * 25 + "ELU函數" + "*" * 25)
m = nn.ELU(alpha=1.0) # 這里的參數alpha默認為1
input = torch.randn(2)
print("原:", input)
print("結果:", m(input))
print('*' * 50)
2.8 SELU函數
SELU函數的公式: f(x)={x,x>0α(ex?1),x≤0f(x) = \begin{cases} x, & x > 0 \\ \alpha(e^x - 1), & x \leq 0 \end{cases}f(x)={x,α(ex?1),?x>0x≤0?SELU函數的導函數: f′(x)={λ,x>0λαex,x≤0f'(x) = \begin{cases} \lambda, & x > 0 \\ \lambda \alpha e^x, & x \leq 0 \end{cases}f′(x)={λ,λαex,?x>0x≤0?
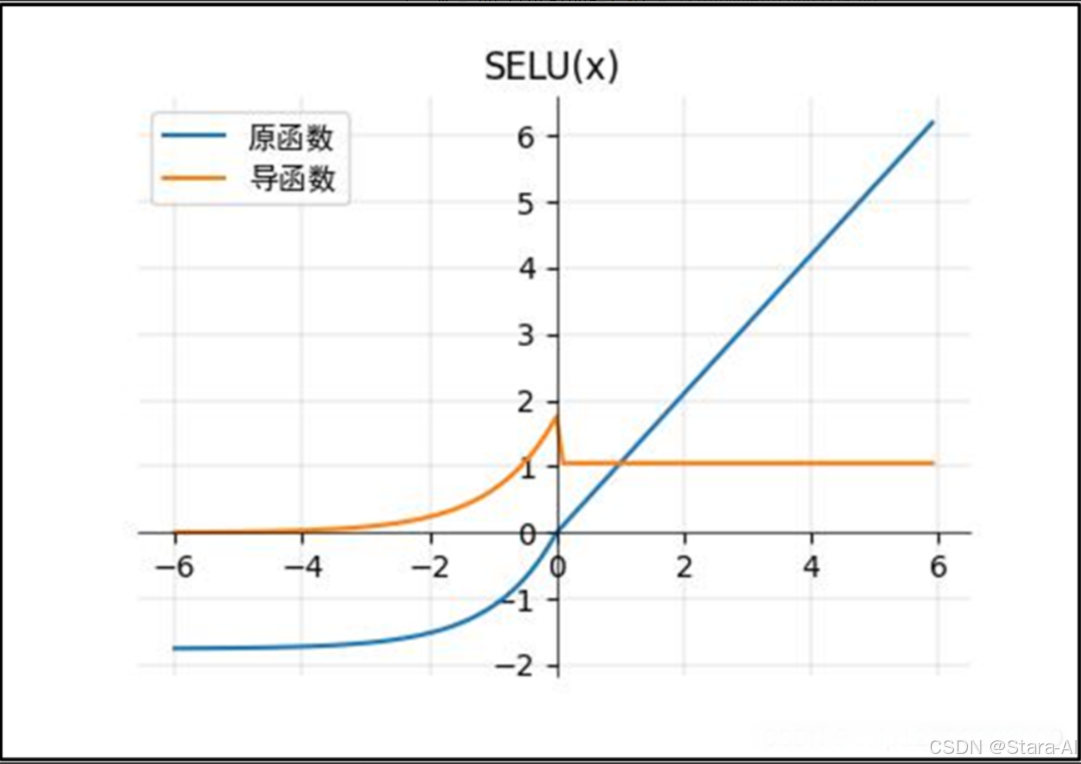
SELU函數(ReLU的改進):(上圖的𝛼=1.67 and 𝝀=1.05.)?:
- 當其中參數α=1.67 , λ=1.05時,在網絡權重服從正態分布的條件下,
各層輸出的分布會向標準正態分布靠攏。這種自我標準化的特性可以避免梯度消失和爆炸。 - SELU激活函數是在自歸一化網絡中定義的,
通過調整均值和方差來實現內部的歸一化,這種內部歸一化比外部歸一化更快,這使得網絡收斂得更快。 - SELU是給ELU乘上一個系數,該系數大于1。在這篇paper Self-Normalizing Neural Networks中,作者提到,SELU可以使得輸入在經過一定層數之后變為固定的分布。以前的ReLU、P-ReLU、ELU等激活函數都是在負半軸坡度平緩,
這樣在激活的方差過大時可以讓梯度減小,防止了梯度爆炸,但是在正半軸其梯度簡答的設置為了1。而SELU的正半軸大于1,在方差過小的時候可以讓它增大,但是同時防止了梯度消失。這樣激活函數就有了一個不動點,網絡深了之后每一層的輸出都是均值為0,方差為1。
pytorch代碼:
import torch
import torch.nn as nn# SELU函數
print('*' * 25 + "SELU函數" + "*" * 25)
m = nn.SELU() # 這里的參數默認alpha=1.67,scale=1.05
input = torch.randn(2)
print("原:", input)
print("結果:", m(input))
print('*' * 50)2.9 Softmax函數
Softmax 函數的公式: f(x)=exi∑i=0nexif(x) = \frac{e^{x_i}}{\sum_{i=0}^{n} e^{x_i}}f(x)=∑i=0n?exi?exi??
這里使用梯度無法求導,所以導函數圖像是一個 y=0 的直線。
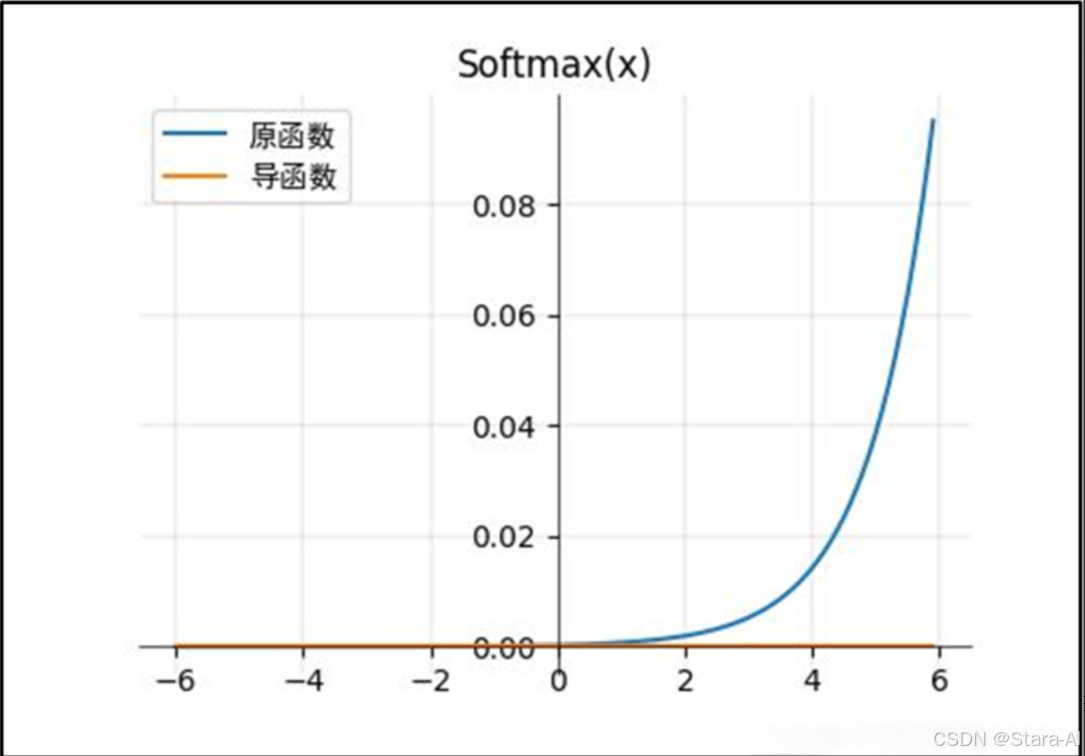
Softmax 激活函數的特點:
- 在零點不可微,負輸入的梯度為零,
這意味著對于該區域的激活,權重不會在反向傳播期間更新。? - 將預測結果轉化為非負數、預測結果概率之和等于1。?
- 經過使用指數形式的
Softmax函數能夠將差距大的數值距離拉的更大。在深度學習中通常使用反向傳播求解梯度進而使用梯度下降進行參數更新的過程,而指數函數在求導的時候比較方便。
Softmax不足:
使用指數函數,當輸出值非常大的話,計算得到的數值也會變的非常大,數值可能會溢出。
Pytorch代碼:
import torch
import torch.nn as nnprint('*' * 25 + "Softmax函數" + "*" * 25)
m = nn.Softmax(dim=0) # 維度為0
input = torch.randn(2)
print("原:", input)
print("結果:", m(input))
print('*' * 50)
2.10 Mish 函數
Mish 函數的公式: f(x)=x?tanh?(ln?(1+ex))f(x) = x \cdot \tanh(\ln(1 + e^x))f(x)=x?tanh(ln(1+ex))
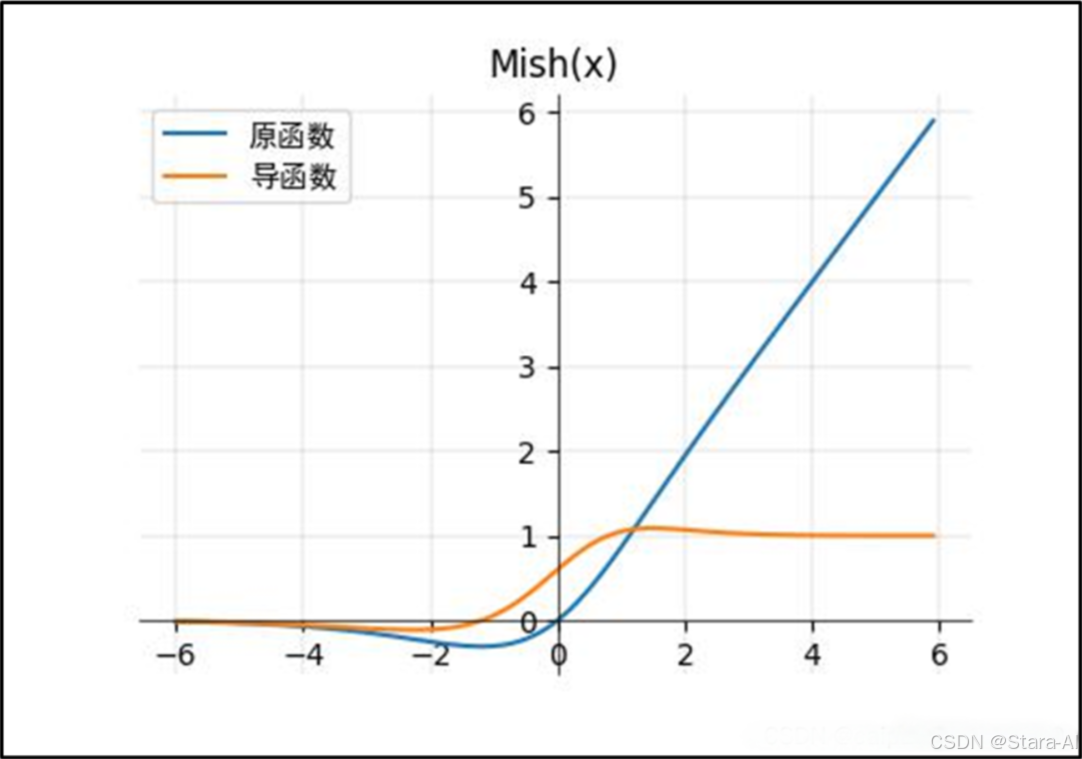
Mish 優點:
Mish激活函數無邊界(即正值可以達到任何高度)避免了由于封頂而導致的飽和。理論上對負值的輕微允許允許更好的梯度流,而不是像 ReLU 中那樣的硬零邊界。平滑的激活函數允許更好的信息深入神經網絡,從而得到更好的準確性和泛化。
Mish 函數具有的特點:
- 無上界有下界,這樣可以保證沒有飽和區域,因此在訓練過程中不會有梯度消失的問題,這個和relu后面的激活函數一樣。
有下限的話能夠保證具有一定的regularization effect,這對于神經網絡訓練來說是一個很好的特性。? - 非單調性函數,輸入較小負數的時候往往梯度回傳也會很小,
這樣會導致收斂較慢,但是如果輸入較大負數的時候不縮小的話,又容易梯度爆炸。這種性質有助于小的負值,從而穩定網絡梯度流。? - 無窮階連續性和光滑性,Mish函數是光滑函數,
具有較好的泛化能力和結果的有效優化能力,可以提高結果的質量。
3. 繪制激活函數
import torch
import numpy as np
import matplotlib.pylab as plt
import sys
from matplotlib import pyplot as plt
from IPython import display
from matplotlib import style
from torch.nn.modules.module import Module
from torch.nn import functional as F
from torch import Tensordef xyplot(x_vals, y_vals, name):plt.rcParams['figure.figsize'] = (5, 3.5)plt.grid(c='black', linewidth=0.08)plt.plot(x_vals.detach().numpy(), y_vals.detach().numpy(), label=name, linewidth=1.5)font = {'family': 'SimHei'}; # 中文字體plt.legend(loc='upper left', prop=font)# dark_background, seaborn, ggplot# plt.style.use("seaborn")ax = plt.gca()ax.spines['right'].set_color("none")ax.spines['top'].set_color("none")ax.spines['bottom'].set_position(("data", 0))ax.spines['left'].set_position(("data", 0))ax.spines['bottom'].set_linewidth(0.5)ax.spines['left'].set_linewidth(0.5)ax.xaxis.set_ticks_position('bottom')ax.yaxis.set_ticks_position('left')# 激活函數以及導函數
def func_(y_func, func_n, save_=None, x_low=-6.0, x_top=6.0):x = torch.arange(-6.0, 6.0, 0.1, requires_grad=True)y = y_func(x)xyplot(x, y, '原函數')# 導數y.sum().backward()xyplot(x, x.grad, "導函數")plt.title(f"{func_n}(x)")if save_ is not None:plt.draw()plt.savefig(f"./{func_n}.jpg")plt.close()plt.show()# 由于我使用的pytorch版本沒有Mish函數,所以整了一個
class Mish(Module):__constants__ = ['beta', 'threshold']beta: intthreshold: intdef __init__(self, beta: int = 1, threshold: int = 20) -> None:super(Mish, self).__init__()self.beta = betaself.threshold = thresholddef forward(self, input: Tensor) -> Tensor:return input * torch.tanh(F.softplus(input, self.beta, self.threshold))def extra_repr(self) -> str:return 'beta={}, threshold={}'.format(self.beta, self.threshold)#
class Swish(Module):__constants__ = ['beta']beta: intdef __init__(self, beta: int = 1) -> None:super(Swish, self).__init__()self.beta = betadef forward(self, input: Tensor) -> Tensor:return input * torch.sigmoid(input * self.beta)# RReLU
func_(torch.nn.RReLU(), "RReLU", True)
# ELU
func_(torch.nn.ELU(), "ELU", True)
# SELU
func_(torch.nn.SELU(), "SELU", True)
# CELU
func_(torch.nn.CELU(), "CELU", True)
# GELU
func_(torch.nn.GELU(), "GELU", True)
# ReLU6
func_(torch.nn.ReLU6(), "ReLU6", True)
# Swish
func_(Swish(), "Swish", True)
# Hardswish
func_(torch.nn.Hardswish(), "Hardswish", True)
# SiLU
func_(torch.nn.SiLU(), "SiLU", True)
# Softplus
func_(torch.nn.Softplus(), "Softplus", True)
# Mish
func_(Mish(), "Mish", True)
# Softmax
func_(torch.nn.Softmax(), "Softmax", True)4. 總結
激活函數的發展體現了從“簡單有效”到“精細調控梯度流”的演進。現代深度學習中,ReLU及其變體、Swish、Mish、GELU 成為主流選擇,而 Sigmoid 和 Tanh 已逐步退出隱藏層舞臺。合理選擇激活函數,不僅能加速收斂,還能提升模型魯棒性與最終性能。
關鍵原則:
- 避免梯度消失/爆炸
- 保持梯度流動穩定
- 平衡表達能力與計算效率
- 匹配任務需求(分類/回歸)
掌握這些激活函數的數學形式、特性與適用場景,是構建高效神經網絡的基礎。
📊 選擇建議總結
| 場景 | 推薦激活函數 |
|---|---|
| 隱藏層通用選擇 | ReLU、Swish、Mish、GELU |
| 深層網絡防梯度消失 | ELU、SELU、Swish、Mish |
| 需要光滑/可微性 | Softplus、Mish、GELU |
| 自歸一化網絡 | SELU + Alpha Dropout |
| 二分類輸出層 | Sigmoid |
| 多分類輸出層 | Softmax |
| 回歸輸出層 | Identity |
| 輕量化模型 | Hard-Sigmoid、Hard-Swish |





等級考試試卷-實操題(2021年12月))












、自動目錄(修改字體類型)】)
)