- 什么是模擬?
是一種通過模仿現實世界或問題場景的運行過程來求解問題的算法思想。它不依賴復雜的數學推導或邏輯優化,而是按照問題的實際規則、步驟或流程,一步步地 “復現” 過程,最終得到結果。
使用場景:
當問題的邏輯規則明確、步驟可分解,且難以用數學公式直接求解時,模擬算法是直觀有效的選擇。常見場景包括:
過程性問題:如交通流量模擬、電梯運行調度、銀行排隊系統等;
規則性問題:如模擬棋牌游戲(圍棋、撲克)的出牌邏輯、模擬電路時序等;
數值計算模擬:如天氣預報中的大氣環流模擬、物理實驗中的粒子運動模擬等。
總結:
模擬算法是一種 “按部就班” 的求解思路,通過復現問題的實際過程得到結果,適合規則明確、步驟可模擬的場景。它的優勢在于直觀和易實現,缺點是在大規模問題中可能效率較低,需根據具體場景權衡使用。
一. (1576.) 替換所有的問號

解法:
要求不能包含連續的重復字符,根據題目模擬,從前往后遍歷整個字符串,找到問號之后就用a~z的每一個字符去嘗試替換
class Solution
{
public:string modifyString(string s) {int n = s.size();for(int i = 0; i < n; i++){if(s[i] == '?') // 替換{for(char ch = 'a'; ch <= 'z'; ch++){if((i == 0 || ch != s[i - 1]) && (i == n - 1 || ch != s[i
+ 1]))//巧妙的判斷了頭尾邊界情況,不是邊界情況時要滿足i位置字符與左右兩邊不同{s[i] = ch;break;}}}}return s;}
};
二. (495.) 提莫攻擊

模擬 + 分情況討論。
計算相鄰兩個時間點的差值:
i. 如果差值?于等于中毒時間,說明上次中毒可以持續 duration 秒;
ii. 如果差值?于中毒時間,那么上次的中毒只能持續兩者的差值。
注意:最后一次中毒時間要全部加上,因為沒法與后一個元素計算差值
class Solution {
public:int findPoisonedDuration(vector<int>& t, int d) {int ret=0;for(int i=1;i<t.size();i++){int add=t[i]-t[i-1];//判斷要增加的秒數if(add<d) ret+=add;else ret+=d;}//處理最后一個元素,秒數全部加上ret+=d;return ret;}
};
三. (6.) N 字形變換

算法原理:
- 解法1:模擬
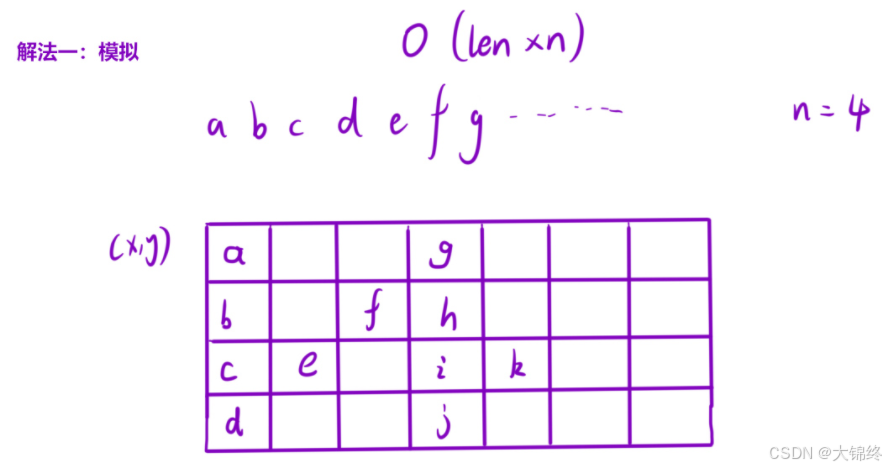
直接利用坐標規律填入數據,形成新字符串時也要再遍歷一遍數組,總共需要兩次,時間復雜度和空間復雜度都一樣有點高
- 解法2:找規律
可以先通過具體行數的一個例證找到一種規律,再通過不同行數的例子來驗證是否正確。
通過行數為4的情況來找規律
1.利用原字符串下標來進行找規律,就不需要遍歷數組,直接在原字符串中操作添加到新字符串來提高效率。圖中數組是為了方便找規律,不加入實際代碼中
2.列數小于原字符串大小就夠用,計算每一行元素之間的公差,找到規律并驗證
3.第一行和最后一行的處理情況相同,中間行元素要兩個兩個一起遞增相加
4.注意當行數等于1時的特殊情況,直接返回原字符串,避免進入死循環(公差為0)
class Solution {
public:string convert(string s, int n) {//處理特殊情況if(n==1) return s;//公差int d=2*n-2;string ret;//處理第一行元素for(int i=0;i<s.size();i+=d) ret+=s[i];//處理中間行元素for(int i=1;i<n-1;i++)//遍歷中間每一行{for(int k=i,j=d-i;k<s.size()||j<s.size();k+=d,j+=d){//||保證有一個元素在范圍內,添加時要先進性判斷if(k<s.size()) ret+=s[k];if(j<s.size()) ret+=s[j];}}//處理最后一行元素for(int i=n-1;i<s.size();i+=d) ret+=s[i];return ret;}
};
四. (38.) 外觀數列
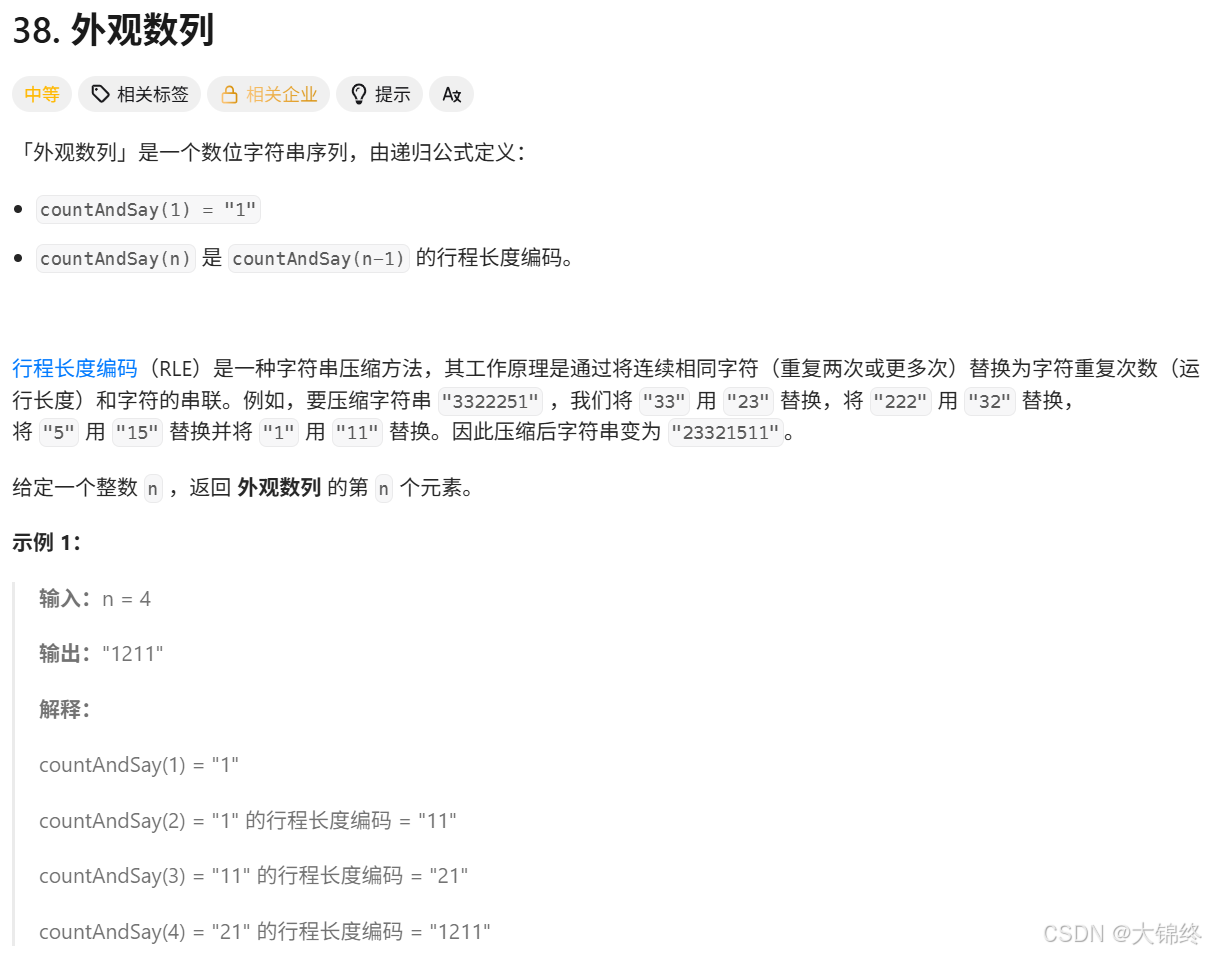
解法:
利用雙指針,開始都指向頭位置,一個移動另一個不動,元素相等時后移直到不等時停止,計算差值即為不動指針所對應的元素個數,然后更新不動指針,如此循環往復
class Solution {
public:string countAndSay(int n) {string ret="1";for(int i=1;i<n;i++)// 解釋 n - 1 次 ret 即可{string tmp;//用于記錄下一項的臨時變量,ret為當前解析的字符串int len=ret.size();int count=1;//統計連續相同字符的個數,最少出現一次for(int left=0,right=0;right<len;){// 移動right,找到與ret[left]不同的第一個位置while(right<len&&ret[left]==ret[right]) right++;count=right-left;// 拼接:"連續的個數" + "字符本身"tmp+=to_string(count)+ret[left];// 移動left到right的位置,開始統計下一組連續字符left=right;}ret=tmp;}return ret;}
};
解析:
得到外觀數列第n項的結果,只需要解析前n-1項即可。第一項一定為1,所以從1開始解析,創建一個變量tmp來存儲解析后作為下一次解析的字符串。內層循環中通過雙指針遍歷當前項,解析完后更新當前項,繼續迭代下去
注意:
1.初始化方式完全不同
string ret=“1”:
是包含單個字符 ‘1’ 的字符串,ret.size() 為 1,ret[0] 為 ‘1’(ASCII 碼值為 49)。
string ret{1}:
此時會調用 std::string 的另一個構造函數:string(size_t n, char c),該構造函數的含義是 “創建一個包含 n 個字符 c 的字符串”。 1 會被隱式轉換為size_t 類型(無符號整數),作為第一個參數(字符個數),整數 1 會被當作 char 類型的 ASCII 碼值,即 string ret{1}; 等價于 string ret(1, ‘\x01’),其中 ‘\x01’ 是 ASCII 碼為 1 的控制字符(SOH,標題開始符)
這樣初始化的結果是一個長度為 1 的字符串,但包含的字符是 ASCII 碼為 1 的不可見控制字符(而非字符 ‘1’),ret[0] 的值為 1(十進制),而非 49。
本質:用整數對應的ASCII 碼值初始化,字符串內容是該 ASCII 碼對應的字符(通常是不可見的控制字符)。
2.字符串拼接邏輯
std::string的operator+=支持以下常見形式:
追加單個字符:ret += ‘a’
追加字符串:ret += “abc” 或 ret += another_str
不支持ret += {str1, str2}這種初始化列表形式,整數轉為字符串要加to_string()
五. (1419.) 數?蛙

解法:

? 當遇到 ‘r’ ‘o’ ‘a’ ‘k’ 這四個字符的時候,我們要去看看每?個字符對應的前驅字符,
有沒有?蛙叫出來。如果有?蛙叫出來,那就讓這個?蛙接下來喊出來這個字符;如果沒有,直接返回 -1 ;
? 當遇到 ‘c’ 這個字符的時候,我們去看看 ‘k’ 這個字符有沒有?蛙叫出來。如果有,就讓這個?蛙繼續去喊 ‘c’ 這個字符;如果沒有的話,就重新搞?個?蛙。
- if-else方法
完全模擬上圖過程即可,只需注意返回值時的多種情況
class Solution {
public:int minNumberOfFrogs(string croakOfFrogs) {int c=0,r=0,o=0,a=0,k=0;for(auto ch:croakOfFrogs){if(ch=='c'){if(k!=0){k--;c++;}else c++;}else if(ch=='r'){if(c!=0){c--;r++;}else return -1;}else if(ch=='o'){if(r!=0){r--;o++;}else return -1;}else if(ch=='a'){if(o!=0){o--;a++;}else return -1;}else if(ch=='k'){if(a!=0){a--;k++;}else return -1;}}//判斷一次完整的蛙叫都沒有if(k==0) return -1;//判斷c不能滿足一次蛙叫的情況,可以和除k以外的字符比較是否相等//不能和k比因為可以由一只蛙重復叫else if(c!=r) return -1;else return k;}
};
- 哈希表方法
class Solution {
public:int minNumberOfFrogs(string croakOfFrogs) {string t="croak";int n=t.size();vector<int>hash(n);//用數組模擬哈希表unordered_map<char,int>index;//為了方便查找下標for(int i=0;i<n;i++){index[t[i]]=i;}for(auto ch:croakOfFrogs){if(ch=='c'){if(hash[n-1]) {hash[n-1]--;hash[0]++;}else hash[0]++;}else{//其他情況都適用,避免了條件判斷int i=index[ch];//得到下標if(hash[i-1]==0) return -1;hash[i-1]--;hash[i]++; }}for(int i=0;i<n-1;i++){//判斷蛙叫是否有效,除k外必須都為0if(hash[i]) return -1;}return hash[n-1];}
};
適用于通用情況,當不知道給定字符串內容時適用,通過數組模擬哈希降低空間復雜度,再用哈希表存儲字符所對應的下標,方便查找。循環時只用分兩組,避免繁雜的情況討論
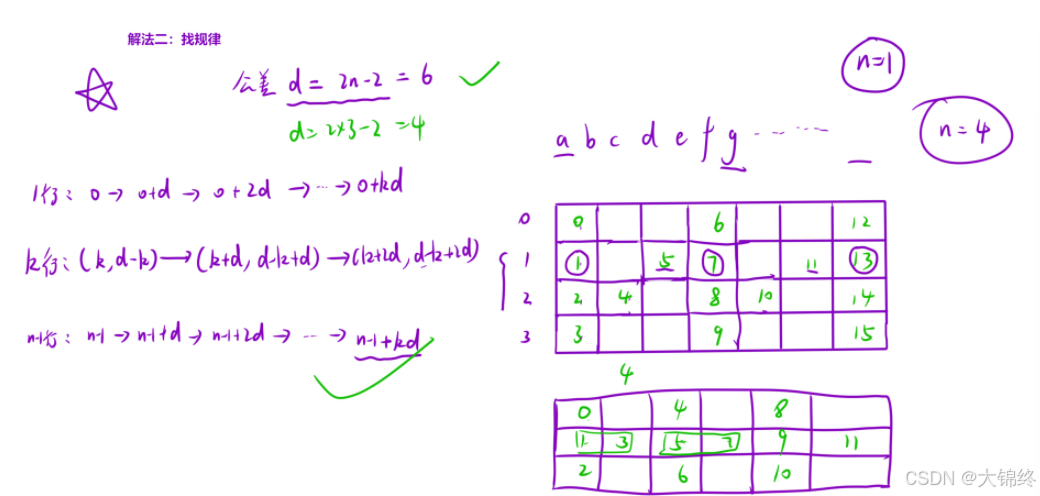


》免費中文翻譯 (第4章) --- Workflow: code style)

)







)
的數據回歸預測模型)
)




