1、紅黑樹的概念
????????紅黑樹,是一種二叉搜索樹,但在每個結點上增加一個存儲位表示結點的顏色,可以是Red或 Black。 通過對任何一條從根到葉子的路徑上各個結點著色方式的限制,紅黑樹確保沒有一條路 徑會比其他路徑長出倆倍,因而是接近平衡的。
紅黑樹圖像,如圖所示:
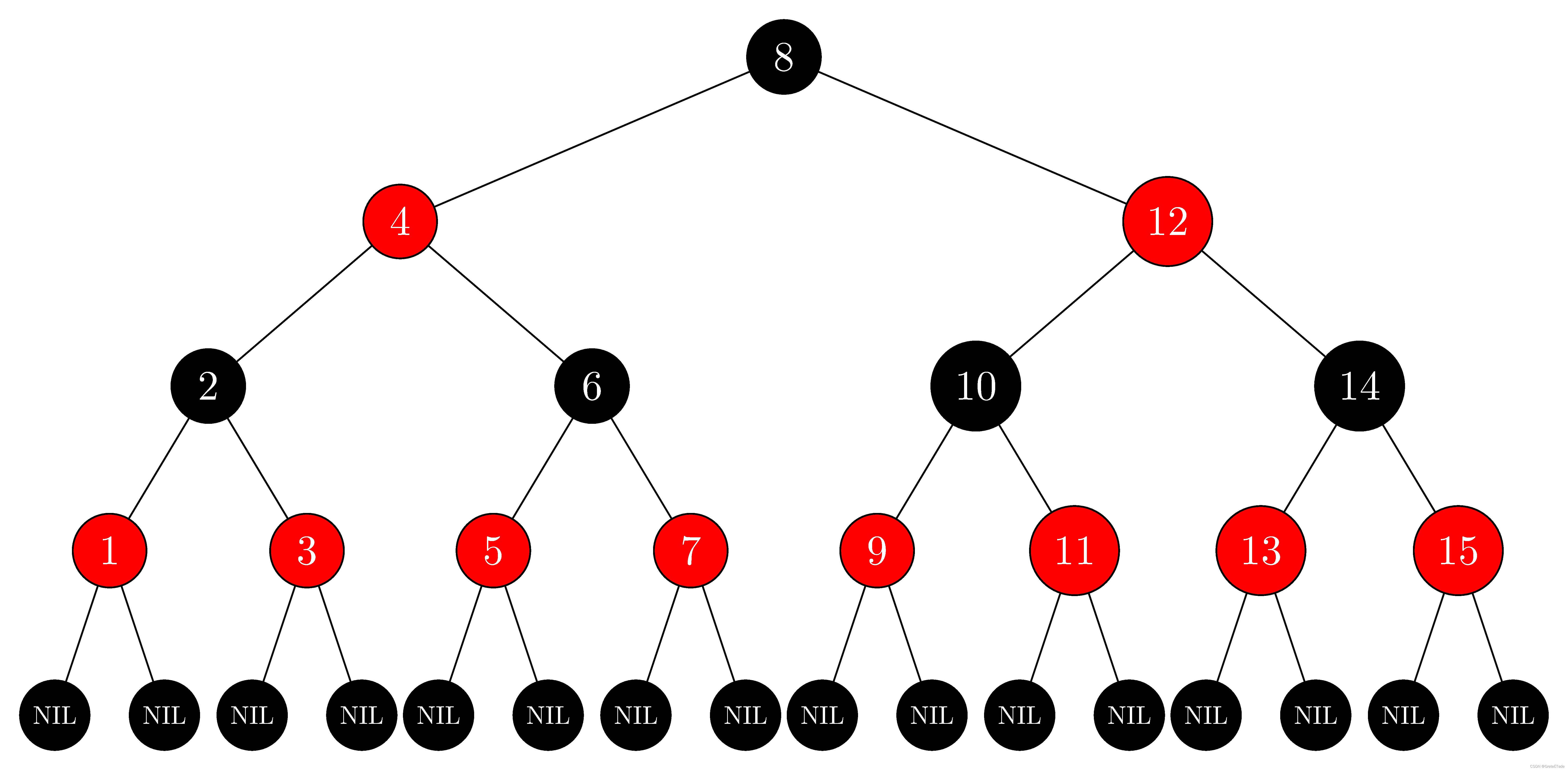
2、紅黑樹的性質
顏色屬性:每個節點不是紅色就是黑色
根節點屬性:根節點必須是黑色的
紅色節點屬性:如果一個節點是紅色的,則它的兩個子節點必須是黑色的(即不能有兩個連續的紅色節點)
黑色高度屬性:對于每個節點,從該節點到其所有后代葉節點的簡單路徑上,包含相同數目的黑色節點
葉子節點屬性:每個葉子節點(NIL節點,空節點)都是黑色的
????????這些性質保證了紅黑樹的關鍵特性:最長路徑不超過最短路徑的兩倍,從而保證了樹的平衡性。
3、紅黑樹的實現
1.節點結構定義
template<class T>
struct RBTreeNode {RBTreeNode<T>* _left; // 左子節點RBTreeNode<T>* _right; // 右子節點RBTreeNode<T>* _parent; // 父節點T _kv; // 鍵值對數據Colour _col; // 節點顏色(RED或BLACK)RBTreeNode(const T& kv):_left(nullptr), _right(nullptr), _parent(nullptr),_kv(kv), _col(RED) {}
};????????節點包含左右子節點指針、父節點指針、存儲的數據以及顏色標記。新節點默認為紅色。
2. 插入操作 (Insert)
????????功能:向紅黑樹中插入一個新節點,并保持紅黑樹的性質。
步驟:
如果樹為空,創建新節點作為根節點,并設為黑色
按照二叉搜索樹的規則找到插入位置
創建新節點(紅色)并插入到正確位置
檢查并修復紅黑樹性質:
如果父節點是黑色,無需處理
如果父節點是紅色,需要調整:
情況1:叔叔節點是紅色 - 變色處理
情況2:叔叔節點是黑色或不存在 - 旋轉處理
確保根節點始終為黑色
約定:cur為當前節點,p為父節點,g為祖父節點,u為叔叔節點
- 情況一: cur為紅,p為紅,g為黑,u存在且為紅
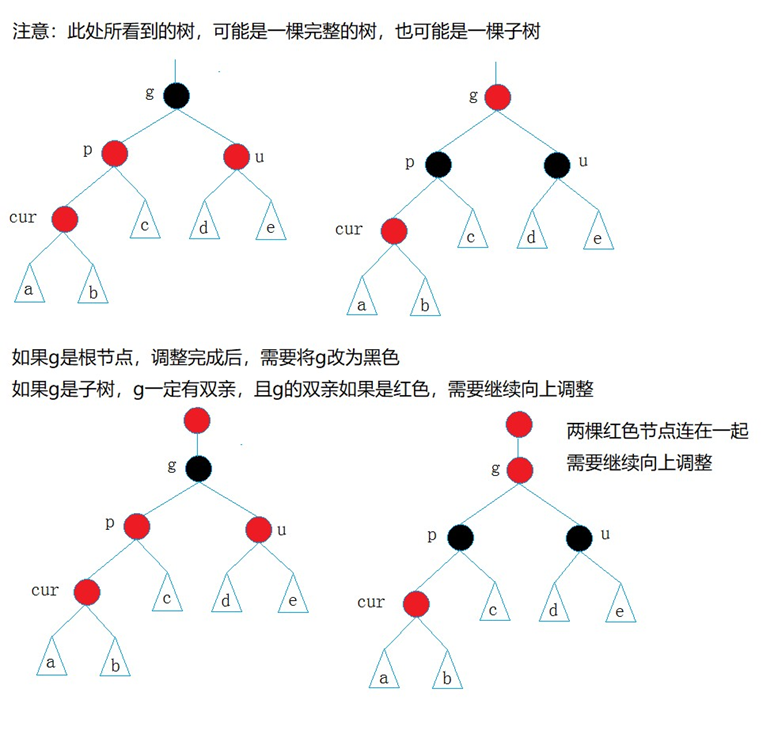
cur和p均為紅,違反了性質三,此處能否將p直接改為黑?
????????解決方式:將p,u改為黑,g改為紅,然后把g當成cur,繼續向上調整。
- 情況二: cur為紅,p為紅,g為黑,u不存在/u存在且為黑
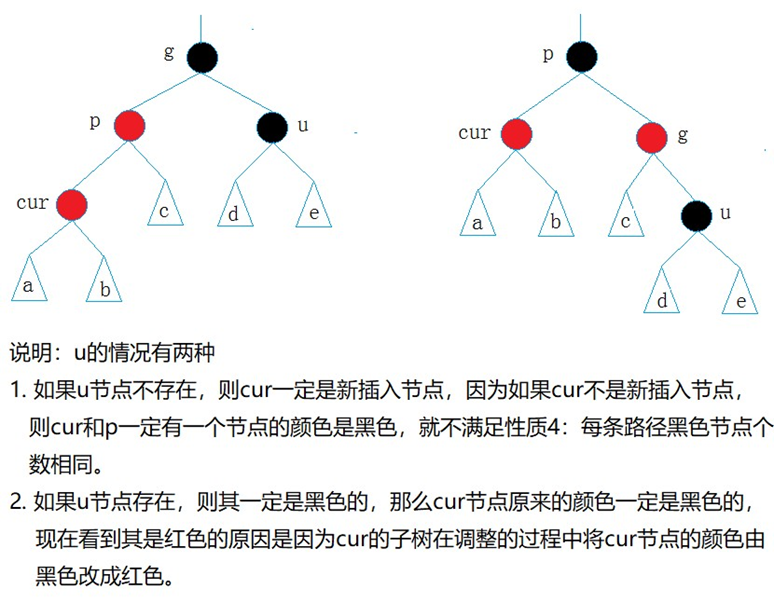
p為g的左孩子,cur為p的左孩子,則進行右單旋轉;
相反, p為g的右孩子,cur為p的右孩子,則進行左單旋轉
p、g變色--p變黑,g變紅
- 情況三: cur為紅,p為紅,g為黑,u不存在/u存在且為黑
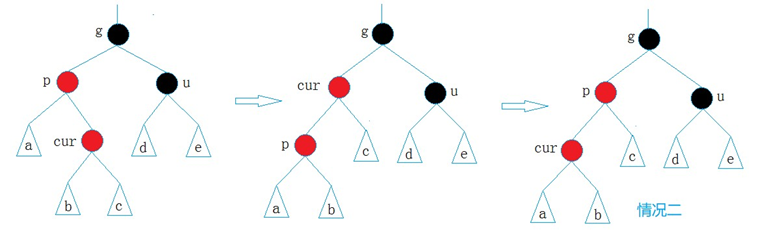
p為g的左孩子,cur為p的右孩子,則針對p做左單旋轉;
相反, p為g的右孩子,cur為p的左孩子,則針對p做右單旋轉
則轉換成了情況2
針對每種情況進行相應的處理即可。
bool Insert(const T& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//u存在且為紅if (uncle && uncle->_col == RED){//變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//繼續向上處理cur = grandfather;parent = cur->_parent;}else //u不存在或存在且為黑{if (cur == parent->_left){// g// p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else // parent == grandfather->_right{Node* uncle = grandfather->_left;//u存在且為紅if (uncle && uncle->_col == RED){//變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//繼續向上處理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){// g// p// cRotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{// g// p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;
}
3. 左旋操作 (RotateL)
????????功能:以parent節點為支點進行左旋。
操作:
將cur的左子節點作為parent的右子節點
將parent作為cur的左子節點
更新各個節點的父指針
處理根節點情況
//左單旋
void RotateL(Node* parent)
{Node* cur = parent->_right;parent->_right = cur->_left;if (cur->_left){cur->_left->_parent = parent;}cur->_left = parent;Node* pparent = parent->_parent;parent->_parent = cur;if (pparent == nullptr){_root = cur;cur->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = cur;}else if (pparent->_right == parent){pparent->_right = cur;}cur->_parent = pparent;}
}
4.右旋操作 (RotateR)
????????功能:以parent節點為支點進行右旋。
操作:
將cur的右子節點作為parent的左子節點
將parent作為cur的右子節點
更新各個節點的父指針
處理根節點情況
//右單旋
void RotateR(Node* parent)
{Node* cur = parent->_left;parent->_left = cur->_right;if (cur->_right){cur->_right->_parent = parent;}Node* pparent = parent->_parent;cur->_right = parent;parent->_parent = cur;if (pparent == nullptr){_root = cur;cur->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = cur;}else{pparent->_right = cur;}cur->_parent = pparent;}
}5. 紅黑樹驗證 (IsBalance)
功能:驗證紅黑樹是否滿足以下性質:
每個節點要么是紅色,要么是黑色
根節點是黑色
每個葉子節點(NIL節點)是黑色
不能有兩個連續的紅色節點
從任一節點到其每個葉子的所有路徑都包含相同數目的黑色節點
實現:
IsBalance()是公開接口,調用IsBalance(_root)
IsBalance(Node* root)驗證根節點是否為黑色
CheckColour()遞歸檢查:
計算每條路徑的黑色節點數是否一致
檢查是否有連續的紅色節點
bool CheckColour(Node* root, int blacknum, int benchmark)
{//遞歸停止條件if (root == nullptr){if (blacknum != benchmark)return false;return true;}if (root->_col == BLACK){++blacknum;}if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << root->_kv.first << "出現連續的紅色節點" << endl;return false;}return CheckColour(root->_left, blacknum, benchmark)&& CheckColour(root->_right, blacknum, benchmark);
}bool IsBalance()
{return IsBalance(_root);
}bool IsBalance(Node* root)
{if (root == nullptr)return true;if (root->_col != BLACK){return false;}//基準值int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)++benchmark;cur = cur->_left;}return CheckColour(root, 0, benchmark);
}
4、紅黑樹與AVL樹的比較
| 特性 | 紅黑樹 | AVL樹 |
|---|---|---|
| 平衡標準 | 近似平衡(最長路徑≤2倍最短) | 嚴格平衡(高度差≤1) |
| 查詢效率 | O(log n) | O(log n) |
| 插入/刪除效率 | 相對較高(旋轉次數少) | 相對較低(旋轉次數多) |
| 實現復雜度 | 中等 | 較高 |
| 適用場景 | 頻繁插入刪除的場景 | 查詢為主、很少修改的場景 |
5、 紅黑樹的應用
C++ STL:map、set、multimap、multiset
Java集合框架:TreeMap、TreeSet
Linux內核:進程調度、內存管理等
其他:數據庫索引、文件系統等
6、 總結
????????紅黑樹是一種高效的平衡二叉搜索樹,它通過顏色標記和旋轉操作維持樹的近似平衡。相比于AVL樹,紅黑樹在插入和刪除操作上更為高效,適合需要頻繁修改的場景。理解紅黑樹的原理和實現,對于深入掌握STL容器和許多系統級的數據結構都有重要意義。
?????????紅黑樹的設計體現了計算機科學中典型的時空權衡思想:通過放寬平衡條件來減少維護平衡的開銷,同時仍能保證較好的性能。這種思想在許多算法和數據結構中都有體現,值得深入理解和掌握。
)


)





)

)

:狀態管理)


)


