【感知機】感知機(perceptron)學習算法例題及詳解

感知機( perceptron )是二類分類的線性分類模型，其輸入為實例的特征向量，輸出為實例的類別，取+1 和-1二值。感知機對應輸入空間(特征空間)中將實例劃分為正負兩類的分離超平面，是一種判別模型。感知機是神經網絡與支持向量機的基礎
感知機學習旨在求出將訓練數據進行線性劃分的分離超平面。

感知機學習思路：
1.導入基于誤分類的損失函數
2.利用梯度下降法對損失函數進行極小化
3.代入參數得到感知機模型。

感知機學習算法分類：
原始形式、對偶形式。

感知機算法原始形式例題及詳解

例1 訓練數據集如圖所示，正實例點為 $x_1=(3,3)^{T}$ , $x_2=(4,3)^{T}$ ，負實例點為 $x_3=(1,1)^{T}$ ,試用感知機算法原始形式求感知機模型，令 $w=(w^{(1)},w^{(2)})^{T}$ , $x=(x^{(1)},x^{(2)})^{T}$

解答：

（1）建模最優化問題: $\underset{w,b}{min}L(w,b)= - \underset{x_i\in M}{\sum } y_i (w\cdot x_i+b )$

（2）取初值 $w_0=0,b_0=0$ ， $\eta =1$ ?

（3）按 $x_1,x_2,x_3$ 順序，對 $x_1=(3,3)^{T}$ , $y_1(w\cdot x1+b )= 0$ ，則 $x_1$ 為誤分類點。更新 $w,b$ ：

$w_1=w_0+y_1x_1=(3,3)^{T}$ , $b_1=b_0+\eta y_1=1$

得到線性模型： $w_1\cdot x+b_1=3x^{(1)}+3x^{(2)}+1=0$

（4）重新選取，對 $x_1,x_2$ ， $y_i(w_1\cdot x_i+b_1)>0$ ，則均為正確分類點，不更新 $w,b$ ；

對 $x_3=(1,1)^{T}$ ， $y_3(w_1\cdot x_3+b_1)< 0$ ，則 $x_3$ 為誤分類點，更新 $w,b$ ：

$w_2=w_1+y_3x_3=(2,2)^{T}$ , $b_2=b_1+\eta y_3=0$

得到線性模型： $w_2\cdot x+b_2=2x^{(1)}+2x^{(2)}=0$

（5）由此不斷迭代

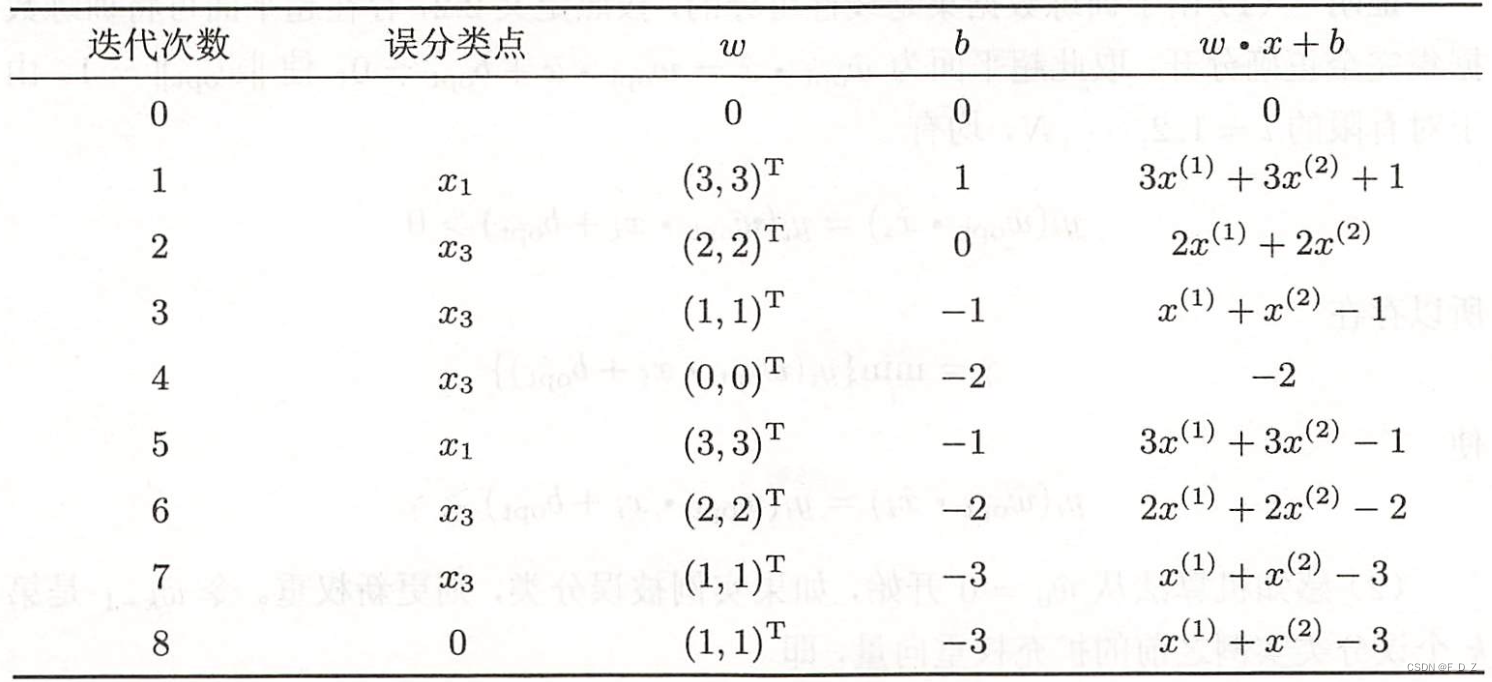
（6）直到 $w_7=(1,1)^{T}$ , $b_7=-3$

線性模型： $w_7\cdot x+b_7=x^{(1)}+x^{(2)}-3=0$

對所有數據點 $y_i(w_1\cdot x_i+b_1)>0$ ，則確定分離超平面： $x^{(1)}+x^{(2)}-3=0$

感知機模型 $f(x)=sign(x^{(1)}+x^{(2)}-3)$

分離超平面 $x^{(1)}+x^{(2)}-3=0$ 是按照 $x_1,x_3,x_3,x_3,x_1,x_3,x_3$ 的取點順序得到的
例1如果更換取點順序為 $x_1,x_3,x_3,x_3,x_2,x_3,x_3,x_3,x_1,x_3,x_3$ ，得到的分離超平面為：
$2x^{(1)}+x^{(2)}-5=0$
由此，可知結論：感知機算法采用不同的初值或選取不同的誤分類點順序，解可以不同

感知機算法對偶形式例題及詳解

例2?訓練數據集如圖所示，正實例點為 $x_1=(3,3)^{T}$ , $x_2=(4,3)^{T}$ ，負實例點為 $x_3=(1,1)^{T}$ ,試用感知機算法對偶形式求感知機模型，令 $w=(w^{(1)},w^{(2)})^{T}$ , $x=(x^{(1)},x^{(2)})^{T}$

解答：

（1）取 $\alpha_1=0,i=1,2,3,b=0,\eta =1$ ;

（2）計算Gram矩陣

$G=\begin{bmatrix} 18 & 21 &6 \\ 21& 25&7 \\ 6 & 7 & 2 \end{bmatrix}$

（3）誤分條件

$y_i (\sum_{j=1}^{N} \alpha _jy_jx_j\cdot x+ b)\leq 0$

（4）參數更新

$\alpha_i\leftarrow \alpha_i+1,b\leftarrow b+y_i$

（5）迭代

（6）最終得到

$w=\alpha_1x_1+\alpha_2x_2+\alpha_3x_3=2x_1+0x_2+5x_3=(1,1)^{T}$

$b=-3$

則，分離超平面： $x^{(1)}+x^{(2)}-3=0$

感知機模型： $f(x)=sign(x^{(1)}+x^{(2)}-3)$

與原始形式一致，感知機學習算法的對偶形式迭代收斂，且存在多個解

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/pingmian/92290.shtml
繁體地址，請注明出處：http://hk.pswp.cn/pingmian/92290.shtml
英文地址，請注明出處：http://en.pswp.cn/pingmian/92290.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！