大家好,接下來,我將帶來對于搜索篇的新內容,這部分我將打算圍繞DFS深度優先搜索去講解。
溫馨提示:由于這篇文章是接著上一篇文章的,如果新讀者沒有看過前一篇的話,推薦去看一下,不然有些地方可能會不懂。
接下來的每道題我相信大家都會有所收獲的!
1.題目概述:
這部分我將講解以下有關DFS的題目
1.選數 ---?P1036 [NOIP 2002 普及組] 選數 - 洛谷
2.飛機降落 ---?P9241 [藍橋杯 2023 省 B] 飛機降落 - 洛谷
3.八皇后 ---?P1219 [USACO1.5] 八皇后 Checker Challenge - 洛谷
4.數獨 ---?P1784 數獨 - 洛谷
這部分的題比上篇文章的題難度要提高挺多,大家可以如果有所困難可以多多思考一下。
2.選數

大家會發現,如果看了我前面的算法篇1的話其實很容易解決dfs遞歸的內容的。
但是大家會發現這里有一個新問題:如何求解一個數是不是素數呢?
這個的話有挺多的方法的,我在這里就用了一個簡單的方法
比如判斷一個數x是不是素數,由素數的定義我們可以知道:素數是大于1的正整數,而且只能被自己和1整除。
那么我們就可以從2開始到x所有的數拿去試除即可解決。
但是要判斷的這些數有點多了,我們就可以去選擇試除到根號x即可,具體的原因網上有證明,有興趣的讀者可以去看看。
(如果想判斷大量數字是否為素數,可以采用埃拉托色尼篩選法)
大家在看題目,發現結果并不會因為數字的順序不同而改變,所以是一種組合。
我們就得在dfs的參數中加入一個begin參數來表示從哪個數開始的
首先我們畫一下這個決策樹:
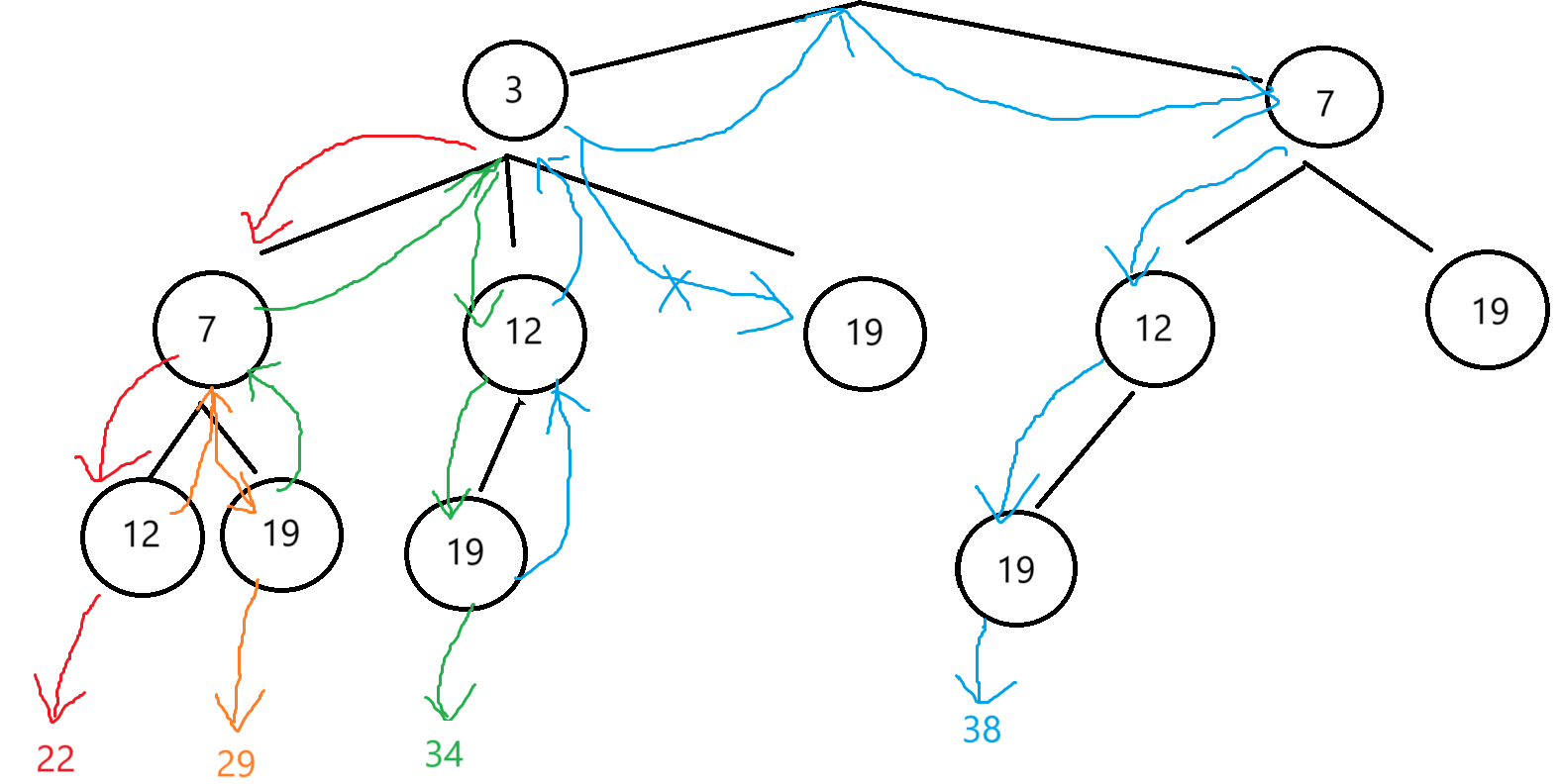
我們根據自己畫的決策樹就可以來寫代碼了:
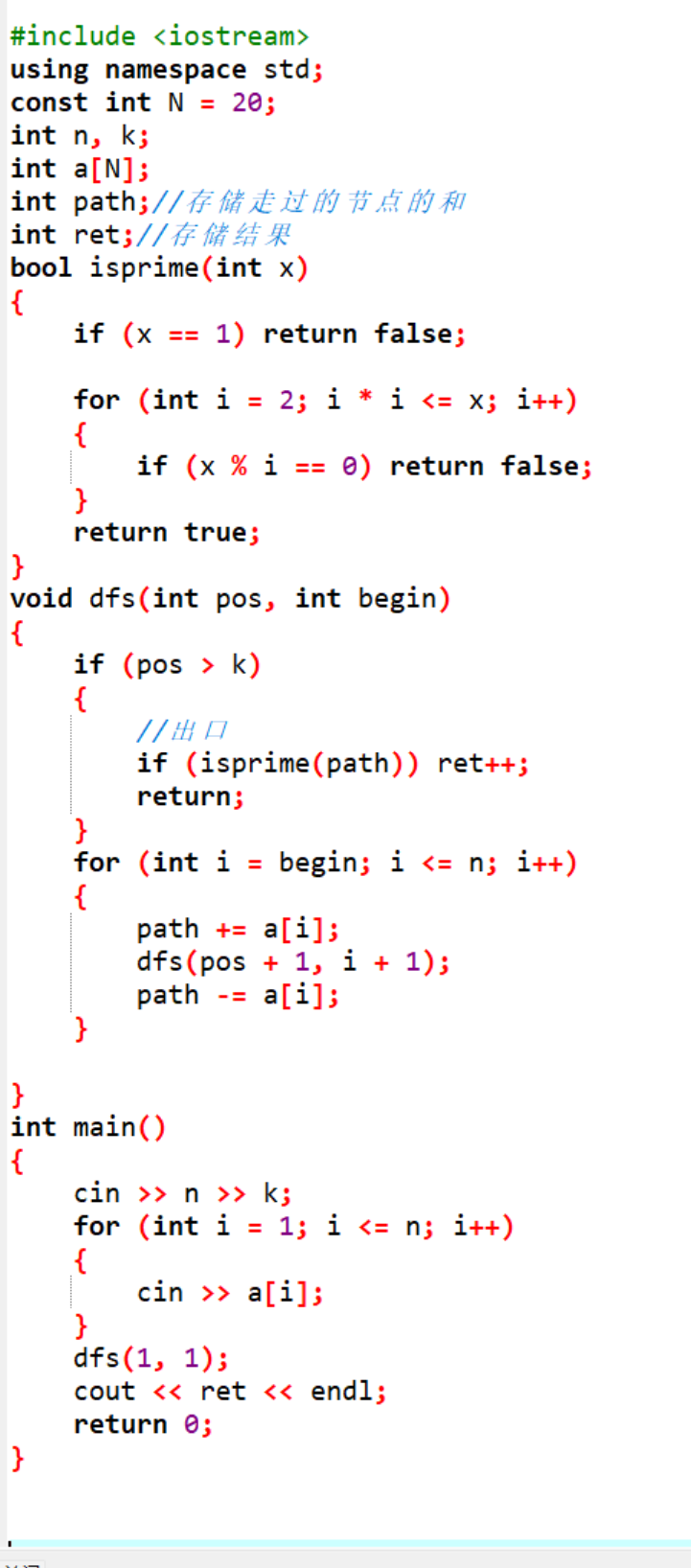
當然這道題跟上篇文章中的思路是一樣的,回溯遞歸
3.飛機降落
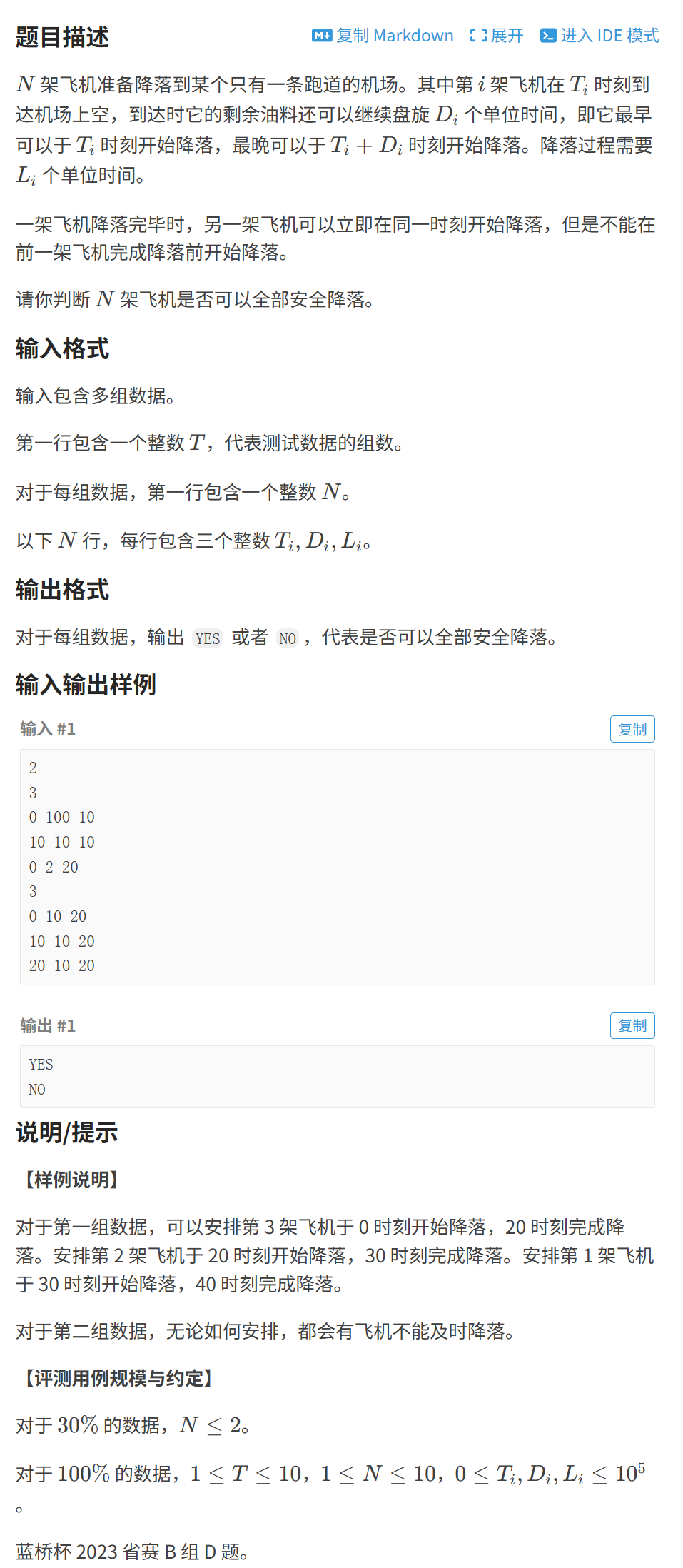
這道題的難度就比較高了,大家好好理解一下題目,可以嘗試做一做
那跟著博主的思路一起來看一下這道題吧。
這道題會發現的是如果直接來做的話,要安排好每架飛機的順序,保證該組飛機能夠安全降落,那么如果怎么都安排不出來,就代表這個不能及時降落了。所以如何安排順序就是我們的問題了,
我們這時候就可以通過搜索去枚舉出來所有情況。而且數據也是比較小的,通過搜索去做也不會出現超時,很顯然也在暗示我們去搜索。
由于這道題的枚舉類似排列,所以我們就不需要一個begin值去告訴該從什么位置遞歸了。
對于安排過的飛機,我們只需要通過一個bool st[]數組去標記一下即可。
當遇到了標記過的飛機就直接剪掉這個分支。
上一架飛機結束時間需要記錄一下,因為上一架飛機結束時間 ?>? 新飛機到達時間 + 最長盤旋時間,就代表了新飛機無法降落,我們也將這個分支給剪掉。
?那對于新飛機的結束時間怎么計算呢?
1.新飛機到達時間 >= 前一架飛機結束時間(新飛機到達的時間晚于前一架飛機的結束)
? ? ? ? 那么新飛機結束時間 = 新飛機的到達時間? ?+? ?新飛機的降落時間
2.新飛機到達時間 < 前一架飛機結束時間
? ? ? ? 比較一下
????????????????新飛機到達時間 + 盤旋時間? ?是否大于等于???前一架飛機結束時間
? ? ? ? 如果是 ---->? 新飛機能正常降落 ---- 新飛機結束時間 = 前一架飛機結束時間 + 新飛機降落時間
? ? ? ? 如果不是 ---> 新飛機無法正常降落
所以新飛機的結束時間? =? max(前飛機的結束時間, 新飛機到達時間) + 新飛機降落時間
根據博主的思路大家好好想想,將這個條件理解后,我們就可以來實現代碼了。
讀者可以先嘗試寫一下

這樣就可以實現出這到題了
大家可以仔細理解一下。
4.八皇后

大家還是可以先自己做一下,看看有哪里不懂的。
接下來就跟著博主的思路來理一下這道題吧,我們看完這道題后,我們知道的是什么呢?
我們無非就是要往這個矩陣中填棋子,將解的個數輸出即可。
我們對應的布局就如下面這樣
對應的246135數字都為對應的1,2,3,4,5,6行對應的列
所以我們有了對應的數字246135就可以得到對應的棋局布置了
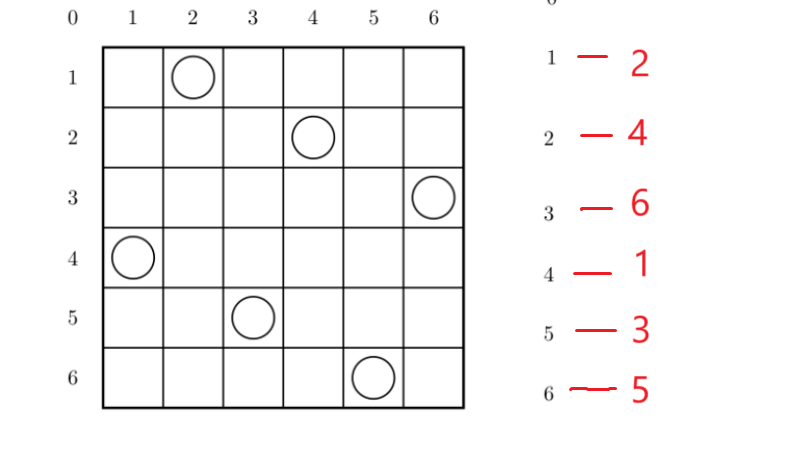
我們可以發現數據并不是很大,我們就可以去嘗試枚舉所有的情況了,將所有棋子的填充情況都枚舉一遍不就解決了嗎?
我們要填數肯定也有對應的限制了,那么限制是什么呢?
題目有說:行、列、對角線至多只能有一個棋子
所以我們通過這個條件就能夠減少我們枚舉的個數
我們簡單畫一下決策樹來:
這里并沒有畫完,大概理解一下,我們只要遍歷填充即可
大概邏輯還是dfs將結果存放起來
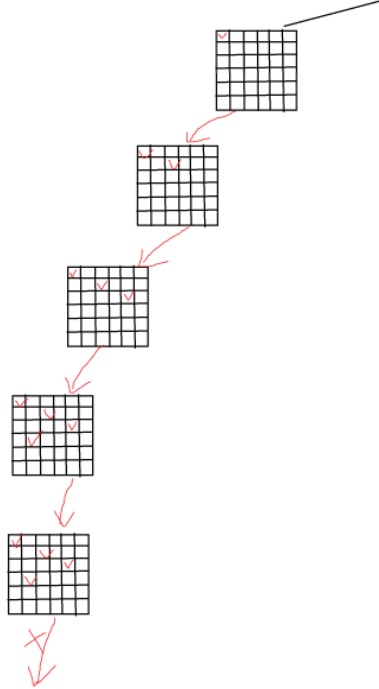
我們發現,其實要知道對應的行列有沒有放棋子很簡單的,由于放了1行,那么只能從2行開始放置了。所以我們只要用循環一行一行的放即可,我們再創建一個bool col[N]數組去標記哪些列被標記了。如果對應的列被放了就跳過它。
那么對角線如何解決呢?
我們可以使用一次函數來解決它。以向下的行數為x軸,向右的列為y軸,每個對角線都有自己的一個表達式:
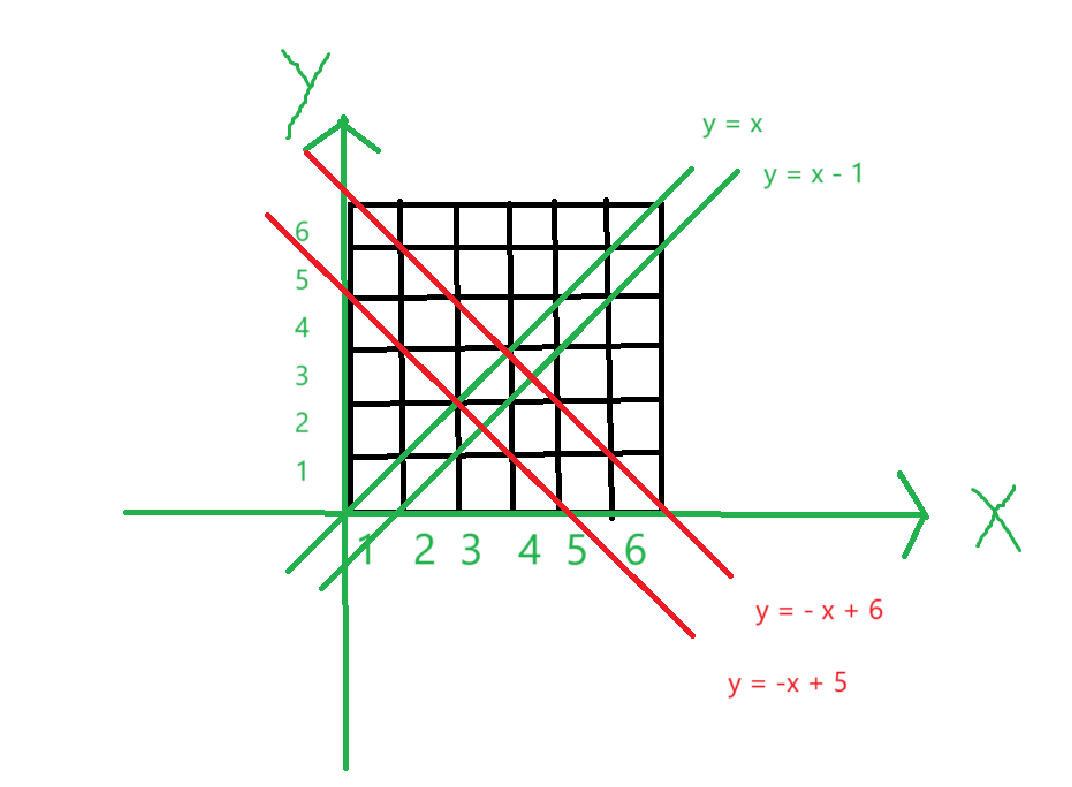
我們對于一個坐標位置就有兩條對角線:y - x = n? ? ?y + x = n
如果滿足y - x = n或者y + x = n就代表對應的對角線已經有了棋子了!
我們只要將填過棋子的 y - x 和 y + x得到的值放在對應的數組就可以標記對角線了
但是有可能y - x會出現負數?怎么解決呢?
我們只要給y - x加上一個n值(偏移量)即可
現在bool? st[2 * N];就可以標記對角線了,而且由于每個節點會出現兩條對角線,所以要空間要開辟2 * N的大小!
我們需要統計前幾個結果的路徑所以還得用vector<int> path去標記成功的結果。
現在我們就來寫一下代碼吧:
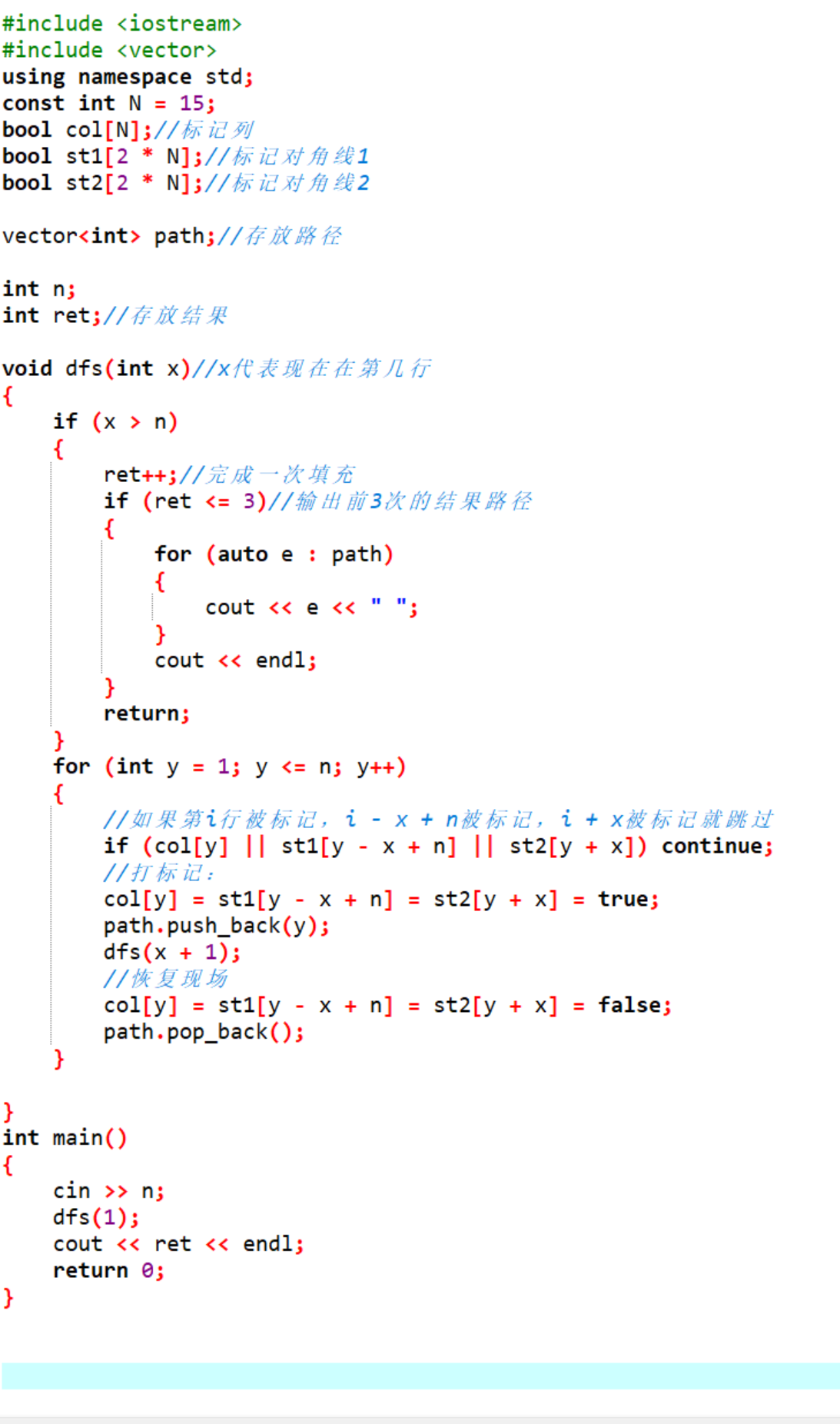
大家可以好好理解一下這段代碼,再和博主我的思路畫圖結合一起來分析。
大家理解了其中的主要思維,就能夠自己寫出來了
5.數獨
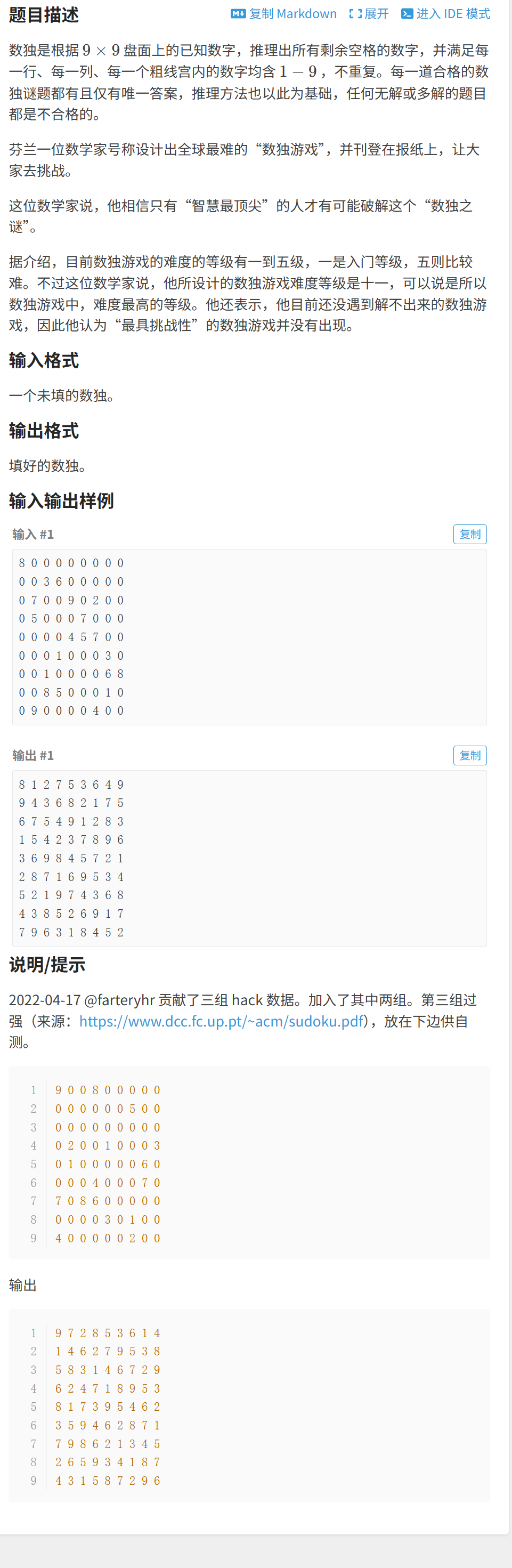
這道題題目講的很簡單給出一個未知的數獨,然后讓我們把它填完,再輸出即可。
大家還是一樣可以先自己思考一下該如何解決!
下面跟著博主的思路來看看這道題吧:
首先我們會接收到一個二維數組,這里面會有很多0,這些0就是我們需要去填充的部分。
?對于每個0我們都可以在1---9的數字去填充
但是會因為其他已經有了數字的位置導致有些數不能填。
玩過數獨的都知道,我們每行都是要在1-9去填充,3 * 3的格子內也得要在1--9
對于對應的行列,我們可以使用一個二維數組去標記第幾行的哪幾個數被填過,第幾列的哪些數被填過。
bool row[N][N]? ----------? ?row[i][x]表示第x行的i數被填充過
bool col[N][N]? ?----------? ?col[i][y]表示第y列的i數被填充過
那么對于這個3 * 3的格子怎么解決呢?
我們看看下面的圖:
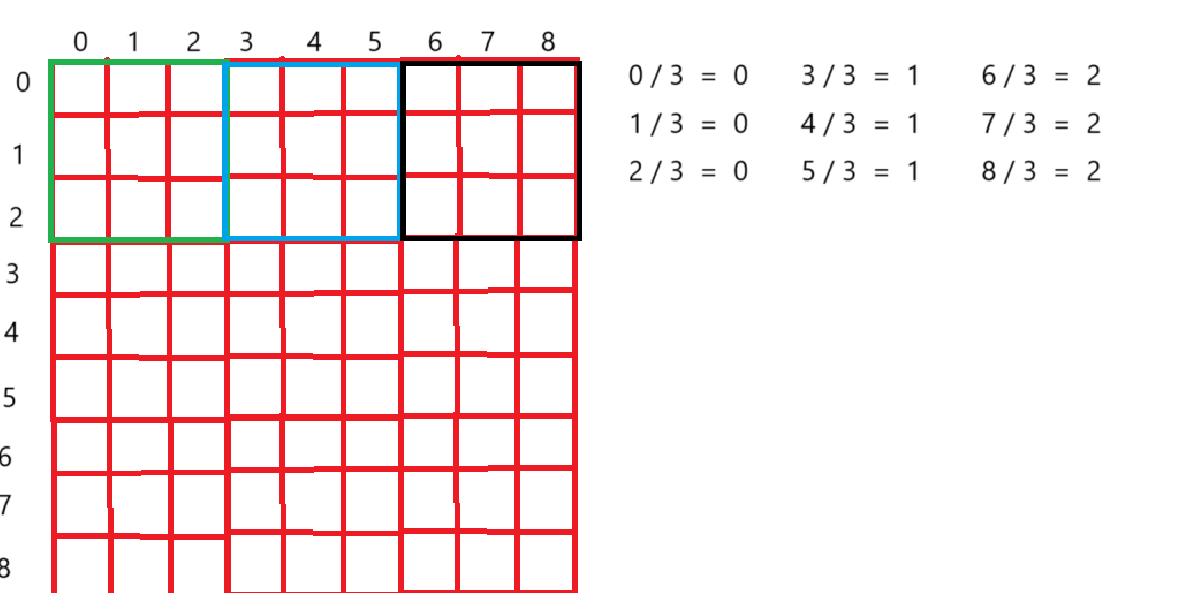
我們只要下標從 0 --- 8來標記數組,就可以通過對應的下標除以3就可以得到是第幾個3 * 3的小格子
對應的這9 * 9的數獨就有9個3 * 3的格子,就可以用對應點的x, y通過x / 3 , y / 3去找到對應的3 * 3格子
我們創建一個三維數組st來標記即可解決了
bool st[N][N][N]? ?-----? ?st[x / 3][y / 3][i] ---- 就代表第x / 3,行y / 3列的3 * 3格子中填充了數i
現在我們最困難的地方已經解決,現在就是寫代碼的階段,讀者可以跟著思路自己去寫一下!
代碼如下:
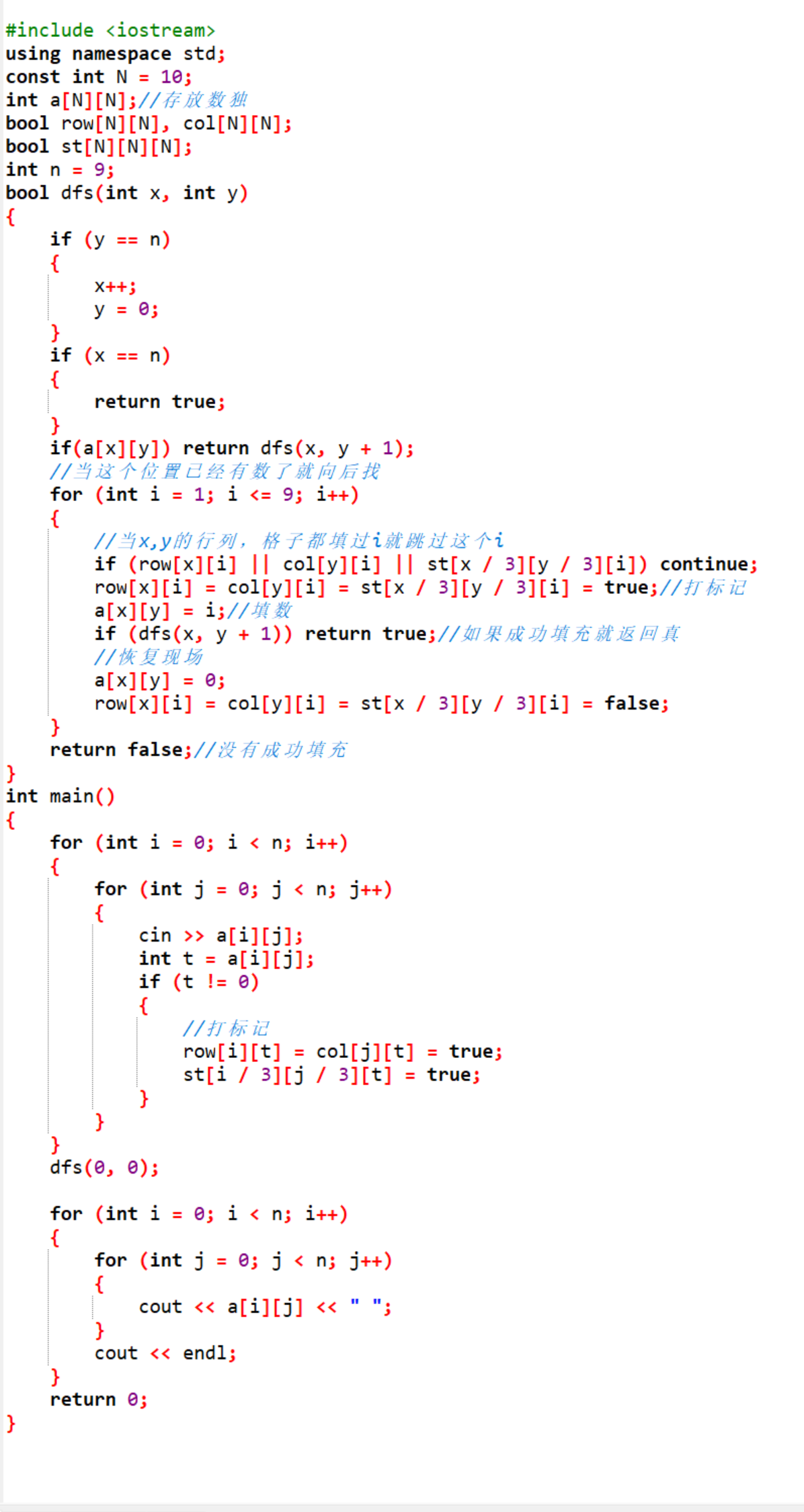
這道題中dfs里面還多出來了個判斷y和x的合法性的判斷,這個地方需要特別注意一下。
6.結語
很高興大家能夠看到這里,這一部分的題難度有所提高,大家要好好思考思考。
好好理解其中的思考過程,相信大家會有所收獲的。
后面我會持續更新,大家多多點贊收藏+關注。






鼠標控制、可拓展陀螺儀與腳本控制)
)
)

)

)


)
——梯度處理、邊緣檢測、圖像輪廓)

 用戶管理命令)
