（9）NMPC非線性模型預測控制及機械臂ROS控制器實現

前言

本篇介紹Nonlinear Model Predictive Control，非線性模型預測控制，MPC是一種現代先進的控制方法，而NMPC特指對非線性模型的控制，其核心思想是在每個控制周期內利用系統的非線性模型及損失函數，預測未來一段時間內的系統行為，通過求解有限時域內的最優控制問題，實時生成最優控制輸入。NMPC能夠處理復雜約束和多變量系統，目前在無人機、自動駕駛領域廣泛使用，隨著目前硬件算力的提升，逐步地在機器人上也開始逐漸有所應用。

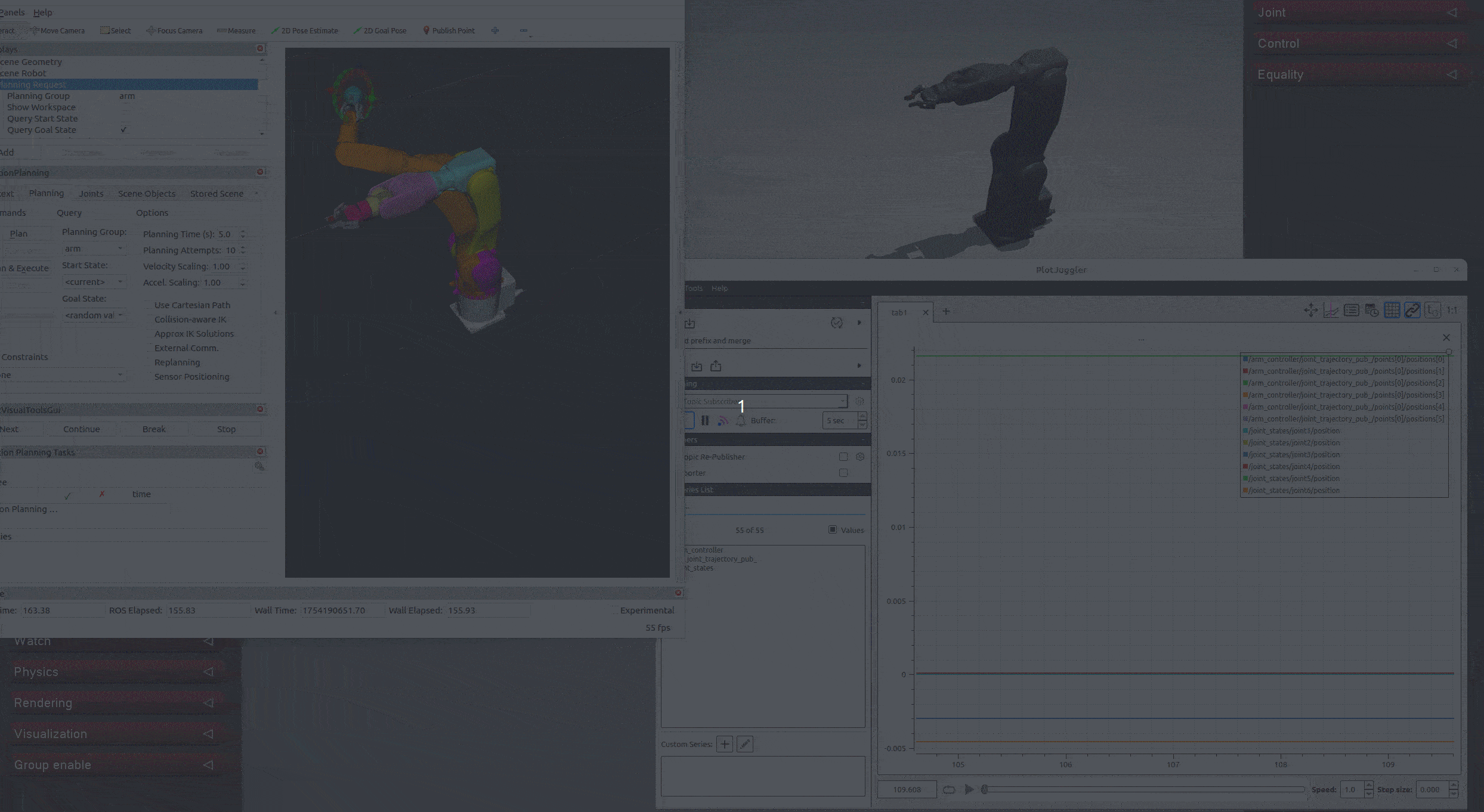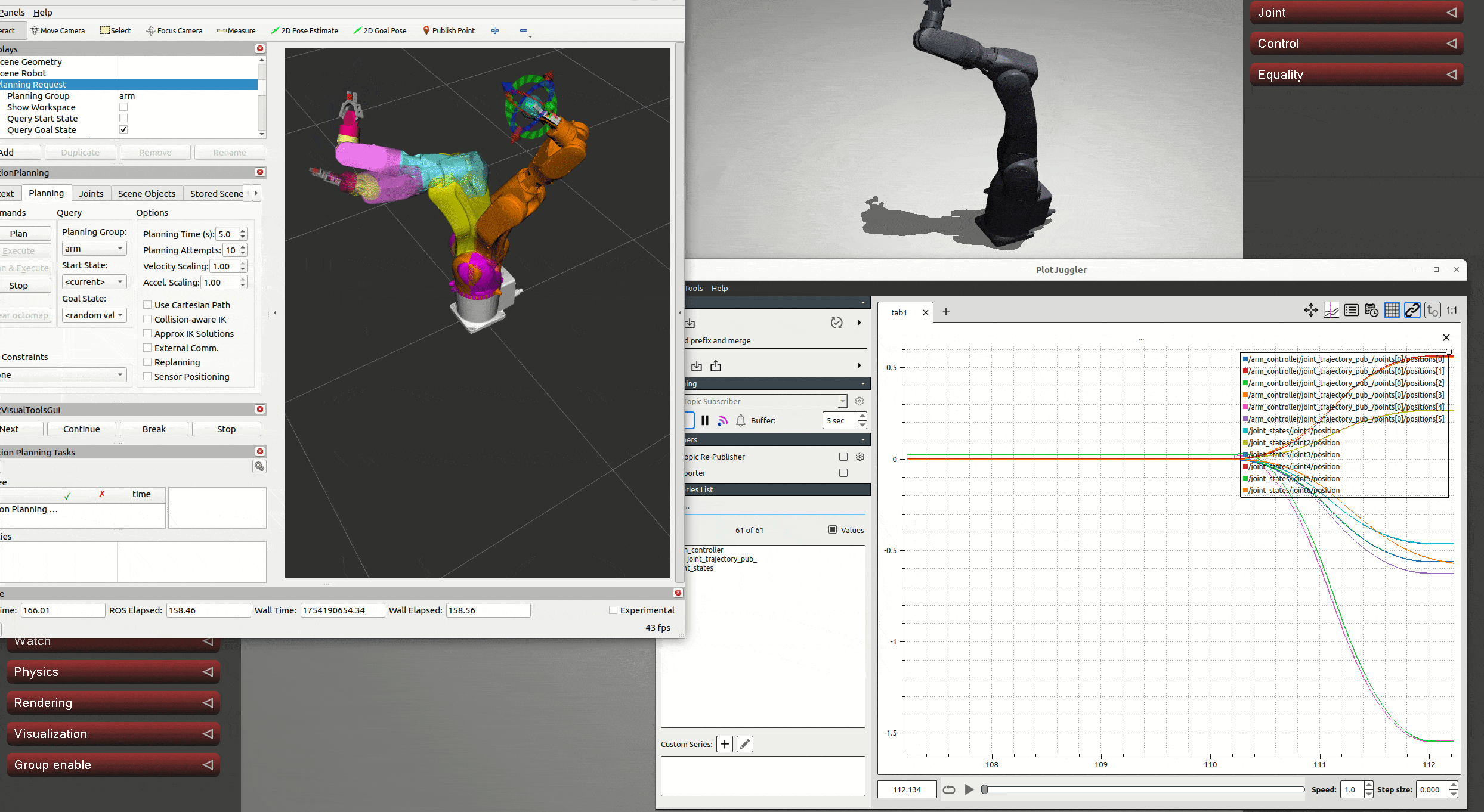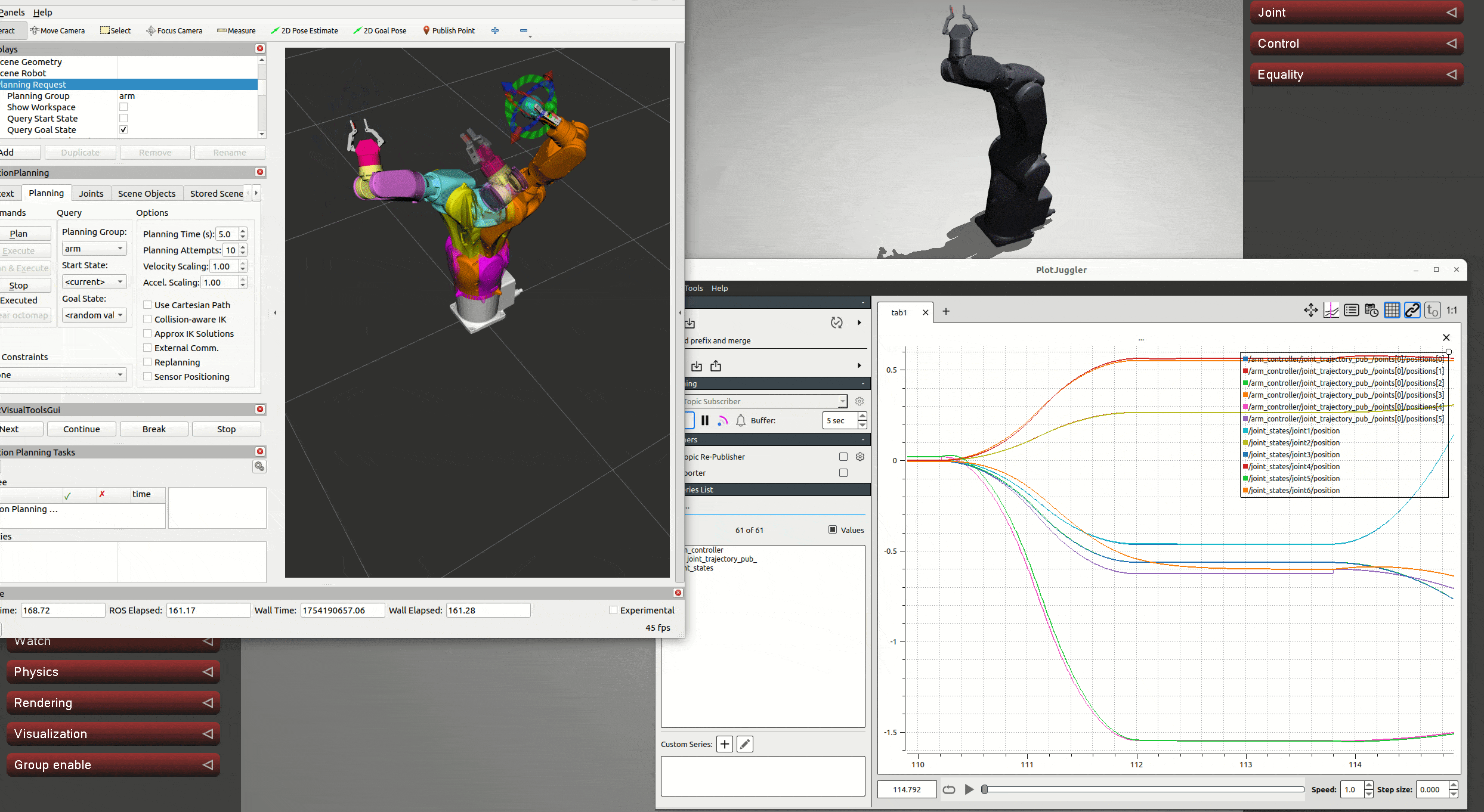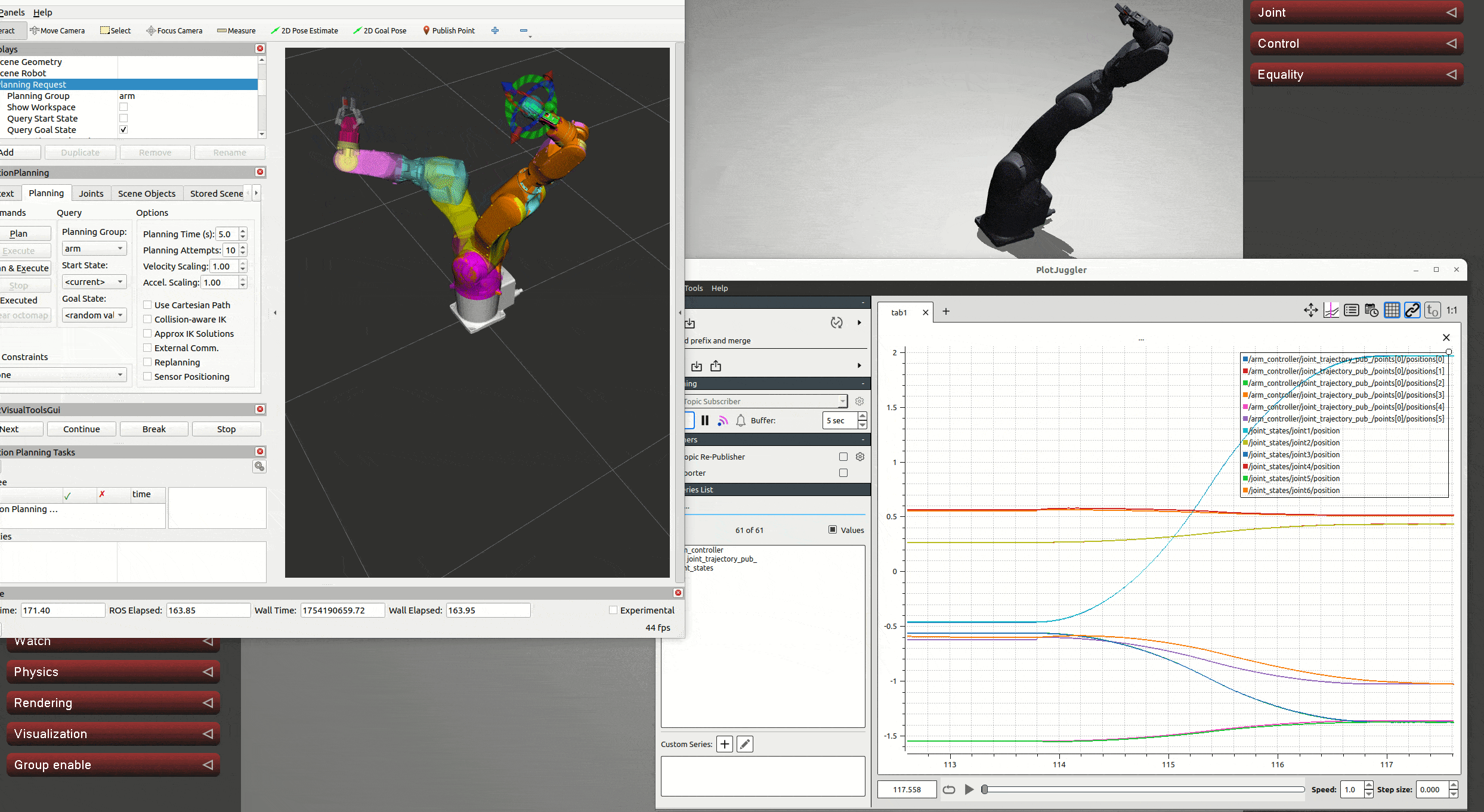
可以發現其強大之處不僅在于精準度，還有極快的響應速度，且多次測試后發現其不像先前介紹的幾種控制器那樣在極端狀態下會失穩亂轉，最多是在固定位置抖動。

1. NMPC介紹

1.1 最優控制

最優控制研究如下問題（離散形式）：

$\min_{\{u_k\}_{k=0}^{N-1},\{x_k\}_{k=0}^{N}} J = \sum_{k=0}^{N-1} L(x_k, u_k, k) + \Phi(x_N) \\ s.t. \quad \quad \quad \quad \quad x_{k+1} = f(x_k, u_k), \\ . \quad \quad \quad \quad \quad \quad \quad x_0 = x_{\text{init}} \\ . \quad \quad \quad \quad \quad \quad \quad x_{min}\leq x_k \leq x_{max} \\ . \quad \quad \quad \quad \quad \quad \quad u_{min}\leq u_k \leq u_{max}$

即找到最優控制策略，使得在滿足約束：系統動態方程、初始條件、狀態約束、控制約束及其他約束的情況下，找到最優的控制策略u及狀態軌跡x（0->N），使得cost function J值最小。這與RL的思路師出同門，RL在于找到最大獎勵，而最優控制在于找到最小損失。

對于上述問題的求解，有一系列的數值優化方法，尤其對于convex問題甚至存在解析解，這部分內容很多，希望詳細了解可以參考課程【最優控制 16-745 2024】卡耐基梅隆—中英字幕_嗶哩嗶哩_bilibili

1.2 貝爾曼最優性理論

Bellman Principle指的是從當前狀態出發的最優策略，其任何一個未來時刻的剩余策略也一定是從那一時刻出發的全局最優策略。

大意就是，如果我知道從A到E，走A->C->E->B->D最近，那么從C出發，也一定是走C->E->B->D最近，否則如果變成了C->B->E->D最近的話，那么A到E的路徑就應該是A->C->B->E->D，與前提矛盾。

這意味著不論取全局最優軌跡其中的任意一段軌跡，這段軌跡也是局部最優的。

1.3?NMPC

對于1.1提到的最優控制問題，其存在兩個問題：

1. 直接生成整條軌跡時，沒有反饋機制（用Riccati遞歸除外），魯棒性、穩定性差

2. 直接計算0->N，求解計算量大，無法用于實時控制

所以MPC是一種“退而求其次”的思想，想象整條軌跡N，直接求解最優問題得到的全局最優軌跡，而MPC的思想是每輪控制循環只取未來的N_norizon個軌跡點，一般是10-20個，求解如下問題：

$\min_{\{u_k\}_{k=0}^{N_{horizon}-1},\{x_k\}_{k=0}^{N_{horizon}}} J = \sum_{k=0}^{N-1} L(x_k, u_k, k) + \Phi(x_{N_{horizon}}) \\ s.t. \quad \quad \quad \quad \quad x_{k+1} = f(x_k, u_k), \\ . \quad \quad \quad \quad \quad \quad \quad x_0 = x_{\text{init}} \\ . \quad \quad \quad \quad \quad \quad \quad x_{min}\leq x_k \leq x_{max} \\ . \quad \quad \quad \quad \quad \quad \quad u_{min}\leq u_k \leq u_{max}$

之后每輪循環，只執行優化所得的第一個控制向量u0，根據貝爾曼最優性原理，u0一定是當前狀態下的最優策略。而因為MPC是不斷取局部N_norizon個軌跡點，其生成的最終控制策略是局部最優，而非全局最優。

而非線性MPC與線性MPC的最大區別在于，系統的動態方程 $x_{k+1} = f(x_k, u_k)$ 無法線性化表達為 $x_{k+1} =Ax_k+Bu_k$ （如果可以的話，由于cost function J一般取為二次型，其最優問題求解問題變為convex QP，存在解析解，求解過程極簡）（雖然也可以通過局部一階泰勒展開，但是對于強非線性系統，精準度很差），求解難度更高。

1.4?機械臂的NMPC形式

取 $x = \begin{Bmatrix} q\\ \dot{q} \end{Bmatrix}$ ，之后取

$\min_{\{u_k\}_{k=0}^{N_{horizon}-1},\{x_k\}_{k=0}^{N_{horizon}}} J = \sum_{k=0}^{N-1} x_k^TQx_k + u_k^TRu_k +x_{N_{horizon}}^TQ_fx_{N_{horizon}} \\\\ s.t. \quad \quad \quad \quad \quad x_{k+1} = f(x_k, u_k), \\ . \quad \quad \quad \quad \quad \quad \quad x_0 = x_{\text{init}} \\ . \quad \quad \quad \quad \quad \quad \quad x_{min}\leq x_k \leq x_{max} \\ . \quad \quad \quad \quad \quad \quad \quad u_{min}\leq u_k \leq u_{max}$

$x_{k+1} = f(x_k, u_k)$ 可以用歐拉法或RK4對機械臂的狀態空間方程離散得到，后文ROS控制器實現時介紹。

2. ROS控制器實現

相對于前幾篇介紹過的控制方法，在ROS控制器中實現NMPC過程非常復雜，實際上跟ros controller關系都不大了，基本上全程在調用外部函數，下面盡可能詳細介紹。

2.1 使用pinocchio&casadi導出機械臂動態方程

在C++中用pinocchio讀取機械臂urdf，用pinocchio::casadi::sym定義q、q_dot、tau為變量，調用pinocchio::crba和pinocchio::nonLinearEffects拼出標準動態方程，之后用casadi導出動態方程（連續形式），詳見：

#include <pinocchio/parsers/urdf.hpp>
#include <pinocchio/multibody/model.hpp>
#include <pinocchio/algorithm/rnea.hpp>
#include <pinocchio/algorithm/crba.hpp>
#include <pinocchio/autodiff/casadi.hpp>
#include <casadi/casadi.hpp>
#include <Eigen/Dense>
#include <iostream>// 工具函數：Eigen::Matrix<SX, -1, 1> 轉 std::vector<SX>
template <typename Derived>
std::vector<casadi::SX> eigen_to_stdvector(const Eigen::MatrixBase<Derived>& m) {std::vector<casadi::SX> v(m.size());for (int i = 0; i < m.size(); ++i)v[i] = m(i);return v;
}template <typename Derived>
std::vector<std::vector<casadi::SX>> eigenmat_to_stdvectorvec(const Eigen::MatrixBase<Derived>& m) {std::vector<std::vector<casadi::SX>> v(m.rows());for (int i = 0; i < m.rows(); ++i) {v[i].resize(m.cols());for (int j = 0; j < m.cols(); ++j)v[i][j] = m(i, j);}return v;
}int main() {std::string urdf_path = "/home/mr/myproject/src/my_mujoco_test/urdf/my_mujoco_arm_adaptive.urdf";pinocchio::Model model;pinocchio::urdf::buildModel(urdf_path, model);using SX = casadi::SX;using VectorXsx = Eigen::Matrix<SX, Eigen::Dynamic, 1>;using MatrixXsx = Eigen::Matrix<SX, Eigen::Dynamic, Eigen::Dynamic>;VectorXsx q(model.nq), v(model.nv), tau(model.nv);pinocchio::casadi::sym(q, "q");pinocchio::casadi::sym(v, "v");pinocchio::casadi::sym(tau, "tau");auto model_sx = model.cast<SX>();pinocchio::DataTpl<SX> data_sx(model_sx);MatrixXsx M = pinocchio::crba(model_sx, data_sx, q);VectorXsx nle = pinocchio::nonLinearEffects(model_sx, data_sx, q, v);// 用CasADi的solvecasadi::SX M_casadi = casadi::SX::zeros(M.rows(), M.cols());for (int i = 0; i < M.rows(); ++i)for (int j = 0; j < M.cols(); ++j)M_casadi(i, j) = M(i, j);casadi::SX tau_minus_nle = casadi::SX::vertcat(eigen_to_stdvector(tau - nle));casadi::SX vdot_casadi = casadi::SX::solve(M_casadi, tau_minus_nle);// 拼接x, xdotcasadi::SX x_casadi = casadi::SX::vertcat(eigen_to_stdvector(q));x_casadi = casadi::SX::vertcat({x_casadi, casadi::SX::vertcat(eigen_to_stdvector(v))});casadi::SX xdot_casadi = casadi::SX::vertcat(eigen_to_stdvector(v));xdot_casadi = casadi::SX::vertcat({xdot_casadi, vdot_casadi});casadi::SX u_casadi = casadi::SX::vertcat(eigen_to_stdvector(tau));casadi::Function f_dyn("f_dyn", {x_casadi, u_casadi}, {xdot_casadi}, {"x", "u"}, {"xdot"});f_dyn.save("robot_dynamics.casadi");std::cout << "Saved CasADi function robot_dynamics.casadi" << std::endl;return 0;
}

運行后會生成一個插件，根據命名比如是 my_robot_dynamics，在終端運行這個插件（./my_robot_dynamics）會在運行目錄生成robot_dynamics.casadi。

2.2?使用acados定制NLP求解器

如下，用python使用acados生成NLP求解器，包裝為C++程序供ROS控制器使用。

讀取剛剛生成的robot_dynamics.casadi，定義N_horizon、Tf、狀態權重Q、輸入權重R、終端狀態權重Q_f，注意以下幾點：

1. N_horizon一般取10-20，根據計算性能取，數字越大預測全局性越好，但求解耗時越長

2. Tf為預測長度的總時長，比如我取N_horizon=10，Tf=0.1，相當于每輪求解預測未來0.1s，采樣頻率100Hz，這個頻率要小于等于ros控制器的循環頻率，否則會出現“跳點”導致劇烈抖動

3. 一般取R比Q小一些，Q/R的比值越大響應速度越快，但過大可能出現抖動，反之則越柔順，但響應速度會受到影響

4. 一般取Qf為Q的5-10倍

5.?acados定義求解器時，N_horizon、Tf作為結構參數是不支持對外暴露接口的，即不能在調用函數時通過外部傳參更改，一旦生成就定死了。所以即使Q、R、Qf、狀態/輸入約束可以，我也干脆都寫死了，每次調試重新運行程序生成C++程序就好了。

6. 離散方法選擇“ERK”，RK4方法，離散精度較高

import casadi as ca
import numpy as np
from acados_template import AcadosOcp, AcadosOcpSolver, AcadosModelf_dyn = ca.Function.load("robot_dynamics.casadi")
nq, nv = 6, 6model = AcadosModel()
model.x = ca.MX.sym('x', nq + nv)
model.u = ca.MX.sym('u', nv)
model.f_expl_expr = f_dyn(model.x, model.u)
model.name = "robot_nmpc"ocp = AcadosOcp()
ocp.model = model
N_horizon = 10
Tf = 0.1
ocp.dims.N = N_horizon
ocp.solver_options.tf = Tf
# 輸入約束
u_min = -100 * np.ones(nv)
u_max =  100 * np.ones(nv)
u_min[3] = -40
u_min[4] = -40
u_min[5] = -40
u_max[3] = 40
u_max[4] = 40
u_max[5] = 40
ocp.constraints.lbu = u_min
ocp.constraints.ubu = u_max
ocp.constraints.idxbu = np.arange(nv)
# 狀態約束
idxbx = np.array([6,7,8])              # 約束前6個分量（關節位置）
lbx = np.array([-3.0, -3.0, -3.0])  # 下界
ubx = np.array([ 3.0,  3.0,  3.0])  # 上界
ocp.constraints.idxbx = idxbx
ocp.constraints.lbx = lbx
ocp.constraints.ubx = ubxQ = 200 * np.eye(nq + nv)
for i in range(nv):Q[i + nq, i + nq] = 10  # 只對速度項施加較小的權重
Q[3,3] = 100
Q[4,4] = 100
Q[5,5] = 100
Q[9,9] = 5
Q[10,10] = 5
Q[11,11] = 5
R = 250 * np.eye(nv)
R[3,3] = 50
R[4,4] = 50
R[5,5] = 50
Q_terminal = Q * 10  
ocp.cost.cost_type = 'LINEAR_LS'
ocp.cost.cost_type_e = 'LINEAR_LS'
ocp.cost.W = Q
ocp.cost.W_e = Q_terminal
ocp.cost.Vx = np.eye(nq + nv)
ocp.cost.Vu = np.zeros((nq + nv, nv))
ocp.cost.Vx_e = np.eye(nq + nv)
ocp.cost.yref = np.zeros(nq + nv)
ocp.cost.yref_e = np.zeros(nq + nv)
ocp.solver_options.qp_solver = 'FULL_CONDENSING_QPOASES'
ocp.solver_options.integrator_type = 'ERK'  # 使用RK4方法離散動態方程
ocp.solver_options.nlp_solver_type = 'SQP_RTI'
ocp.solver_options.hessian_approx = 'GAUSS_NEWTON'
# ocp.solver_options.nlp_tol = 1e-6         # NLP全局容差
# ocp.solver_options.nlp_tol_eq = 1e-6      # 等式約束容差
# ocp.solver_options.nlp_tol_ineq = 1e-6    # 不等式約束容差
# ocp.solver_options.qp_tol = 1e-8          # QP子問題容差
# 先占位（必須有，哪怕初值不重要）
ocp.constraints.x0 = np.zeros(nq + nv)solver = AcadosOcpSolver(ocp, json_file="acados_ocp.json")def nlmpc_acados_step(x0, x_ref_traj):solver.reset()solver.set(0, "x", x0)for i in range(N_horizon):solver.set(i, "yref", x_ref_traj[i])solver.set(N_horizon, "yref", x_ref_traj[-1])   status = solver.solve()if status != 0:print(f"acados solve failed: {status}")u0 = solver.get(0, "u")return u0if __name__ == "__main__":x0 = np.zeros(nq + nv)x_ref_traj = np.tile(np.concatenate([np.ones(nq), np.zeros(nv)]), (N_horizon+1, 1))u0 = nlmpc_acados_step(x0, x_ref_traj)print("MPC optimal u0:", u0)

運行以上程序，將會生成如下一系列文件

之后才cmakelist.txt中將生成的程序都導入到環境中

add_library(${PROJECT_NAME}SHAREDcontroller/my_mpc_controller.cppcontroller/c_generated_code/acados_solver_robot_nmpc.ccontroller/c_generated_code/acados_sim_solver_robot_nmpc.ccontroller/c_generated_code/robot_nmpc_model/robot_nmpc_expl_ode_fun.ccontroller/c_generated_code/robot_nmpc_model/robot_nmpc_expl_vde_forw.ccontroller/c_generated_code/robot_nmpc_model/robot_nmpc_expl_vde_adj.c
)

2.3 ROS2控制器調用NLP求解器

在頭文件中增加定義：

int N_mpc_;
double Tf_;
std::vector<Eigen::VectorXd> X_ref_window_;
robot_nmpc_solver_capsule *acados_ocp_capsule_;
trajectory_msgs::msg::JointTrajectoryPoint interp_pt_;
bool dummy_reached_;
double t_query_sec_;
rclcpp::Duration t_query_{rclcpp::Duration::from_seconds(0.0)};

在控制器onit部分對上述變量進行初始化，其中robot_nmpc_solver_capsule *acados_ocp_capsule_;就是我們剛剛生成的求解器對象的指針。

雖然在這里定義的N_mpc和Tf不能改變NLP求解器中的值，但是后續要供其他變量使用，所以提前定義好。

在on_active處創建求解器

acados_ocp_capsule_ = robot_nmpc_acados_create_capsule();
if (robot_nmpc_acados_create(acados_ocp_capsule_) != 0) {RCLCPP_ERROR(get_node()->get_logger(), "Failed to create acados solver");return controller_interface::CallbackReturn::ERROR;
}

在update中調用，關鍵在于如下這些NLP求解器的初始化過程，其參數命名等都是固定的，只需要把X_window_ref_（每輪mpc計算的參考軌跡段）和xic_（每輪mpc求解的初始位置，即當前位置）填入即可。

        ocp_nlp_in *nlp_in = robot_nmpc_acados_get_nlp_in(acados_ocp_capsule_);ocp_nlp_out *nlp_out = robot_nmpc_acados_get_nlp_out(acados_ocp_capsule_);ocp_nlp_config *nlp_config = robot_nmpc_acados_get_nlp_config(acados_ocp_capsule_);ocp_nlp_dims *nlp_dims = robot_nmpc_acados_get_nlp_dims(acados_ocp_capsule_);// 初始約束ocp_nlp_constraints_model_set(nlp_config, nlp_dims, nlp_in, nlp_out, 0, "lbx", xic.data());ocp_nlp_constraints_model_set(nlp_config, nlp_dims, nlp_in, nlp_out, 0, "ubx", xic.data());// 設置 yref (軌跡參考)for (int i = 0; i < X_ref_window_.size()-1; ++i) {ocp_nlp_cost_model_set(nlp_config, nlp_dims, nlp_in, i, "yref", X_ref_window_[i].data());}// 終端參考ocp_nlp_cost_model_set(nlp_config, nlp_dims, nlp_in, X_ref_window_.size(), "yref", X_ref_window_.back().data());int status = robot_nmpc_acados_solve(acados_ocp_capsule_);if (status != 0) {RCLCPP_WARN(get_node()->get_logger(), "acados solve failed: %d", status);}std::vector<double> u0(joint_names_.size());ocp_nlp_out_get(nlp_config, nlp_dims, nlp_out, 0, "u", u0.data());

詳見具體程序：?

    //update函數在控制器被激活后每次更新時調用，主要用于處理實時數據和執行控制邏輯，屬于主函數controller_interface::return_type MyMpcController::update(const rclcpp::Time & time, const rclcpp::Duration & period){   dt_ = period.seconds() + (period.nanoseconds() * 1e-9); // 計算時間間隔，單位為秒double effort_command = 0.0; // 初始化關節力矩命令Eigen::VectorXd zeros = Eigen::VectorXd::Zero(joint_names_.size());Eigen::VectorXd double_zeros = Eigen::VectorXd::Zero(joint_names_.size() * 2);bool reached_end = false;// 獲取 acados 內部結構體ocp_nlp_in *nlp_in = robot_nmpc_acados_get_nlp_in(acados_ocp_capsule_);ocp_nlp_out *nlp_out = robot_nmpc_acados_get_nlp_out(acados_ocp_capsule_);ocp_nlp_config *nlp_config = robot_nmpc_acados_get_nlp_config(acados_ocp_capsule_);ocp_nlp_dims *nlp_dims = robot_nmpc_acados_get_nlp_dims(acados_ocp_capsule_);if (new_msg_){trajectory_msg_ = *traj_msg_external_point_ptr_.readFromRT(); // 從實時緩沖區讀取完整的軌跡信息start_time_ = time; // 記錄控制器開始時間new_msg_ = false; // 重置新消息標志位}for (size_t i = 0; i < joint_effort_command_interfaces_.size(); ++i) {last_torques_[i] = joint_effort_command_interfaces_[i].get().get_value(); // 保存上一次的關節力矩}if (trajectory_msg_ != nullptr) // 如果軌跡不為空{   // 到位檢查double cur_time_sec = (time - start_time_).seconds();double total_time = trajectory_msg_->points.back().time_from_start.sec +trajectory_msg_->points.back().time_from_start.nanosec * 1E-9;if (cur_time_sec >= total_time){reached_end = true; // 如果當前插值點位置等于軌跡最后一個點的位置，則認為到達末尾}if (!reached_end) {double dt_mpc = Tf_ / double(N_mpc_);X_ref_window_.clear();for (size_t k = 0; k < N_mpc_; ++k) {t_query_sec_ = (time - start_time_).seconds() + k * dt_mpc;t_query_ = rclcpp::Duration::from_seconds(t_query_sec_);interpolate_trajectory_point(*trajectory_msg_, t_query_, interp_pt_, dummy_reached_);Eigen::VectorXd x_ref(joint_names_.size() * 2);for (size_t j = 0; j < joint_names_.size(); ++j) {x_ref(j) = interp_pt_.positions[j];x_ref(j + joint_names_.size()) = (interp_pt_.velocities.size() > j) ? interp_pt_.velocities[j] : 0.0;}X_ref_window_.push_back(x_ref);if (k == 0) {point_interp_ = interp_pt_; // 更新當前插值點}}} else {// 如果軌跡執行到達末尾卻沒有到達目標位置，使用最后一個點的值填充參考軌跡point_interp_ = trajectory_msg_->points.back();X_ref_window_.clear();// 沒有新目標，保持當前位置for (size_t i = 0; i < joint_names_.size(); ++i) {X_ref_[i] = point_interp_.positions[i]; // 獲取期望關節位置X_ref_[i + joint_names_.size()] = 0.0; // 獲取期望關節速度}X_ref_window_.clear();for (size_t k = 0; k < N_mpc_; ++k) {X_ref_window_.push_back(X_ref_);}}// 調用MPC控制算法，計算關節力矩命令Eigen::VectorXd xic = Eigen::VectorXd::Zero(joint_names_.size() * 2);for (size_t i = 0; i < joint_names_.size(); ++i) {xic[i] = joint_position_state_interfaces_[i].get().get_value(); // 獲取當前關節位置xic[i + joint_names_.size()] = joint_velocity_state_interfaces_[i].get().get_value(); // 獲取當前關節速度}// 初始約束ocp_nlp_constraints_model_set(nlp_config, nlp_dims, nlp_in, nlp_out, 0, "lbx", xic.data());ocp_nlp_constraints_model_set(nlp_config, nlp_dims, nlp_in, nlp_out, 0, "ubx", xic.data());// 設置 yref (軌跡參考)for (int i = 0; i < X_ref_window_.size()-1; ++i) {ocp_nlp_cost_model_set(nlp_config, nlp_dims, nlp_in, i, "yref", X_ref_window_[i].data());}// 終端參考ocp_nlp_cost_model_set(nlp_config, nlp_dims, nlp_in, X_ref_window_.size(), "yref", X_ref_window_.back().data());int status = robot_nmpc_acados_solve(acados_ocp_capsule_);if (status != 0) {RCLCPP_WARN(get_node()->get_logger(), "acados solve failed: %d", status);}std::vector<double> u0(joint_names_.size());ocp_nlp_out_get(nlp_config, nlp_dims, nlp_out, 0, "u", u0.data());for (size_t i = 0; i < joint_names_.size(); ++i) {effort_command =  u0[i]; // 計算關節力矩命令if (effort_command - last_torques_[i] > max_delta_[i]) effort_command = last_torques_[i] + max_delta_[i]; // 限制關節力命令的變化量else if (effort_command - last_torques_[i] < -max_delta_[i]) effort_command = last_torques_[i] - max_delta_[i]; // 限制關節力命令的變化量joint_effort_command_interfaces_[i].get().set_value(effort_command); // 設置關節力命令 }if (active_goal_ && reached_end){bool all_joints_reached = true;for (size_t i = 0; i < joint_names_.size(); ++i) {double pos_actual = joint_position_state_interfaces_[i].get().get_value();double pos_desired = point_interp_.positions[i];double error = std::abs(pos_actual - pos_desired);if (error > goal_tolerance_[i]) {all_joints_reached = false;break;}}if (all_joints_reached) {RCLCPP_INFO(get_node()->get_logger(), "All joints reached goal, sending SUCCEED to action server.");auto feedback = std::make_shared<control_msgs::action::FollowJointTrajectory::Feedback>();feedback->joint_names = joint_names_;feedback->desired = point_interp_;active_goal_->publish_feedback(feedback);auto result = std::make_shared<control_msgs::action::FollowJointTrajectory::Result>();result->error_code = control_msgs::action::FollowJointTrajectory::Result::SUCCESSFUL;active_goal_->succeed(result);trajectory_msg_.reset();active_goal_.reset();}}}else{// 沒有新目標，保持當前位置for (size_t i = 0; i < joint_names_.size(); ++i) {X_ref_[i] = point_interp_.positions[i]; // 獲取期望關節位置X_ref_[i + joint_names_.size()] = 0.0; // 獲取期望關節速度}X_ref_window_.clear();for (size_t k = 0; k < N_mpc_; ++k) {X_ref_window_.push_back(X_ref_);}Eigen::VectorXd xic = Eigen::VectorXd::Zero(joint_names_.size() * 2);for (size_t i = 0; i < joint_names_.size(); ++i) {xic[i] = joint_position_state_interfaces_[i].get().get_value(); // 獲取當前關節位置xic[i + joint_names_.size()] = joint_velocity_state_interfaces_[i].get().get_value(); // 獲取當前關節速度}// 調用MPC控制算法，計算關節力矩命令// 設置 x0// 只需要設置一次初始狀態約束（"lbx"/"ubx"）如果你的模型有 x0 約束ocp_nlp_constraints_model_set(nlp_config, nlp_dims, nlp_in, nlp_out, 0, "lbx", xic.data());ocp_nlp_constraints_model_set(nlp_config, nlp_dims, nlp_in, nlp_out, 0, "ubx", xic.data());for (int i = 0; i < X_ref_window_.size(); ++i) {ocp_nlp_cost_model_set(nlp_config, nlp_dims, nlp_in, i, "yref", X_ref_window_[i].data());}// 終端參考ocp_nlp_cost_model_set(nlp_config, nlp_dims, nlp_in, X_ref_window_.size(), "yref", X_ref_window_.back().data());int status = robot_nmpc_acados_solve(acados_ocp_capsule_);if (status != 0) {RCLCPP_WARN(get_node()->get_logger(), "acados solve failed: %d", status);}            // 求解std::vector<double> u0(joint_names_.size());ocp_nlp_out_get(nlp_config, nlp_dims, nlp_out, 0, "u", u0.data());RCLCPP_INFO_STREAM(get_node()->get_logger(), "u0: " << Eigen::Map<Eigen::VectorXd>(u0.data(), u0.size()).transpose());for (size_t i = 0; i < joint_names_.size(); ++i) {effort_command =  u0[i] ; // 計算關節力矩命令if (effort_command - last_torques_[i] > max_delta_[i]) effort_command = last_torques_[i] + max_delta_[i]; // 限制關節力命令的變化量else if (effort_command - last_torques_[i] < -max_delta_[i]) effort_command = last_torques_[i] - max_delta_[i]; // 限制關節力命令的變化量joint_effort_command_interfaces_[i].get().set_value(effort_command); // 設置關節力命令 }}// 發布當前力距命令effort_msg_pub_.header.stamp = time;effort_msg_pub_.name = joint_names_;effort_msg_pub_.effort.clear();for (const auto & interface : joint_effort_command_interfaces_) {effort_msg_pub_.effort.push_back(interface.get().get_value());}effort_command_publisher_->publish(effort_msg_pub_);// 發布當前軌跡指令trajectory_msg_pub_.header.stamp = time; // 正確：設置時間戳trajectory_msg_pub_.joint_names = joint_names_;trajectory_msg_pub_.points.clear(); // 清空舊點，避免累加trajectory_msg_pub_.points.push_back(point_interp_); // 正確：添加插值點joint_command_publisher_->publish(trajectory_msg_pub_); // 發布當前軌跡指令return controller_interface::return_type::OK; // 返回更新成功}