如何最簡單、通俗地理解線性回歸算法？線性回歸模型在非線性數據上擬合效果不佳，如何在保持模型簡單性的同時改進擬合能力？

線性回歸作為統計學與機器學習領域中最基礎且最重要的算法之一，其應用廣泛且深遠。它不僅是回歸分析的入門方法，更是后續復雜模型構建的重要理論基礎。理解線性回歸算法的本質，既有助于提升數據分析的能力，也能為掌握更復雜的機器學習算法打下堅實基礎。盡管線性回歸算法看似簡單，其背后蘊含的數學原理、統計假設以及實際應用的復雜性，卻值得深入探究。

線性回歸的核心思想是通過構建變量之間的線性關系模型，揭示自變量與因變量之間的關系規律，進而實現對未知數據的預測和解釋。這一方法基于經典的最小二乘估計思想，通過擬合樣本數據點，使模型預測值與真實值之間的誤差最小化。這里的“線性”不僅指變量間的關系形式，也體現為模型結構的簡單性，便于解析和計算。

在數據科學不斷發展、復雜算法層出不窮的時代，線性回歸依然具有不可替代的價值。它是理解參數估計、模型評估與假設檢驗的核心起點。透過線性回歸的框架，我們能夠系統地理解模型的可解釋性、泛化能力以及模型復雜度之間的權衡，這些都是構建穩健預測模型的重要議題。

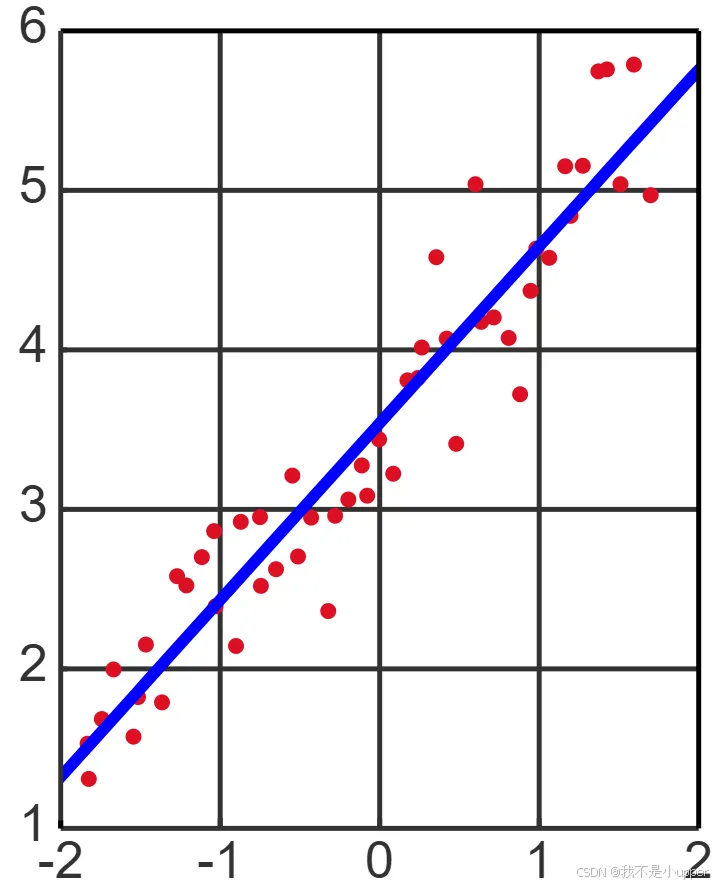
?線性回歸是一種用于刻畫因變量與自變量之間線性關聯的統計方法，其核心是通過數學模型量化這種關系。從形式上看，線性回歸的一般表達式為：

$y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_kx_k + \varepsilon$ ，

其中y為因變量， $x_1, x_2, \dots, x_k$ 為自變量， $\beta_0$ 是截距項， $\beta_1, \dots, \beta_k$ 是對應自變量的回歸系數（反映自變量對y的影響強度）， $\varepsilon$ 則為誤差項，代表模型無法解釋的隨機波動。建模的目標是找到最優參數 $\beta_0, \beta_1, \dots, \beta_k$ ，使得模型的預測值 $\hat{y} = \beta_0 + \beta_1x_1 + \dots + \beta_kx_k$ 盡可能接近真實觀測值y，這一過程通常通過最小二乘法實現 —— 即最小化平方殘差和：

$\sum_{i=1}^n (y_i - \hat{y}_i)^2$ 。

為保證模型的有效性與推斷合理性，線性回歸對誤差項$\varepsilon$有嚴格的統計假設：首先，誤差項的均值必須為零（ $E[\varepsilon] = 0$ ），確保模型預測無系統偏差；其次，誤差項需滿足同方差性（ $Var(\varepsilon) = \sigma^2$ ， $\sigma$ 為常數），即誤差的離散程度不隨自變量變化；同時，誤差項之間需相互獨立（ $Cov(\varepsilon_i, \varepsilon_j) = 0$ ， $i \neq j$ ），避免序列相關導致的估計偏誤；此外，誤差項需服從正態分布（ $\varepsilon \sim N(0, \sigma^2)$ ），這是后續假設檢驗與置信區間構造的基礎；最后，自變量之間不能存在完全線性相關（即無多重共線性），以保證參數估計的唯一性。這些假設是線性回歸推斷的理論基石，若被違反，可能導致參數估計偏差或模型解釋力下降，因此檢驗假設是否成立是分析過程的關鍵環節。

參數估計的核心是最小二乘法（OLS），從矩陣視角可更清晰推導其過程。設自變量矩陣為

$X = \begin{bmatrix} 1 & x_{11} & \dots & x_{1k} \\ 1 & x_{21} & \dots & x_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & \dots & x_{nk} \end{bmatrix}$ （第一列全為 1 對應截距項），

因變量向量為 $y = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}$ ，參數向量為 $\beta = \begin{bmatrix} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_k \end{bmatrix}$ ，則殘差平方和可表示為 $(y - X\beta)^T(y - X\beta)$ 。對 $\beta$ 求導并令導數為零，可得正規方程： $X^TX\beta = X^Ty$ ，若 $X^TX$ 可逆，則參數估計為 $\hat{\beta} = (X^TX)^{-1}X^Ty$ 。這一解析解具有無偏性、有效性等優良性質，若 $X^TX$ 不可逆（如存在多重共線性），則需通過奇異值分解（SVD）等數值方法求解。

模型訓練完成后，需通過性能指標評估擬合效果。殘差平方和（RSS）是基礎指標：

$RSS = \sum_{i=1}^n (y_i - \hat{y}_i)^2$ ，其值越小說明擬合越好；決定系數 $R^2$ 更直觀，公式為:

$R^2 = 1 - \frac{RSS}{TSS}$ （其中 $TSS = \sum_{i=1}^n (y_i - \bar{y})^2$ 為總平方和），反映模型解釋因變量變異的比例，取值范圍為 [0,1]，越接近 1 擬合越優；均方誤差（MSE） $\text{MSE} = \frac{1}{n}\sum_{i=1}^n (y_i - \hat{y}_i)^2$ 衡量平均預測誤差；均方根誤差（RMSE） $\text{RMSE} = \sqrt{\text{MSE}}$ 則將誤差轉換為與因變量同量綱的指標，便于實際解讀。實際應用中需結合多項指標綜合評估，避免單一指標的局限性。

線性回歸的適用存在一定限制：首先，它嚴格依賴因變量與自變量的線性關系，若實際關系為非線性（如二次、指數關系），模型擬合效果會顯著下降；其次，模型對異常值敏感，極端數據點可能大幅扭曲參數估計，影響預測穩定性；此外，自變量間的多重共線性會導致參數估計方差增大，使結果不穩定且難以解釋；最后，若誤差項的正態性或同方差性假設不滿足，傳統的 t 檢驗、F 檢驗等推斷結果可能失效。因此，數據預處理（如缺失值處理、異常值檢測）、變量篩選與假設檢驗是確保模型有效的必要步驟。

從數據到應用，線性回歸的實際流程可概括為：首先進行數據收集與清洗，確保數據質量（如處理缺失值、修正異常值）；其次是特征選擇與工程，篩選相關自變量，必要時進行歸一化、標準化或構造新特征（如交互項）；然后通過最小二乘法訓練模型，求解回歸系數；接著進行模型診斷，分析殘差分布以檢驗假設（如殘差是否正態、是否存在異方差）；之后計算 $R^2$ 、MSE 等指標評估性能；最后將模型應用于新數據進行預測。這一流程形成從理論到實踐的閉環，強調數據質量與統計假設對結果的決定性影響。

為防止過擬合、提升模型泛化能力，線性回歸常引入正則化方法，通過在目標函數中添加懲罰項約束參數復雜度。嶺回歸（L2 正則化）的目標函數為 $\sum_{i=1}^n (y_i - \hat{y}_i)^2 + \lambda\sum_{j=1}^k \beta_j^2$ （ $\lambda \geq$ ?0為懲罰強度），可減小參數估計的方差，尤其在多重共線性嚴重時效果顯著；Lasso 回歸（L1 正則化）則采用絕對值懲罰：

$\sum_{i=1}^n (y_i - \hat{y}_i)^2 + \lambda\sum_{j=1}^k |\beta_j|$ ，

能將部分參數壓縮至零，實現變量自動篩選，適合構建稀疏模型。兩種方法均通過調節 $\lambda$ 平衡偏差與方差，實際中需通過交叉驗證選擇最優懲罰參數。

線性回歸既是傳統統計學工具，也是機器學習中基礎的監督學習算法，二者雖形式相似但側重點不同：統計學視角強調模型假設、參數推斷（如通過 t 檢驗判斷系數顯著性），關注自變量對因變量的解釋機制；機器學習視角則更注重預測性能，強調模型在未知數據上的泛化能力，常結合正則化、梯度下降等優化手段處理大規模數據與高維特征。例如，當數據量極大時，傳統正規方程求解效率低下，此時迭代優化算法更適用 —— 梯度下降通過不斷沿目標函數負梯度方向更新參數 $\beta = \beta - \alpha\nabla J(\beta)$ ， $\alpha$ 為學習率， $J(\beta)$ 為損失函數）；隨機梯度下降（SGD）每次用單個樣本計算梯度，加快迭代速度；批量梯度下降（Batch GD）用全部數據計算梯度，收斂更穩定；小批量梯度下降（Mini-batch GD）則折中兩者，兼顧效率與穩定性，這些算法拓展了線性回歸在現代大數據場景中的適用性。

模型中自變量的選擇直接影響性能，常用方法包括：全子集回歸嘗試所有變量組合，選擇擬合最優者，但計算成本極高；逐步回歸通過前向選擇（從無變量開始逐步添加）、后向剔除（從全變量開始逐步移除）或雙向淘汰動態調整變量，平衡效率與效果；懲罰回歸（如 Lasso）則通過正則化自動實現變量篩選，適合高維數據。合理選擇變量可避免過擬合，提升模型的解釋力與泛化能力。

線性回歸的性能本質上受偏差與方差權衡影響：偏差是模型預測與真實值的系統偏離，方差是模型對訓練數據波動的敏感程度。線性回歸作為低復雜度模型，通常偏差較高、方差較低；增加模型復雜度（如引入高階項）可降低偏差但可能增大方差，而正則化則通過約束復雜度實現偏差與方差的平衡，最終提升泛化能力。

綜上，線性回歸融合了數學嚴謹性與應用實用性，其核心是通過線性模型刻畫變量關系，依賴嚴格的統計假設保證推斷有效性，借助最小二乘法與正則化等方法優化參數，并通過系統的評估與診斷確保模型穩健性。即便在復雜模型層出不窮的今天，線性回歸依然是數據分析的基礎工具，深入理解其原理與應用邊界，對構建科學的分析體系至關重要。